回弹法的测量不确定度评定
吴至复 满 银 方 瑶 周佳成
(1.国家电网有限公司,北京 100031;2.中国电力科学研究院有限公司,北京 100085;3.安徽绩溪抽水蓄能有限公司,绩溪 245300;4.同济大学地下建筑与工程系,上海 200092)
0 引言
测量的目的是为了确定被测量的量值,测量结果的品质是量度测量结果可信程度的最重要的依据。测量不确定度就是对测量结果质量的定量表征,测量结果的可用性很大程度上取决于其不确定度的大小。所以,测量结果表述必须同时包含赋予被测量的值及与该值相关的测量不确定度,才是完整并有意义的[1]。通俗地说,测量不确定度是指对测量结果可信性、有效性的怀疑程度或不肯定程度。由于测量不完善和人们认识的不足,所得的被测量值具有分散性,即每次测得的结果不是同一值,而是以一定的概率分散在某个区域内的多个值。虽然客观存在的系统误差是一个相对确定的值,但由于我们无法完全认知或掌握它,而只能认为它是以某种概率分布于某区域内的,且这种概率分布本身也具有分散性。测量不确定度可以反映测量结果分散性,由于认知不足,分散性更小的测量结果更容易被接受。
测量不确定度的标准定义为根据所获信息,表征赋予被测量值分散性的非负参数,此参数可以是标准测量不确定度的标准偏差(或其特定倍数),或是说明了包含概率的区间半宽度[2-3]。从定义上看,当测量结果确定时,测量不确定度也随之确定,而无须假设约定真值,因此比误差评定法更加具有可行性。
回弹法是检测混凝土强度最常用的方法,《回弹法检测混凝土抗压强度技术规程》(JGJ/T 23—2011)[4]指出,当测区数为10个及以上时,除了计算强度平均值还应计算强度标准差,这体现了测量不确定度的思想。但从整体上看,JGJ/T 23—2011[4]采用的推断方法并非是完全基于测量不确定度评定得到的。
为此,学者们对回弹法的测量不确定度进行了大量的研究。陈旭东等[5]、卜凡国[6]从混凝土、回弹仪使用条件、强度推断方法等角度分析了回弹法检测混凝土强度的不确定度来源;姚继涛和解耀魁[7]、马欣和王鑫晔[8]对回弹法测量误差的概率分布进行了研究,并基于此给出了不同于JGJ/T 23—2011[4]的强度推断方法,但需要指出的是,这并不是基于不确定度评定得到的;王建华和王琳[9]、何组钧和伦志强[10]认为回弹法测量不确定度主要来源于回弹值与碳化深度,并结合实例对回弹法的测量不确定度进行研究。
当前对回弹法不确定度的研究大多是基于特定的工程实例,而未形成系统的强度推断方法;虽有不同于JGJ/T 23—2011[4]的强度推断方法,但又不是基于不确定度评定得到的。为此,本文基于测量不确定评定基本原理,旨在提出回弹法的强度推断方法。
1 现行推断方法的缺陷
1.1 现行推断方法
JGJ/T 23—2011[4]中的推断方法是基于正态总体、总体标准差已知的前提下,对总体均值进行区间估计,以具有95%保证率的区间下限作为混凝土强度的推断值。
混凝土强度推断的方法以测区数10为界限,大致分为两类:
(1)测区数小于10

(2)测区数大于或等于10
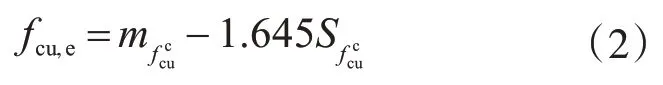
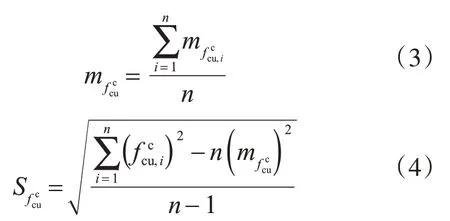
1.2 缺陷及解决措施
当测区数小于10时,按式(1)确定的混凝土强度推断值无法满足保证率为95%这一条件。陈旭东[11]分析了331组以最小值作为强度推断值的回弹法测试数据,得到有近70%构件强度推断值的保证率不足95%。究其原因,式(3)未考虑测量不确定度的影响,而仅利用了样本最小值来推断总体情况。根据数理统计基本原理,利用的样本数越少,则对总体的推断越不可信。
当测区数大于10时,由于式(4)给出的样本标准差并不是总体标准差的无偏估计,当测区数过少时,它自身也会产生较大的不确定度。根据数理统计基本原理,只有当n≥30时[7,11],才可利用式(2)进行推断,否则需要考虑式(4)引入的不确定度。
由于总体标准差未知,更加合理的方法是采用T分布进行区间估计,即
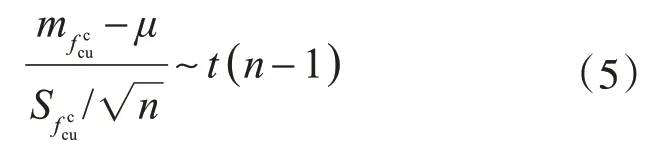
式中:μ为总体均值;t(n-1)为自由度是n-1的T分布;其余参数含义同前文。
根据数理统计基本原理,可得到具有95%保证率的混凝土强度推断值:
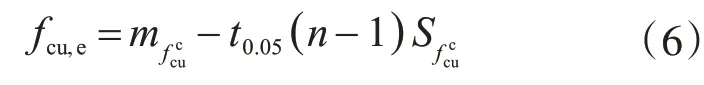
式中:t0.05(n-1)是分布t(n-1)置信度为0.05的分位值,可查表得到;其余参数含义同前文。
式(6)对测区数n的取值没有限制,但其仍未全面考虑测量不确定度的影响。当测区数越多,回弹仪性能越好,则强度推断值越可信,但式(6)无法体现这些因素对强度推断值的影响。
2 回弹法的测量不确定度
2.1 回弹法的数学模型
根据JGJ/T 23—2011[4],混凝土强度换算值与回弹值和碳化深度值有关。鉴于目前尚无公认的强度换算值与回弹值、碳化深度的理论公式,因此在建立数学模型时只能采用无显式表达式的透明箱模型,即

式中:fcu为混凝土强度换算值;分别是第i测区的回弹值均值与碳化深度均值;f(·)为由回弹值与碳化深度值换算成混凝土强度的函数,可根据测强曲线换算。
2.2 测量不确定度的来源
由式(7)可知,混凝土强度换算值的不确定度与回弹值、碳化深度值的不确定度有关。
2.2.1 回弹值的不确定度
回弹值的影响量有很多,有些影响量的不确定度尚未研究成熟,如混凝土强度空间变异性的不确定度,这类影响量的不确定度无法考虑;有些影响量的不确定度较小,如回弹仪与上次校准结果的微小偏差引入的不确定度,这类影响量的不确定度无须考虑。结合以往的研究成果[5-6,9-10],回弹值不确定度的来源如下。
1.测量重复性引入的不确定度u1R
重复测量会引入不确定度,它往往是由测量过程中的随机效应导致的。对于此类不确定度,采用A类评定的贝塞尔公式法进行计算。
合并样本标准差按下式计算
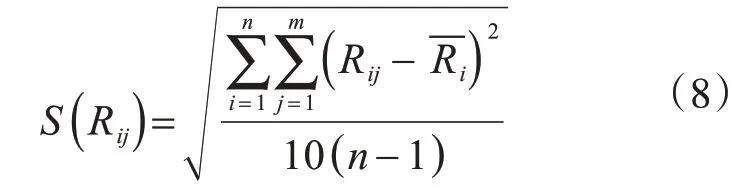
式中:Rij是第i测区第j个测点的回弹值,该值指去除3个最大值和3个最小值之后的10个回弹值;S(Rij)为回弹值的合并样本标准差;其余参数含义同前文。
各测区的回弹值是以平均值为代表值,故测量重复性引入的不确定度u1R为
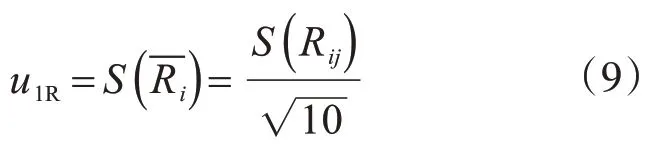
2.读数误差引入的不确定度u2R
对于指针式示读回弹仪,测量人员的读数误差在±0.5分度值之内,且在该区间内服从均匀分布。按照B类评定方法得

式中,各参数含义同前文。
对于数显式回弹仪,读数误差源于最小刻度的修约间隔δ1,由此引入的不确定为

式中,各参数含义同前文。
3.弹击角度倾斜引入的不确定度u3R
根据工程经验,由于弹击角度倾斜导致的误差在±1分度值之内,且在该区间内服从均匀分布。按照B类评定方法得

式中,各参数含义同前文。
4.系统性能引入的不确定度u4R
回弹仪系统性能引入的示值误差±e1应参考相应的检定证书。示值误差在±e1之内服从均匀分布,按照B类评定方法得

式中,各参数含义同前文。
5.对非水平方向检测、水平方向检测非浇筑侧面修正引入的不确定度u5R
根据JJF 1059.1—2012[3],当对已知的系统误差进行修正时,需要考虑修正值引入的不确定度。当回弹仪为非水平方向时,应进行角度修正,修正值的误差±e2根据工程经验确定,且服从均匀分布,按照B类评定方法得

式中,各参数含义同前文。
当回弹仪为水平方向但测区非浇筑侧面时,也应进行相应的修正。修正值的误差±e3根据工程经验确定,且服从均匀分布,按照B类评定方法得

式中,各参数含义同前文。
当回弹仪为非水平方向且测区为非浇筑侧面时,由方差传递原理
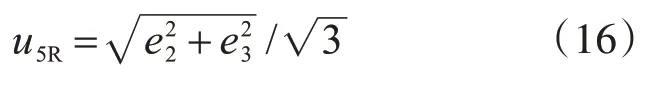
式中,各参数含义同前文。
2.2.2 碳化深度的不确定度
和回弹值一样,考虑目前已经掌握的碳化深度影响量的不确定度。
1.测量重复性引入的不确定度u1d
当代表性测区碳化深度极差不大于2 mm时,以该测区的碳化深度均值作为所有测区的碳化深度值,此时由碳化深度引入的不确定度可由A类评定的贝塞尔公式得到
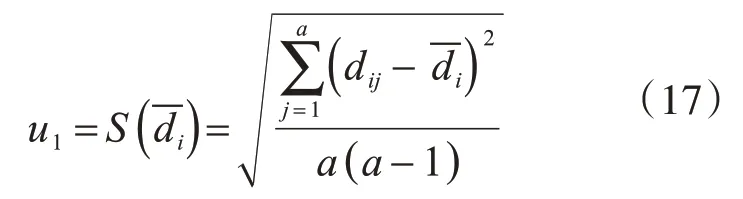
当代表性测区碳化深度极差大于2 mm时,需要对每个测区的碳化深度都进行测量,此时应采用合并标准差评定测量不确定度,即
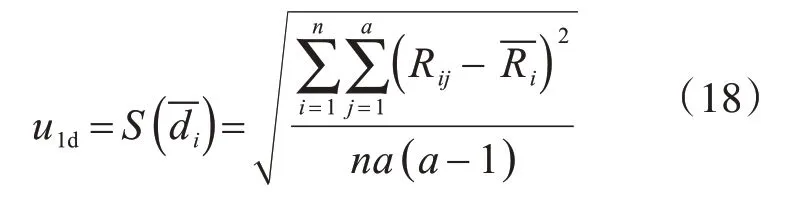
式中,各参数含义同前文。
2.读数误差引入的不确定度u2d
碳化深度的测量常用游标卡尺或数显式碳化深度测定仪测定,按照B类评定方法得

式中:δ2为碳化深度测定仪的修约间隔,按检定证书确定;其余参数含义同前文。
3.系统性能引入的不确定度u3d
游标卡尺或数显式碳化深度仪引入的示值误差±e4应参考相应的检定证书,并按照B类方法进行评定

式中,各参数含义同前文。
将上述回弹值与碳化深度影响量的不确定度总结见表1。

表1 回弹法不确定度评定Table 1 Evaluation for uncertainty of rebound method
2.3 回弹法的合成标准不确定度
虽然3.2节分析了回弹值与碳化深度不确定度的来源,但却无法定性描述各来源是如何影响测量结果的,因此它们之间的关系只能用黑箱模型描述。对于黑箱模型,灵敏系数为1。
各来源的标准不确定度不相关,根据方差传递原理,得
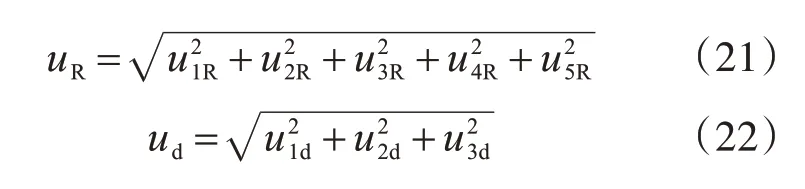
式中:uR、ud分别为回弹值、碳化深度的合成标准不确定度;其余参数含义同前文。
由于式(7)没有显式表达式,假设它是线性的,得强度换算值的合成标准不确定为
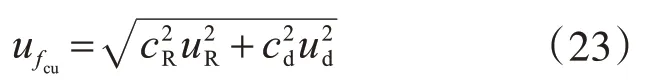
式中:ufcu为混凝土强度换算值的不确定度;cR,cd为灵敏系数,由式(7)的数学模型按式(23)确定;其余参数含义同前文。
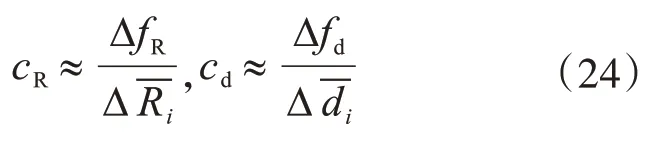
得到合成标准不确定度之后,可按下式计算强度推断值。
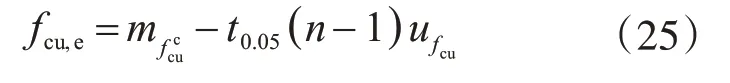
式中,各参数含义同前文。
3 算例
佛山市某废弃工业厂房改建工程,混凝土框架结构,C25泵送混凝土。该厂房由于长时间废弃,且原施工方养护不到位,混凝土强度无法保证。为确定合理的改造加固方案,对该厂房框架梁、柱进行回弹法检测抗压强度,以推定目前混凝土的实际强度。
利用指针式回弹仪对该厂房某框架梁浇筑侧面进行水平方向测量,测区数为10,各测区回弹值均值、碳化深度均值、强度换算值见表2。回弹仪系统性能引入的示值误差为±1.5分度值。采用游标卡尺测量碳化深度,游标卡尺系统性能引入的示值误差为±0.01分度值。
结合表1,得到算例的回弹值、碳化深度不确定度计算结果,见表3。
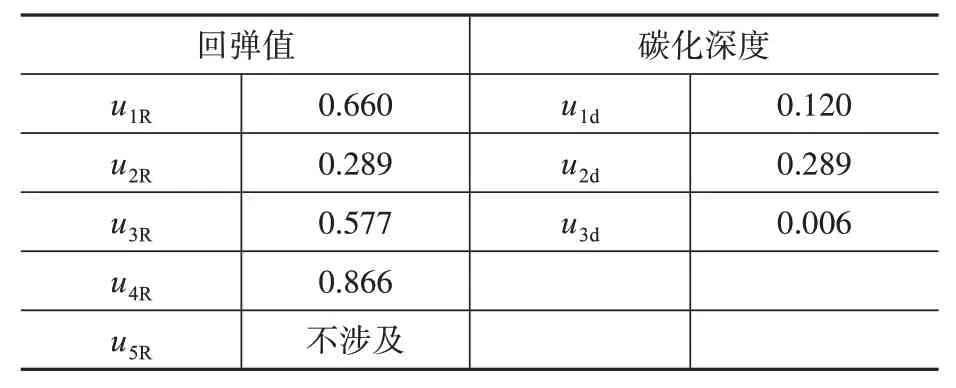
表3 不确定度计算结果Table 3 Uncertainty calculation results
由式(24)计算灵敏系数,取增量分别为0.2和0.5 mm,得cR=1,cd=2.2。由式(21)至式(23)得合成标准不确定度
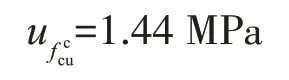
由表2得强度换算值的均值及标准差。
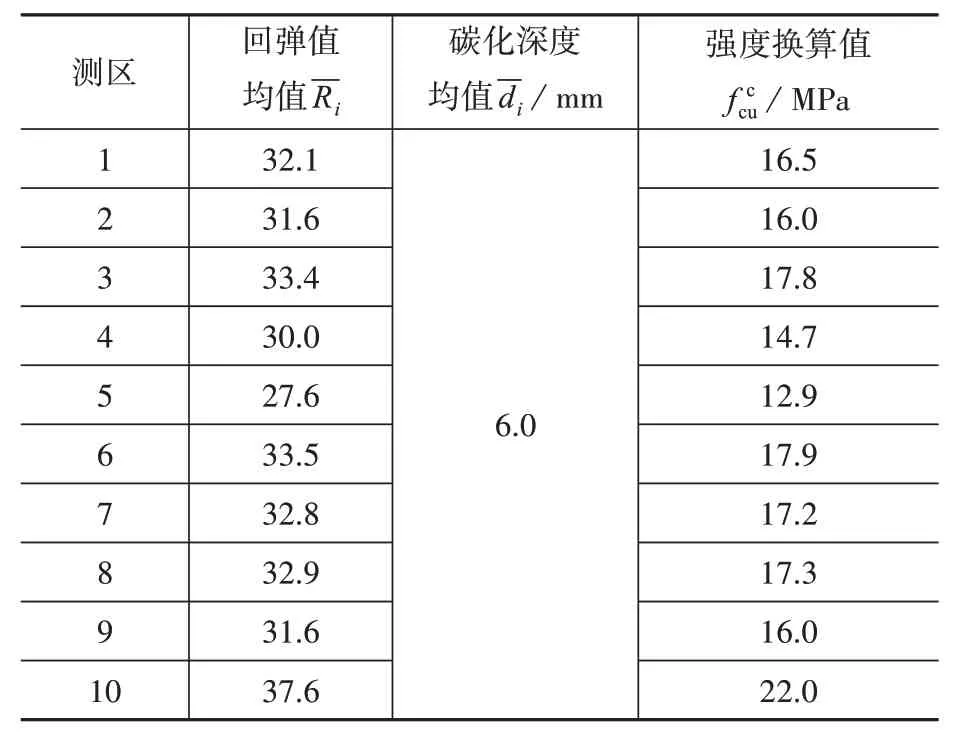
表2 各测区测量值与换算值Table 2 Measured value and conversion value of each survey area
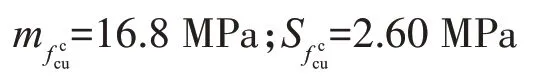
按JGJ/T 23—2011[4]的推断方法,得强度推断值为12.5 MPa,该值具有95%的保证率;考虑测量不确定度的强度推断值为14.2 MPa,该值为具有95%保证率的单侧置信区间的下限。后者的推断值比前者大,且保证率比前者也高,这看似是矛盾的。要解释这个问题,需从两个角度考虑。
其一,根据数理统计及测量不确定评定基本原理,保证率与推断值的大小无关,而与认知程度及不确定度大小有关。例如,用两把准确度不同的直尺去测量某个物块的长度,物块长度真值为1 mm。准确度差的直尺测量结果为1 mm,准确度好的直尺测量结果为1.1 mm,这在概率上是可能发生的事情。从测量结果上看,即使前者的测量结果更接近真值,但由于我们事先并不知晓真值大小,只能根据测量不确定度(准确度)差异,选择后者的测量结果作为物块的长度代表值。
其二,考虑到回弹法是按照分测区测量、以各测区均值作为代表值的特点,采用式(8)、式(9)的合并标准差及均值标准差比式(4)的标准差更加合理。对比发现,式(8)、式(9)的分母要大于式(4),因此由测量重复性引入的不确定度小于式(4)的计算值。
4 结论
测量结果需包含被测量的值及相应的测量不确定度,才是完整并有意义的。本文基于测量不确定度基本原理,假设混凝土强度推定值与回弹值、碳化深度值的关系是线性的,分析了回弹法测量不确定度的来源并给出相应的表示方法,最终给出了回弹法测量不确定度的理论表达式。
本文方法具有以下两点优势:其一,本文方法对样本容量无限制要求,这是由于本文方法在计算不确定度时已考虑样本容量的影响;其二,不论样本容量大小,本文得到的强度推断值的保证率均为95%。传统方法采用正态分布描述抽样分布,当样本容量较大时,其与实际分布(t分布)的差异较小;但当样本容量较小时,其与实际分布(t分布)的差异较大。本文的方法是基于t分布得到,所以不存在此问题。

