基于图像处理20钢的晶界提取算法

韩越祥， 卢振发

（1.浙江工业职业技术学院设计与艺术学院，浙江绍兴315100；2.江苏大学材料科学与工程学院，江苏镇江212013）

0 引 言

具有铁素体＋珠光体组织特征的钢材在我国工程结构材料中应用广泛，这主要与其加工成本较低、强塑性较好等有关，在对铁素体＋珠光体钢材进行组织分析时，如何有效地进行晶界提取是广大科研工作者长期关注的课题［1］，然而，实际应用过程中还没有专用的金相设备或者晶界提取算法能够处理所有类型的金相组织。近些年来，虽然在晶界提取算法上发展了一些新的理论并提出了新的算法，但是由于晶界提取过程较为复杂（图像预处理与分割、阈值设定、子图像处理等）、影响因素较多［2］，常用的基于形态学的Kirsch算子、Roberts算子、Canny算子、LoG算子和Soble算子等在处理图像时还无法提取到完整的晶界，最终图像处理结果中的晶界也往往会受到噪声点多、图像分割等的影响［3-5］。本文选取具有代表性的组织类型为铁素体＋珠光体的20钢为研究对象，通过对金相组织进行预处理与分割、子图像处理、晶界提取和晶界优化等步骤［6］，提出了适宜于20钢的基于Kirsch算子的自适应多阈值晶界提取算法，并对其进行了滞后阈值优化处理，结果将有助于快速、准确的晶界提取和定量分析，改善金相定量评级效率低、准确度差等问题，更好地满足大批量金相组织检测需求。

1 材料与图像处理方法

实验材料为江苏沙钢集团生产的热轧20钢板，组织类型为铁素体＋珠光体。基于图像处理的晶界提取算法流程主要包括：输入图像、预处理与分割、子图像分类、设置阈值、晶界提取、晶界优化和输出晶界等。其中，对输入的图像进行预处理与分割是晶界提取算法的前提，这主要是因为金相组织通常是由不同类型和尺寸的晶粒组成，晶界提取前需要区分不同噪声点和不同清晰度的晶界，以增加后续晶界提取的辨识度［7］；在对输入图像进行预处理与分割后，不同面积大小和信息熵的子图像因有各自不同的特点而需要采用不同的晶界提取算法［8］，因此需要进行子图像分类；子图像分类处理后需要进行阈值设定，这是因为子图像中的像素点和噪声等会对晶界提取产生影响，而阈值设定可以降低对噪声的敏感度以及提升图像处理效果［9］，本文基于Kirsch算子的晶界提取算法设定的阈值介于20～45；如果设置单个阈值进行晶界提取会出现阈值与图像信息不匹配的问题，因此采用经过预处理与分割的改进分水岭算法和k均值聚类算法与Kirsch算子相结合来对晶界进行提取；对于噪声点较多、图像质量较差的金相组织，进一步采用滞后阈值算法进行晶界优化，即对图像设定一个较高阈值和一个较低阈值，并以较低阈值的结果作为真实边缘，以降低噪声等的干扰。

2 结果及讨论

2.1 图像预处理与分割

采用改进分水岭算法［10］对20钢的金相组织进行预处理与分割，改进分水岭算法处理图如图1所示，包括预处理后的金相图像和经过改进分水岭算法处理后的效果图。对比分析可知，对于晶粒完整且尺寸较大、噪声点较少的晶粒，改进分水岭算法可以实现良好分割，如图1中方框所示；而对于晶粒不完整、腐蚀效果较差以及噪声点较多的晶粒，改进分水岭算法并不能完全消除噪声点干扰，但是可以做到减弱干扰的效果，如图1中圆框所示。

图1 改进分水岭算法处理图

采用k-均值聚类算法［11］对20钢的金相组织进行预处理与分割，k-均值聚类算法处理图如图2所示，包括以5个聚类中心和以2个聚类中心进行聚类操作的图像。对比分析可知，以5个聚类中心进行k均值聚类算法处理的图像在圆框所示区域的聚类效果较好，该区域像素灰度基本一致，有助于后续晶界提取，而对于方框所示区域的聚类效果较差，该区域像素灰度不稳定，会在一定程度上影响后期晶界提取效果。当以2个聚类中心进行k-均值聚类算法处理图像，则会由于铁素体的灰度值较小（远低于附近像素点和晶界区域像素点）而使得金相组织图像中只能提取到铁素体信息，而忽略了晶界信息，见图2（b）。

图2 k均值聚类算法处理图像

2.2 子图像分类

采用上述改进分水岭算法对20钢的金相组织进行预处理与分割后，输入的图像都会转化成n个子图像。其中，面积较大的子图像和面积较小的子图像由于噪声点多少不同而适应于不同阈值提取，当采用改进分水岭算法提取面积较大的晶粒区域时，较小的阈值即可完成准确识别，而对于面积较小、噪声点较多的区域，需要采用较大的阈值才能去除伪晶界的影响以提高识别率［12］。

对图1中的子图像进行面积统计分析，结果如图3所示，图3（a）的子图像面积曲线图中面积较小且数量最多的区域对应曲线中缓慢上升阶段（像素面积＜1 000），采用改进分水岭算法并不能完全解决噪声多区域的分割问题；子图像面积曲线图中平稳上升阶段（像素面积介于1 000～4 000）则对应于图1中有部分噪声的区域，此时的改进分水岭算法可以一定程度上解决分割问题，但是还不能实现100%消除噪声影响，后期采用严格的标准可以较好地实现晶界的提取；子图像面积曲线图中快速上升阶段（像素面积＞4 000）则对应于图1中晶粒完好的区域，此时的改进分水岭算法基本可以解决晶界提取问题。由图3（b）可见，像素在不同阶段都呈现梯度分布特征，即在实际晶界提取过程中，对子图像设置不同的晶界提取标准就可以得到识别率较高的晶界。

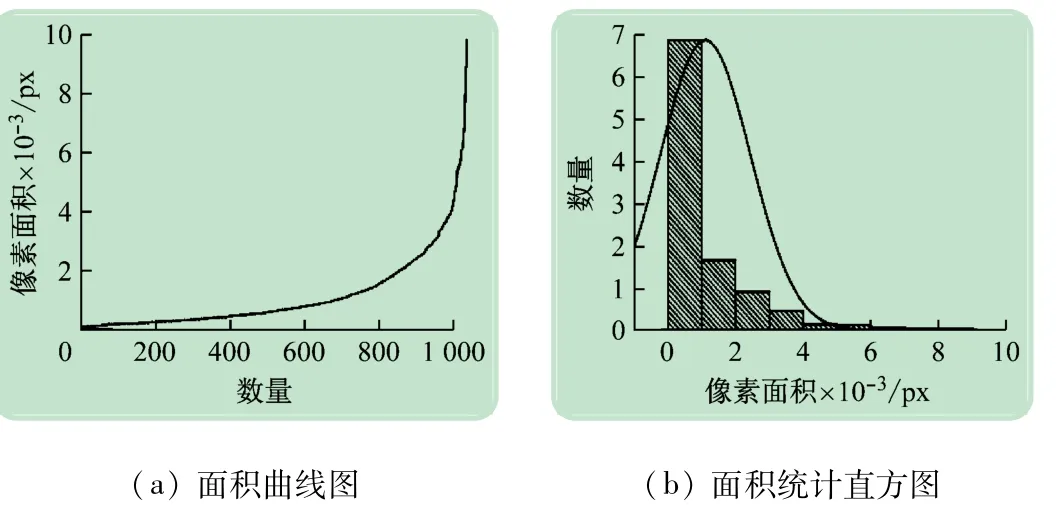
图3 改进分水岭算法处理后子图像面积统计图

以图2（a）为例进行k-均值聚类算法处理，图4为k-均值聚类算法处理后子图像面积统计图，其中，右上角1、63、127、191和255分别为5个聚类中心的灰度阶数［13］。由于此时的子图像类别不如采用改进分水岭算法处理子图像时那么多，且这5个子图像的面积差异较小，因此，单从面积大小上无法区别图像中不同区域应该采用哪种晶界提取算法来进行，需要进一步研究不适宜区域面积法的分类算法［14］。

图4 k-均值聚类算法处理后子图像面积统计图

采用区域面积法进行经过图像预处理与分割的子图像的晶界提取时存在一定缺陷，因此，进一步使用了图像信息熵（表征图像信息的丰富度）的方法对子图像进行了分类处理，这种方法可以区分子图像中不同区域的噪声里多少以及图像复杂程度等［15］。图5为采用改进分水岭算法和k-均值聚类算法处理后子图像的信息熵统计图，其中，信息熵越大则表示子图像中灰度变化多且快，而相同灰度区域的信息熵为0。对比分析可知，采用改进分水岭算法处理后，子图像的信息熵统计图可分为快速增长阶段（该区域噪声点少、灰度值较为接近，适宜于宽松的晶界提取算法）、快速减缓阶段（该区域噪声点增多、灰度值有一定差异，适宜于较严格的晶界提取算法）和平稳上升阶段（该区域噪声点多、灰度值变化剧烈，适宜于严格的晶界提取算法）［16］。采用k-均值聚类算法处理后，子图像的信息熵统计图如图5（b）所示，其中1、2、3、4和5分别表示灰度阶数为1、63、127、191和255的子图像。可见，3和4属于高信息熵；2和5属于中信息熵；1属于低信息熵，而信息熵越高则子图像中噪声点越多，越需要更严格的晶界提取算法。经过改进分水岭算法和k-均值聚类算法处理后子图像的信息熵分类效果图见图6。

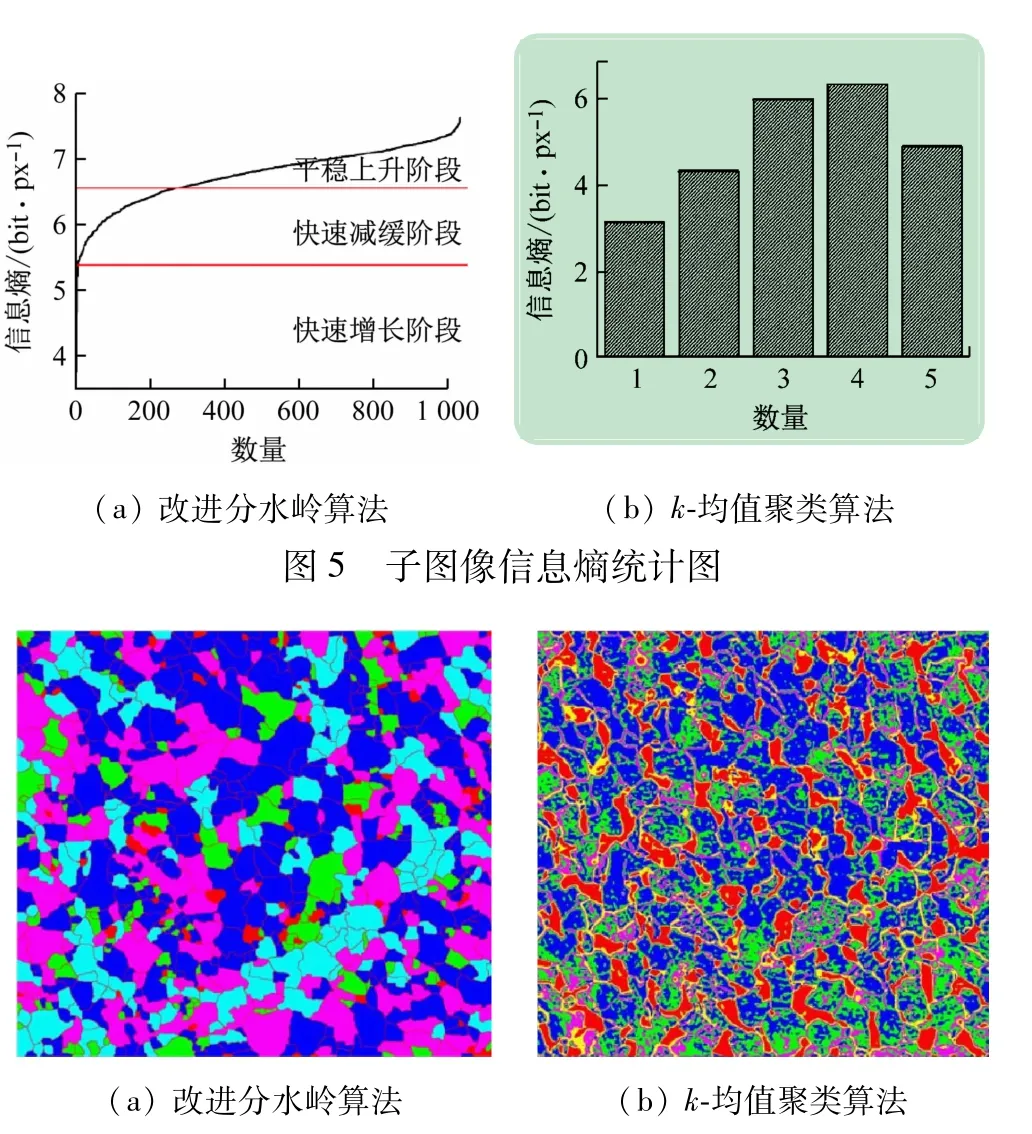
图6 不同算法处理后子图像信息熵效果图

2.3 晶界提取

通过上述子图像分类处理结果可知，实际应用过程中不同子图像需要采用不同的晶界提取算法。图7为基于Kirsch算子［17］的晶界提取效果图，其中，子图像对噪声的敏感度通过阈值T来表征，T介于20～45。对比图7的不同阈值条件下晶界提取效果图可知，T较小时对应的晶界提取效果图中的噪声干扰较多，反映出来的晶界数量明显多于T较大（噪声干扰较小）时的晶界提取效果图，因此，对于含有不同噪声点的图像，如何选择合适的阈值来获取晶界提取效果较好的图像则尤为重要。

进一步将改进分水岭算法和k-均值聚类算法与Kirsch算子相结合得到的自适应多阈值晶界提取效果图如图8所示，其中T都选取为30－20－20－25－35。可见，改进分水岭算法＋Kirsch算子和k均值聚类算法＋Kirsch算子的自适应多阈值晶界提取效果图都要优于图7的基于Kirsch算子的晶界提取效果图。对于图8（a）所示的改进分水岭算法＋Kirsch算子得到的效果图，方框中噪声点要相对单阈值为20的晶界提取结果少（图7（a）），且要相对单阈值为40的晶界提取得到的晶界更完整（图7（e）），即采用自适应多阈值晶界提取方法可以避免由于噪声多而影响晶界提取效果。对于图8（b）所示的k-均值聚类算法＋Kirsch算子得到的效果图，方框中的晶界提取效果与图8（a）相似，但是圆框中的噪声点要少于图8（a），即相对具有更佳的晶界提取效果。

图7 不同阈值条件下晶界提取效果图

图8 自适应多阈值晶界提取效果图

2.4 晶界优化

虽然采用改进分水岭算法＋Kirsch算子和k-均值聚类算法＋Kirsch算子的自适应多阈值晶界提取效果图要明显优于采用单一阈值的晶界提取效果图，但是图8中仍然存在较多的噪声点，因此，有必要采用滞后阈值的方法［18］来对晶界进行进一步优化，即在图像处理时分别设定一个较高的阈值和一个较低的阈值对图像边缘进行提取，并以相应处理结果作为存疑边缘和真实边缘，然后以设定算法遍历边缘，以确定图像中的点是噪声点还是晶界点。采用滞后阈值算法对图8（b）进行晶间优化处理后的图像如图9所示。对比可知，滞后阈值算法处理后的图像中的噪声点相对处理前有所减少，但是晶界却没有受到影响，即晶界提取效果进一步增强。

图9 滞后阈值算法进行晶间优化处理后的图像

图10为手工提取得到的20钢的晶界效果图和晶界二值图。由图10可见，20钢的晶界非常清晰，可以作为20钢的晶界提取标准，设定此时的晶界匹配率为100%，晶界二值图中可知，此时20钢的晶粒个数和平均面积分别为259和4 317.2 μm2，手工提取晶界的方法耗时3 600 s。不同阈值条件下基于Kirsch算子的晶界提取效果和本文提出的滞后阈值算法（ZIPC）的晶界提取效果进行对比分析，结果见表1。可见，基于Kirsch算子得到的晶界提取效果图中的晶粒个数和晶粒平均面积会由于单阈值的不同而存在较大差异，而运行时间不变且都明显低于手工提取方法；当阈值T从20增加至40时，晶粒个数在343～168之间变化，晶粒平均面积在（3 257.1～6 679.0）μm2。未经预处理的ZIPC算法和经过预处理的ZIPC算法的运行时间分别为18和20 s，明显低于手工提取方法，且相应的晶粒个数分别为272和238，相应的晶粒平均面积分别为5 380.5和4 169.0 μm2。对比表1的晶间提取效果统计结果可知，本文提出的经过预处理的滞后阈值算法的晶界提取时间较短，且与手工提取方法得到的晶粒个数和晶粒平均面积最为接近。

图10 手工提取法得到的20钢的晶界

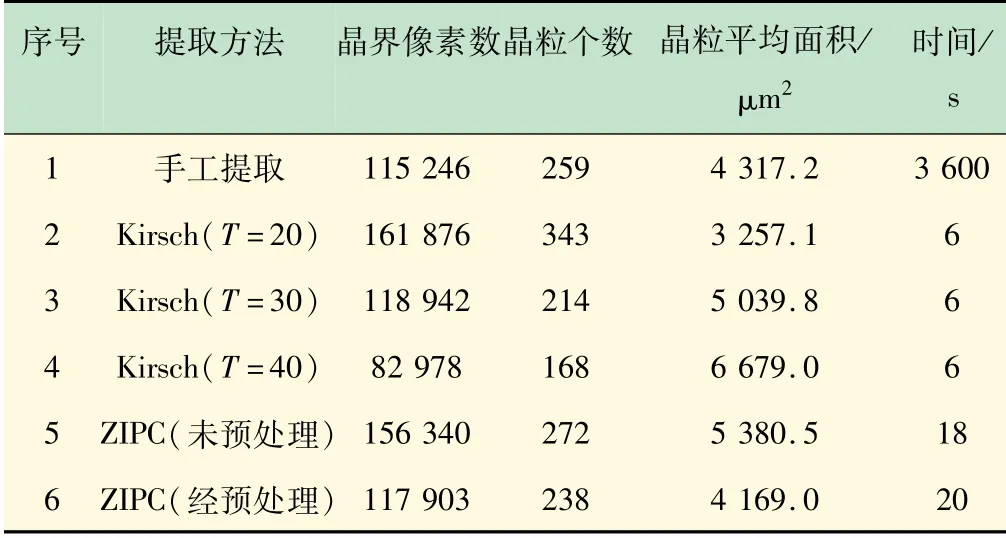
表1 不同算法下晶界提取的对比结果

3 结 论

（1）对于晶粒完整且尺寸较大、噪声点较少的晶粒，改进分水岭算法可实现良好分割，而对于晶粒不完整、腐蚀效果较差以及噪声点较多的晶粒，改进分水岭算法并不能完全消除噪声点干扰。当采用改进分水岭算法提取面积较大的晶粒区域，较小阈值即可完成准确识别，而对于面积较小、噪声点较多区域，需要采用较大的阈值才能去除伪晶界的影响以提高识别率。

（2）改进分水岭算法＋Kirsch算子和k-均值聚类算法＋Kirsch算子的自适应多阈值晶界提取效果图都要优于基于Kirsch算子的晶界提取效果图。

（3）基于Kirsch算子得到的晶界提取效果图中的晶粒个数和晶粒平均面积会由于单阈值的不同而存在较大差异，而运行时间不变且都明显低于手工提取方法；当阈值T从20增加至40时，晶粒个数在343～168之间变化，晶粒平均面积在3 257.1～6 679.0 μm2。未经预处理的ZIPC算法和经过预处理的ZIPC算法的运行时间分别为18和20 s，明显低于手工提取方法，且相应的晶粒个数分别为272和238，相应的晶粒平均面积分别为5 380.5和4 169.0 μm2。