基于Matlab的测量平差程序设计与实现
杨宏斌,孟福军,岳胜如
(塔里木大学水利与建筑工程学院,新疆 阿拉尔 843300)
工程应用中,大量测量数据处理需要繁重的计算过程。人工计算效率低下,费时费力,非常影响工程进度[1-2]。Matlab可以集中进行科学计算,结果可视化,功能强,使用方便,易于掌握[3-4],可以非常容易地解决繁杂的数据计算,还能进行用户界面(GUI)图形设计[5-6]。在Matlab基础上进行控制测量平差程序设计,便于建立平差模型、解算数据和图形展示。史建青等[3,6-7]基于MATLAB,设计了导线网平差程序;高霞等[4-5,8]提出基于Matlab的高程控制网平差;石丽梅等[9-10]运用C++语言实现导线网间接平差近似坐标计算。在上述研究成果基础上,实现平面控制网和高程控制网平差程序设计,把程序整合成为软件,帮助完成数值计算和数据处理等任务,通过实例进行验证分析,实践表明,该软件切实可行,在一定程度上降低了测绘人员的计算工作量。
1 平差程序设计
1.1 平面控制测量平差程序设计
设计流程如图1所示。读取野外测量数据,包括角度数边长数据。对已知点及待求点进行编号,分别给角度和距离观测值编点号,形成角度观测值矩阵和边长观测值矩阵。计算待测点位置的近似值,组成矩阵。定权并组建误差方程式,按照间接平差理论进行平差计算,输出平差结果。

图1 平面测量平差程序设计流程图
1.2 高程控制测量Matlab平差程序设计
设计流程如图2所示。由于高程测量控制网列立间接平差误差方程式具有很强的规律性,便于进行计算机语言编写,故程序选用间接平差原理。将点号、观测高差、路线长度和已知高程数据输入到数据库文件中,按间接平差方法,选待定高程点作为平差的未知参数,根据已知高程点和观测路线高差,求出各待测点高程近似值,由高程近似值和水准路线高差观测数据,求出每条水准路线中常数项,再根据观测路线列水准网的误差方程,形成系数矩阵,有了系数矩阵和常数项,便可建立误差方程。由误差方程组成法方程,通过解法方程,求取未知参数并计算中误差,从而进行精度分析,导出结果报告。
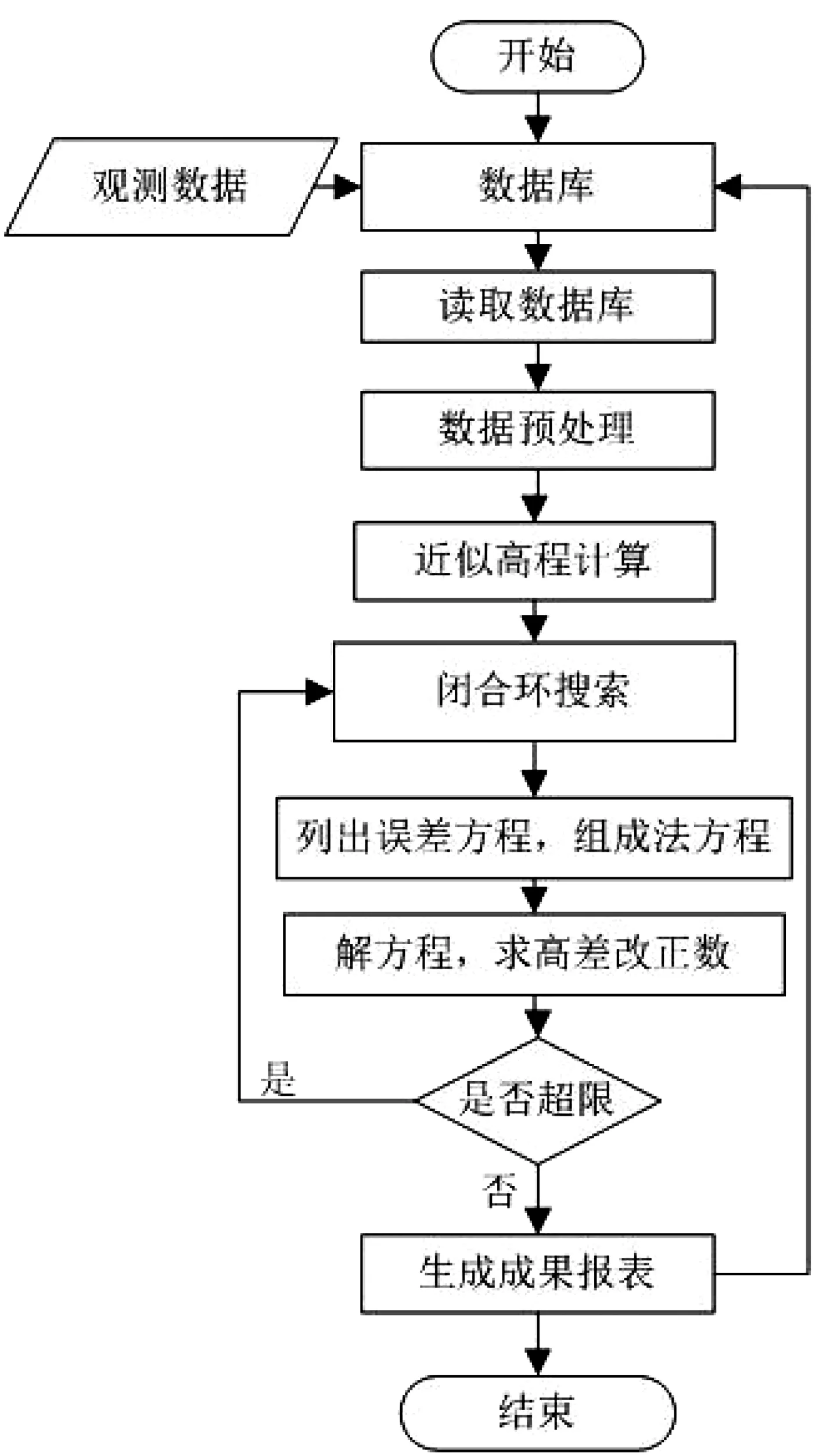
图2 高程测量平差程序设计流程图
2 测量平差程序设计的应用实例
2.1 程序主界面
主界面如图3所示。下拉菜单有两个选项,选择其中一个,就可弹出高程网或平面网平差解算界面。

图3 程序主界面
2.2 实例分析
2.2.1 导线平差计算
导线网平差过程主要包括:角度闭合差的计算与调整、坐标方位角推算、坐标增量计算、坐标增量闭合差的计算与调整、导线坐标点的计算。将已知数据和观测值(距离和角度)输入到Excel中,如图4所示。单击“读取数据”,选择已编辑好的数据,再点击“开始平差”,即可计算出待求坐标及图形显示,并通过“生成报表”来导出平差成果,如图5所示。

图4 附合导线已知点坐标和观测数据

图5 导线平差成果
2.2.2 MATLAB在高程控制网平差中的实例应用
图6为高程控制网数据处理界面,图7为保存在Excel表中水准测量数据,其中包括已知高程点数据及待计算高程点个数。点击“读取数据”按钮,Excel中的水准数据就会在程序界面的控件中展示出来,选择“开始平差”,便可计算高差闭合差、线路总长及单位权中误差。点击“生成报表”按钮,得出结果(表1所示)。
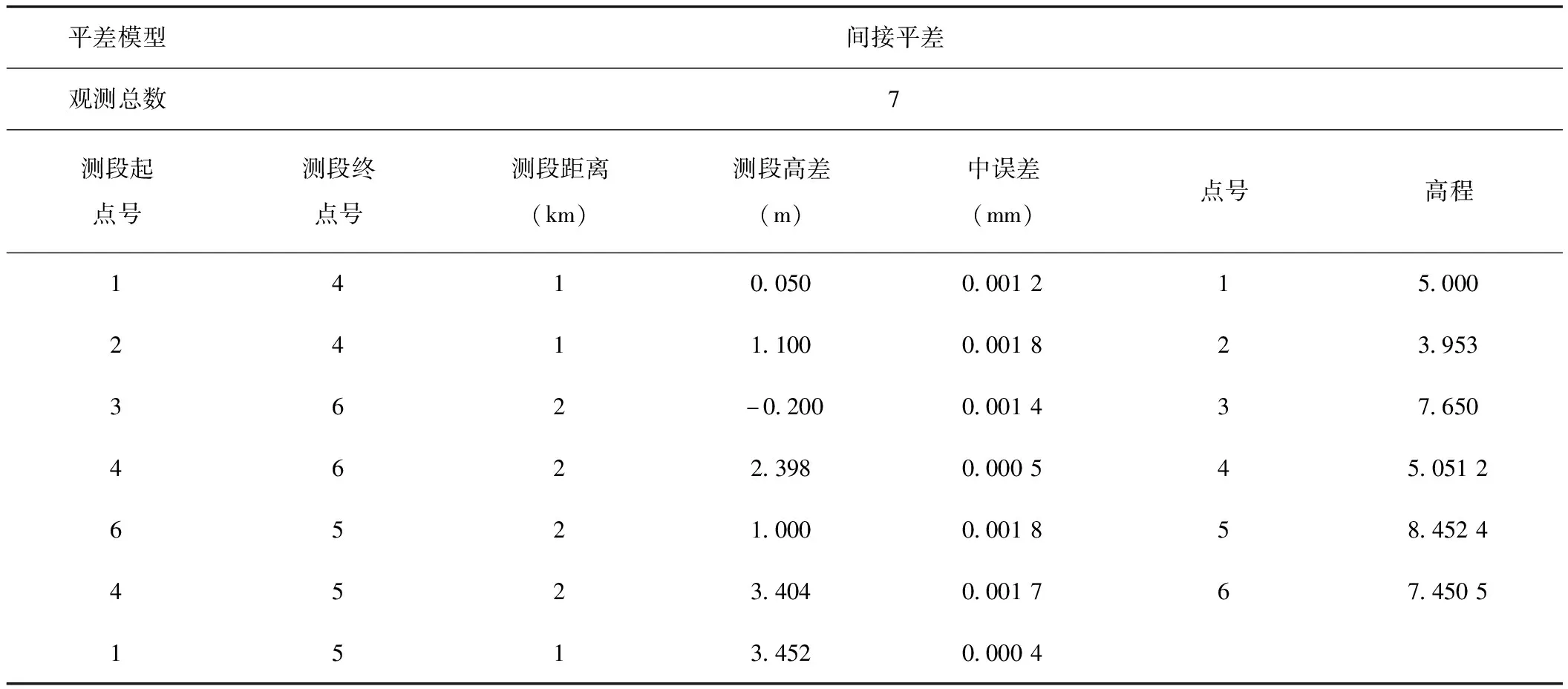
表1 平差报表输出结果

图6 水准测量数据处理界面
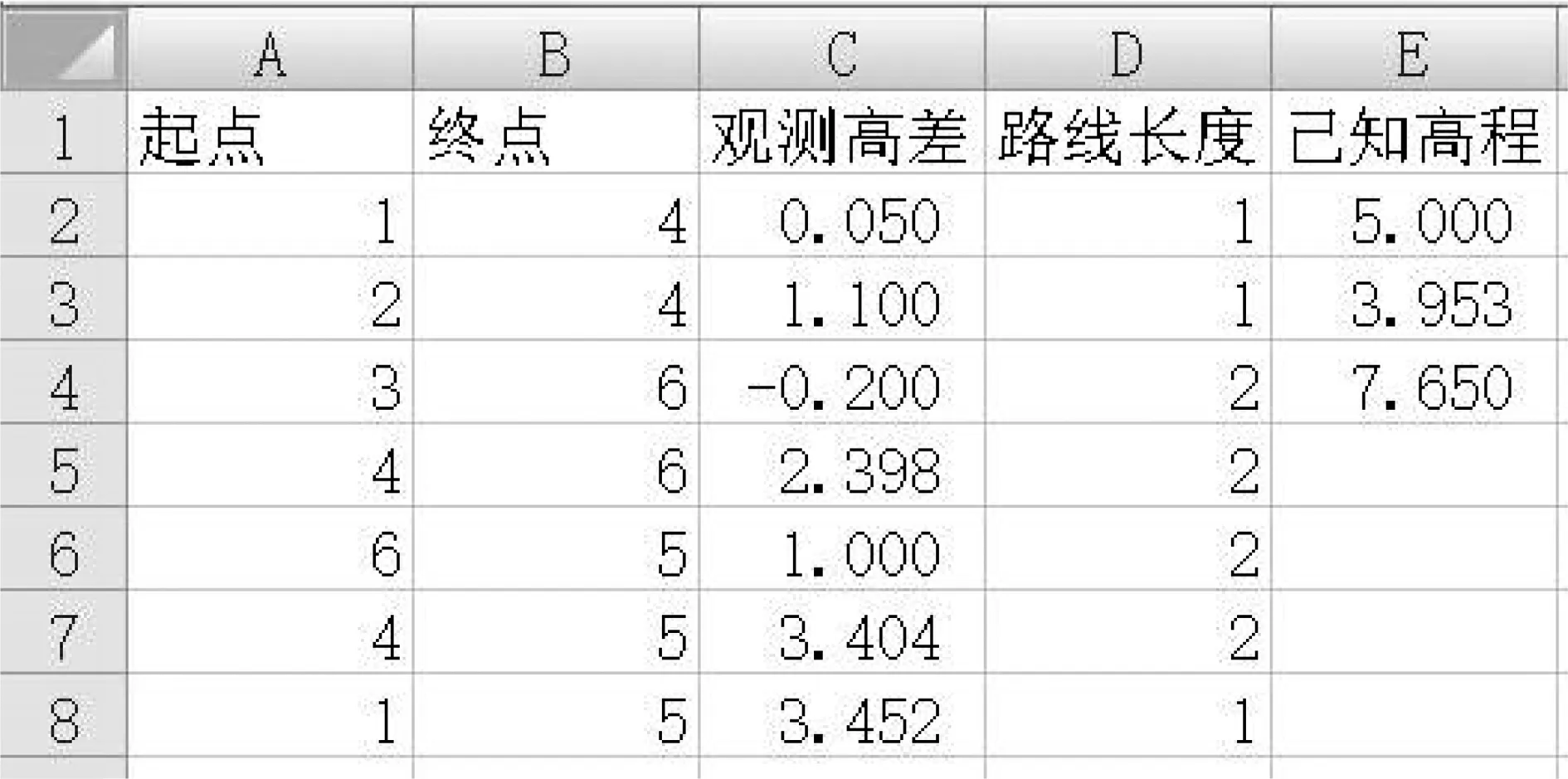
图7 已知数据和观测数据
3 结论
设计了平面网和高程网平差程序,利用GUI对程序进行整合,形成一个测量平差软件,并以实例进行验证分析。通过实例验证,得出如下结论:借助Matlab矩阵计算的强大功能,可方便快捷地实现控制测量的平差计算。Matlab具有数据可视化功能,利用强大的绘图工具及绘图函数,可计算和绘制复杂的曲线,有利于精度分析,具有较强的适用性。

