海-气界面气体交换速率与二氧化碳气体通量的估算
陈元瑞,赵栋梁*,林子宽
( 1.中国海洋大学 海洋与大气学院,山东 青岛 266100)
1 引言
全球碳循环是影响地球气候系统的重要过程,而海-气CO2通量是其中十分关键的一个部分,对于模拟和理解海洋-大气系统的耦合与变化十分重要[1]。目前海-气界面CO2通量的估算大多基于下述块体公式:
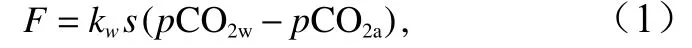
式中,F为CO2气体通量;kw为气体交换速率;s为溶解度(是温度和盐度的函数);pCO2w和pCO2a分别表示海水和大气的CO2分压。
在块体公式的使用过程中,最为关键的就是气体交换速率kw的估计。对于溶解性比较弱的气体,如CO2,海-气界面的气体交换过程主要取决于海-气边界层海水侧的黏性次层和湍流边界层,且与海水侧的湍流强度密切相关,而湍流强度与海上风速、波浪状况和大气稳定度等有关。人们通常将气体交换速率与海上风速和波浪状态相联系,为了便于应用,更多的研究者将气体交换速率参数转化为风速的函数。Boutin等[2]对比了几种较为主流的kw的参数化方法,得到的结果相差达到两倍以上。Takahashi等[3]也指出,目前有关全球生物地球化学碳循环模型误差的主要来源之一就是气体交换速率的不确定性。所以,对气体交换速率kw的深入研究,有利于促进我们对于全球碳循环的认识。
有关kw的估计,基于观测数据,通常经验性地利用风速多项式进行参数化,公式为
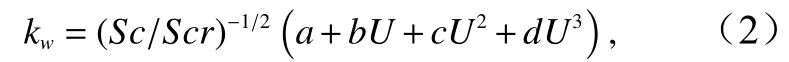
式中,Sc为施密特数,定义为海水运动黏性系数与所测气体的分子扩散系数之比,与海水温度有关;Scr为水温为20°C时对应的施密特数,对于淡水(实验室和湖泊)和海水,Scr分别为600和660;U表示海上风速,一般选用海面上方 10 m 处风速U10;a,b,c,d为待定系数,由观测数据来确定。在早期的研究中,认为气体交换速率为风速的线性函数,近年来,更多研究认为,气体交换速率应该为风速的二次或三次函数,在这方面还存在很多的争议。
本文对于如公式(2),基于实测数据并且争议较小的参数化结果进行了整理,同时在一定的风速区间内,对不同的参数化结果进行比较。利用最新的CO2分压差数据和不同的参数化公式,本文对1982-2018年这37 a全球的海-气界面CO2净通量的变化进行了估算,并对季节变化以及年际变化进行了分析。最后,对气体交换速率参数化未来的发展方向进行了讨论。
2 气体交换速率的观测估算
气体交换速率的观测,主要通过观测风速、CO2分压以及海表面CO2通量,并运用公式(1)计算得到对应的气体交换速率。当下气体交换速率的观测主要有示踪物法和微气象法两类。
示踪物法主要基于物质平衡理论,通过观察海洋以及大气中的目标示踪物(例如222Rn、14C)浓度变化,来对气体交换速率进行计算。这种方法的时间频率及时效性较低,对于建立较为精确的参数化关系有着较大的阻碍。
示踪物法主要分为双示踪法以及热红外法两种。
双示踪法(Dual Tracer, DT)假设不同的气体对于风速有着相同的依赖关系,并在此基础之上通过观察两种示踪气体(3He和 SF6)在一段时间变化的比值,进而对于气体交换速率进行确定。这种方法首先由Watson等[4]提出,Wanninkhof等[5]根据该方法得到的测量数据提出了具体的参数化公式。
热红外法基于表面更新理论,由Jähne等[6]首次提出,并在外海以及实验室进行了诸多实践[7]。其假定热量与气体的海-气交换特征相似,通过计算热量的交换来近似地推测气体交换。该方法可以在分钟尺度上进行观测,同时可以同步对微波破碎以及湍流特征进行测量[8];但是,由于条件限制,无法考虑到气泡这一物理过程对于气体交换的影响[9]。
随着观测技术的不断提高,近年来,微气象法在测量海-气界面气体通量方面得到越来越多的应用,其中,最具代表性的就是涡相关法(Eddy Covariance,EC)。该方法不仅可以在不借助任何经验公式的情况下直接测量气体的通量,而且可以在小时尺度进行持续的测量。Jones和Smith[10]首先将其投入实际运用并测量了海区的通量。但是Broecker等[11]指出,其在海上的观测结果往往信噪比较低,可信程度有待考量。同时,涡相关法在船载和浮标上的测量结果存在显著的差异[12-13],这些差异被归咎于平台本身的运动和风矢量的旋转[14]。Landwehr等[15]指出,对于船载涡相关测量,船只运动带来的风速测量偏差以及船只本身对于风场的扰动这两个因素影响着测量结果的准确性。此外,研究表明,大多数涡相关研究中使用的非色散红外CO2分析仪对水蒸汽具有交叉灵敏度,这导致对气体交换速率的估计中存在很大的不确定性[16]。同时,CO2分析仪具有一定的运动敏感性,可能导致测量的结果产生偏差[17]。
3 气体交换速率的参数化
3.1 风速二次方依赖关系参数化结果
气体交换速率对风速二次方依赖关系的参数化结果分别基于主动物质平衡法、被动物质平衡法(全球14C平衡)和涡动相关法获得的数据。其中,基于同属物质平衡法的前两者得到的参数化结果较为相似,而涡相关法的结果与其他两种方法的结果差异较大。
Liss和Merlival[18]、Nightingale等[19]以及Ho 等[20]运用物质平衡获得了气体交换速率的结果。Liss和Merlival[18]根据风-浪槽实验数据以及湖泊的观测结果,给出了一种三段式的参数化方案(公式(3)),3种情况分别对应着不同风速下的海表面过程。虽然二次关系只出现在低风速阶段,但是该结果可以运用二次关系在0~15 m/s的风速区间较好地近似[21]。通过在外海运用双示踪法测量得到的数据,Nightingale等[19]拟合得到了气体交换速率公式(公式(4)),其是关于风速的二次多项式,作者认为,该方案可以解释数据中总方差的82%[22]。Ho等[20]运用SAGE (SOLAS Air-Sea Gas Exchange)在南大洋通过双示踪测得的数据,在0.6~23.5 m/s的数据区间中,得出了为风速二次方的气体交换速率公式 (公式(5))。与公式(3)以及公式(4)不同的是,这次的测量是在大洋中进行,且包含了高风速(大于16 m/s)的数据。
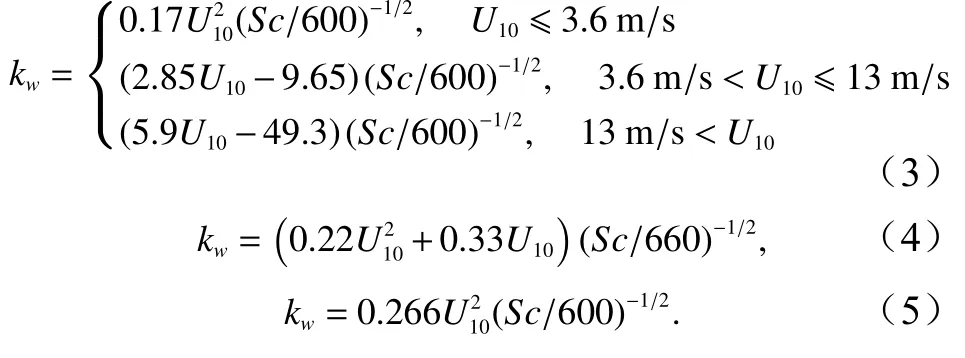
运用全球14C平衡进行估计的主要有3项成果。1992年,Wanninkhof[21]基于全球14C资料拟合得到了气体交换速率与风速的关系,并分别给出了长期气候态平均风速和短期平均风速与气体交换速率之间的关系(公式(6))。但是,其所运用的全球14C的数据可能高于其实际水平[20]。Sweeny等[23]基于新的全球14C数据给出的结果(公式(7))弥合了基于小尺度数据(例如主动双示踪平衡法)与基于被动示踪平衡法的全球大尺度数据(例如14C)得到的参数化结果之间的差距,该方案相比之前基于同类型数据的参数化结果(公式(6))较小。2014 年,Wanninkhof[24]对自身的成果进行了更新,运用最新的14C结果给出了气体交换速率公式(公式(8)),公式(8)与 Sweeny 等[23]的结果十分接近。

Jacobs等[25]于1999年在距离荷兰海岸9 km的海域获得了CO2通量数据,并得到了风速二次方关系的参数化公式(公式(9))。其中,数据所处的风速区间为3.5~15 m/s,系数95% 的置信区间为[0.46,0.63][25]。
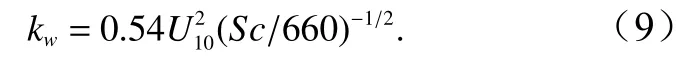
图1a展现的是上述风速二次方关系的参数化结果。值得一提的是,图中所有的气体交换速率均标准化到了Sc=660的k660。可以看到,各种参数化方法在高风速区间存在明显差异。14C和示踪物法得到的参数化结果在图1所示的风速区间内都较为接近,但是涡相关法得到的参数化结果较大,在高风速明显大于其他方法,当风速大于20 m/s时,涡相关法得到的参数化结果甚至可以达到部分其他结果的3倍以上。
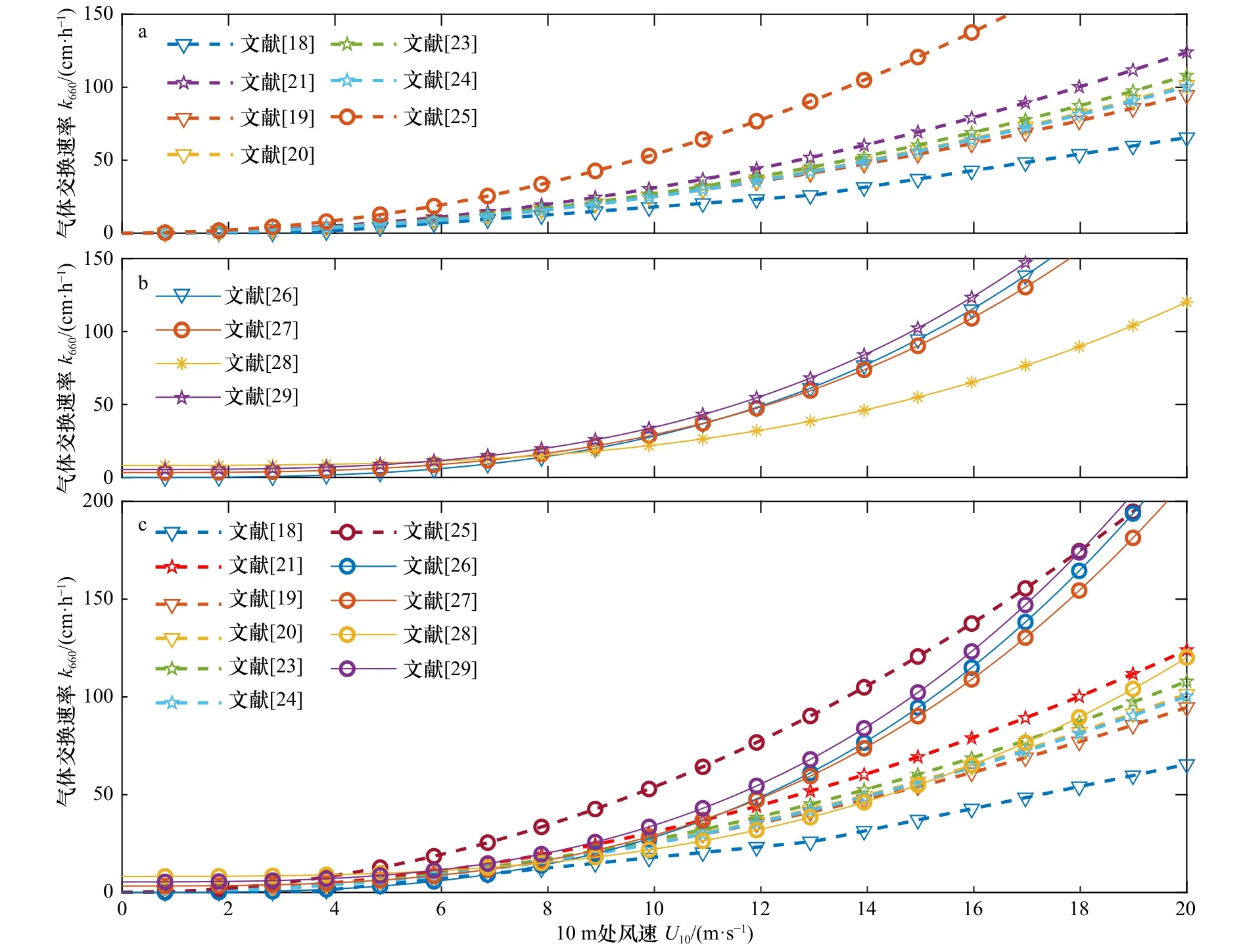
图1 气体交换速率与风速二次方(a)、三次方(b)以及两种依赖关系(c)的参数化结果Fig.1 Parameterization results for quadratic (a) , cubic dependence (b) and both of them (c) between gas transfer velocity and wind speed
3.2 风速三次方依赖关系参数化结果
气体交换速率为风速三次方依赖关系的参数化结果大多是基于涡相关法,观测海区覆盖了较为广阔的海区。其结果在低风速阶段(小于12 m/s)较为接近,由于参数化风速区间不同等原因,在高风速阶段的结果差异较大。
Wanninkhof和McGillis[26]通过分析在北大西洋进行的涡相关研究(Gas EX-98)得到的CO2通量数据以及实验室的结果,发现风速与气体交换速率可以运用风速三次方关系进行描述,并首次提出风速三次方关系的参数化公式(公式(10)),对应风速区间为 0~15 m/s。同样在北大西洋,McGills等[27]运用涡相关数据,得到了包含常数项的风速三次方参数化公式(公式(11))。
McGillis等[28]于2004年,通过分析在赤道太平洋进行的GasEX-2001计划运用涡相关法得到的CO2通量数据,在2~12 m/s的风速区间内,得到了新的风速三次方参数化公式(公式(12)),Edson 等[29]利用在南大洋进行的SO GasEx计划中,通过涡相关法得到的观测数据,同样给出了气体交换速率为风速三次方依赖关系的参数化公式(公式(13)),该公式在0~18 m/s风速范围内与观测数据符合得非常好。
图1b展示了气体交换速率为风速三次方依赖关系的参数化公式随风速的变化,可以看到,与其他的参数化公式相比,McGillis等[28]于2004年得到的公式(12)在风速大于12 m/s时明显偏小,这或许与其所基于的数据风速区间为0~12 m/s有关。
3.3 两种依赖关系的对比
气体交换速率拟合为风速二次方与三次方依赖关系的区别主要体现在低风速与高风速阶段。相比二次方关系,三次方关系在低风速数值较低,而在高风速数值较高。对于高风速情况,波浪破碎以及高风速下气泡对交换过程的强化被认为是可能的原因;对于低风速阶段,即使风速为0时,气体交换速率并不为0,因此有些参数化公式给出了非0截距,试图解决低风速下结果偏低的问题[25-26]。对此,有学者的解释是,海表层附近发生的气体交换过程不能简单地用平均风速表达,从而会出现气体交换速率的非0截距[27]。
图1c展现的是不同作者给出的各种不同气体交换速率参数化结果。可以看到,不同的依赖关系对于参数化结果并不存在决定性的影响。但是,当风速大于12 m/s时,基于涡相关数据获得的拟合结果不论是二次方还是三次方依赖关系,都显著大于其他两种数据的拟合结果。显然,与参数化方法相比,基于不同方法得到的观测数据本身对于最终结果的影响更大。
4 不同时空尺度下的全球CO2通量
4.1 长期平均结果
最近,Bakker等[30]从3 646个数据集中整理了1957-2014年约14 700 000个观测数据,给出了第3代的世界海表CO2分压差数据集(Surface Ocean CO2Atlas version 3, SOCATv3)。Landschützer等[31]通过神经网格插值对SOCATv3数据进行处理,给出了分辨率为1°×1°的月度数据集,该数据集包含了海表CO2分压差ΔpCO2、溶解度s等数据,时间长度为38 a(1982-2019年)。风场数据选用的是欧洲中尺度天气预报中心(European Centre for Medium-Range Weather Forecasts, ECMWF)提供的 1982-2019 年的分辨率为 1°×1°的月度数据集。图2是根据Landschützer等[31]提供的海表CO2分压差绘制的全球ΔpCO2标准气候平均值分布。
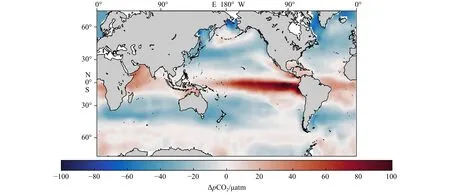
图2 全球ΔpCO2标准气候平均值(1 atm=101 325 Pa)Fig.2 Global ΔpCO2 standard climatological normals (1 atm=101 325 Pa)
图3展示了基于公式(3)至公式(13)共11种气体交换速率公式计算得到的1982-2018年气候态平均的CO2通量37 a均值的全球分布。
图4展示了CO2通量以1°为间隔在不同大洋以及全球大洋沿纬向积分的结果。表1给出了4个大洋在不同纬度年平均的CO2通量。综合图3、图4以及表1 可以看到:赤道太平洋(14°N~14°S)是大气 CO2最主要的源,其气候态平均值(以碳计,下同)为0.38 Pg/a,一个明显的源区是在赤道东太平洋发生厄尔尼诺现象的海域,该区域海水CO2分压明显大于大气的,这可能与该处存在的上升流有关。而大气CO2的汇则主要分布在纬度大于15°的南北半球高纬度海区,其中在南半球40°S附近海域,跨越印度洋、太平洋和大西洋,构成一个几乎连续的强吸收带。在40°N附近海域,也同样在大西洋和太平洋有一个沿纬向分布的强吸收带。南、北半球纬向吸收带的存在应该与西风带有关。同时可以看到,整个北大西洋是大气CO2的强吸收区域(-0.38 Pg/a)这或许与北大西洋海水下沉有关。总体上,南半球和北半球中高纬海区(14°~50°)构成了CO2最为主要的两个汇,其年平均CO2通量分别为-1.144 Pg/a和-0.517 Pg/a。
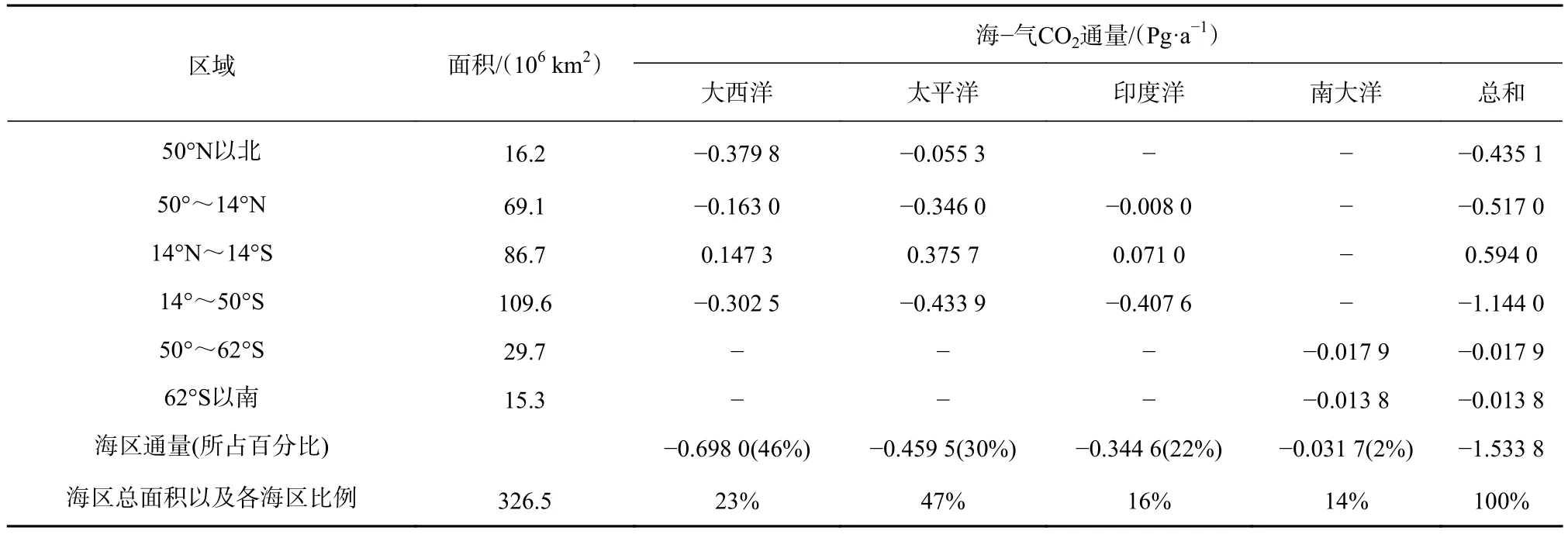
表1 不同参数化结果估计的CO2通量的在不同海区的平均分布Table 1 Mean distribution of CO2 fluxes estimated by different parameterization results in different areas
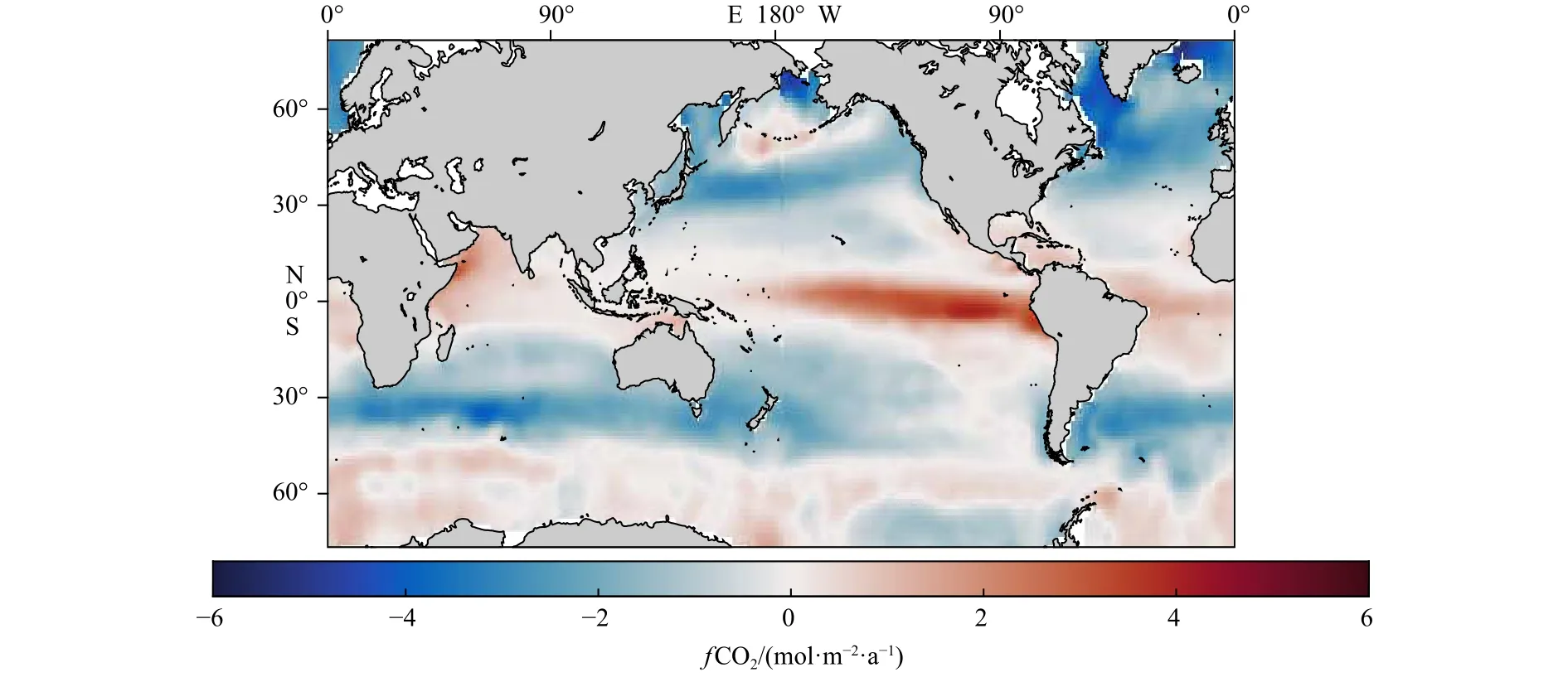
图3 利用不同气体交换速率得到的1982-2018年海-气界面CO2通量平均值分布Fig.3 The average of the results of the air-sea CO2 flux from 1982 to 2018 based on various gas transfer velocities
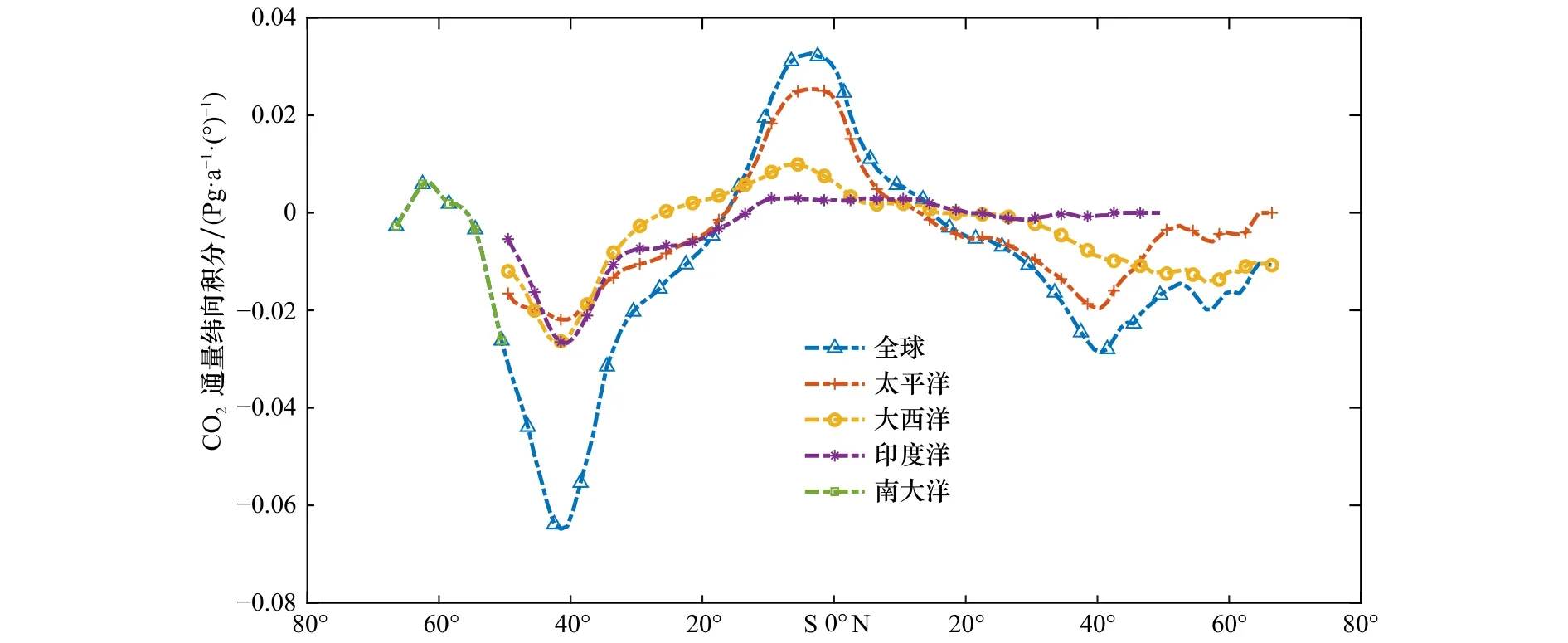
图4 CO2净通量的纬向分布Fig.4 The net CO2 flux obtained by zonal integration
从全球尺度来看,在1982-2018年这37 a平均的全球 CO2通量为(-1.53±0.15)Pg/a。这一结果与 Takahashi等[32]根据最新数据集计算的结果-1.42 Pg/a十分相近,但与最近Iida等[33]的估算结果相比偏小。他们给出的年平均值为(-2.0±0.5)Pg/a,造成这种差异的主要原因是CO2分压数据不同。Iida等[33]运用的CO2分压数据中,海侧的CO2分压是用回归方法由全球海洋总碱度和溶解无机碳计算得到的。
表1同时比较了几大洋气候态年平均的CO2通量。面积最大的太平洋每年吸收的CO2为全球总吸收量的30%,而仅占世界大洋面积23%的大西洋却贡献了世界大洋年平均吸收量的46%。这样的差异产生的一个重要原因是赤道太平洋东岸著名上升流区对CO2的释放(+0.38 Pg/a)。当厄尔尼诺发生的时候,这一地区CO2的释放会显著下降,使得太平洋整体上吸收的CO2增加,与大西洋之间的差异显著减小[34]。
图5展现了根据不同的气体交换速率参数化公式对1982-2018年的全球CO2净通量进行估计的结果。从时间变化的角度来说,不同方法算得的全球CO2通量随时间变化的趋势是一致的,因为该趋势主要取决于CO2分压差数据。从图5可以看到,海洋一直是CO2的汇,我们得到CO2通量的年均值为-2.88~-1.06 Pg/a,相差1.82 Pg/a,其中最大和最小吸收值分别由参数化公式(3)和公式(9)计算得到。
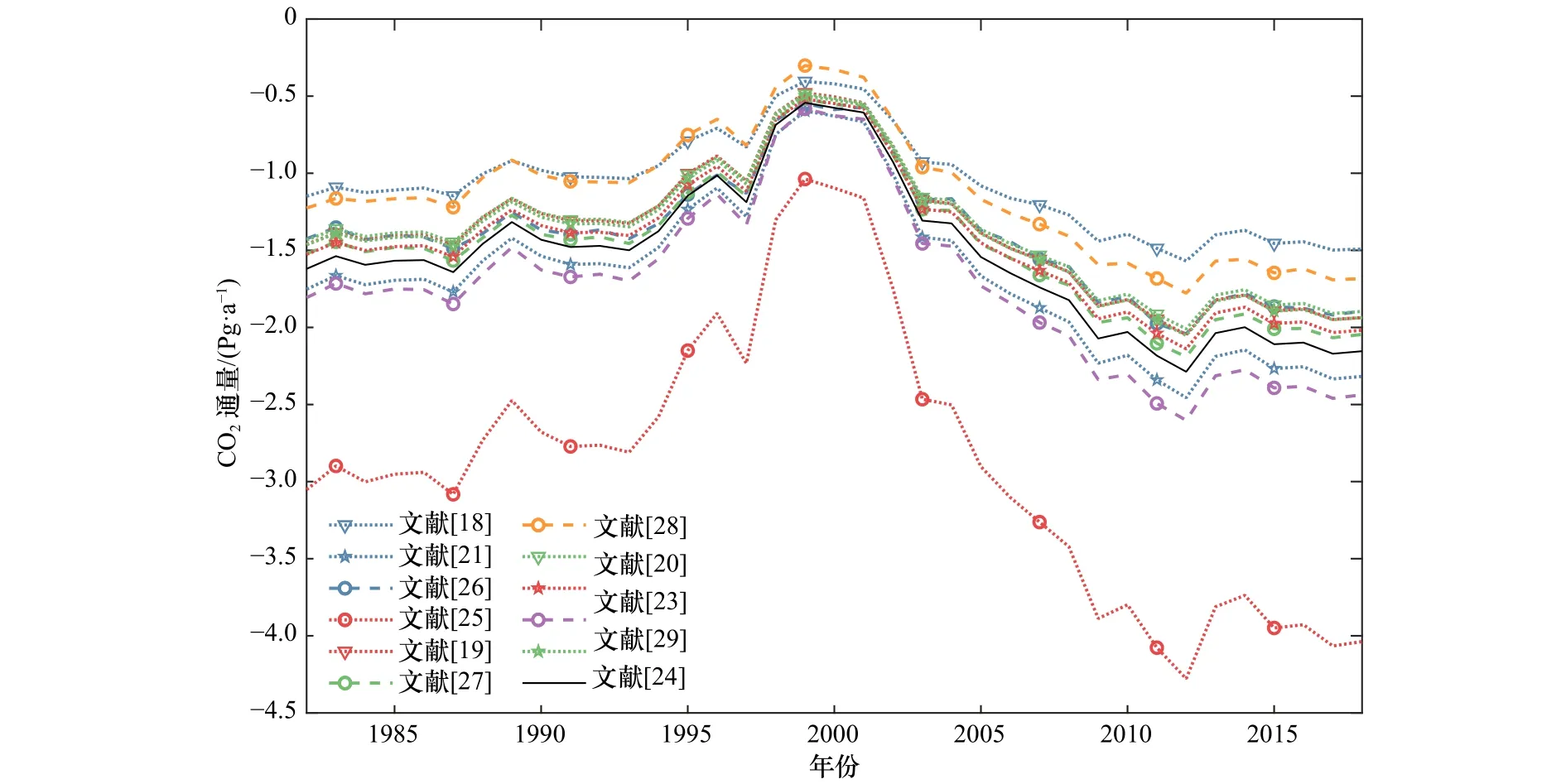
图5 不同参数化方案算得的CO2通量随着时间的变化Fig.5 Variation of CO2 fluxes calculated by different parameterization schemes with time
从时间上来看,海洋的CO2吸收值的最大值在2012年,为3.09 Pg/a,吸收最小值在1999年,为0.75 Pg/a。从长期趋势而言,1999年前,海洋对大气CO2的吸收量逐年减少,而在1999年之后,海洋吸收量开始增大,即1999年是海洋吸收CO2的一个转折年,这一结果与Iida等[33]研究一致,造成这种现象的原因尚不清楚,显然应该与全球变化有关。
为了比较海洋年吸收量最大值和最小值之间的差异,图6给出了用2012年的CO2通量减去1999年的CO2通量的结果。可以看到,2012年南大洋和大西洋北部区域对CO2吸收加强,两者相比,南大洋对二氧化碳的吸收明显增强,起着更为重要的作用。对于赤道地区,2012年释放CO2增多,但幅度不大。
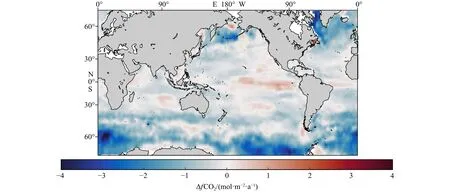
图6 2012年的CO2通量与1999年的CO2通量的差值Fig.6 Subtract the CO2 flux in 1999 from the CO2 flux in 2012
图7展示了基于不同测量方法得到的气体交换速率给出的CO2净通量。从图7可以看到,基于涡相关数据的参数化结果在计算总CO2通量的时候比其他方法大20%左右。由此可见,数据的获取方式对气体交换速率参数化的结果起着主导作用。与Takahashi等[3]的观点不同,对于CO2通量的估算大小,更多取决于参数化方案的数据观测方式,而不是气体交换速率与风速的幂次关系。
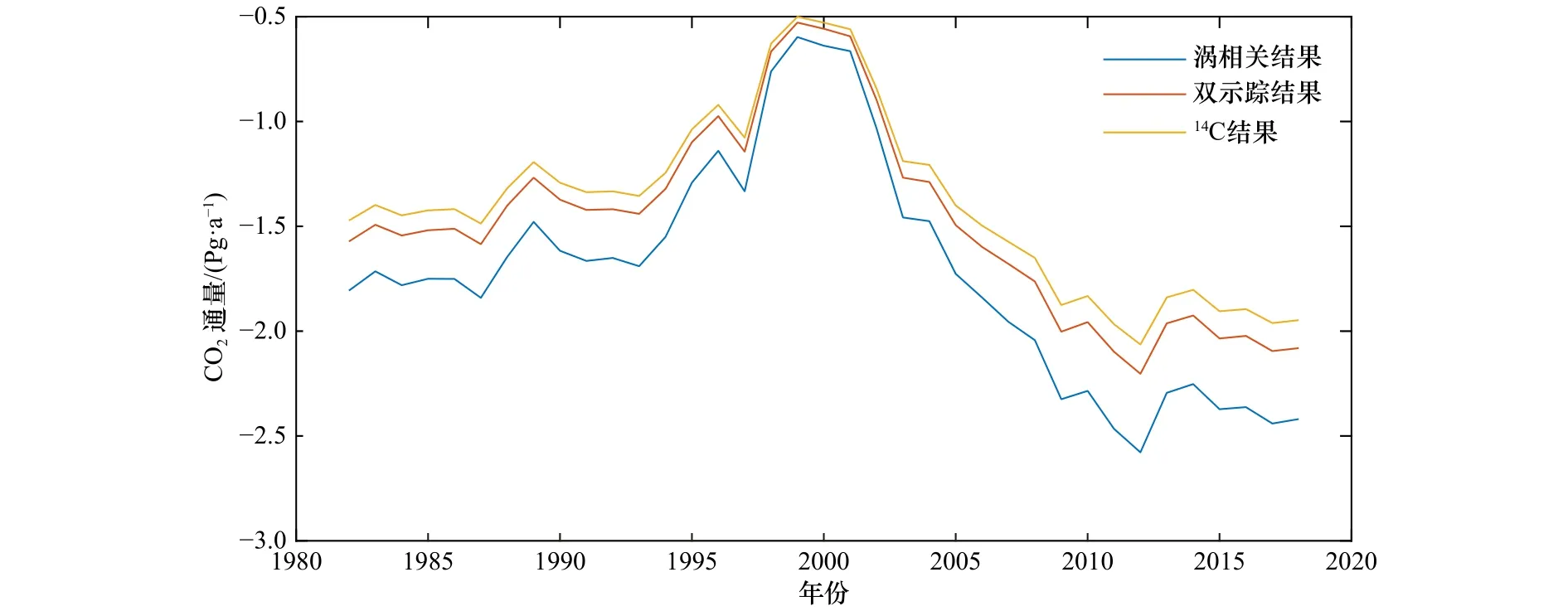
图7 基于不同观测数据得到的CO2通量随着时间的变化Fig.7 Variation of the CO2 fluxes with time for different measurement schemes
4.2 季节变化
全球大洋CO2通量的气候态平均结果随月份的变化如图8所示。值得一提的是,这并非某一个参数化方案计算的结果,而是所有参数化方案的平均。可以看到,热带东太平洋地区一直是CO2的源;而高纬度海区则一直处于吸收状态。季节性变化最为明显的是西北印度洋。由6-8月强烈的季风带来了较高的气体交换速率,使得该地区在这些月份成为了CO2的源。
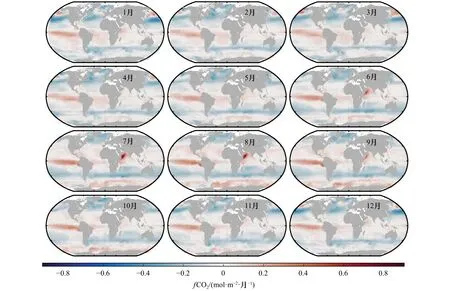
图8 全球大洋CO2通量的气候态平均结果随月份的变化Fig.8 The monthly climatological average CO2 flux in global ocean
图9展示了CO2通量以1°为间隔在不同大洋以及不同的气候带沿纬向积分的结果。整体上,热带大洋一直在释放CO2且季节变化较小,其中,太平洋的CO2通量最大,月平均释放量达到了1 g/m2。大西洋、太平洋和印度洋北半球的温带区域CO2通量(图9a至图9c红线)呈现明显季节变化,冬季吸收强烈夏季减缓,在7-9月3个大洋通量均为正,向外释放CO2。这是随季节变化的海表面温度对于CO2分压的作用结果。值得一提的是,由于印度洋特殊的海陆结构形成的季风使得印度洋的北半球温带的曲线(图9c红线)整体高于大西洋与太平洋。
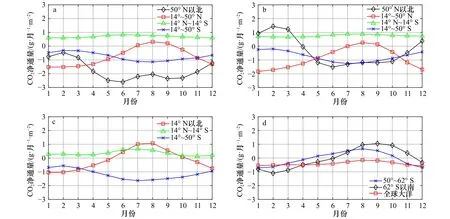
图9 大西洋(a)、太平洋(b)、印度洋(c)和南大洋(d) CO2净通量分布Fig.9 The net CO2 flux of Atlantic Ocean (a), Pacific Ocean (b), Indian Ocean (c), and Southern Ocean (d)
图10展示的是所有参数化方法平均得到的气体交换系数(气体交换速率与溶解度的乘积)在不同大洋的分布。对于每个洋区进行独立的观察发现,气体交换系数随着纬度增大而不断增大,同时季节性变化不断增强。其中,南大洋的极圈内较为特殊(图10d中黑线),该处纬度较高但是风速相对较低,故气体交换系数整体较低。从全球大洋角度观察,由于受季节变化影响较小且风速相对较低,热带大洋的气体交换系数(图10中绿线)随月份的变化较小并稳定在相对较低的范围。与之相反的是北大西洋的极地地区(图10a中黑线)和南大洋(图10d中蓝线)。这两个地区在各自冬季对应的月份风速较高,气体交换系数均达到了 0.12 (g·m-2)/(mol·μatm)(1 atm=101 325 Pa)。但是在夏季,这两个的地区的气体交换系数下降到了 0.05(g·m-2)/(mol·μatm)和 0.08(g·m-2)/(mol·μatm),季节变化十分明显,这一定程度上和溶解度随温度的变化有关。对于大西洋、太平洋和印度洋北半球温带区域的气体交换系数(图10a至图10c中红线)进行观察可以发现,印度洋的气体交换系数的变化与其他两个大洋的变化方式相反,这是由于印度洋独特的季风气候,使得印度洋的夏季拥有比冬季更高的风速。
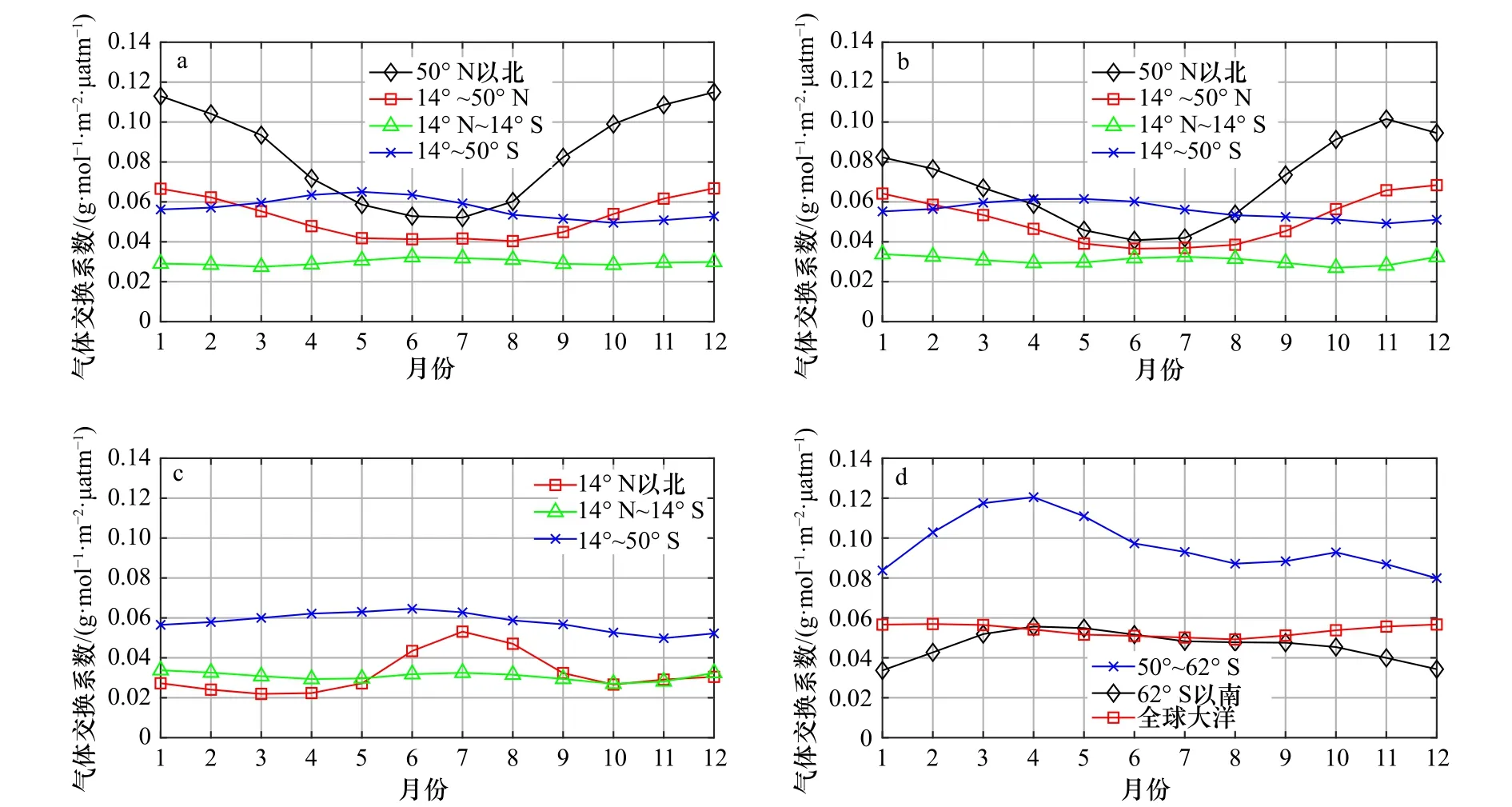
图10 大西洋(a)、太平洋(b)、印度洋(c)和南大洋(d)的气体交换系数(1 atm=101 325 Pa)Fig.10 The gas transfer coefficient of Atlantic Ocean (a), Pacific Ocean (b), Indian Ocean (c), and Southern Ocean (d) (1 atm=101 325 Pa)
图11从上到下依次展现的是1983-2018年在赤道上135°E~105°W区域的海温变化、pCO2变化以及此期间对应的Niño3.4指数。ENSO事件处于暖位相时,赤道东风整体减弱,东岸增暖[35-36]。在图11中可以更清楚地看到,当Niño3.4指数为正的时候,赤道太平洋整体偏暖,同时伴随着CO2通量减小。这与历史上几次厄尔尼诺事件(1982-1983年、1986-1987年、1991-1994年、1997-1998年、2002-2005年、2006-2007年、2009-2010年和2015-2016年)是一致的。
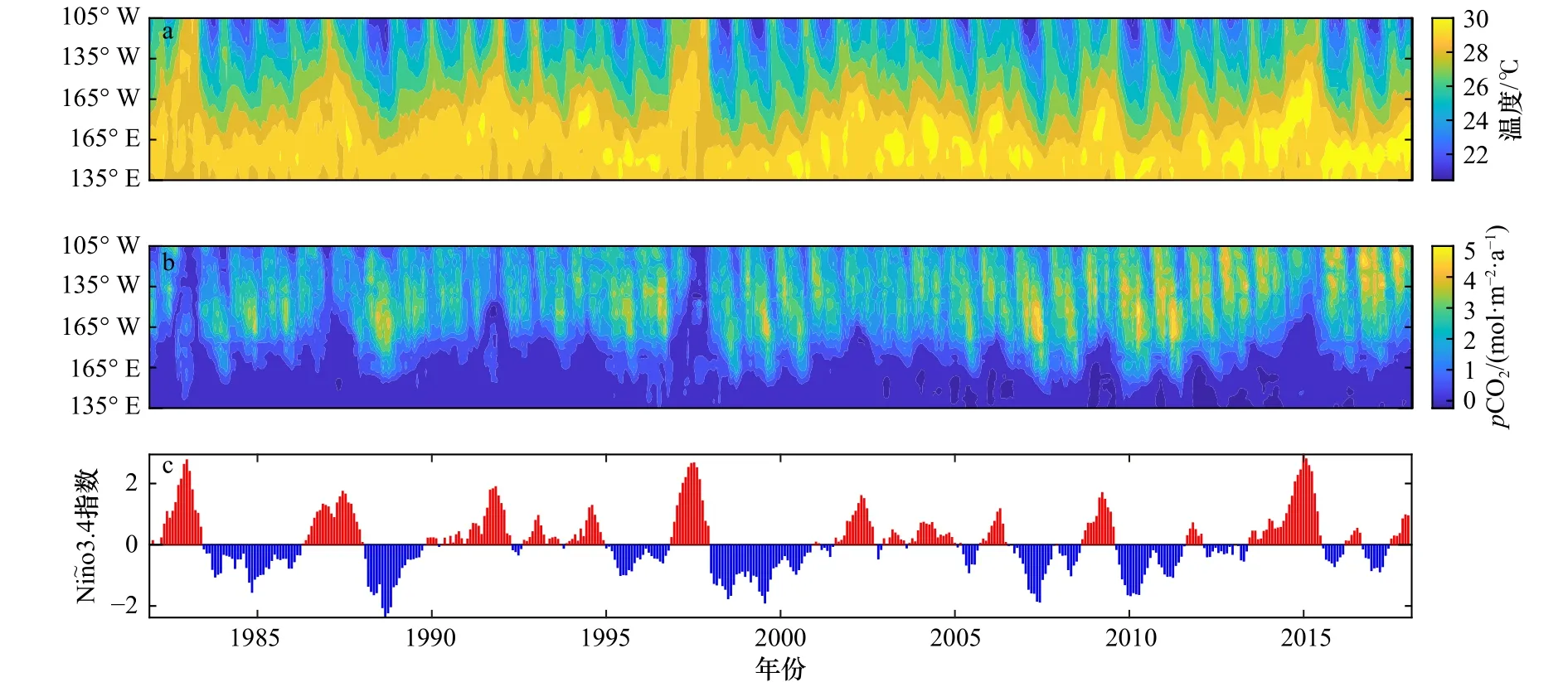
图11 1983-2018年赤道上135°E~105°W的海温变化(a)、pCO2变化(b)以及此期间对应的Niño3.4指数(c)Fig.11 SST variation (a), pCO2 variation (b) and the corresponding Niño3.4 index (c) over the equator from 135°E to 105°W from 1983 to 2018
4.3 年际变化
图12展现的是1983-2018年的Niño3.4区域的年平均 CO2释放量(蓝线)与 Niño3.4 指数(红线)。图中ENSO事件对应的时间内,Niño3.4区域内的CO2通量出现了明显的变化。这说明赤道太平洋上的海温异常与该区域的年平均CO2通量存在明显的相互影响。
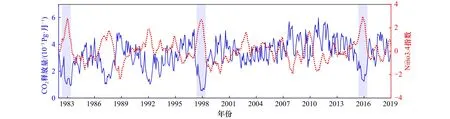
图12 1983-2018年的Niño3.4区域的月平均CO2释放量(蓝线)与Niño3.4指数(红线)Fig.12 Monthly mean CO2 flux (blue line) and Niño3.4 index (red line) for the Niño3.4 region from 1983 to 2018
5 讨论和结论
目前对于气体交换速率的参数化所存在的问题,学者们主要提出了以下两点:高风速和无风状态下海-气气体交换物理机制尚不清楚、用风速作为单一变量进行参数化标准的局限。
Krall等[37]对高风速下气体交换速率的研究指出,高风速下物理机制需要进一步研究,这涉及到波浪破碎产生的强湍流、大量气泡和海洋飞沫如何影响海-气交换过程。McGillis等[27]指出,在极低的风速条件下,由于海-气界面的通量非常小,CO2通量难以观测,这使得我们对于该状态的气体交换机制知之甚少,此时需要考虑海面附近黏性次层和表面张力对交换过程的影响。因此,需要考虑除了风速之外其他因素对于气体交换速率的影响[28]。事实上,有很多研究者指出,仅采用风速对气体交换速率进行参数化的局限性。
Zhao等[38]考虑波浪状态对气体交换速率的影响,用波浪的谱峰角频率、空气摩擦速度和黏性系数定义了风海雷诺数,以此对气体交换速率进行参数化计算。Zappa等[39]考虑了波浪的微破碎对气体交换速率的影响。Rutgersson等[40]研究了对流混合对于气体交换速率的影响,Salter等[41]通过实验证明了水表面的表面活性物质对于气体交换速率有影响。另一方面,对于高风速下较高的气体交换速率,由三次方依赖关系可知,该过程中气泡对于交换的强化作用是一个重要因素。Gu等[42]指出,高风速时气泡在气体交换速率和海气[42]中发挥着极为重要的作用,在高风速时,气泡介导的气体交换大约贡献了总通量的50%。但是,Krall等[37]在实验室对风速达到85 m/s时气体交换速率的最新研究显示,对于CO2这样的低溶解度气体,气泡对于气体交换速率的贡献十分有限。实验中,当风速达到33 m/s之后,气体交换速率急剧上升。对于这一现象,Krall等[37]认为当前缺乏成熟的理论提供解释。Bell等[43]对二甲基硫和CO2气体传输速度的同时测量显示,在中、高风速下,两种气体(二氧化碳和二甲基硫)之间的气体传输存在显著差异。这些数据表明,波浪破碎后,气泡介导的气体输运对CO2的影响很大。
影响气体交换速率准确参数化的另一个重要原因是观测数据覆盖范围和准确度的限制。对于低风速情形,通量观测的不足,使得参数化方程中的非0截距难以确定。对于高风速情形的观测数据仅有实验室结果,缺少外海观测数据,在观测技术方面存在很大的困难,在如此风高浪大的恶劣环境下,几乎所有的观测仪器都变得不可靠。从观测方法的角度来看,双示踪法需要的观测时间较长,在实际应用中,无法保证在高海况保持长时间的平稳性。对涡相关法,高风速下由于波浪破碎,产生大量的海洋飞沫,在海面上方形成空气和水滴混合的过渡层,此时,海-气界面的确定存在非常大的模糊性,同时,海洋飞沫直接影响测量仪器的数据采集,使得高风速下涡相关法测量海-气界面通量面临巨大挑战。
本文对前人用风速对气体交换速率进行参数化的工作进行了比较分析,发现参数化方案无论采用风速二次方或三次方多项式,在中等风速时的差异并不明显,只有推广到高风速情形,两者差异变大,但造成这种差异最根本的原因在于观测数据获取的方式,基于涡相关法比基于物质平衡法获取数据得到的气体交换速率更大。在此基础上,用多种不同气体交换速率参数化公式对1982-2018年间全球海-气界面CO2通量进行了估算,海洋CO2通量的年平均值为(-1.53±0.15)Pg/a。在南北半球40°附近海域,存在沿纬向的大气CO2吸收带,这与西风带有关,而整个北大西洋是强吸收区,应该与北大西洋海水下沉有关。从时间尺度上来看,1999年之前,全球大洋二氧化碳吸收量逐年减小,1999年达到最小值,之后开始逐渐增大,2012年似乎存在一个小峰值。进一步的分析表明,这种增大主要发生在南大洋海区,其物理机制尚不清楚。

