基于模态分析的水下航行器尾舵结构优化

王志斌，赵 坚，宁 凡，刘 聪，黄凯伦，王志伟，高志鹏，刘祉繁，侯景嵘

（天津城建大学 控制与机械工程学院，天津300384）

水下航行器是海洋中一种用于科学考察、环境监测和资源勘探的重要工具，控制其运行姿态的主要机构有尾舵和螺旋桨联合控制两种，其中尾舵控制具有成本低廉，操作简单且稳定性高等优点，因此多用作水下航行器的姿态控制机构.水下航行器尾舵由于发动机旋转零部件的动不平衡特性以及水下的波浪涌动等，其本身容易产生振动，并直接影响水下航行器的运行姿态.国外学者已经对水下航行器进行了大量的研究分析，Hwang，Arom等学者考虑水下航行器的推进器系统产生的振动会从船尾传递到船首，其所传递的振动会影响水下航行器搭载的声呐系统的性能，因此对某小型水下航行器在空气中的振动特性进行了试验研究，得出了较为准确的试验结果[1]；韩国的Min-Sang Seong等学者利用有限元技术对水下航行器结构进行动力学建模，研究航行器结构的模态特性，将模态分析的数值结果与试验模态结果进行比较，对水下智能航行器结构的振动控制性能进行了评价[2]；目前国内一些高校的学者也已经对水下航行器进行了许多研究，海军工程大学曲铎采用CFD-LES理论、Light hill声学模拟理论和振动声学理论对梯形舵翼在不同舵角下的流场和声场进行了数值模拟并分析了水动力激励下流体噪声的特性[3]；大连理工大学的白瑜光等学者在精确有限元建模的基础上对高超声速飞行器的尾舵进行了模态分析，计算了尾舵结构的弯曲和扭转模态，为验证计算的准确性，进行了地面振动试验[4].国内对于水下航行器尾舵进行的动态研究尚且较少，在水下航行器尾舵的设计生产过程中仅考虑其静态特性，往往忽略了实际工作中尾舵与水下航行器主体结构的振动而导致尾舵的额外损耗甚至产生故障，更严重者会降低水下航行器运行姿态的准确性、稳定性，降低其使用寿命.为保障水下航行器在使用过程中的平稳运行，在水下航行器尾舵设计之初，需对其进行动态特性研究[5].

本文通过有限元分析软件和模态试验测试分别对水下航行器尾舵进行动态特性研究.通过模态分析，获得尾舵的模态参数，分析尾舵的振动变形情况，进而提出两种优化的尾舵结构，并对其进行计算模态分析，得出两种优化尾舵的模态参数，同时与三级海况频率进行对比，确定最合适的尾舵优化结构.

1 原始尾舵模态分析

尾舵作为水下航行器的重要零部件，广泛应用于水下探索领域.尾舵的结构动力特性很大程度上决定了水下航行器的适航性[6].不同的海况会激起不同的振动模态，会导致不同形式、程度的变形，并且会影响尾舵的稳定性，进而影响到水下航行器的运行姿态，因此对尾舵进行模态分析是必不可少的.水下航行器尾舵作为连续体，具有无穷多个自由度[7]，其动力学方程如下

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；x为节点的位移；x˙为节点速度；x¨为节点的加速度；F为外力向量.本文研究的水下航行器尾舵阻尼较小，近乎忽略，模态分析时可视为n自由度无阻尼自由振动，即C=0，F=0，固有频率和振型可转化为求解特征值和特征向量的问题[8]，其自由振动方程可表示为

水下航行器尾舵的自由振动可分解为简谐振动的叠加，因此可假设简谐振动的解为

式中：ω为简谐振动的频率，θ为常数项.将式（3）带入式（2）可得

式中：ω2为特征值，A为特征向量.

式（4）为关于A的n元线性齐次方程组，此方程组拥有非零解的充分必要条件是它的系数行列式为零，即|K-ω2-M|=0.此行列式为系统的频率方程，频率方程的n个根对应系统的n个固有频率ωi（i=1，2，3，…，n）[9]，将得到的ωi（i=1，2，3，…，n）分别带入式（4）中，即可得到相应的系统振型向量Ai（i=1，2，3，…，n）.

本文以某款水下航行器的原始尾舵作为参考，对其进行模态分析.原始尾舵形状尺寸如图1所示.

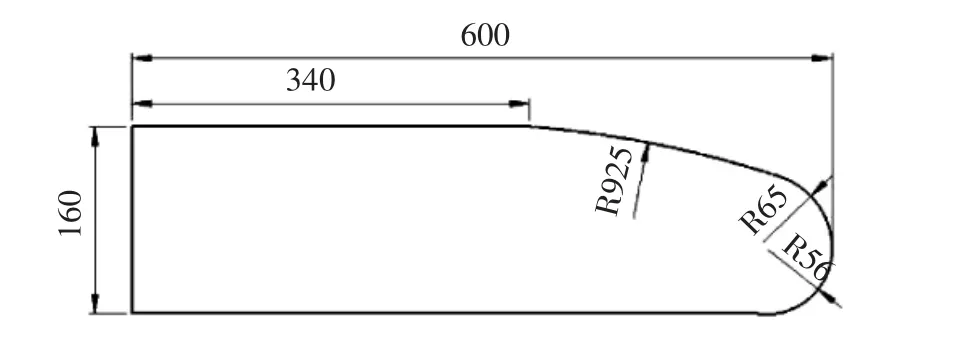
图1 原始尾舵形状尺寸

绘制出原始尾舵的三维实体模型，并保存xt格式，导入至ANSYS Workbench软件中.原始尾舵由6061铝合金材料制成，由此设置其弹性模量为7.1×1010Pa，泊松比为0.33，材料密度为2770 kg/m3.选用四面体和六面体结合的网格类型，网格大小设置为3 mm，得到75124个节点数和10563个单元.原始尾舵网格划分如图2所示.

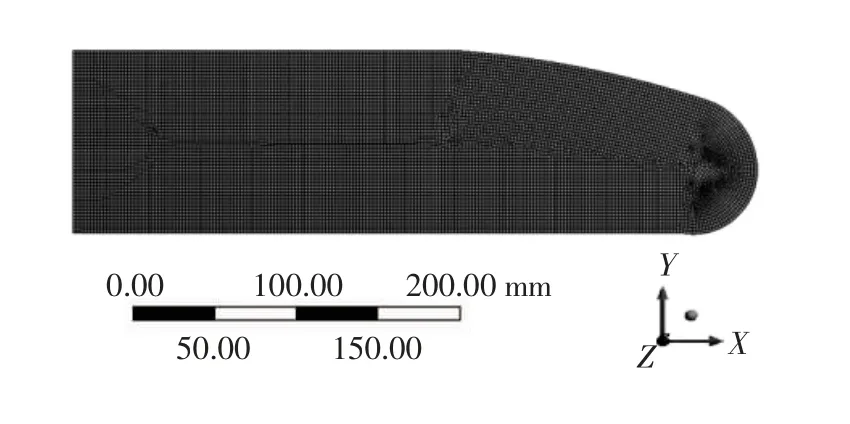
图2 原始尾舵网格划分

同时对原始尾舵进行试验模态分析，搭建试验模态测试系统，使用弹性绳将原始尾舵吊起，采用多点激励多点响应的方法.使用电磁激振器在模态参考点施加激励，激励信号的频率范围为0～1300 Hz；使用加速度传感器拾取响应信号，在原始尾舵上布置35个测点，选择18号测点作为模态参考点，即激励点，测点布置如图3所示.运用特征系统实现算法（ERA）识别原始尾舵的试验模态参数.模态测试系统原理如图4所示，试验系统搭建如图5所示.

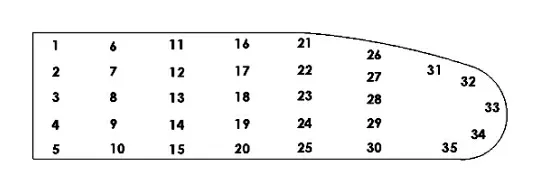
图3 原始尾舵测点布置

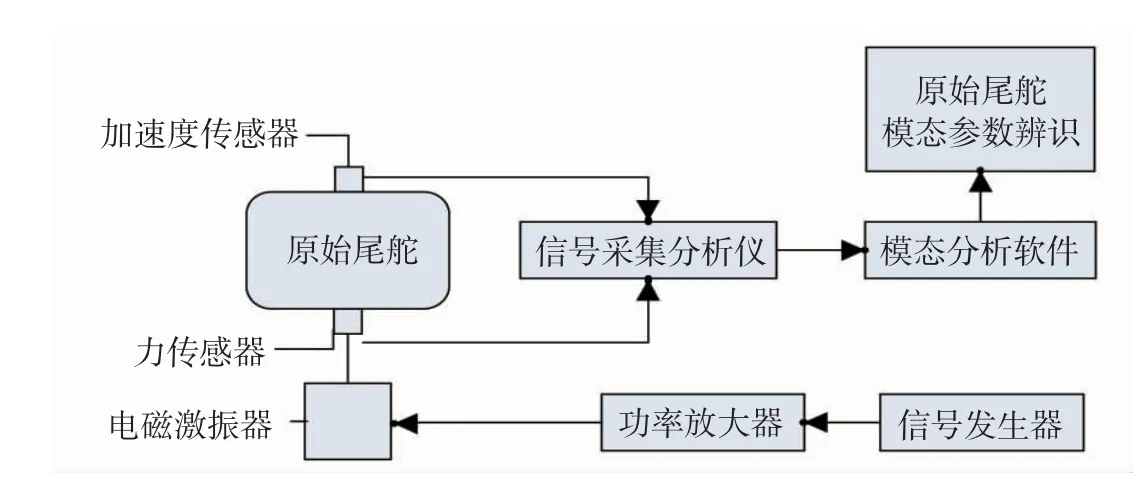
图4 试验测试系统原理

图5 试验系统搭建

本文通过分析软件及模态测试系统分别对原始尾舵进行计算模态分析和试验模态分析，均得到原始尾舵的固有频率及振型.在0～1300 Hz频率范围内，对原始尾舵进行自由模态分析，剔除刚体模态和虚假模态后选取原始尾舵的部分计算模态结果.使用ERA识别原始尾舵的试验模态参数，得到相应的频率及振型结果.尾舵FEA和EMA频率结果对比如表1所示，图6为模态振型对比.

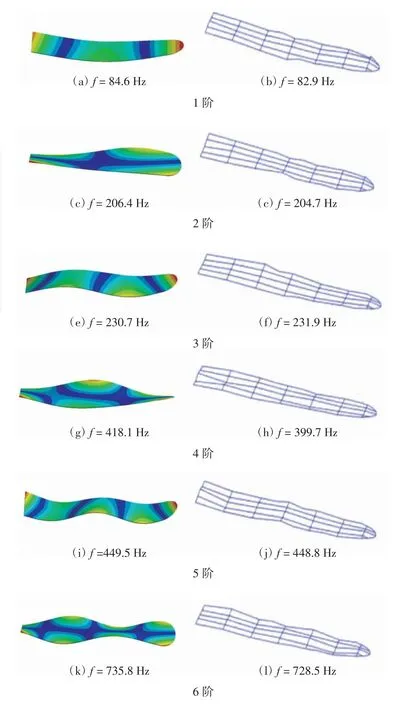
图6 原始尾舵FEA振型与EMA振型对比

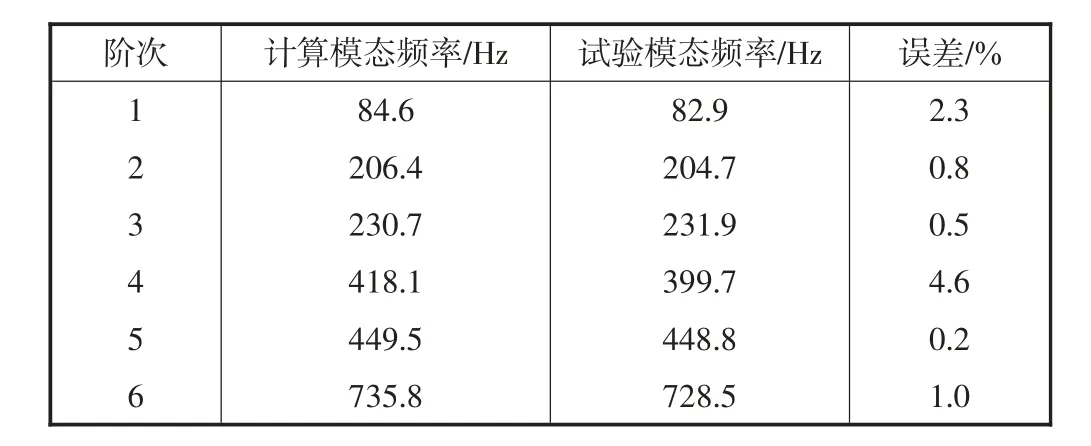
表1 原始尾舵计算模态与试验模态频率对比

通过观察原始尾舵的模态振型图可知，原始尾舵在1阶、3阶和5阶频率处，分别出现1阶弯曲形态、2阶弯曲形态和3阶弯曲形态；在2阶、4阶和6阶模态频率处分别出现1阶扭转形态、2阶扭转形态和3阶扭转形态，且最大变形均发生在原始尾舵的首尾两端.

由原始尾舵FEA和EMA的结果对比可知，频率最大误差发生在4阶模态处为4.6%.同时结合FEA和EMA的振型结果，可以看出两种结果的模态振型具有较高的一致性，由此可以通过原始尾舵试验模态测试验证尾舵有限元模型的准确性和可行性，为尾舵的设计及优化提供了可靠的数据.

2 水下航行器尾舵结构优化

依据原始尾舵的计算模态和试验模态分析结果，可知原始尾舵易产生变形的部位在首尾两端，分析其原因主要是原始尾舵长宽比太大.

本文基于原始尾舵的模态试验结果，分析其易产生变形的原因及变形部位，结合三级海况特征，提出两种水下航行器尾舵的结构优化方案.两种优化方案均缩小尾舵的长宽比，并根据航行器在水下的运行姿态要求，将尾舵主表面修改为倒梯形，即使得梯形的斜边沿水下航行器前进方向；在尾舵上部水平设计一块六边形方板，且使方板锥子头向前，使得尾舵利于破开海水，便于调整水下航行器运行姿态.两种优化的差别在于尾舵主表面的厚度，优化一的主表面平均厚度为15 mm，优化二的主表面平均厚度为25 mm，优化一和优化二的几何模型如图7和图8所示.

图7 优化一尾舵模型

图8 优化二尾舵模型

由上述内容可知，通过试验模态测试已验证尾舵计算模型的准确性，因此只需对优化一尾舵和优化二尾舵进行计算模态分析即可.

将两种尾舵导入至ANSYS Workbench中，对二者设置与原始尾舵相同的材料属性及网格划分，优化一尾舵有66135个节点和38074个单元，优化二尾舵有55036个节点和30957个单元.优化尾舵网格划分如图9所示.

图9 优化尾舵网格划分

计算得出两种优化尾舵的模态频率如表2和表3所示，模态振型分别如图10及图11所示.

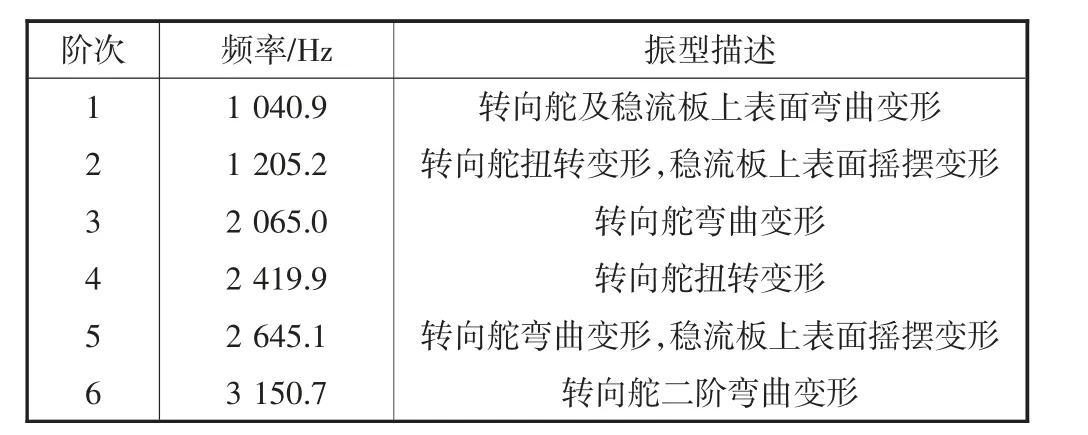
表2 优化一尾舵模态频率

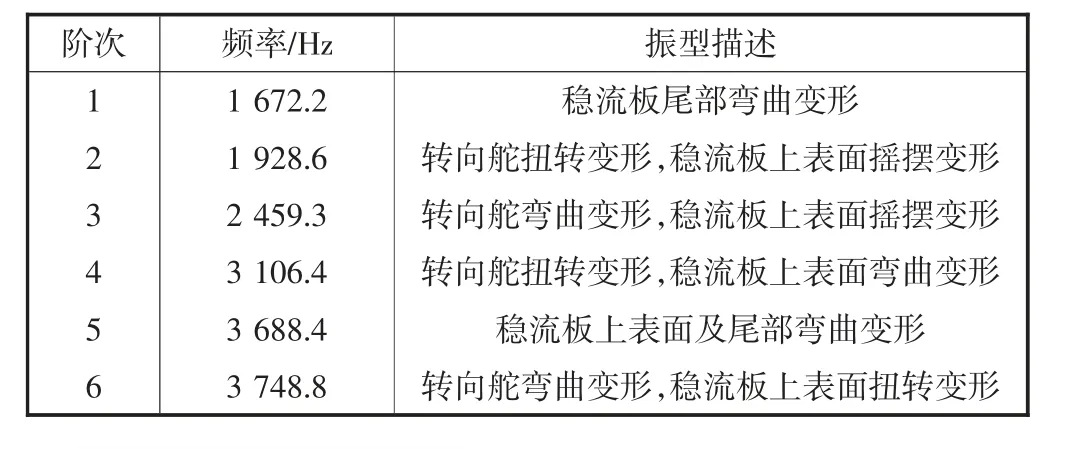
表3 优化二尾舵模态频率

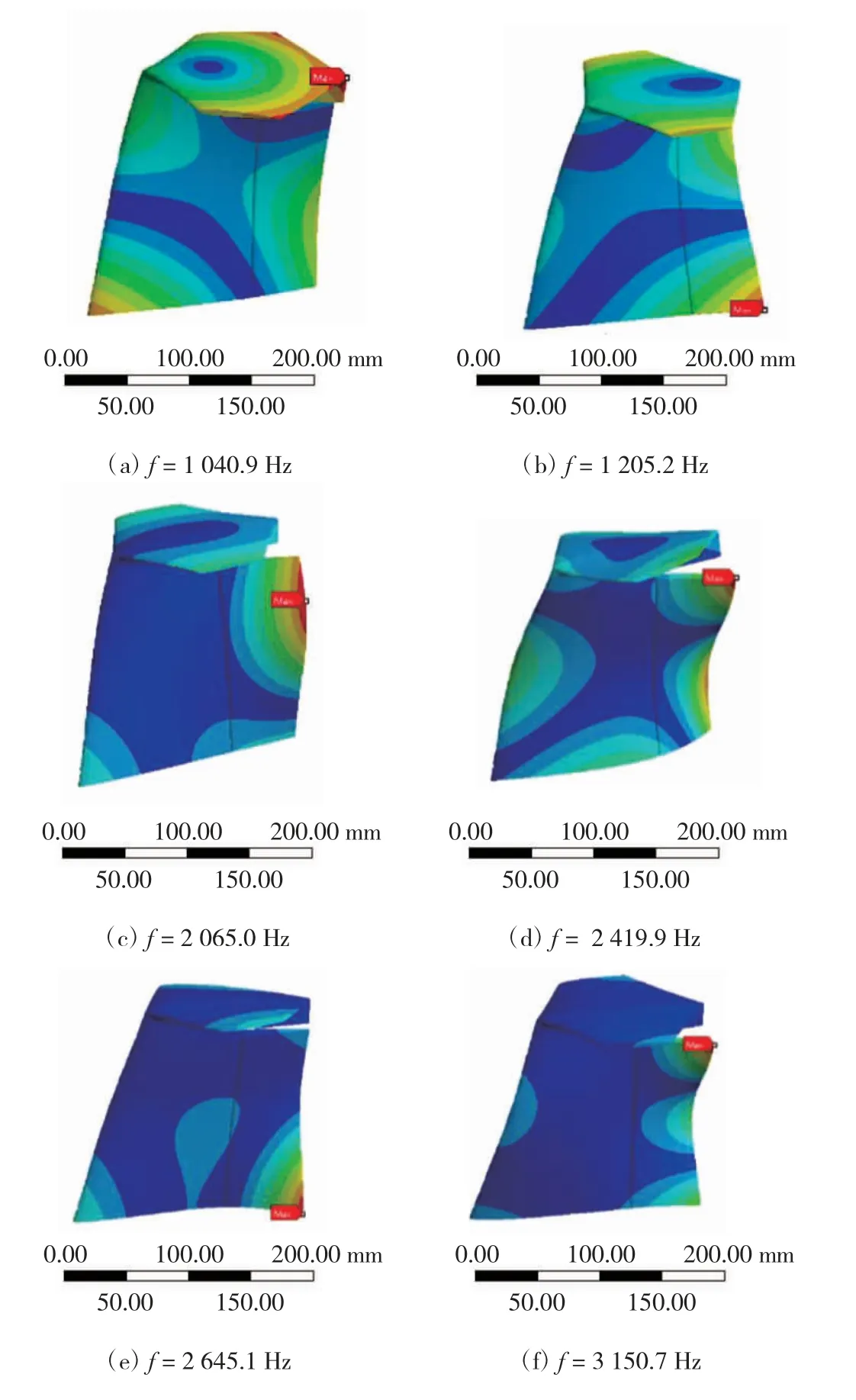
图10 优化一尾舵振型

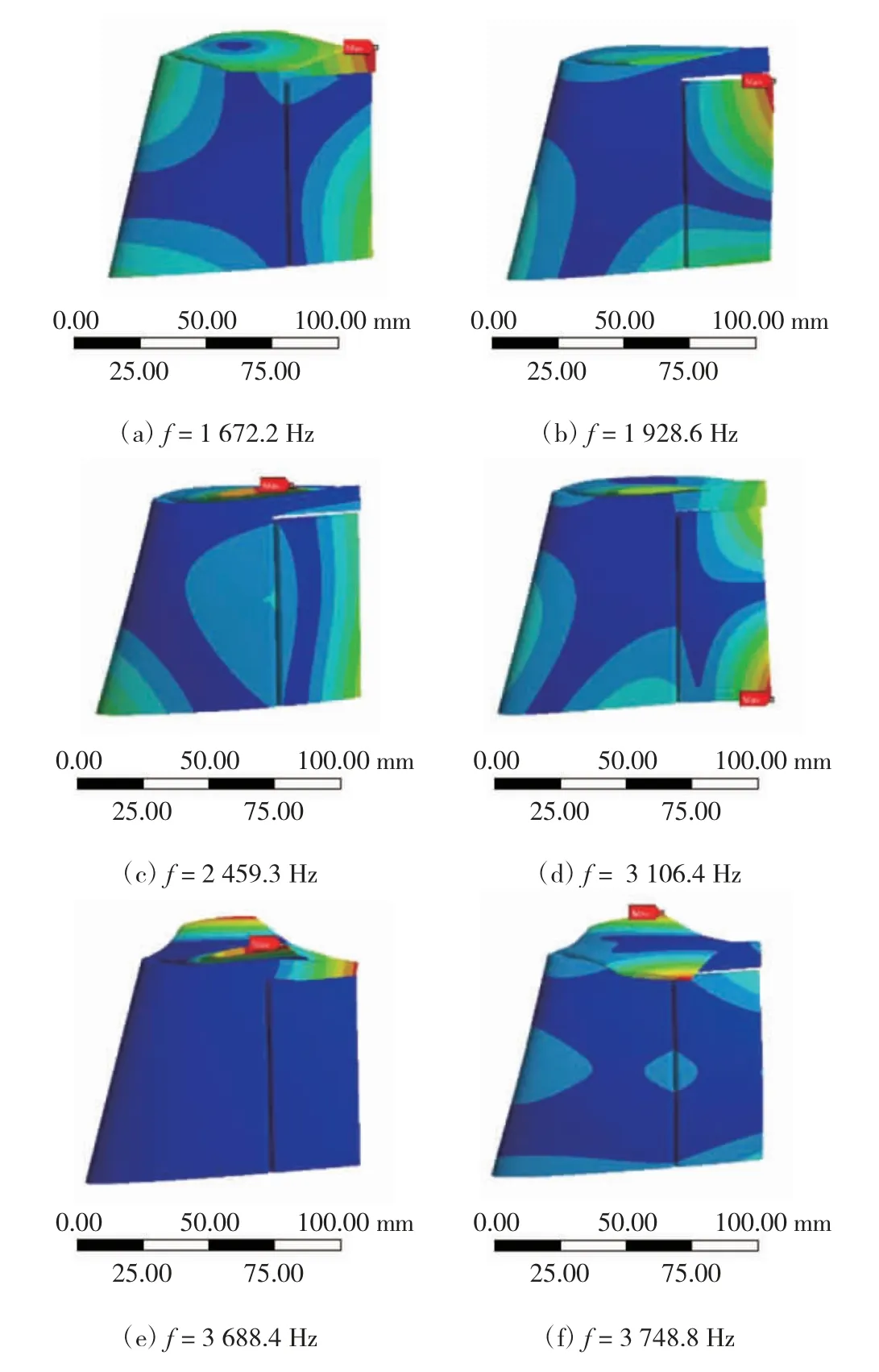
图11 优化二尾舵振型

3 优化尾舵结果分析

结合两种优化尾舵的计算模态分析，可知两种优化尾舵的各阶模态频率均明显大于原始尾舵的模态频率，且优化二尾舵各阶模态频率均大于对应的优化一尾舵各阶模态频率.分析两种优化尾舵的振型云图，可知易产生变形的位置相较于原始尾舵的首尾两端均变为转向舵及稳流板的上表面，由此说明两种优化尾舵的转向舵及稳流板上表面易产生弯曲及扭转变形，是尾舵的薄弱环节.

在真实海洋环境中，三级海况是最常见的一种海况，对应的海面状况是轻浪，其海况特征为浪高约0.5～1.25 m，对应的是海面风速为5.5～7.9 m/s的和风.依据随机海浪理论，海浪周期越长，其频率越低，且传播速度越快，根据深水波公式，海浪频率可表示为其中：C为海面风速，由此可得出三级海况下的频率范围约为0.197～0.284 Hz.由此可知两种优化尾舵各阶模态频率均远大于三级海况的频率，均可避免发生共振现象.

4 结论

（1）通过对原始尾舵进行计算模态分析和试验模态分析，得到6阶固有频率及振型，分析其薄弱环节位于首尾两端，对比计算模态与试验模态结果，频率误差仅在4.6%以内，验证了有限元模型的准确性.

（2）基于原始尾舵的计算模态和试验模态分析结果，以及有限元模型的准确性，提出两种优化尾舵，并进行计算模态分析，分别得到6阶模态频率及振型.

（3）通过随机海浪理论及深水波公式，计算得到海洋中最常见的3级海况的频率范围，并与两种优化尾舵的各阶频率进行对比，可知优化后尾舵低阶频率远大于3级海况的频率范围，并以优化二尾舵更为明显，因此，优化二尾舵更适用于水下航行器.