基于协同组合的新型微混合器的数值模拟
马广志, 沈春银, 董 浩, 戴干策
(华东理工大学国家重点化学工程联合实验室, 上海 200237)
自20世纪80年代微通道技术用于微电子器件的散热研究以来,微通道器件的结构设计优化与性能提升研究日益深入[1]。将微通道作为反应场所,微通道反应器则可以在较小的空间距离及较短的时间内实现扩散混合,因而在样品浓缩、化学合成、化学反应、聚合、提取和纯化、生物学分析和液滴乳化等过程中广为应用[2]。要使微通道器件实现所需功能,关键是结构设计。马欣荣等[3]设计了Y型分叉仿生微通道热沉,优化的分叉角为60°、分叉级数为2级,换热性能的数值模拟研究结果表明,相较于直通道热沉,在相同换热面积与入口速度下改善了温度均匀性并提高散热容量,其压降下降了近40%。姜云峰等[4]基于自相似分形理论设计了一种2级Y型微流控浓度梯度芯片,采用COMSOL Multiphysics软件耦合速度场与浓度场方法,对不同进样和浓度矩阵的微流控芯片进行了数值模拟和实验研究,实现了幂指数形及蝴蝶形浓度梯度分布。陈宏霞等[5]对小尺度、微尺度和跨尺度3个层次的T型结构微通道内气液两相的相分流及相分离作用机制进行了分析总结,认为:分流特性主要受通道结构、入口流型、入口流速、工质物性等几个因素的影响,其中入口流型的影响效果明显;能够实现两相流真正分离的是跨尺度T型微通道,气液两相流分液的动力是界面运动及界面压差。Deshmukh等[6]最早提出压力驱动T型微混合器,采用集成的平面微泵,以阶跃函数产生脉动流诱导通道内流体扰动以增加接触面积,但需要多次脉冲才能实现液体混合。Ahmed等[7]提出一种马蹄形微通道结构设计,利用声波作用快速产生气泡以扰乱通道中的层流,从而实现了液体在微通道内高效混合。Hama等[8]在直型微通道的壁面上设置V形脊内构件,构成一种交错人字形的微混合器。模拟和实验对比发现,尽管流动处于层流状态,该微混合器可快速有效地实现流体混合。Tripathi等[9]在雷诺数Re=1~100范围内,对螺旋形微通道混合器内乙醇与水的混合特性及压降进行了数值模拟研究,并与蛇形及直形微通道混合器进行了比较。结果发现:在螺旋形及蛇形混合器中都会产生二次流涡旋并随雷诺数的增大而增强;Re=1时3种混合器的混合指数接近;螺旋形及蛇形微通道混合器的混合指数会随Re的增大先降后升、存在极低值,但均优于直形微通道混合器,而直形微通道混合器则呈单调下降趋势;Re=50时,螺旋形微通道混合器的混合指数比直形微通道混合器提高373%、比蛇形微通道混合器提高55.6%,在Re=100时则分别提高554.9%和17.3%;低雷诺数下3种混合器的压降几乎相同,高雷诺数下螺旋形及蛇形微通道混合器的压降仅略高于直形微通道混合器的压降。
国家“十三五”规划提出了优化能源结构,推进能源技术等能源战略任务,为生物柴油[10-11]技术发展提供了极好机遇。采用微通道反应器进行生物柴油合成具有反应控制精确性高、产品质量统一性好、传质效率高、反应快、副产物少和生产安全性高等优势[12]。但通过微型装置并行化来提高产量,实现在微通道反应器中连续合成生物柴油使其产量达到产业规模必须关注两个问题,即并行化反应器的流量分配与微通道内的混合性能。这些问题的解决都需要从微通道的结构着手,而采用数值模拟的手段进行微通道结构优化,则可显著缩短开发时间、减少项目成本[13-15]。
微通道技术的基础研究已取得长足进展,并在传热、传质与混合及分离方面获得了大量的应用。被动式微混合器常用的入口形式大多为T型、Y型等。除直型主通道外已有添加内构件以提高目标性能的大量研究,如立体多入口层流微混合器,通道折式Tesla型及C型微混合器,内嵌障碍物或挡板并将混合通道设计成蛇形、螺旋形、分流汇合型的弧形微混合器等。主动式微混合器则包括压力、声场、磁场、电场以及热场驱动式微混合器[16]。但对入口结构与主通道结构组合设计的研究报道则较少。现针对微通道反应器的混合问题,基于协同强化理念,利用多入口和障碍物构件组合设计一类雷诺数适用范围较广、混合性能较好的被动式组合结构微混合器,采用CFD(computational fluid dynamics)数值模拟研究操作参数和结构参数对新型微通道反应器混合性能的影响,以期为微通道合成生物柴油微反应器的设计提供理论基础。
1 几何模型
在反应器中可以通过流股细分提高物流间的接触面积以改善混合,同时在流股间通过构件干扰以速度扰动产生混沌涡流进而提供对流混合驱动力亦能有效改善体系的混合性能。基于组合强化理念,设计了一种含有入口段和内构件混合段的新型被动组合式微通道混合器,力求提高应用于生物柴油制备的微通道反应器中两种原料(即油与醇)的混合能力,其几何结构如图1所示。在图1所示的微混合器中,通道截面为深度H、宽W的矩形,相邻入口段距离为L1,入口段长度L2,入口段与主通道夹角α,通道内圆形阻块的直径为D,主通道长度为L。入口编号为1~7。具体参数模拟值如表1所示。
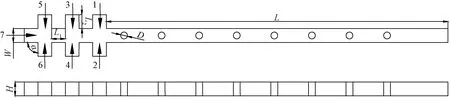
图1 微混合器几何结构示意图

表1 微通道结构初始模拟值
2 数值模拟
2.1 模型方程
常规尺度下的宏观流动,因为设备特征尺寸远大于其内部流体分子的平均自由程,其流动过程假定为连续性介质,进而推导出流体流动的三大主控方程,即基于质量守恒的连续性方程,基于能量守恒的能量方程和基于动量守恒的动量方程。研究表明,微流体属于微尺度范畴,其流动特征与常规尺寸下的宏观流动不同。这是因为微尺度下,流体流动受到尺度效应和粗糙度的影响。常规尺寸下的宏观流动中,表面张力效应、稀薄效应以及层流下小于5%的壁面粗糙度的影响可以忽略不计,而在微尺度下这些因素的影响表现的却尤为明显。另外,微尺度下流动空间小,流体分子与壁面没有足够的撞击频率,而产生一定速度的滑移,这与宏观流动的无滑移壁面边界不相同。通常,用来描述微流体流动的模型有两种:连续模型和分子模型。模型的适用范围与研究的尺度有关,可以用努森数kn(分子平均自由程和特征尺寸比)判别:①kn<10-2:流体流动满足Navier-Stokes(N-S)方程,采用速度无滑移壁面;②10-2
涉及的微流体属于微尺度范围中较大的数量级,研究微结构特征尺寸大于10-6m,特征尺寸远大于分子平均自由程,kn小于10-2。再考虑流体性质,微通道材料制成的壁面等因素,受到的微尺度效应影响较小,可忽略不计。因此,流体可做连续介质处理,按经典流体力学来求解分析其流体流动特征。即流体在微通道中处于不可压缩、稳态流动状态。其流动主控方程如下。
(1)连续性方程。对于不可压缩流体而言,基于质量守恒的连续性方程式为

(1)
式(1)中:u为流体速度,m/s;x、y、z为分量的方向。
(2)Navier-Stokes(N-S)动量方程。描述黏性不可压缩流体动量守恒的N-S方程在x、y和z3个方向上的展开式如式(2)~式(4)所示:

(2)
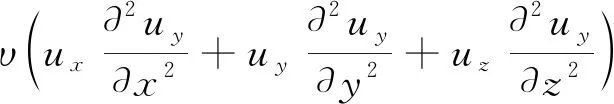
(3)
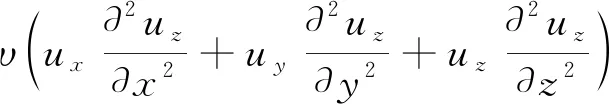
(4)
式中:ρ为流体密度,kg/m3;P为压力,Pa;υ为流体运动黏度,m2/s。
(3)对流扩散方程。混合过程中不同流体层间产生质量输运的对流扩散方程为

(5)
式(5)中:C为质量分数;D为流体间的扩散系数,m2/s。
2.2 求解设置
求解设置为三维双精度、非耦合隐式稳态;采用 SIMPLES(semi-implicit method for pressure linked equations)算法耦合压力与速度;空间离散格式采用二阶迎风;残差设置为10-5。
所研究的流体分子自由程远小于流体流动的特征尺寸,满足壁面无滑移,故微通道的壁面采用无滑移壁面边界条件。通道入口边界类型设置为速度入口,入口分别是纯油脂,纯醇进料,醇油进料量摩尔比为6∶1,其中油与醇的扩散系数使用Wilke-Chang方程[17]计算,结果为1.2×10-9m2/s,醇和油的物理性质如表2所示。出口边界类型设置成压力出口,出口压力值设为静压力P=0。

表2 流体物理性质
2.3 评价方法
通过归一化混合强度(MI)来评价流体流经微通道各截面的混合效果[5]。MI的定义为

(6)
式(6)中:σ为通道截面上的浓度标准差;σmax为通道截面浓度最强方差。
σ及σmax分别按式(7)和式(8)计算:
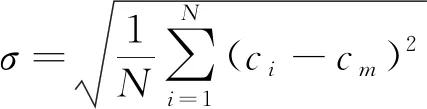
平泉市群山环绕,虽然为城市的综合绿化和生态环境的改善提供了必要的支撑,但城区内用地紧张,绿化用地不足,众多地区呈现绿地、绿带断层,绿地系统尚未形成完整的网络布局,不能充分发挥绿地的综合效益。
(7)
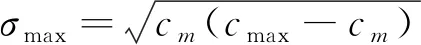
(8)
式中:Ci为截面上第i网格节点的浓度;Cm为截面上浓度的期望值;Cmax为截面上的最大浓度;N为截面上网格节点个数;MI为某通道截面处的混合强度,介于0~1,MI=0时表示无混合发生,MI=1时表示完全混合,MI越大混合效果越好。
2.4 有效性验证
对比Liu等[18]直通道微混合器混合性能研究的实验数据,以验证本文研究中模拟微通道内流体混合的计算有效性。与文献[18]中直通道微混合器结构参数相同的情况下,模拟考察了雷诺数对直通道微混合器混合性能的影响结果如图2所示。由图2可以看出,本文中模拟的结果与文献[18]结果趋势基本一致。增大流速提高雷诺数,混合程度变差。其中,雷诺数Re=5时,模拟结果与文献[18]中相差较大,但相对误差也仅是3.7%。所以本文研究中采用的数值模型、条件设置以及模拟结果都是合理有效的。

图2 文献值与模拟值对比
3 结果与讨论
3.1 入口角度对混合的影响
不同的入口角度,使流体经入口段进入主通道的速度方向不同,其对冲扰动程度不同,同时不同入口角度还会使流体相遇的接触面大小也不同。因此,入口角度对流体在微通道中的混合产生影响。保持其他结构参数一致,雷诺数为0.1条件下分别对0°、30°、60°、90°的入口角度进行混合模拟,结果如图3~图5所示。
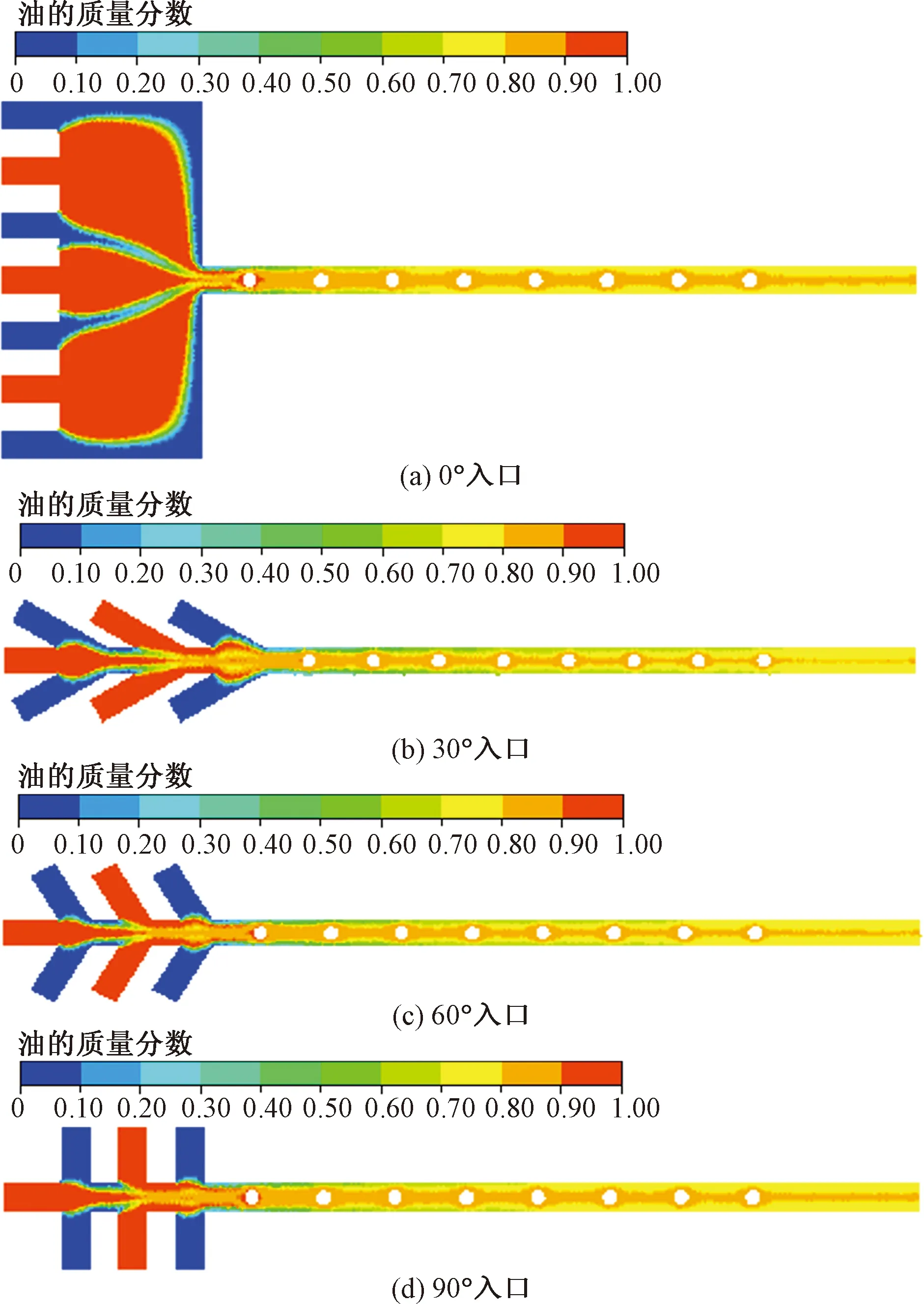
图3 不同角度入口段油质量分数云图
由图3可以看出,不同角度的入口段中流体交汇处产生的扰动程度不同。0°入口段物料自入口至混合通道间有明显的分区,汇入主通道时层间的接触面积很小;60°与90°入口段结构在逐次汇入主通道时物料层间彼此叠压扰动并发生扩散混合作用,但层间接触长度仍然较小,分别为宽度的1.15倍和1倍;而30°的入口段结构,在7个入口全部汇入主通道前,彼此层间的接触长度为入口宽度的2倍,其扰动混合作用最大。由图4和图5看出入口角度为30°时,在主通道的入口附近,其混合强度就已经达到0.70,而在通道出口截面上的混合强度则可达0.914,分别高出0°设计的7.46%,90°设计的5.25%。
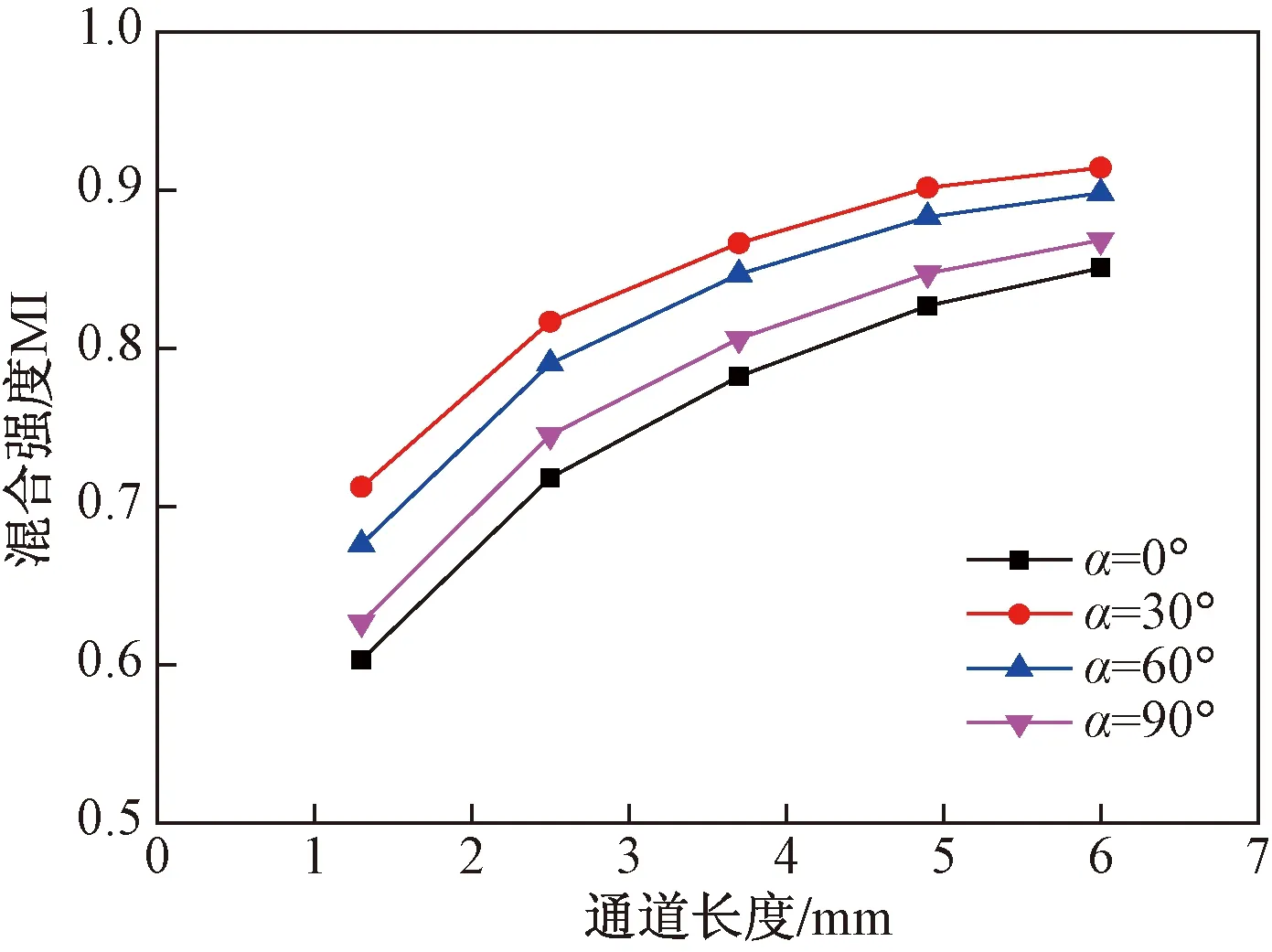
图4 各截面处的混合强度曲线
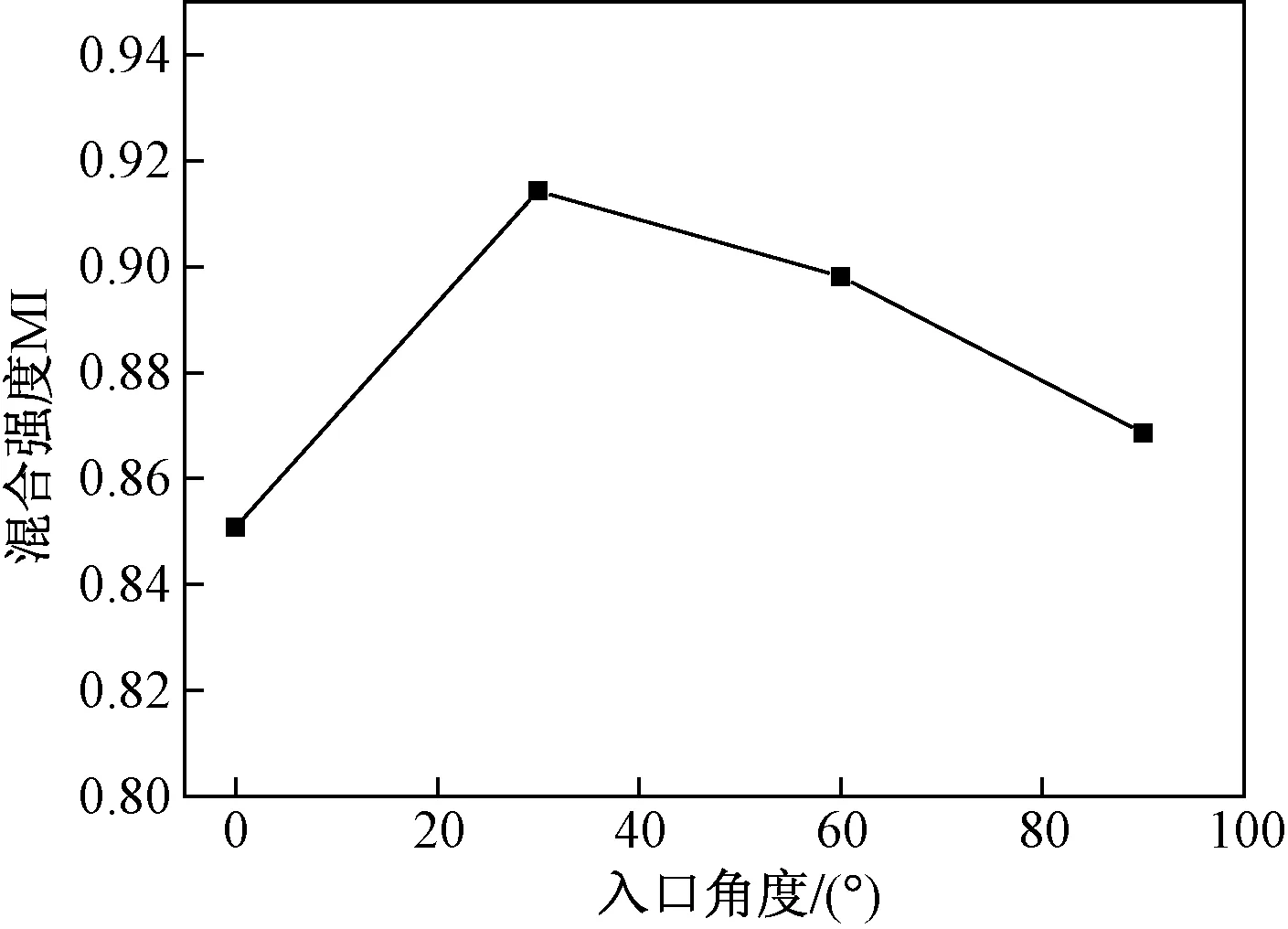
图5 混合强度随入口角度变化曲线
图6为不同角度下主通道上的压力损失变化曲线,虽然30°入口角度下的压力消耗最大,但只比压力消耗最小的0°入口设计高出2.38%,而混合强度提升则了7.46%,显然是有效的。

图6 压降随入口角度的变化曲线
3.2 组合式内构件对混合的影响
3.2.1 几何模型

图7 新型组合式微通道平面示意图
3.2.2 组合式微通道流动特性分析
图8为Re等于0.1及100时通道内局部速度矢量图。由8图可以看出Re=0.1时,通道内无明显涡流,而Re=100时构件前后则产生了明显涡流。这表明Re=0.1时,流体在通道内呈层流流动,混合主要依靠分子扩散作用;Re=100时,流体在通道内受构件的影响,由无旋涡流变为有局部旋涡流,随着局部涡流的出现,打破了本来的层流流动状态,混沌性增强,对流扩散混合作用增强。
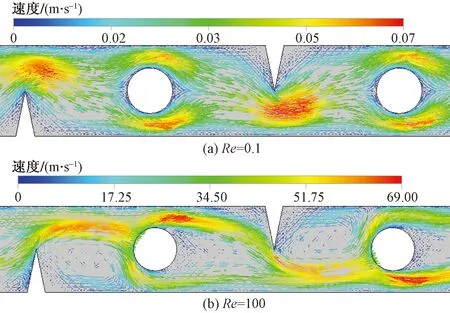
图8 混合单元内速度矢量图
图9为沿流动X方向在X=2.2 mm处截面上的X向速度分量结果。由图9(a)可以看出:Re为0.1和1时,流体全部沿X正方向流动且Re=1时流动速度大于Re=0.1的。由图9(b)可见,当Re为10和50时,出现局部流体沿X负方向运动,这就是涡流产生的标志;当Re增大时,涡流扰动越明显,涡的产生可以提高传质效果,但也会引起局部阻力增大。因此对于微通道的结构设计,在考虑涡流对流增强扩散作用的同时,需要尽可能地避免不必要的压力损失。
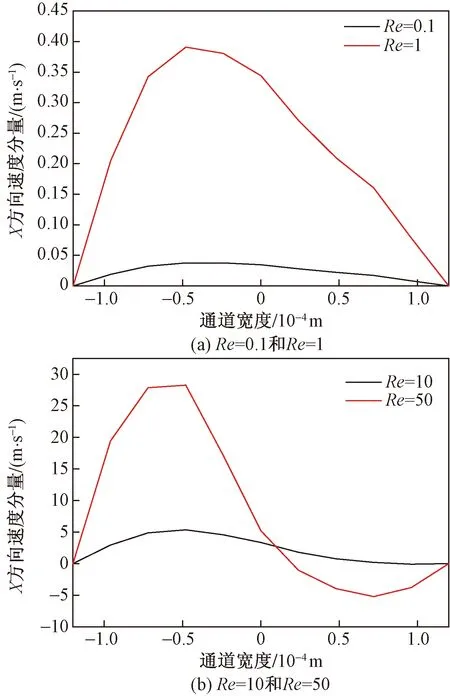
图9 不同雷诺数下X=2.2 mm截面中心线上流体X方向速度分量
3.2.3 圆形阻块构件直径的影响
在保持其他结构参数不变的情况下,通过对不同直径D圆形阻块构件的组合式微混合器的模拟计算,分析其直径D在不同雷诺数下对混合性能的影响,得到的结果如图10所示。
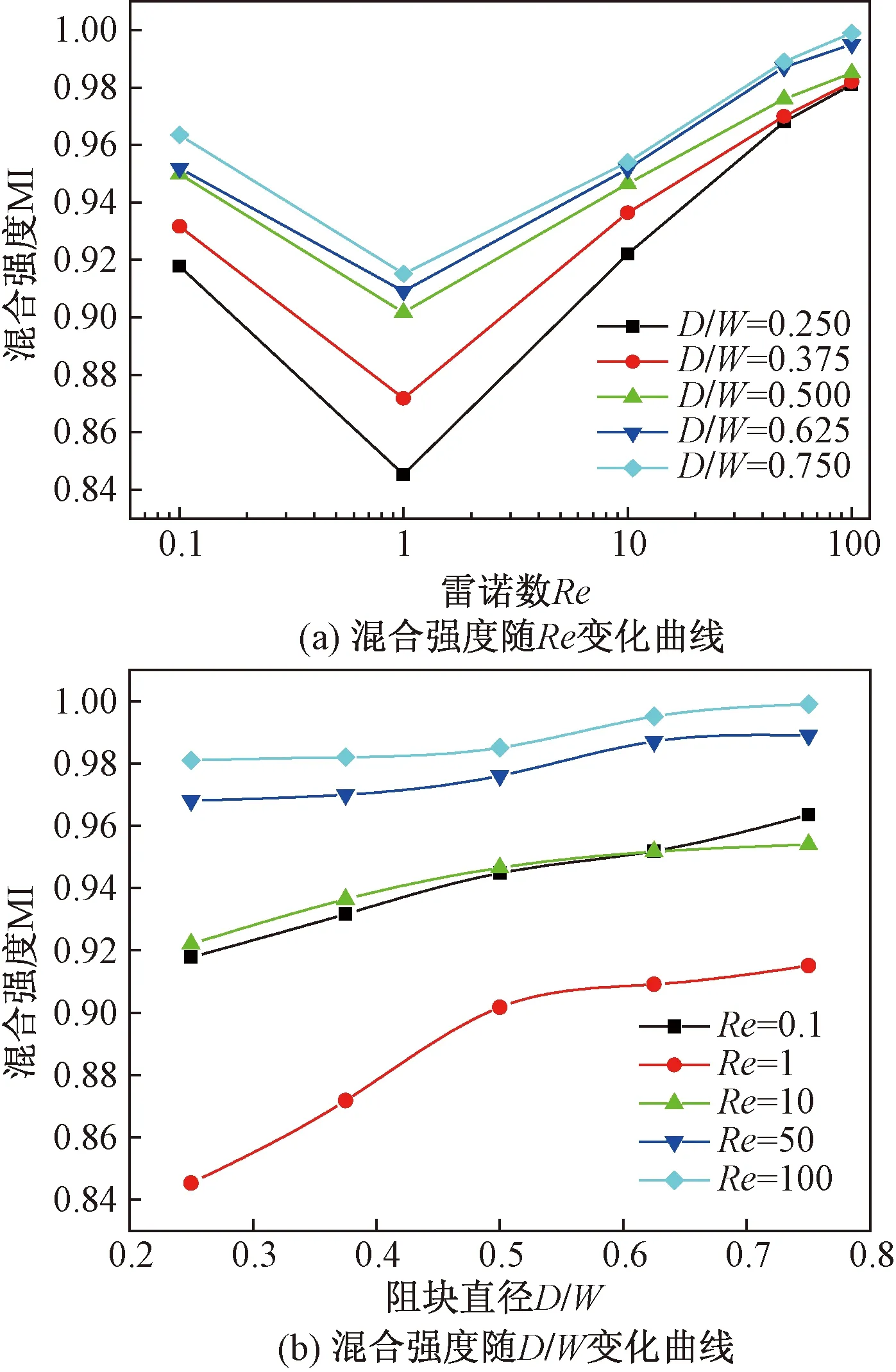
图10 混合强度随Re及D/W变化曲线
图10(a)为不同直径D下的微通道混合效率随雷诺数 (0.1
图11为不同阻块直径D下的微通道的压力损失曲线。由图11可知,微通道进出口压降的总变化趋势是随着雷诺数的增加而增大的。当D/W=0.25~0.5)(D=60、90、120 μm)时,相同Re条件下,压降增幅不明显,但当D大于120 μm继续增加时,压降增幅加大。综合压降和混合强度的变化,可见最佳圆形阻块直径为D/W=0.5(D=120 μm)。

图11 不同D/W下微通道压降曲线
3.2.4 三角挡板构件高度的影响
在其他结构参数不变的条件下,改变三角形挡板构件的高度H1,考察微通道混合强度随雷诺数Re的变化曲线,结果如图12所示。由图12可见,随着H1的不断增大,混合效果改善,H1=0(无挡板)条件下,在Re=10时处的混合强度最低仅为0.754,而其他几种挡板高度下,混合强度最低点在Re=1处。这是由于H1=0时,无三角挡板,流体只能依靠圆形组块构件产生混沌流强化混合,产生涡流所需雷诺数较大。图12(b)是不同雷诺数下混合效率随H1变化的曲线。由图12(b)可以看出,Re为1、10和50时,混合强度对H1变化敏感,H1增大时,混合强度增大明显。但Re为0.1和100时,H1的变化对混合强度影响较弱,这是由于Re=0.1时流速小,流体在微通道停留时间长,混合由扩散作用主导;当Re=100时流速足够大,在含有圆形阻块构件的主通道内足以形成涡流强化混合。由图12(b)还发现,H1/W>0.5(H1>120 μm)混合强度曲线保持平稳,因此120 μm的挡板高度即可满足流体混合要求。图13为不同挡板高度H1下的微通道压降曲线,由图13知在Re=0.1~10范围内,压降不随H1/W而变;但Re=50~100范围内,H1/W>1/3时压降开始增大,Re=100时增大尤为明显。考虑混合效率和压降损失,确定H1/W=1/2即H1=120 μm为优化的三角形挡板高度。
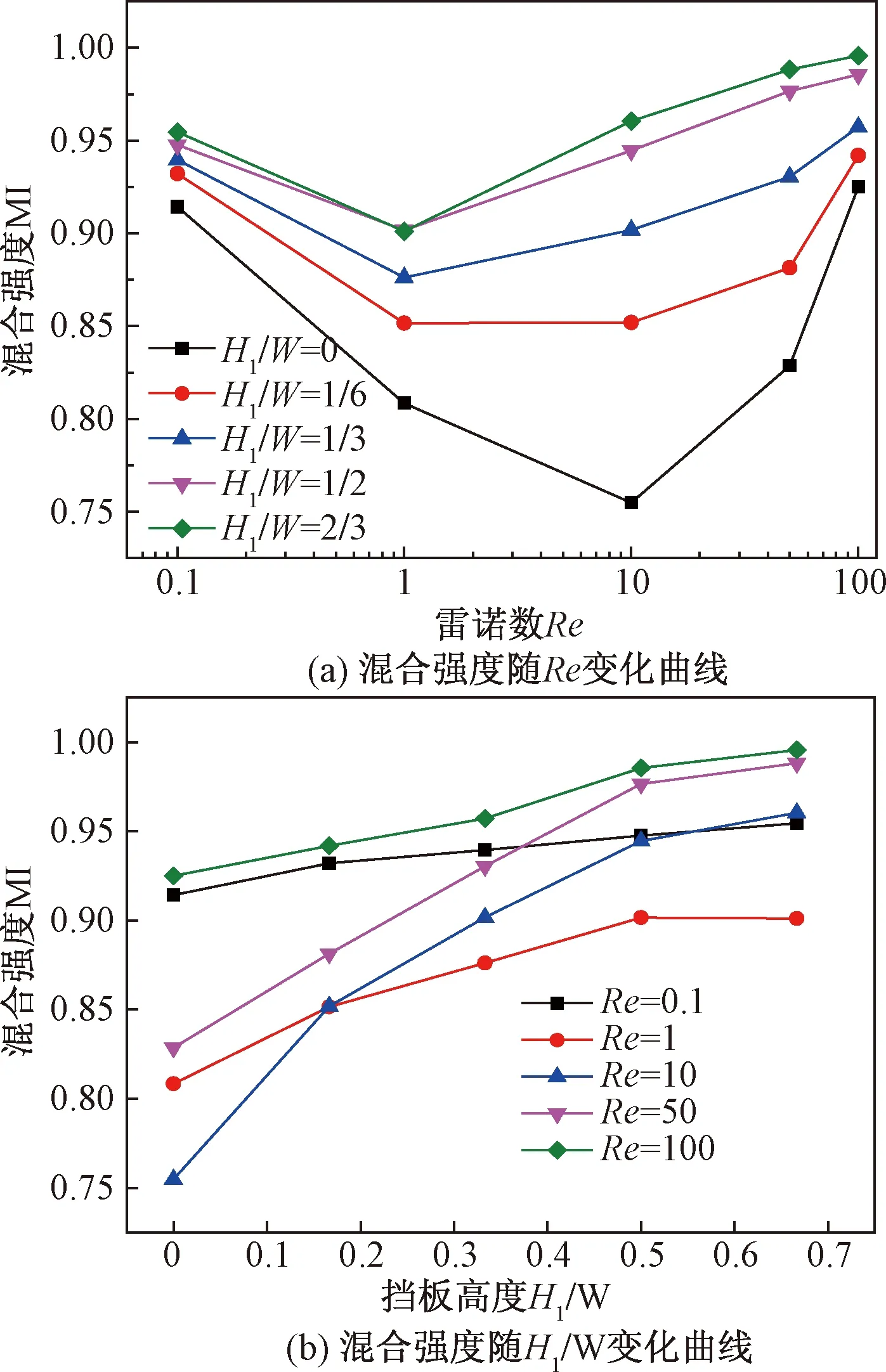
图12 混合强度随Re及H1/W变化曲线

图13 不同H1/W下微通道压降曲线
3.2.5 内构件间距的影响
考察三角形挡板与圆形阻块构件间距P对混合产生的影响,其P分别为240、270、300、330和360 μm,得到的模拟结果如图14~图15所示。图14(a)为不同P/W下混合强度随Re的变化曲线。由图14(a)可以看出,P/W=1.25~1.375(P=300和330 μm,即P/W=5/4~11/8)时,在0.1 图14 混合强度随Re及P/W的变化曲线 图15 不同P/W下微通道的压降曲线 物料在微通道内所达到的混合强度与微通道的长度有关,其结果如图16所示。由图16可以看出,新型组合式微通道出口处的混合强度在所考察的雷诺数范围内都保持在0.9以上,这得益于通道入口段基于增强扩散混合理念的多层设计。混合强度相对较低的雷诺数为Re=1,这可能是流体在微通道停留时间相对Re=0.1时较短且通道内并无混沌对流的原因。Re>10时,微通道的出口混合强度达0.937以上,这得益于圆形阻块和三角挡板构件的组合设计,能在通道内产生局部涡流,通过混沌对流强化混合。不同雷诺数下流体混合强度在主通道长度2.5 mm之前均增长较快,长度在 4.9 mm 之后混合强度增长缓慢。一般地,混合效率达到0.95即可认为流体已达到完全混合状态,此条件可在Re≤0.1和Re≥20范围得到满足,如若生产中对混合强度的要求不苛刻,混合强度达到0.9以上即可,那么新型组合式微通道在所研究的Re=0.1~100范围内都可以满足,即有较大的操作弹性范围。 图16 混合强度沿通道长度变化曲线 设定醇油摩尔比为6∶1~12∶1进行数值模拟,考察物料含量对混合的影响,设定醇油摩尔比下油的质量分数依次为:0.760 8、0.731 6、0.704 6、0.679 5、0.656 2、0.634 4和0.614 0,得到如图17所示的微通道出口混合强度变化曲线。由图17可知,混合强度随着摩尔比的增大而变差。其中Re=0.1时混合强度受摩尔比变化的影响较大、Re=100的影响较小;随着雷诺数的增大,醇油摩尔比对混合强度的影响逐渐减弱。由此可见,醇油摩尔比不同应选取适宜的Re范围,以满足醇油的混合效果。 图17 混合强度随摩尔比变化曲线 基于协同组合理念,提出了一种新型组合式微通道。模拟了微混合器入口段结构对流动与混合的影响,并探讨了通道内组合构件设置对混合性能的强化作用,优化了微通道混合器的结构尺寸。研究结果表明,在微通道入口段设置多入口可以增加物料间的对冲扰动、缩短扩散距离,改变入口角度能增加物料间的接触面积,优化得到的入口角度为30°。在混合段引入三角形挡板和圆形阻块组合内构件,可以在构件前后的流体层间产生混沌涡流,提供对流混合动力。在挡板高度120 μm、形阻块直径120 μm、构件间距330 μm、混合段长度6 mm的适宜结构下,雷诺数0.1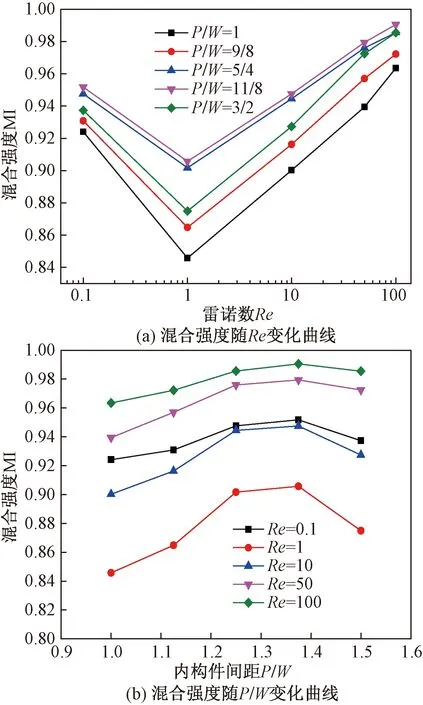
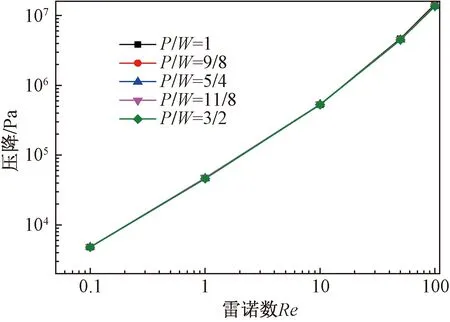
3.3 通道长度对混合的影响

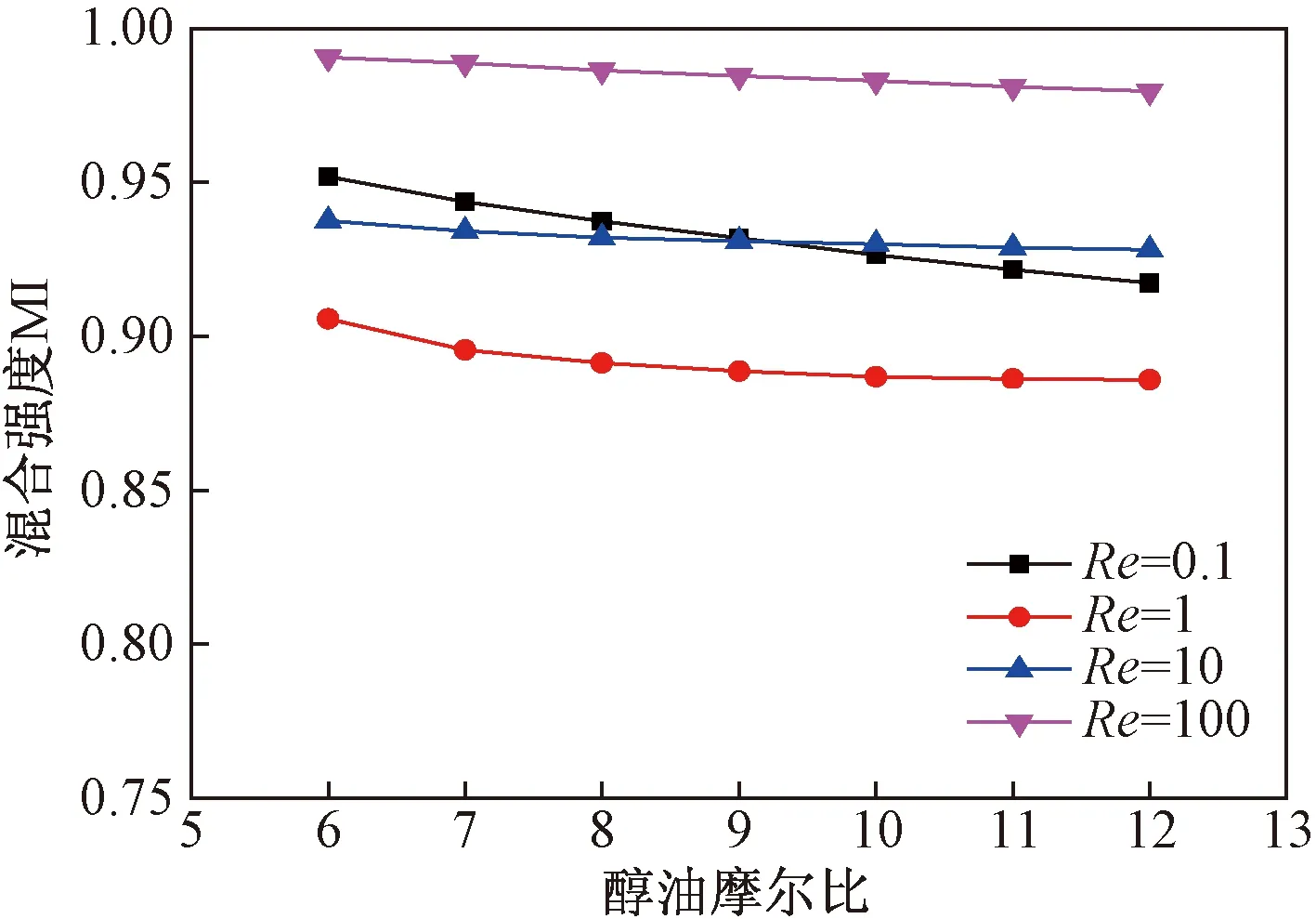
3.4 醇油摩尔比对混合影响
4 结论

