抗浮锚杆荷载-位移特性及极限承载力预测

井德胜， 白晓宇*， 刘 超，2， 刘永江， 张明义， 黄永峰

(1.青岛理工大学土木工程学院， 青岛 266033； 2.青岛市建筑材料研究所有限公司， 青岛 266044；3.青岛大港海关， 青岛 266011)

随着地下空间的开发与利用，基础埋深不断加大，地下结构抗浮问题日益突出。目前，常见的抗浮措施有压重法、加厚基础底板、降排地下水等，虽然都能达到预期的效果，但从经济和环境效益上看，混凝土消耗量过大，不利于工程成本管控[1]。抗拔桩也是抗浮工程中常用的抗浮措施，因其具有直径较大、承载力高、桩间距大等特点，容易产生应力集中现象，极易造成基础底板局部开裂。为防止此类问题，常通过增加底板厚度，从而导致成本增加，效益不佳。近年来，抗浮锚杆因其布置灵活、单点受力小、工艺简单、成本较低等优势被大力推广[2-3]。而面对复杂的地下环境，包括地下水腐蚀、杂散电流等电化学腐蚀，钢筋抗浮锚杆始终难以从根本上解决耐腐蚀性问题，遂有“定时炸弹”之说[4]。

玻璃纤维增强聚合物(glass fiber reinforced polymer，GFRP)用作非金属抗浮锚杆，它是将浸泡于由环氧树脂等合成树脂组成的基体材料中的玻璃纤维丝，经多次高温连续拉挤工艺及促进剂和固化剂处理后形成的一种新型复合材料筋材[5]。因其轻质高强，耐腐蚀性能好，绿色环保等优势被认为是金属锚杆的良好替代品，并在许多工程应用中得到成功验证[6-7]。Zheng等[8]对不同规格的GFRP筋经室内拉拔试验得出其抗拉强度平均值为799 MPa，是同规格热轧带肋钢筋的2倍。Altalmas等[9]通过将GFRP筋材浸入酸、碱、盐等腐蚀环境30 d，电镜扫描下，其杆体表面保存较完好，且强度保证率达到90%。Soong等[10]和李国维等[11]发现：纤维增强聚合物锚杆与水泥基材料的热膨胀系数相近，其共同作用时变形较一致且协调性较好。白晓宇等[12-14]、李国维等[15-16]在风化岩地层中进行现场拉拔破坏性试验及蠕变试验，分析了GFRP抗浮锚杆作用机理。目前，现行的国家规范中缺乏非金属抗浮锚杆的设计标准及检验规程，而针对锚杆的荷载-位移曲线研究可以直观的表现锚杆的实际受力与位移情况，有利推动国家相关标准的出台。陈建功等[17]利用小波函数，推导出荷载-位移曲线函数，与工程实测数据拟合度较高。崔强等[18]通过强风化岩层中抗拔桩拉拔试验，采用双曲线模型得出无量纲荷载(Q/QL2)与上拔位移(s)之间的关系曲线，对比实测值认为模型预测结果较好。

基于此，根据青岛市崂山区某基坑抗浮工程，对GFRP和钢筋抗浮锚杆进行现场拉拔破坏性试验。分析其承载力、变形及第一界面(锚杆-锚固体界面)相对滑移特性。通过绘制出的荷载-位移曲线，利用多项式拟合预测极限承载力，以期对同类型抗浮锚杆设计及检测提供借鉴和思考。

1 试验方案

1.1 工程地质概况

试验场地位于青岛市崂山区某在建建筑基坑工程中。崂山区主要由构造侵蚀地貌、构造剥蚀地貌和堆积地貌组成，且其在高度上依次呈中低山、丘陵、滨海平原及山间谷地阶梯状分布。场区内地质构造复杂，岩层埋深不均(3.2～18.3 m)，岩性参差不齐，基岩主要为中风化花岗岩，呈红褐色，裂隙面大部分变色，敲击声清脆且有回弹，地下水位分布在1.8～8.3 m。基坑岩层主要物理力学指标如表1所示。

表1 岩层主要物理力学指标

1.2 试验锚杆参数

本试验所取锚杆为等直径、等长度的GFRP锚杆和钢筋锚杆。其中GFRP是选自南京某公司生产的表面黏砂型抗浮锚杆，其是以环氧树脂为基体(约占25%)，玻璃纤维为骨架(约占75%)，经拉挤、缠绕、固化形成。钢筋锚杆选取三级螺纹钢筋，直径28 mm。经过样品检验，所取试验锚杆主要物理力学指标参数由生产厂家提供，如表2所示。试验锚杆共6根，其主要设计参数如表3所示。

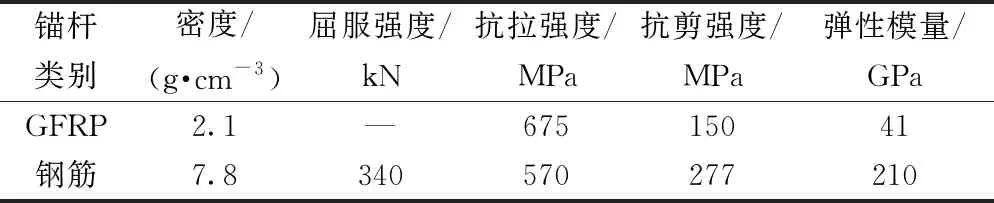
表2 GFRP与钢筋锚杆主要物理力学指标参数

表3 主要设计参数

1.3 试验过程及加载方式

试验场地清表，钻机定位后，利用钻机垂直开孔取芯5 m。试验锚杆间距保持3 m。利用定位对中器将锚杆放置在设计标高。本试验采用M30水泥砂浆，设计养护期结束后，经检测，28 d平均抗压强度为34.1 MPa。

试验使用本团队自主创新研制的加载装置，为了防止锚杆夹持端受力破坏，试验中采用钢套管内嵌结构胶进行固定和保护。本装置最大拉拔力为1 000 kN，能够满足试验需要。位移检测百分表量程为30 mm，精确度为0.01 mm。加载装置从下到上依次安装完成后，严格按照《抗浮锚杆技术规程》(YB/T4659—2018)[19]等相关规范进行加载。试验采用逐级加载方式，以每级40 kN逐级匀速加载，加载时长控制在5～8 s，相邻2级荷载稳压15 min，直至锚杆发生破坏。需要注意的是，每级加载结束后应及时采集数据，稳压期间每5 min测读一次数据并记录。图1为试验过程。

图1 试验过程

试验过程中，假设锚杆杆体水平剖面上各点竖直位移量相等，为了便于测量，取外表面作为杆体位移。在对锚固体位移量的测量中，由于锚固体面积较大，选取锚固体中部界面顶部位移作为锚固体位移量。

2 试验结果与分析

2.1 破坏荷载及位移特征

试验过程中，锚杆的破坏分为拔断破坏和剪切-滑移破坏。钢筋锚杆发生拔断破坏时，杆体突然“嘣”的一声巨响发生断裂，且断口较为平整，如试验锚杆Steel-02和Steel-03；GFRP锚杆发生拔断破坏时，杆体根部出现纤维丝剥离现象，如试验锚杆GFRP-01和GFRP-03。依据规范[19]，当杆体与锚固体发生剪切-滑移破坏时，锚杆杆体位移不收敛，位移量大于前一级荷载作用下的5倍或者锚杆杆体总位移量超过设计允许值时，如试验锚杆GFRP-02和Steel-01。

试验锚杆极限状态特征参数如表4所示。由表4可以看出，钢筋锚杆与GFRP锚杆平均破坏荷载分别为324 kN、394 kN，均小于其极限拉拔承载力351 kN、416 kN，强度利用率均达到92%。其中发生拔断破坏的锚杆，其强度利用率高于发生其他破坏形式的锚杆，其中GFRP-02、Steel-01破坏荷载较小。究其原因，可能是由于锚杆施工过程中，锚固体强度不均匀、杆体与锚固体之间局部黏结不紧密、岩土层物理力学性质存在微小差异，导致锚杆杆体与锚固体之间的黏结强度不同。试验过程中出现的杆体与锚固体之间存在位移差值，是因为当杆体达到极限状态时，杆体受力状态下出现弹、塑性变形被拉长以及锚固界面间发生相对滑移，导致杆体与锚固体的位移存在一定差值。而GFRP-02、Steel-01与同材质锚杆相比，锚杆、锚固体相对位移较大。由于钢筋弹性模量较GFRP筋高达5倍，则整体钢筋锚杆相对位移更大。如果钢筋、GFRP筋锚杆均按等截面计算，钢筋锚杆内锚固段平均黏结强度为0.82 MPa，GFRP锚杆为1.00 MPa。本试验灌浆体采用M30水泥砂浆，《抗浮锚杆技术规程》(YB/T4659—2018)[19]的规定，满足设计要求。

表4 试验锚杆极限状态特征参数

图2为试验锚杆荷载-位移曲线。钢筋锚杆在均匀加载过程中，位移会发生突变。将钢筋锚杆加载至240 kN后，杆体的位移迅速增加，分析认为，此时杆体与锚固体界面黏结力难以承受荷载，发生相对滑移以平衡拉拔力。而GFRP锚杆变化趋势较均匀，呈线性增加。前、中期，由于两种材质的弹性模量不同，在相同荷载作用下，GFRP锚杆杆体的位移均比钢筋锚杆大。

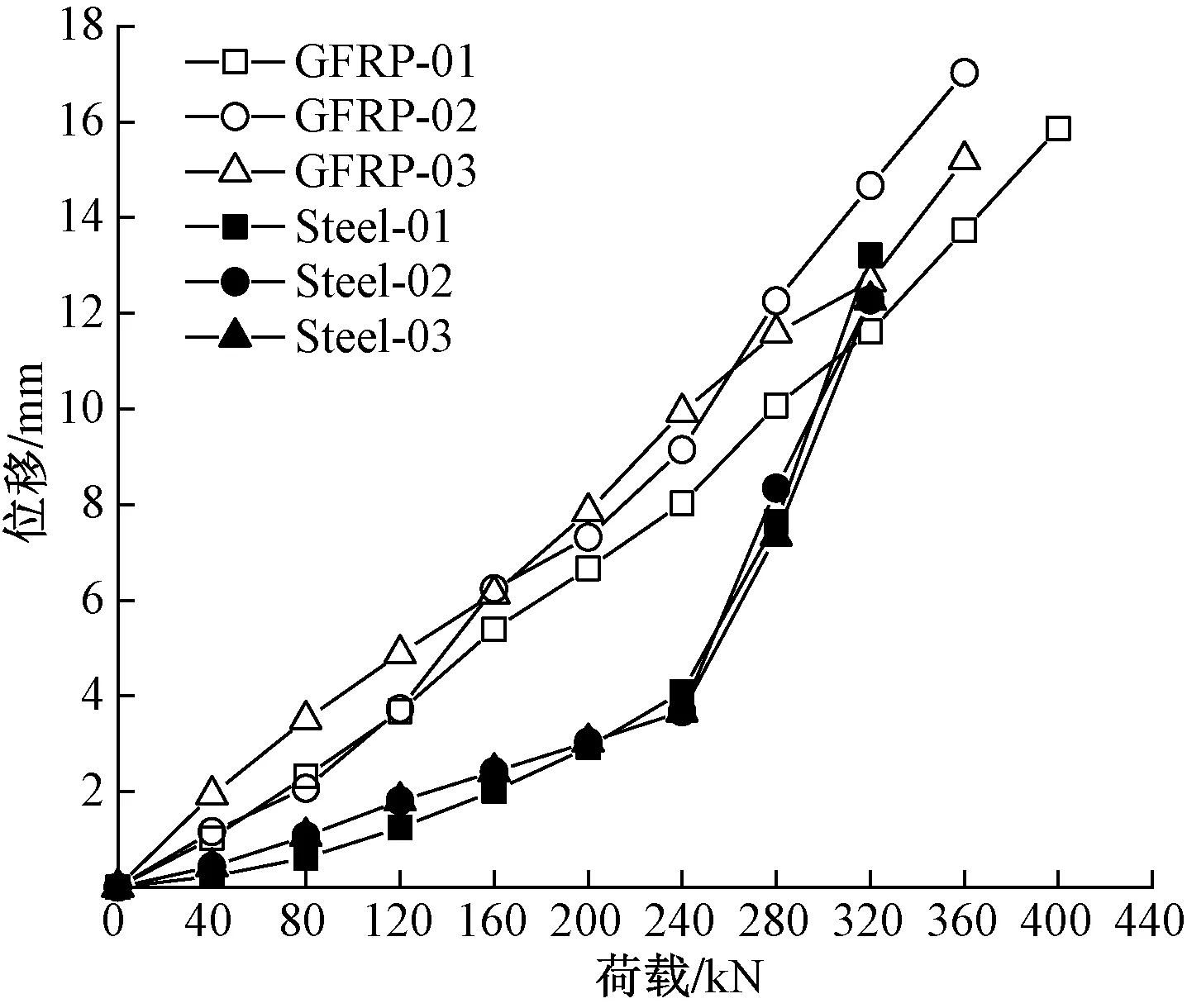
图2 荷载-位移曲线

综上所述，在相同直径、相同锚固长度条件下，GFRP锚杆承受了更大的拉拔力，能够发挥更大的黏结强度。试验过程中，GFRP筋和钢筋都出现了拔断破坏和剪切-滑移破坏，且GFRP筋锚杆杆体的位移要大于钢筋锚杆。这与李国维等[15]的研究结果相似。据此可验证，实际工程中，同规格GFRP锚杆比钢筋锚杆更可靠。据此可推测：可以使用直径较小的GFRP锚杆替代较大的直径钢筋锚杆。

2.2 锚杆-锚固体相对滑移特性

非金属抗浮锚杆与锚固体间类似钢塑连接，且界面凹凸不平，又因其黏结作用力影响因素多，隐蔽性强等特点，给研究带来了很多阻力。在现场拉拔检测中，时常会出现杆体-锚固体相对滑移现象。而杆体-锚固体界面黏结力主要由其界面相互间的化学黏着力、摩擦力、机械咬合力提供。本试验杆体-锚固体相对滑移量S可据式(1)计算：

S=(S杆-S杆弹)-(S锚-S锚弹)

(1)

式(1)中：S杆为试验杆体位移，mm；S杆弹为锚固段杆体的弹性形变量，mm；S锚为试验锚固体位移，mm；S锚弹为锚固体弹性形变量，mm。

试验中，将位移计安装在自由端根部，锚杆与锚固体弹性模量较小，其弹性形变量在这里不做考虑。根据式(1)对拉拔过程各级荷载作用下，其相对滑移量的计算结果如图3所示。

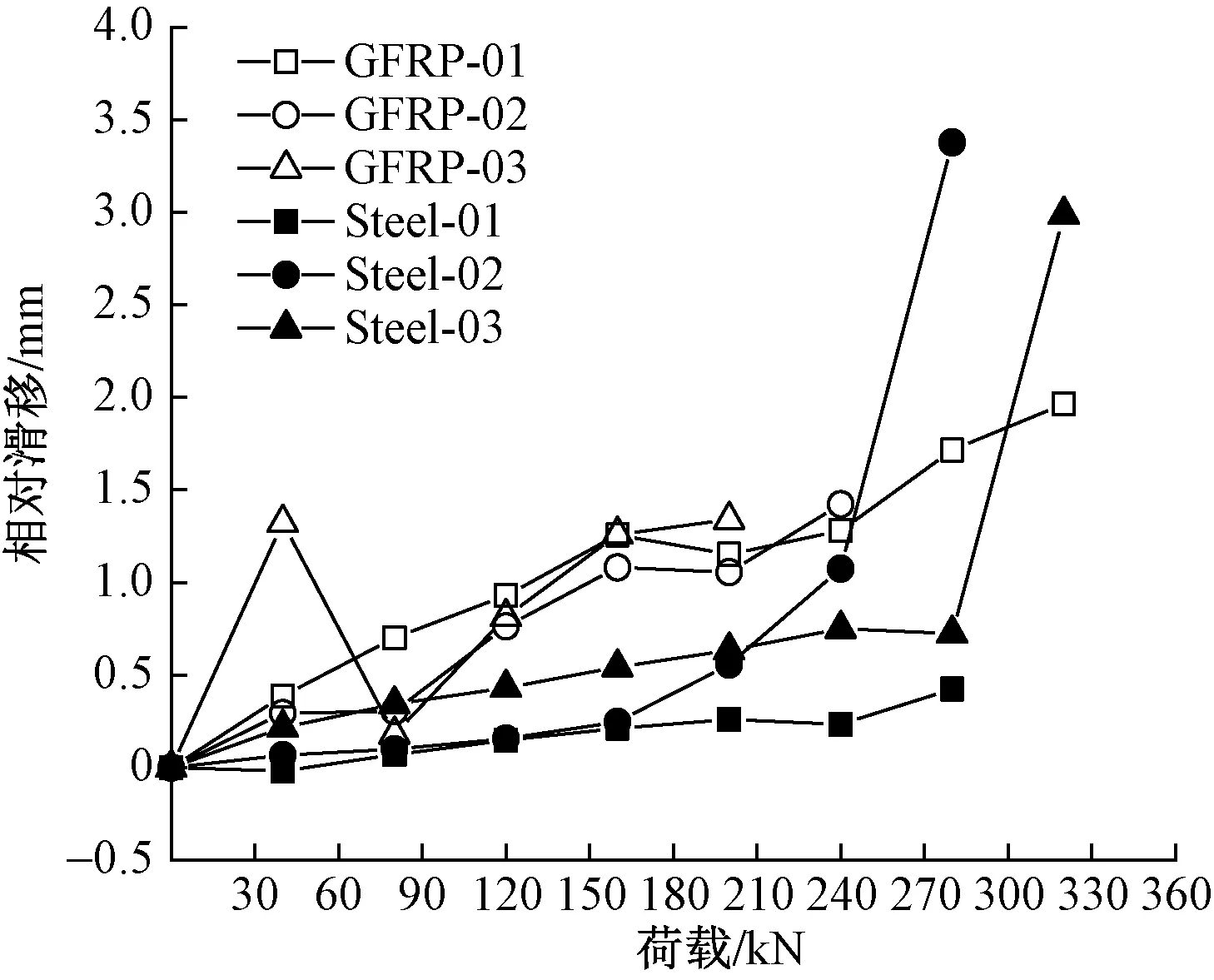
图3 试验锚杆杆体与锚固体界面相对滑移随荷载变化曲线

由图3可知，钢筋锚杆最终相对滑移量明显高于GFRP抗浮锚杆，体现了GFRP锚杆与砂浆之间的黏结性能更好。GFRP锚杆在拉拔前中期的相对滑移量大于钢筋锚杆，且整体呈缓S形。究其原因，早期随着拉拔力增大，锚杆-锚固体界面黏结面积随之增大，其界面化学黏结力与摩擦力逐渐增大，杆体滑移早于锚固体。当荷载达到150～210 kN时曲线变缓且略有下降，此时锚杆与锚固体间机械咬合力开始发挥作用，随着锚杆的上拔，锚固体也随之同步上移。当荷载达到240 kN后，相对滑移量加速增大直至破坏，此时随着机械咬合力的增大，难以承担拉拔荷载，第一界面黏结力逐渐小于第二界面。而钢筋锚杆前中期发展大体呈线性增加，整体呈L形。在240～270 kN期间，钢筋达到屈服强度，随着荷载的增加，相对位移量出现明显增大直至发生破坏。如图3所示，GFRP-03在荷载水平为60 kN后，锚杆杆体与锚固体的相对滑移出现迅速减小的情况。分析认为，主要是由于施加第二级荷载(80 kN)时，锚固体顶面出现起皮现象，导致锚固体的位移的异常，锚杆杆体与锚固体出现相对滑移，且在第二级荷载之后，相对滑移的变化趋势与其他试验锚杆一致。综上所述，GFRP抗浮锚杆与钢筋锚杆相比，变形发展较平稳，更贴合实际工程应用。

3 抗浮锚杆极限承载力预测

3.1 多项式拟合分析

荷载-位移曲线可以集中体现抗浮锚杆在受荷作用下承载力和位移的变化形态，可以直接得出极限承载力和极限位移量。但在实际工程中难以将工程锚杆做到极限破坏，这对GFRP抗浮锚杆实际工程应用的研究带来了阻力。而利用数学方法拟合曲线特性，精准预测不同条件下的荷载-位移变化规律可以解决这一难题。根据目前《建筑工程抗浮技术标准》(JGJ 476—2019)[20]、《锚杆锚固质量无损检测技术规程》(JGJ/T 182—2009)[21]等相关规范规定：抗浮锚杆张拉检测数量不得低于总数的10%且每检验批不得低于20根。目前使用的数学方法有多项式模型、双曲线模型、指数模型、幂函数模型等。根据本试验荷载-位移曲线(图2)，接近二次多项式函数分布。

经二次多项式回归拟合，GFRP-01、GFRP-02、GFRP-03抗浮锚杆Q-s的回归方程为

(2)

(3)

(4)

式中：Q1、Q2、Q3分别为GFRP-01、GFRP-02、GFRP-03抗浮锚杆承载力拟合值，kN；s为杆体位移，mm；R为相关系数。

图4为锚杆荷载-位移曲线拟合曲线图。将上述方程拟合得出承载力预测方程，如图5、式(5)所示。其承载力预测精度高于92%，如表5所示。

表5 GFRP抗浮锚杆极限承载力预测结果

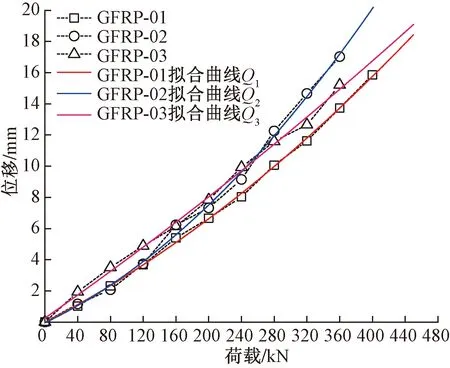
图4 GFRP抗浮锚杆荷载-位移曲线拟合

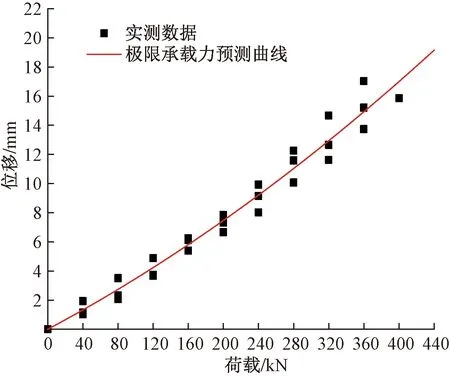
图5 极限承载力预测

s=2.587 77×10-5Q2+0.032 15Q，R2=0.991 0

(5)

式(5)中：Q为GFRP抗浮锚杆承载力预测值，kN。

3.2 工程案例验证

案例一根据文献[22]，某基坑抗浮工程中，在中风化花岗岩地质条件下，对直径28 mm的GFRP抗浮锚杆进行现场拉拔试验，以其中G28-01、G28-02、G28-03锚杆为例进行验证，如图6所示。

图6 案例一：极限承载力预测图

案例二根据文献[23]，针对不同砂浆约束条件对GFRP土钉拔出性能的影响进行了室内试验研究，其荷载-位移曲线和极限承载力预测如图7所示。

图7 案例二：极限承载力预测图

根据以上两个案例，如表6所示，可以得出极限承载力预测值的精度平均为81.8%，且随着锚杆杆体最终位移量越小，其预测结果越理想，最高达到96.15%，基本达到预测的目的。但当锚杆杆体位移量大于20 mm时，拟合效果不佳，需要进一步优化方程。

表6 极限承载力预测分析

4 结论

(1)通过对6组同规格的GFRP抗浮锚杆及钢筋抗浮锚杆进行现场拉拔破坏性试验，钢筋锚杆和GFRP锚杆均出现拔断破坏和剪切-滑移破坏，而GFRP抗浮锚杆承载力均大于钢筋锚杆。因此，较小直径的GFRP锚杆可以替代较大直径的钢筋锚杆。

(2)对比其荷载-位移曲线可知，GFRP锚杆位移随荷载稳定增长，而钢筋锚杆加载中后期，出现陡坡段。钢筋锚杆内锚固段黏结强度均值为0.82 MPa，GFRP锚杆均值为1.00 MPa。GFRP抗浮锚杆较于钢筋锚杆，更贴合实际工程应用。

(3)在对锚杆-锚固体相对滑移量分析中，GFRP抗浮锚杆相对滑移量随荷载增加较稳定，整体呈缓S形。而对于钢筋锚杆，当荷载达到屈服强度时，相对位移突然增大，整体呈L形。

(4)根据试验锚杆荷载-位移曲线特性，利用二次多项式回归拟合推导承载力预测方程，承载力预测精度最高达到95%。经过案例再论证，认为对于锚杆杆体位移量小于20 mm时，预测效果较好，最高达到96.15%。对工程应用有借鉴和参考价值。