基于双边匹配的多属性共享停车匹配研究

贾富强，李引珍，马昌喜，代存杰

(兰州交通大学 交通运输学院，兰州 730070)

随着社会经济的快速发展和汽车保有量的飞速增长，大多数城市停车困难现象十分普遍，严重制约了社会经济的发展和人们的正常出行和日常生活.所谓停车泊位共享[1]指的是在一定的区域内，根据不同用户对于停车泊位使用时间的差异性，采取共同使用停车泊位的组织方式.如何合理利用白天居住区空闲车位和晚上商业区空闲车位进行共享停车[2]，可以提高车位利用率并且有效缓解交通拥堵.

在共享停车实施过程中，最核心的问题是出行者停车选择行为和共享停车位的分配.He等[3]通过对不同停车目的共享停车位选择进行研究得到出行距离和费用对不同停车目的停车行为选择影响不同.Ding等[4]利用加权topsis模型确定考虑出行路径和出行时间的最优停车位匹配问题.Hu等[5]通过对比研究得到行距离、停车时间与停车费等因素直接影响共享停车选择.郑竞恒[6]考虑停车收费、步行距离及停车方式对不同类型停车目的下停车行为的影响.杨晓芳等[7]对停车费率差、步行距离等因素对驾驶员停车行为的影响进行了研究.王健等[8]对多指标多原因的停车选择行为进行了实证性研究.段满珍等[9]对居住区共享车位分配问题进行了研究.陈峻等[10]利用时空消耗模型对片区组合停车设施的共享车位匹配问题进行了研究.陈峻等[11]对中心城区高校停车泊位共享问题进行研究.张文会等[12]从停车需求、平均步行距离等方面对居住区共享停车泊位利用率的提升问题进行了研究.文献[13-14]从出行成本入手研究了出行者和停车场管理者之间的博弈来研究共享停车位效果.姚恩建等[15]以提高共享停车位泊位利用率为目标，研究了不停时段和需求下停车位匹配问题，并设计了蚁群算法进行求解.王鹏飞等[16]以社会福利最大化为目标研究了不同泊位提供者组合条件下出行者有偏好的泊位匹配问题.

现有共享停车匹配问题更多关注于停车选择和共享停车位分配，鲜有综合考虑出行者和停车位共享者双方收益，基于此，本文将出行者和停车位共享者作为两个独立的主体，利用熵权法确定多属性权重，并建立多目标双边匹配决策模型，对多属性条件下的多目标共享停车位匹配问题进行深入研究.

1 问题描述

目前，共享停车作为缓解停车压力的有效措施已被很多城市应用以城市解决停车难问题.因城市停车需求远大于停车供给，故小汽车出行者需要在出行前通过共享停车平台进行停车位预定，然后驾车到共享停车位停车，最终步行至目的地；此种出行方式称为“驾车+共享泊位停车+步行”.设出行者集合为R={r1,r2,…,ri,…,rm}，其中ri表示第i个出行者(小汽车驾驶者)，且i=1,2,…,m，设共享停车位集合P={p1,p2,…,pj,…,pn}，其中pj表示第j个共享停车位，且j=1,2,…,n.其中任一出行者ri(ri∈R)的出行起讫点为(oi,di)，则整个共享停车出行过程如图1所示.

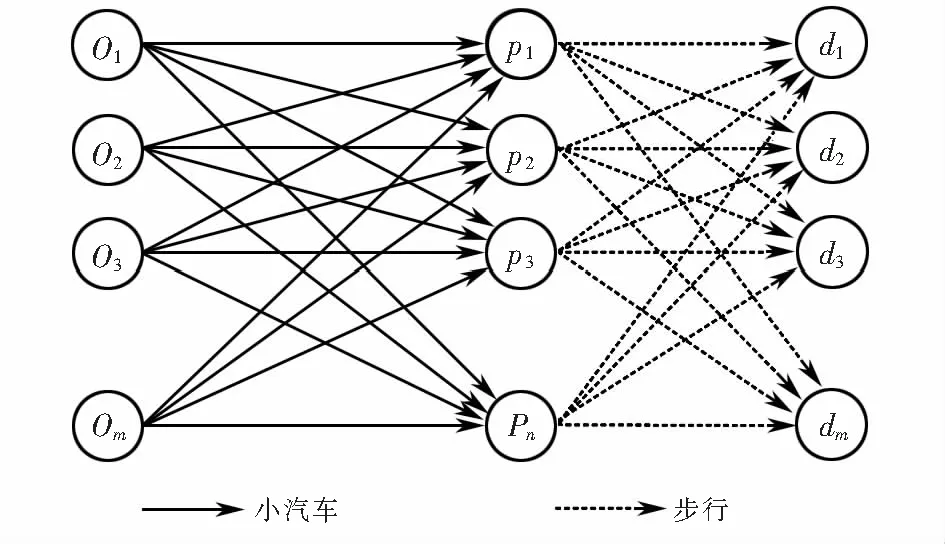
图1 共享停车出行过程Fig.1 Shared parking travel process

2 问题分析与建模

共享停车位匹配是一个涉及出行者、共享者以及共享平台的多方案、多属性、多目标复杂问题，不同的参与主体会根据不同的收益评价来判断并选择适合于自身的匹配对象，最终达到出行者和停车位共享者之间的匹配，完成出行任务.

2.1 参数定义

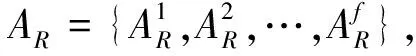
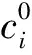
2.2 权重计算

共享车位匹配双方需求属性在实际应用中类型较多，如：收益型、成本型等.在匹配过程中，出行者和共享者对各自属性关注程度存在差异，称这种差异性关注程度为属性偏好权重.出行者和共享者通过对匹配属性的综合评价选择最佳的匹配者，共同完成共享车位匹配.因此偏好权重的确定至关重要，偏好权重必须能最大程度反映不同属性对车位匹配方案的影响程度.

Step1：为消除因属性量纲和数量级不同对计算结果的影响，进行无量纲规范化处理，计算公式如下.

1) 对于成本型属性：

(1)

2) 对于效益性属性：

(2)

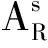
(3)

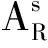
(4)

其中:k1=1/ln(m),k2=1/ln(n).

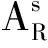
(5)

2.3 收益分析

1) 出行者收益分析

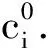
2) 共享者收益分析

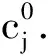
2.4 模型建立

在停车位共享匹配过程中，参与匹配的双方主体都是以极大化各自收益为目标，设xij为决策变量，其中xij∈{0,1}，如果出行者ri成功与共享停车位pj匹配，则xij=1，否则xij=0.本文假设实施共享停车后停车位能满足现状需求，即m≤n，根据双边匹配理论，建立多目标模型如下：

(6)

(7)

(8)

(9)

xij∈{0,1},i=1,2,…,m;j=1,2,…,n.

(10)

其中：公式(6)表示所有出行者出行节约成本最大；公式(7)表示所有共享停车泊位节约成本最大；公式(8)表示每位出行者在共享泊位匹配过程中都能找到1个满意的共享停泊位；公式(9)表示每个泊位共享者在共享泊位匹配过程中最多找到1个满意的出行者；公式(10)表示xij为0-1变量，即出行者ri成功与共享停车位pj匹配，则xij=1，否则xij=0.

2.5 模型化简与求解

上述模型中出行者和共享车位共享者都追求收益最大，将使用集结算子将目标函数ZR和ZP合并，化简为综合考虑双方收益的单目标模型，表示如下：

(11)

(12)

(13)

xij∈{0,1},i=1,2,…,m;j=1,2,…,n.

(14)

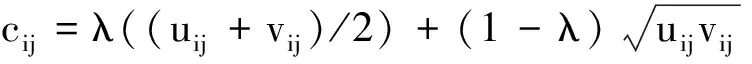
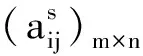
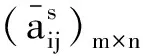
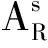
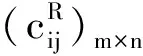
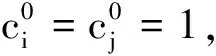
Step6：根据出行者和共享停车位数目，虚拟n-m个出行者，令其费用系数uij=0，vij=0；

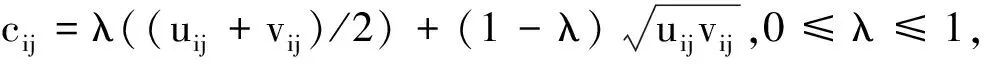
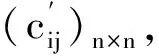
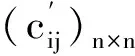
Step10：计算原模型目标函数值Z=nc0-Z′，给出最终匹配方案.

3 算例分析

已知来自不同区域的7位出行者将于预定时间前往某区域毗邻的7个目的地去上班，现因目的地停车位不足，通过共享停车平台查找到8个符合条件的邻近共享停车位，详细信息如表1～2所列.在出行者和共享车位匹配的过程中，出行者关注的属性有前往停车位的驾驶时间、停车后的步行距离、停车费用、停车安全性、停车便捷性和车位共享者的诚信度；而泊位共享者关注的属性有停车收益、共享停车位的利用率和出行者的诚信度.

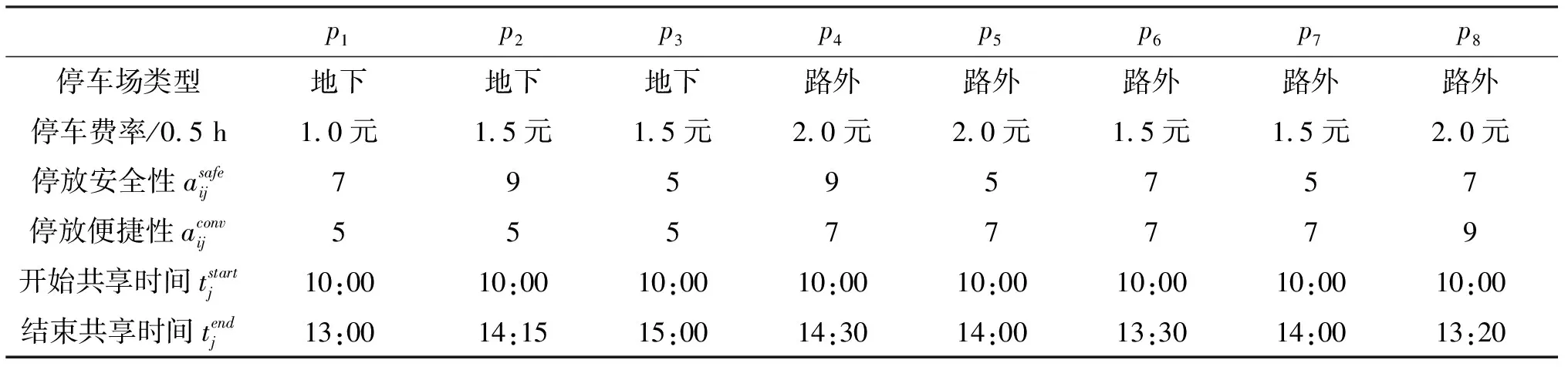
表1 共享停车位信息

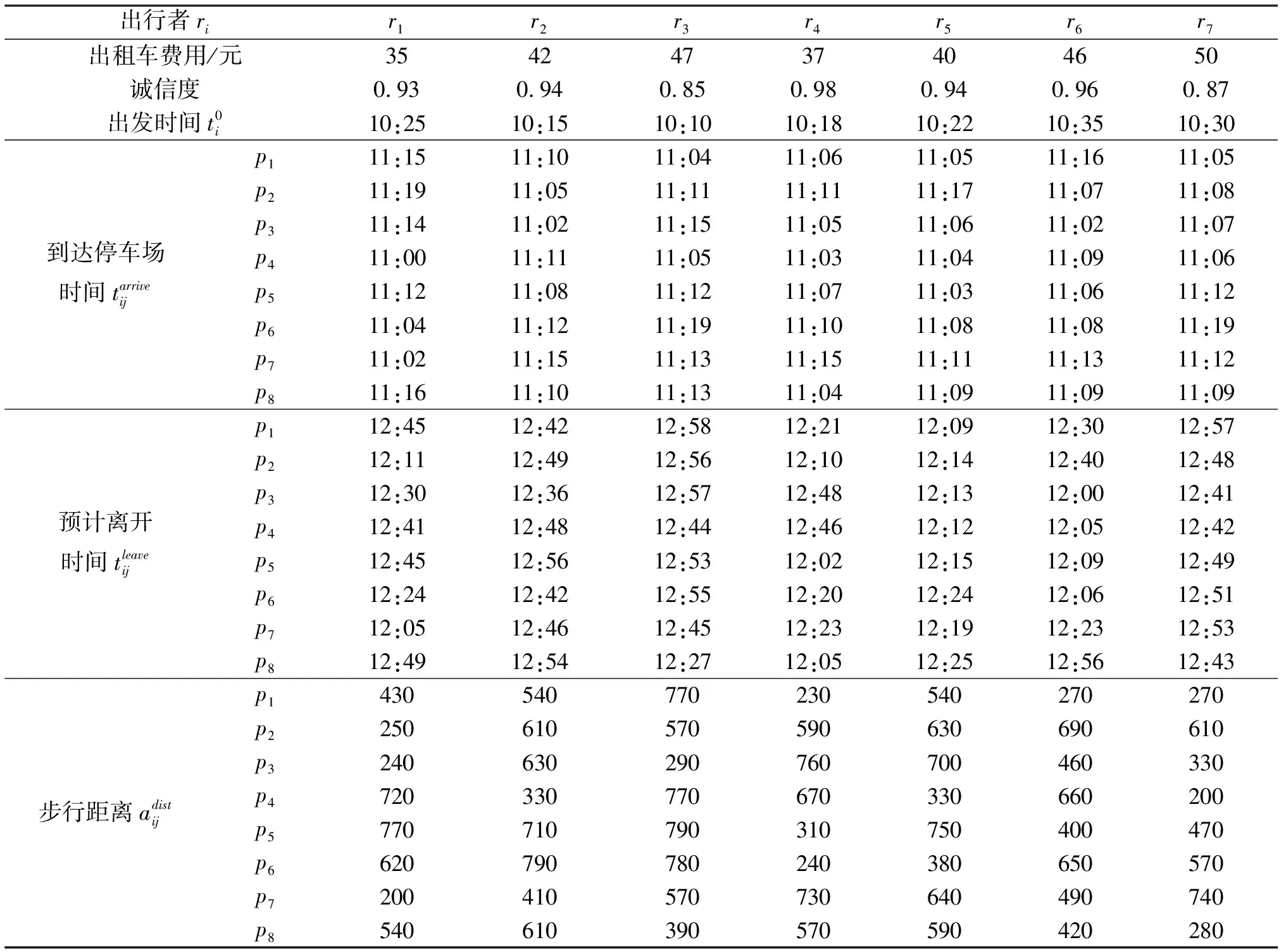
表2 出行者出行时间与步行距离信息

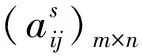
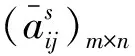
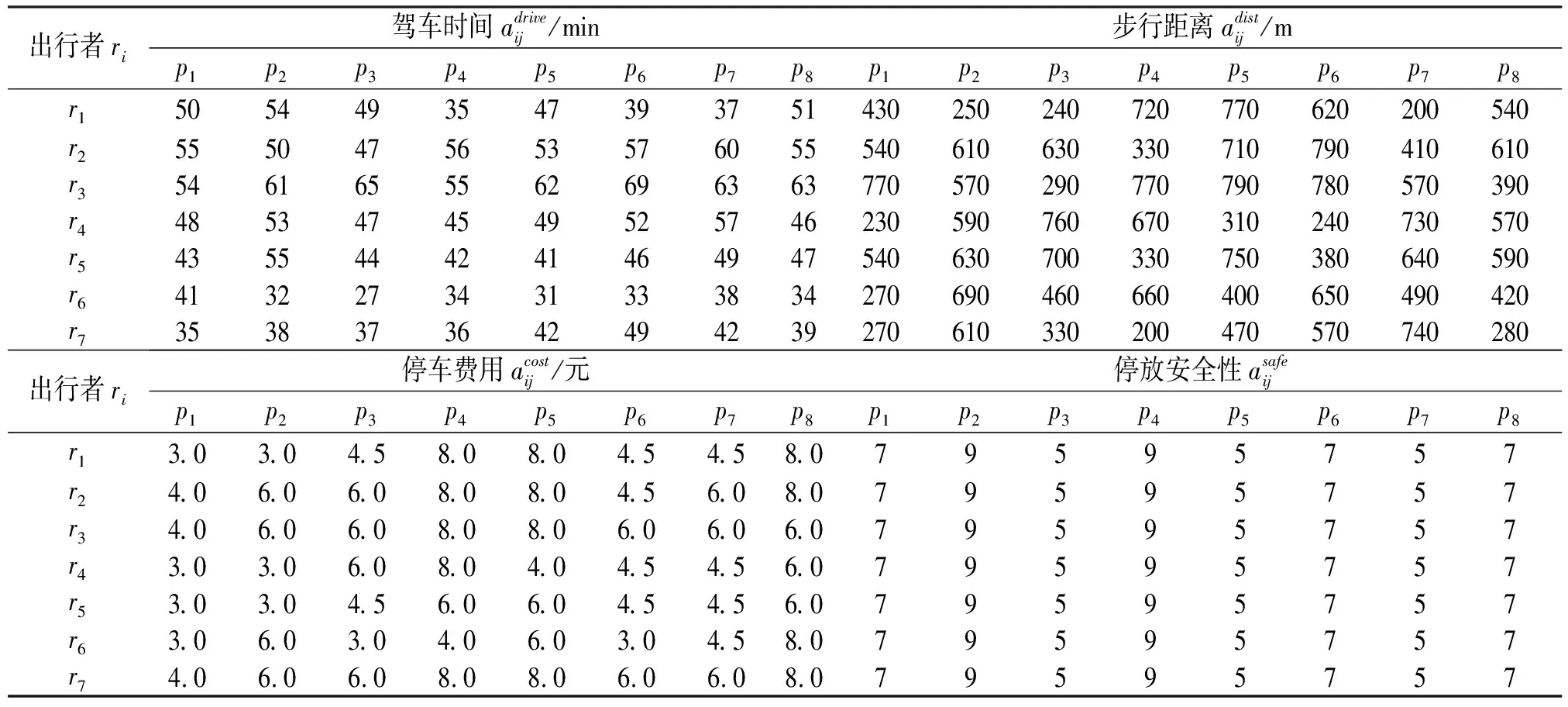
表3 出行者匹配决策属性数据表

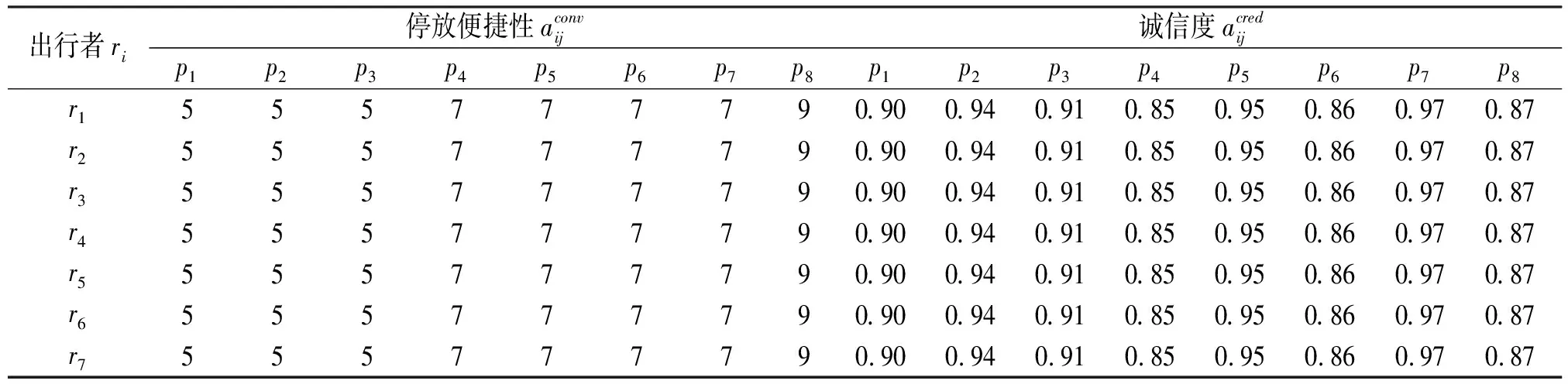
续表

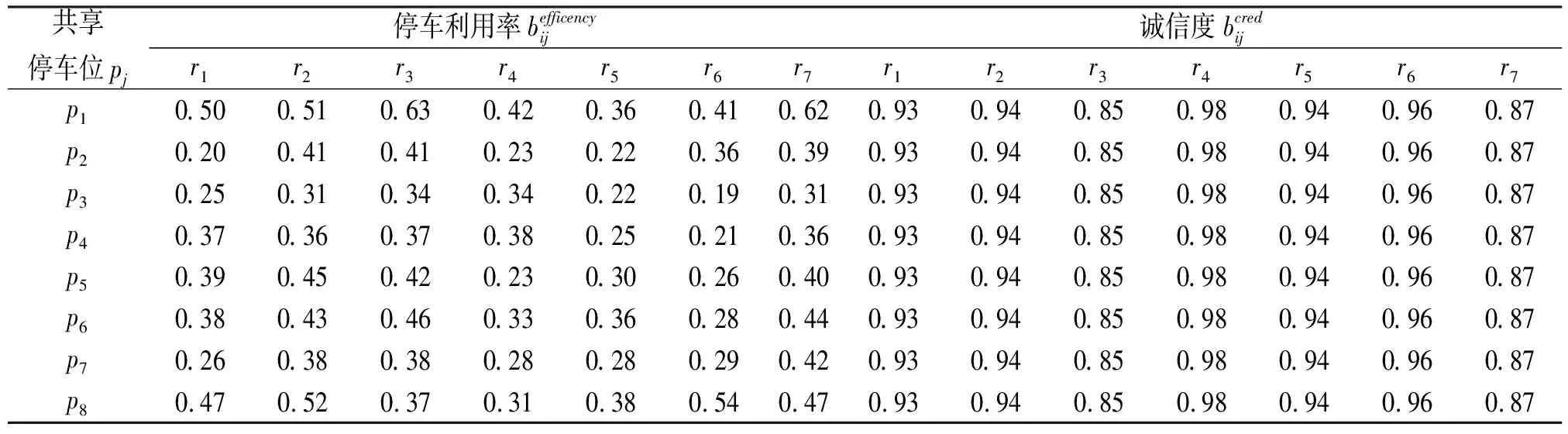
表4 共享停车位匹配决策属性数据表

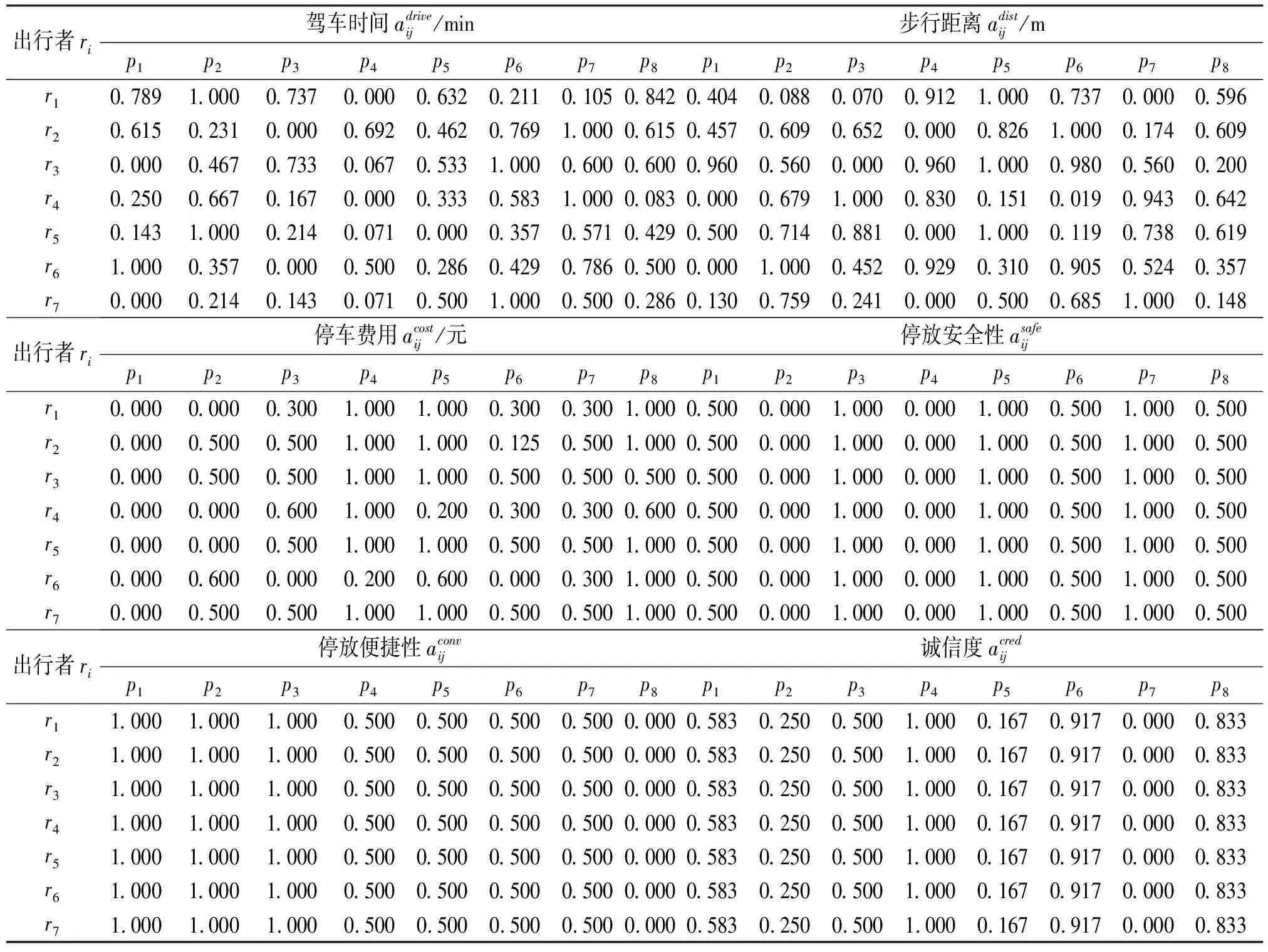
表5 出行者匹配决策属性规范化数据表

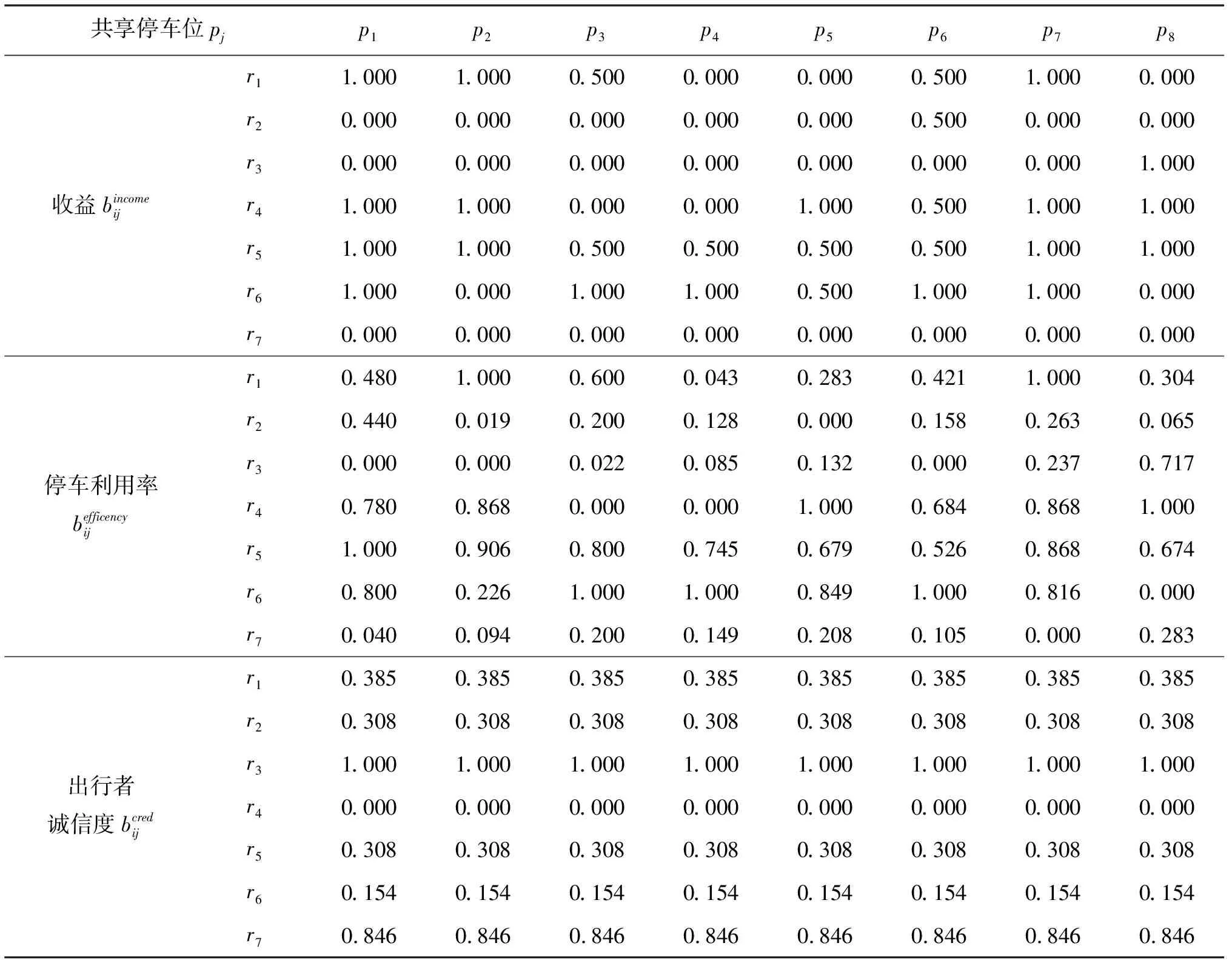
表6 共享停车位匹配决策属性规范化数据表

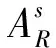
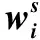
表7 出行者各属性偏好权重

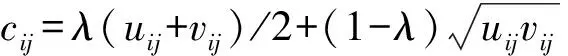
通过上述对比结果可知，当匹配时对出行者和泊位共享者收益的重视程度不同，因而得到的结果差异较大，在所有求解情形中除了(r5,p6)稳定外，其他匹配组合在不同程度上有所变化.现作如下对比分析：

1) 对比Case1和Case13的匹配结果可以发现，当分别考虑出行者的收益或者泊位共享者的收益时，所得到的匹配结果差别较大.

2) 因case3中cij=(uij+vij)/2，属于公平考虑出行者和停车位共享者的收益，将此情形下得到的匹配结果与Case1和Case13进行对比，结果如表12所列.

从表12对于公平考虑出行者和停车位共享者收益与只考虑出行者收益时的匹配结果对比，发现稳定的匹配结果数目为2个，占总数的25%；但从公平考虑出行者和停车位共享者收益与只考虑停车位共享者收益时的匹配结果对比，发现稳定的匹配结果数目为4个，占总数的50%.说明考虑双边主体收益公平性所得到的结果偏向于仅考虑出行者收益的结果.

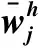
表8 共享者各属性偏好权重

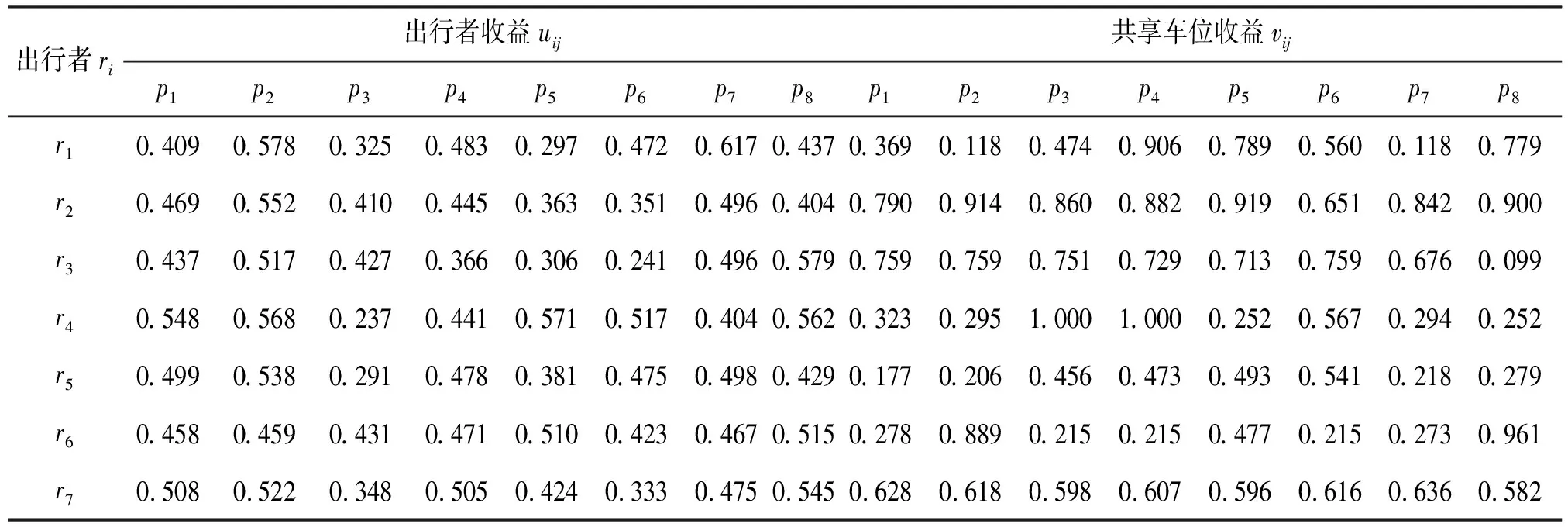
表10 出行者与共享车位收益

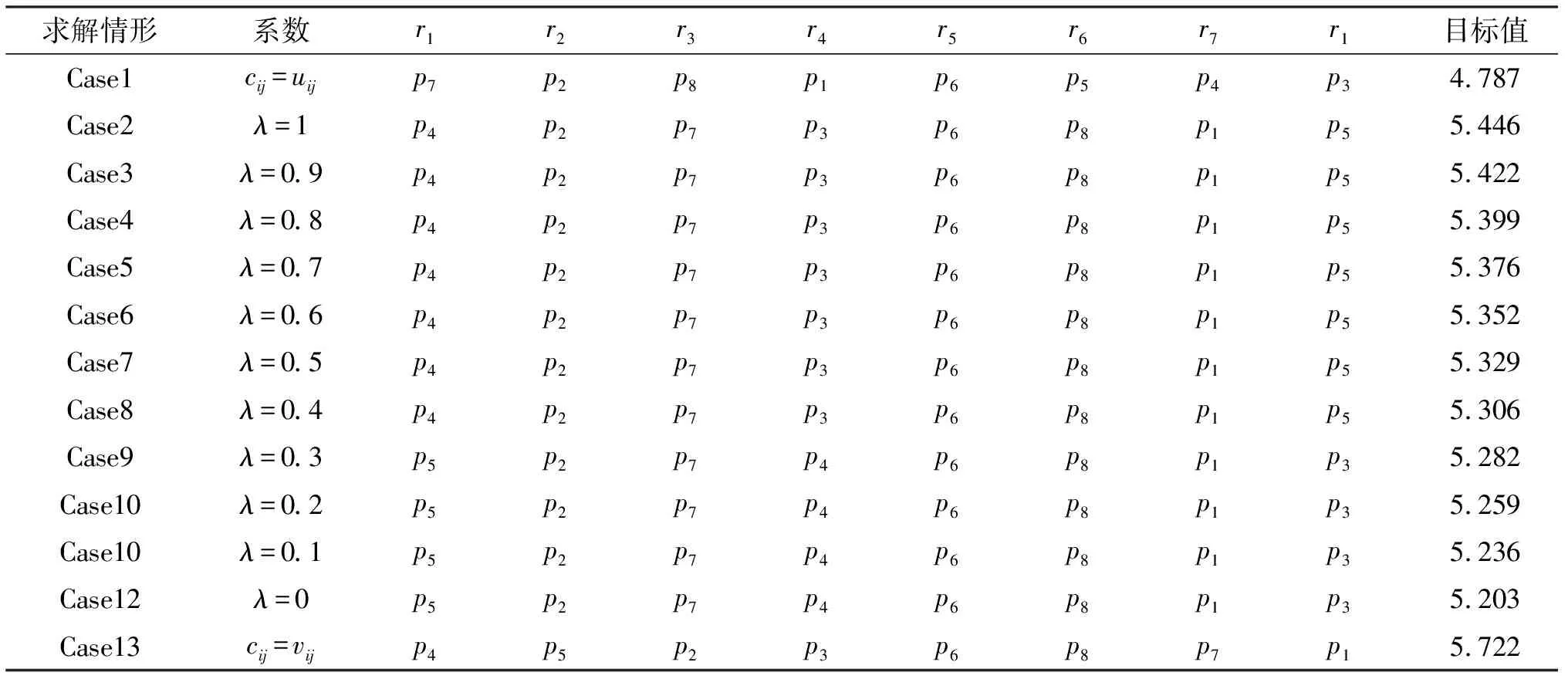
表11 不同情形下匹配结果分析表

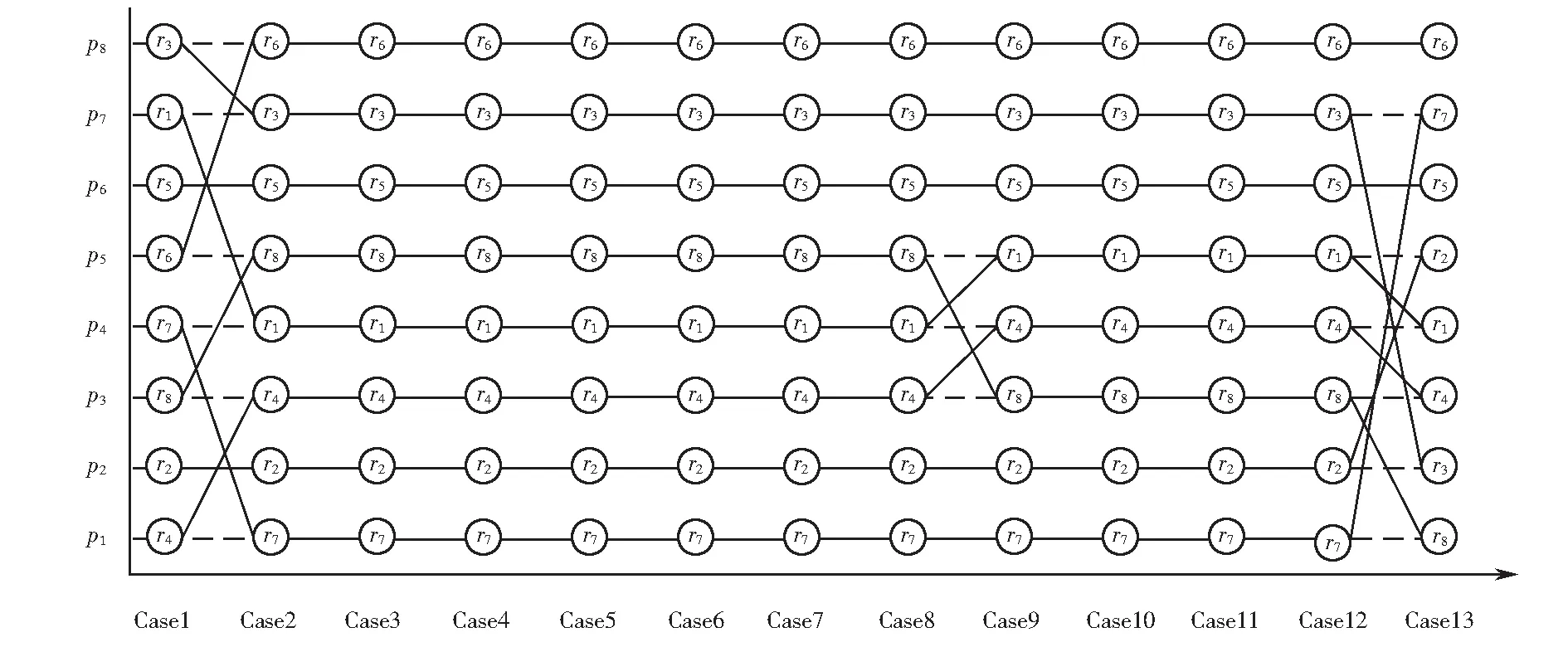
图2 不同情形下出行者与停车位匹配结果Fig.2 Matching results of travelers and shared parking spaces in different situations

表12 考虑双方公平收益与只考虑一方收益结果对比

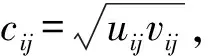
通过表13可知，对比考虑出行者和停车位共享者收益一致性与只考虑出行者收益或者只考虑停车位共享者收益时的匹配结果，发现稳定的匹配结果数目都为2个，占总数的25%，说明此时的结果没有出现偏向于任何一方的现象.

4) 通过综合对比Case2到Case12中，随着λ值变小，整个目标函数值呈现递增趋势，同时匹配结果也会发生小范围变化，不同λ取值时的匹配结果综合对比如表14所列.

表13 双方综合收益与一方收益结果对比

表14 不同λ取值时匹配结果对比

由表14结果对比可知，随着λ值的变化，出行者与共享停车位的匹配结果会产生一定程度的变化，但有5组匹配结果相对稳定，稳定匹配对个数占总数的62.5%，说明在不同λ取值范围内得到的匹配结果能同时满足大多数出行者和停车位共享者的收益.

5) 通过目标值对比发现：Case2至Case12中综合考虑出行者和共享者收益的公平性和一致性的时得到的目标均值大于仅考虑出行者Case1和仅考虑共享者Case13收益的平均值，收益平均增幅1.40%.当λ≥0.2时目标值均大于只考虑出行者和出行者收益的平均值，说明0.2≤λ≤1时所有的匹配方案较优.

4 结论

考虑多属性的出行者和共享者双独立主体匹配模型能很好地描述共享停车位匹配相关问题，匹配结果可同时满足出行者和车位共享者的匹配需求.后续研究将聚焦多属性标准化后的权重确定，分析出行者感知效用及不同心理需求的共享停车位匹配.