基于改进SSD的低截获概率雷达辐射源识别算法

赵 帅，刘松涛，汪慧阳

(海军大连舰艇学院信息系统系，辽宁 大连 116018)

0 引言

雷达辐射源识别(emitter identification，EID)是认知电子战系统的重要功能模块之一[1]，其在提取分选信号核心特征的基础上识别信号类型，为判断威胁等级、构建战场态势、推理战术意图提供重要参考。在现代战场电磁环境的复杂度及交战双方电子攻防激烈程度不断提高的背景下，低截获概率(low probability of intercept，LPI)雷达得到广泛应用，其通过脉冲压缩技术实现强抗干扰能力及低截获特性,大大提高了雷达对抗一方的信号捕获及识别难度。因此，自动有效识别LPI雷达信号对提高电子对抗能力具有重要的研究意义。

当前，已有学者对LPI雷达辐射源识别问题进行了初步研究。文献[2—3]分别使用多层感知机(multi-layer perceptron，MLP)和Elman 神经网络(elman neural network，ENN)学习大量人工设计选择的信号特征，实现了较好的LPI雷达信号识别效果，但算法受载频估计准确性的影响很大且依赖人工设计提取特征。文献[4]直接使用多种(wigner-ville distribution，WVD)图像分别作为多CNN分支网络输入，避免了人工提取特征的过程，并通过特征融合强化识别效果，但网络结构较为复杂。文献[5]则在LPI雷达信号(choi-william distribution，CWD)的基础上，进行了单CNN网络识别信号类型的研究。近年来，基于目标检测的LPI雷达信号分类算法被提出并展现出独特的优势，其不仅可以确定信号类型，还可以定位图像中的目标信号区域，很好地解决了非目标脉冲信号的干扰问题。文献[6]使用原始SSD模型[7]进行了相关方面的初步研究，但并未考虑模型实时性这一关键属性。

针对该领域基于目标检测类方法实时性不高的问题，本文提出一种基于改进SSD的LPI雷达辐射源识别算法，进行7种常见LPI雷达信号的分类识别研究，包括线性调频、Barker码、Frank码以及P1—P4码。

1 SSD模型

SSD模型作为一种基于回归的单级(one-stage)目标检测网络，目标分类与预测框回归同时进行，兼顾了识别精度和检测效率。通过对VGG-16网络的部分保留、修改及删补构成具有11级卷积层的SSD基础网络结构，并由不同的中间卷积层输出6种尺度的特征层(feature map)，用来检测不同大小的目标。SSD基础网络结构如图1所示。

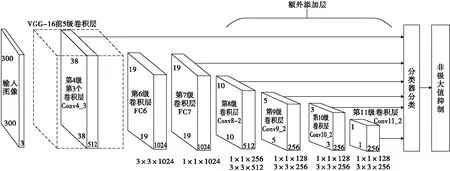
图1 SSD网络结构图Fig.1 SSD network structure

具体流程：将图片输入SSD网络后，自动调整尺寸为300×300，各卷积层相继提取不同深度的特征，生成6种尺度的特征图(38×38，19×19，10×10，5×5，3×3，1×1)，将特征图分割为对应尺度的单元格，并在每一个单元格上生成既定数量的先验框。先验框中存在有大量的负样本，即与真实框交并比(intersection-over-union，IoU)小于0.5的框样本，其数量远超正样本且其有效信息少，往往拖慢网络训练、降低检测效果。SSD模型采用难例挖掘解决正负样本不平衡现象，通过对先验框的类别置信度排序，以3∶1的比例选取正负样本。设网络每个特征层对应的先验框总数为Ni，随后对每个特征层进行一次Ni×4的卷积用以确定该特征层每一个单元格上每一个先验框的位置偏移，包括真实框与先验框中心点在x轴、y轴上的偏移情况以及两框的宽、高偏差情况，再进行一次Ni×Nc的卷积，其中Nc为预测类别数，用以确定每个先验框对应的类别置信度。

训练阶段，通过迭代确定网络权重，最小化损失函数Loss最大程度地将预测框回归到真实框，Loss函数由两部分加权构成，分别为样本位置(loc)损失以及样本的置信度(conf)损失，如式(1)所示：

(1)

式(1)中，N为与真实框相匹配的先验框个数，当N为0时，设置损失值为0；c为目标置信度，l和g分别为预测框及真实框参数，权重α取值为1。Lloc(x,l,g)为目标位置偏移损失，Lconf(x,c)为置信度损失。样本位置损失表示为：

(2)

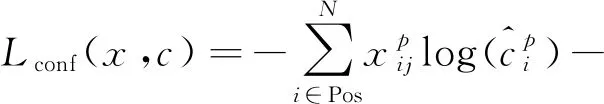
(3)

式(3)中，Pos,Neg分别表示正负样本。

预测阶段，SSD网络预测每个先验框的类别置信度和位置偏移量，采用非极大值抑制算法(non-maximum suppression，NMS)对先验框进行筛选得到最终的预测框。

作为一种基于回归的单级检测网络，SSD算法有着远超R-CNN[8]、Faster R-CNN[9]等基于候选区域的两级检测算法的检测速度，更易满足实时性要求，同时得益于更多尺度特征图的融合，与同样是单级检测网络的YOLO[10]算法相比，SSD算法的检测精度也更高。需要说明的是，尽管SSD算法兼顾速度与精度，但两者都不是最优，仍有可提高的空间。

2 基于改进SSD模型的辐射源识别算法

为进一步提高SSD模型的识别精度和实时性，本文采用准确度更高、速度更快及更为轻量化的ResNet-50网络代替VGG-16网络搭建SSD模型，并对ResNet-50网络进行相应改进，以期获得更好的LPI雷达信号识别效果。

2.1 基于ResNet-50的SSD网络结构

VGG-16网络是传统CNN结构的简单堆叠，参数数量大，且随着网络的加深会出现梯度消失和梯度爆炸的问题以及网络训练效果不升反降，即网络退化问题。2015年，ResNet[11]问世，通过引入批归一化(batch normalization，BN)层和残差(Residual)子块解决了这两个问题。BN层对中间层的特征图进行归一化处理，以加速网络收敛并提高准确度，避免梯度消失和梯度爆炸问题的出现。残差子块通过在网络层与层之间增加跳跃连接，将前层最优权值直接传递到后层，拟合残差映射达到消除网络退化的效果，该结构还一定程度上减少了模型参数量，增加了检测网络的效率及精度。VGG-16与ResNet-50网络参数量与复杂度对比如表1所示[11-14]。

表1 VGG-16与ResNet-50网络复杂度对比

网络参数量是衡量网络大小的重要参数，通常按照下式计算：

(4)

浮点运算次数(floating point operations, FLOPs)是衡量网络复杂度的标准参数，其计算可依据下式[14]：

(5)

式(4)、式(5)中，H、W及Cin分别为输入特征图的高、宽及通道数；K为卷积核宽度，Cout为输出通道数；I、O分别为全连接层的输入、输出维度。

从表1中可直观看出，ResNet-50的参数量、浮点运算次数均远低于VGG-16，证明了其更为轻量化，也具备了具有更快速度的条件。

使用ResNet-50网络搭建SSD模型需做出如下改进[15-16]：首先保留ResNet-50的前4级卷积模块，移除随后的第5级卷积模块、全连接层及Softmax层；为保证第1级feature map的尺寸依然为38×38，将第4级卷积模块的第1个残差子块的步长(stride)全部修改为1，避免其降维；额外增加5级层结构，分别输出尺度为19×19，10×10，5×5，3×3及1×1的feature map，并在该5级层结构中加入BN层结构以加强网络表征能力。基于ResNet-50的SSD模型结构如图2所示。

由于基于ResNet-50的SSD模型特征图、先验框的生成与原始模型并无差别，在该两种模型复杂度的比较方面，本部分仅对其特征提取网络进行分析。按照式(4)、式(5)，粗略计算得到的两种模型特征提取网络部分的参数量与浮点运算次数如表2所示。

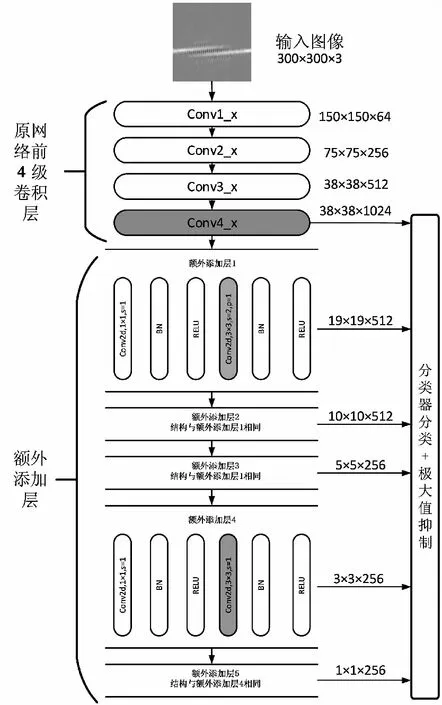
图2 基于ResNet-50的SSD模型结构图Fig.2 SSD model based on ResNet-50

表2 理论上VGG16-SSD与ResNet50-SSD模型复杂度对比

2.2 LPI雷达辐射源识别算法

为完整地模拟雷达辐射源识别过程，本文的识别算法框架如图3所示。天线侦收到射频信号，经过一系列操作输出可处理的中频信号。通过时频分析算法处理中频信号得到时频图像，然后利用人工标注等预处理训练SSD模型，或者将其输入训练好的模型进行检测识别。

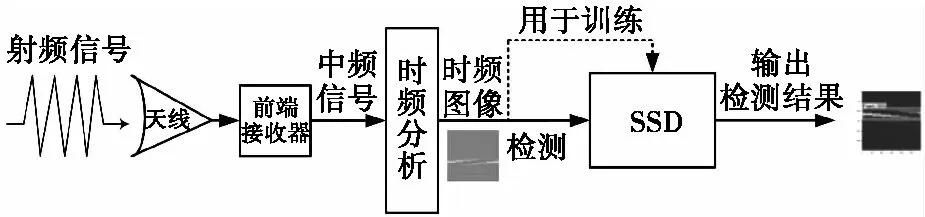
图3 辐射源识别算法框图Fig.3 Block diagram of emitter recognition algorithm

在众多的时频分析算法中，WVD算法具有最高的时频分辨率，但在处理多分量信号时易产生交叉项干扰。SPWVD(smoothed pseudo wigner-ville distribution)作为WVD的改进版本在保持高时频分辨率的基础上，很好地抑制了交叉项干扰。本文即采用SPWVD作为时频分析方法，信号s(t)的SPWVD定义如下：

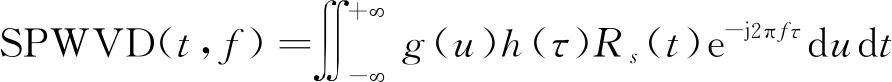
(6)

式(6)中，t与f分别代表时间和频率，g(u)和h(τ)为两个汉明窗函数，满足g(0)=h(0)=1。

3 仿真实验

3.1 建立LPI雷达信号数据集

LPI雷达信号多通过频率编码和相位编码等脉冲压缩技术来实现低截获特性，频率编码以线性调频(LFM)为代表，相位编码分为二相编码及多项编码，前者以巴克码(Barker)为主，后者则有Frank码、P1、P2、P3及P4多种编码选择。本文建立的数据集主要以该7种LPI雷达信号为主，具体信号参数选择如表3和表4所示。

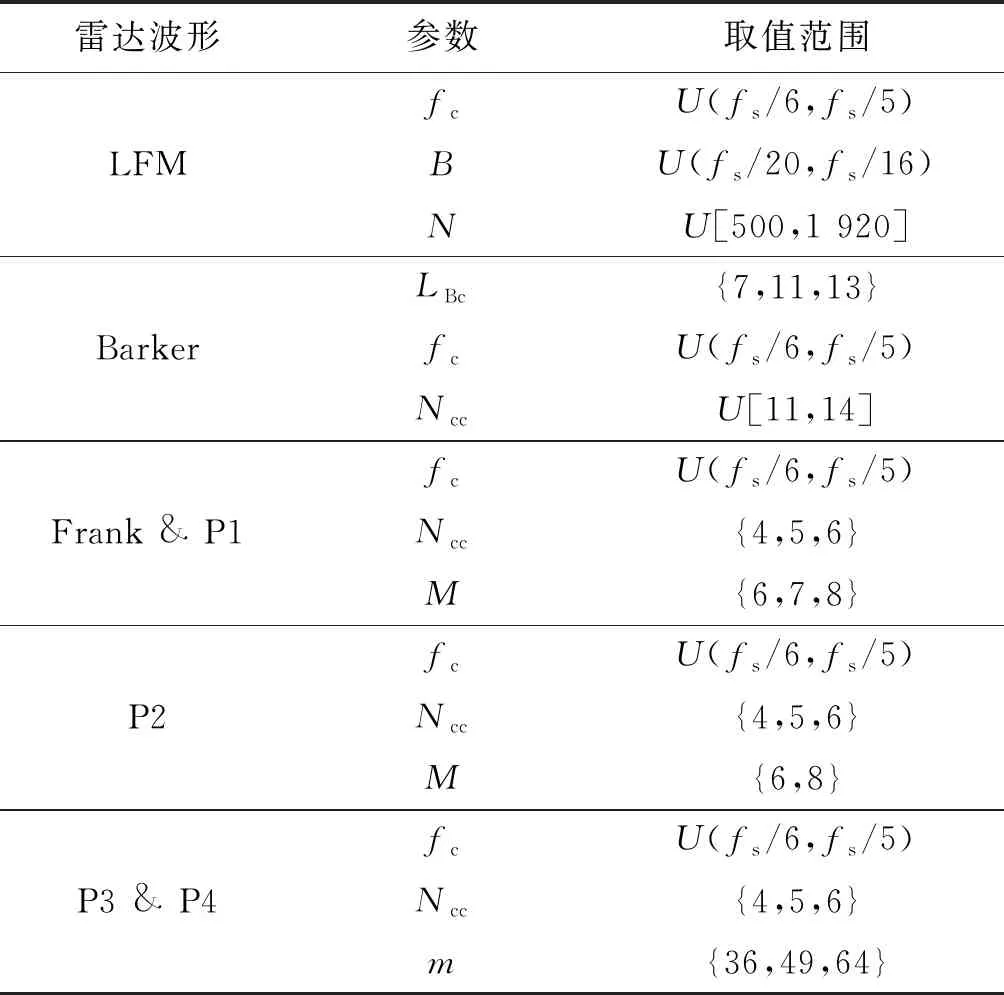
表3 7种LPI雷达信号仿真参数

表4 数据集仿真条件设置

大多数此方向的研究[2-6]均仅考虑AWGN的影响，与真实信道环境差距较大。本文对生成的原始训练信号随机施加SNR范围为[-6,30] dB的AWGN以及范围为[fs/6,fs/5]的载频偏移，并在此基础上构建莱斯衰落信道模拟信号传输过程，具体信道参数如表5所示。

依据以上参数完成信号仿真后，通过SPWVD时频分析获取信号的时频图像作为SSD模型的输入。同一信号由WVD与SPWVD获取的时频图像对比如图4所示。

表5 莱斯衰落信道参数

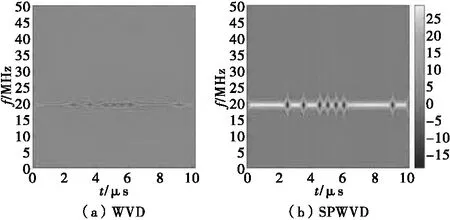
图4 同一信号的WVD与SPWVD时频图像Fig.4 WVD and SPWVD time-frequency images of the same signal

对比图4(a)、(b)两图，和前面理论分析一致，SPWVD的效果远远好于WVD的效果。7种LPI雷达信号的SPWVD时频图像展示如图5。

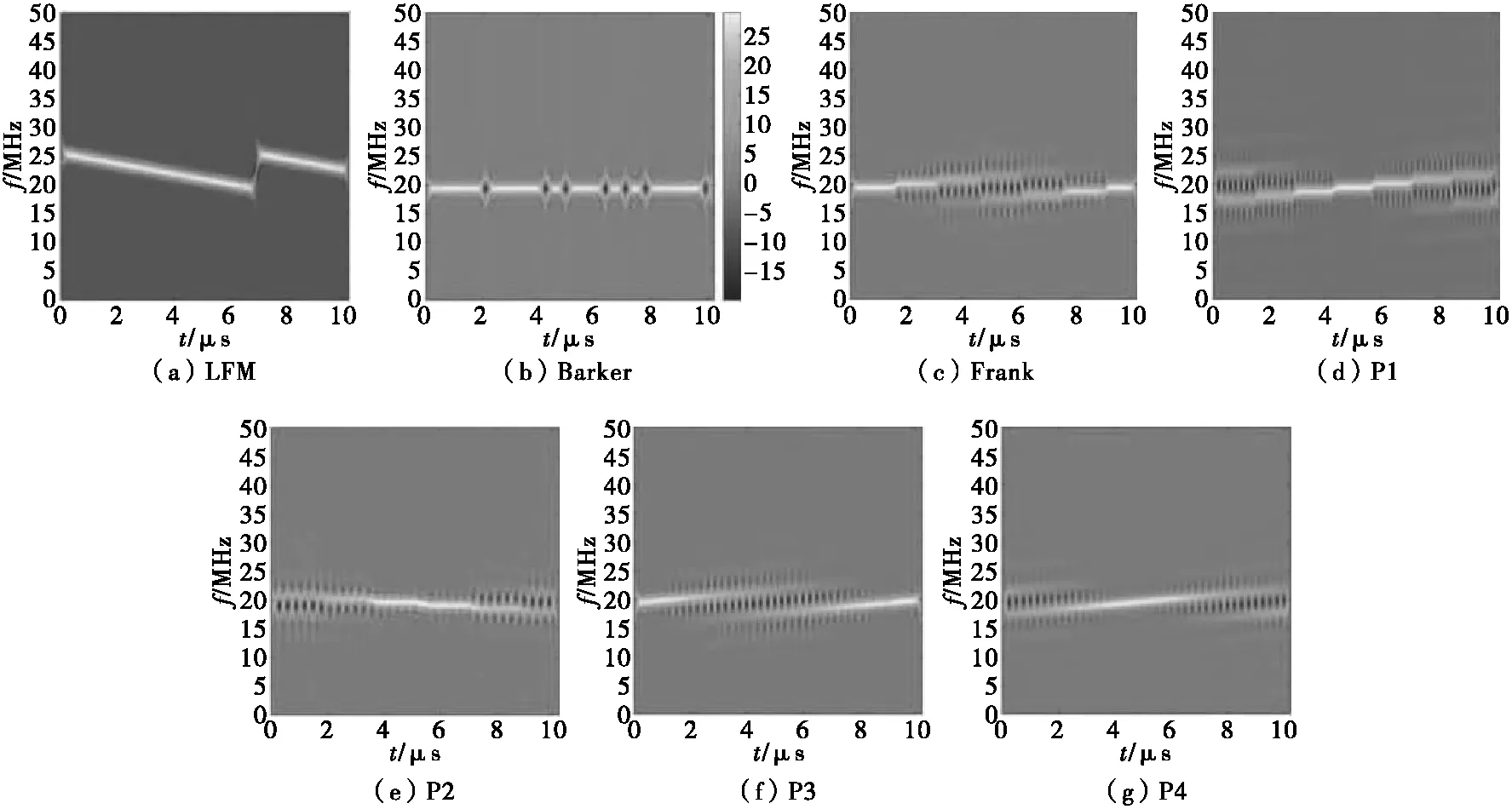
图5 7种LPI雷达信号的SPWVD时频图像Fig.5 SPWVD time-frequency images of seven LPI radar signals

分析7种LPI雷达信号时频图像特征如下：LFM及Barker信号具有较为明显的区分特征，其余5类多相编码信号时频图像较为相似，但也有着可区分的个体特征表现：Frank，P1及P2时频图像具有明显的阶梯状特征，而P3，P4信号则为边缘光滑的直线段；Frank及P3信号能量中心分布于图像左右两侧，而P1及P4能量中心聚集于图像中心；P2信号与P1图像特征极为相似，但两者时频图像中特征线段走势相反，P2为下行，P1为上行。总之，7种时频图像具有SSD模型可区分的不同特征，从而使用SSD模型进行LPI信号识别算法具有可行性。

3.2 改进SSD模型的训练和检测测试

使用LabelImg工具将用于训练的7 000张图片进行人工标注制作成PASCAL数据集，并按8∶2的比例将其分为训练集和验证集。由于各类LPI雷达信号时频图像的相似性，不对数据集进行翻转、平移及模糊等数据增广处理。实验平台参数如下：Intel(R) Core(TM) i7-8750H CPU@2.20 GHz 处理器，16 GB内存，4 GB NVIDIA GeForce GTX 1060 GPU，Pytorch深度学习框架。将数据集放入改进后的模型进行训练，设置Epoch=15，初始学习率为0.000 5，并随着迭代次数增加逐步减小学习率。训练过程Loss函数及学习率变化如图6所示。

图6 训练时Loss函数及学习率变化Fig.6 The change of Loss function and learning rate during training

进行目标检测时，设置目标框得分阈值为0.5，当得分大于等于0.5时显示预测目标框。依据表4建立测试集对模型进行测试，部分检测结果示例见图7，图中依次展示了7种LPI雷达信号的检测结果示例，并选取Barker、P3两种信号进行了不同SNR下的检测效果展示。

如图7所示，模型在检测时将信号目标框起并显示目标类型及检测得分，在噪声淹没严重、主观难以分辨的情况下，模型也能准确地实现对目标的检测。

图7 目标检测结果示例Fig.7 Example of target detection results

3.3 改进SSD模型的性能评估

首先对模型的复杂度进行实际评估，该部分由Pytorch框架的thop模块和ptflops第三方库分别进行实现，两种实现方式结果一致，如表6所示。

对比发现，改进后SSD模型参数、浮点运算次数更少，复杂度更低。特征提取网络部分的参数值与前面的理论分析基本一致。两种模型的参数量和浮点运算次数均集中在骨干网络，其余部分所占比例很小且两种模型相差不大，由此证明骨干网络是决定SSD模型复杂度的关键，使用ResNet-50网络替换VGG-16网络是可行且正确的选择。

表6 SSD模型与改进SSD模型复杂度实际对比

其次对模型的速度进行评估，对比项包括训练时迭代一次所需时间(time per epoch，TPE)，单位为秒(s)，取训练过程中15次迭代的平均值；在CPU上每秒检测图片张数(CPU-FPS)以及在GPU上每秒检测张数(GPU-FPS)，取7类11种SNR共77个测试子集的检测平均值。通过改进模型与SSD模型的对比，客观评价改进SSD模型的性能。模型速度对比如表7所示。

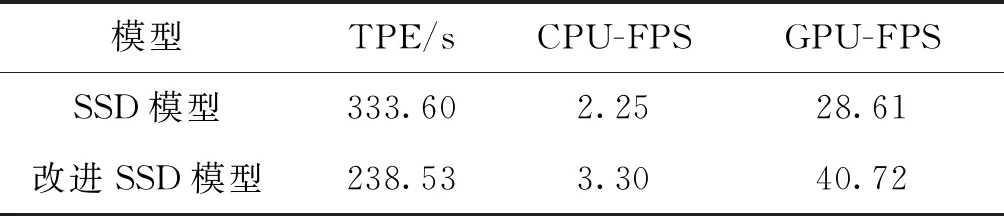
表7 模型速度性能评估

表7结果说明，改进SSD模型具有比原始SSD模型更好的实时性。改进SSD模型训练时迭代一次所需时间缩短了28.50%，在GPU上的检测速度提高了29.74%。

然后通过对比模型对测试集的检测准确率来评估模型的精度性能。所建立的测试集共包括15 400张图片，每类LPI雷达信号在每分贝(dB)SNR下有200张测试图片，SNR范围为[-10,10] dB，间隔为2 dB。现选取改进SSD模型在SNR为{10,6,2,-2,-6,-10} dB下的检测结果展示为表8。

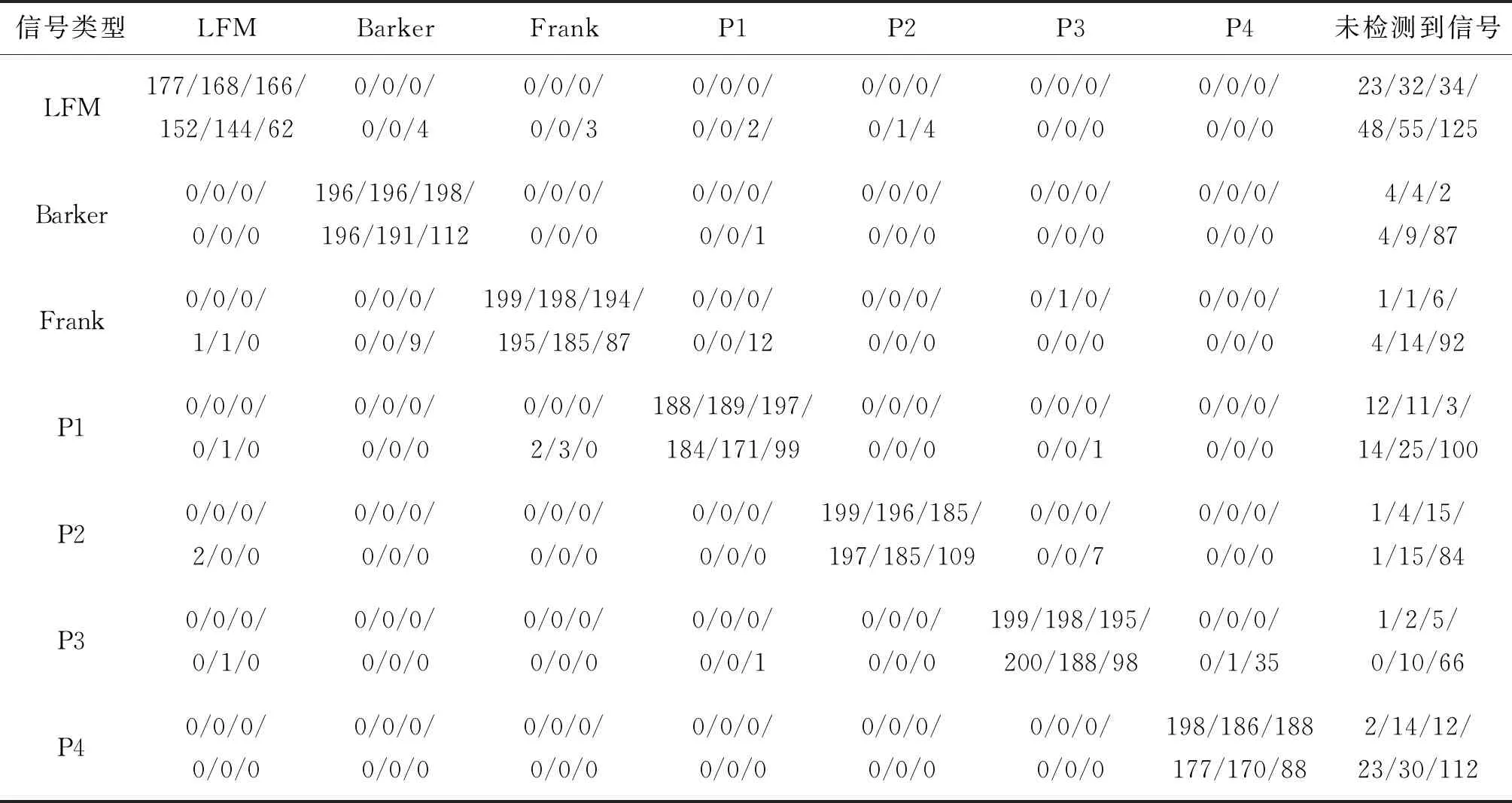
表8 改进SSD模型在SNR为{10,6,2,-2,-6,-10} dB下的检测混淆矩阵

表8中行表示LPI雷达信号的实际类型，列表示改进后SSD模型的预测类型。观察表中数据可知，在SNR=-10 dB时，模型分类表现大幅下降，出现了更多的“未检测到信号”类型的结果。与前面对7种信号的时频图像分析一致，在低SNR情况下，错检现象多发生在Frank与P1信号之间，以及P3与P4信号之间。

使用相同的训练集和测试集对原始SSD模型进行测试，得到的结果与改进SSD模型对比如图8所示。

分析图8(a)可知，改进后的SSD模型与原始模型在高SNR情况下均实现了较好的检测性能，在不低于-4 dB的情况下，可实现高于92.9%的检测准确率。但随着SNR的降低，原始模型准确率下降的更快，改进后的模型在低SNR情况下有着更好的稳定性。

分析各类LPI雷达信号的检测准确率变化，改进后模型对7类信号的检测准确率变化趋势基本相同，改进后模型对LFM，P3及P4三种信号在低SNR下的检测效果要远高于原始模型，由于该3种信号的时频图像均为光滑的直线段，在低SNR下信号被噪声淹没，区分度大大降低，原始模型的特征提取能力相对改进模型较弱，导致其检测效果变差。但需指出，改进后模型对P1及P4两种时频图像相近信号在高SNR下检测时效果略低于平均水平，推断原因为ResNet-50网络提取到了时频图像更为深层的特征而这些特征对P1及P4信号的区分度不高。

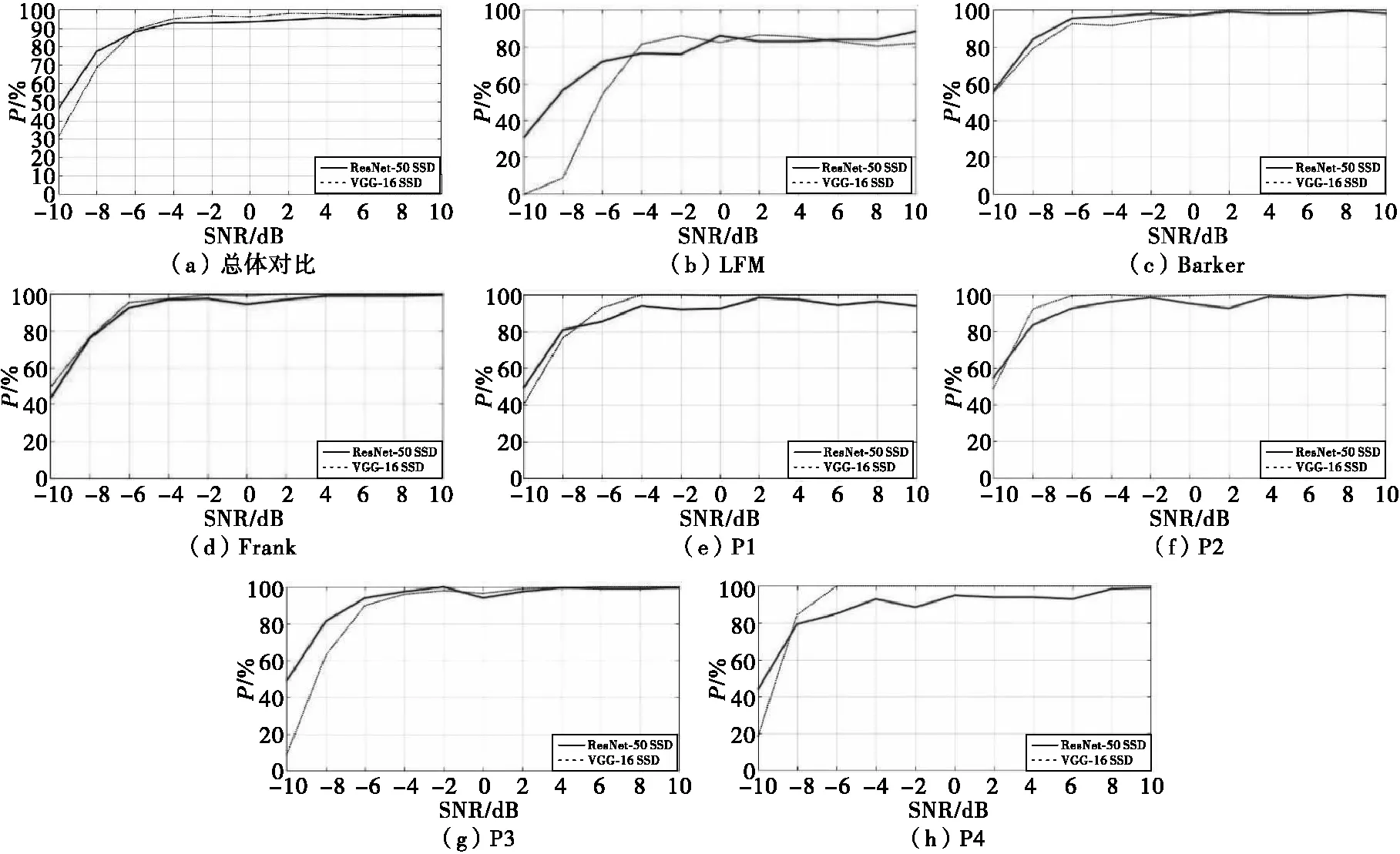
图8 改进模型与原模型的检测准确率对比Fig.8 Comparison of detection accuracy between improved model and original model

综上所述，改进后SSD模型在保持与原始SSD模型相近精度的基础上较大地提高了实时性，增强了工程实用性。

4 结论

在现代战场LPI雷达被广泛应用，将其快速准确识别具有重要意义。本文提出一种基于改进SSD的LPI雷达辐射源识别算法，并将其应用于7种常见LPI雷达信号的识别中。该算法采用精度更高、速度更快的ResNet-50代替原VGG-16网络，并对网络进行了改进设计。生成仿真数据时，为更贴近真实情况，构建了莱斯衰落信道用以模拟信号传播环境。仿真实验结果表明，在SNR=-4 dB时算法的识别准确率可达到92.9%，与原始SSD模型相比，训练及检测速度分别提高了28.50%和29.74%。后续工作将思考如何进一步提高模型在高SNR下的识别准确率及模型的抗噪能力。