磨粒有序排布曲面砂轮设计及磨削性能实验研究*

李瑞昊， 石广慧， 黄 辉

(华侨大学 机电及自动化学院， 福建 厦门 361021)

金刚石砂轮因其所具有的优异性能，在许多非金属材料的磨削加工中得到了越来越广泛的应用[1]。传统的金刚石砂轮中磨粒基本处于随机分布状态。由于磨粒的随机性，砂轮表面的磨粒易出现局部聚集及局部稀疏[2]。磨削时聚集部分因为容屑空间小，砂轮易堵塞，导致磨削温度过高，工件表面易产生磨削烧伤裂纹和热变形等现象，磨粒的磨损也更为严重，从而降低磨削效率；另一方面，磨粒稀疏的部分，单颗磨粒所承受的载荷相对过大，冲击力也相应增大，使得磨粒的磨损加剧，或出现磨粒非正常脱落，砂轮寿命显著降低[3]。

研究发现：当对砂轮表面金刚石磨粒的位置进行合理规划排布时，砂轮表面的每一颗磨粒可以承受相同的载荷，磨粒磨损均匀，可以有效地提高砂轮的使用效率和使用寿命，因此提出磨粒排布砂轮的概念[4]。目前，已有从排布样式、排布方法、排布效果等多个方面的大量研究，其结果进一步证实了有序排布砂轮的优异性能[5-8]。

曲面砂轮是实现曲面工件加工的主要工具之一。其基本思路是通过对砂轮形状的设计及控制，达到高效加工相应曲面工件的结果[9]。与普通的平面砂轮相比，曲面砂轮的直径会产生变化，这导致曲面砂轮表面不同位置处的磨粒线速度各不相同，磨粒的磨损也不尽相同。但目前尚无关于曲面砂轮表面磨粒排布的相关研究。

本研究提出一种应用于曲面砂轮表面磨粒有序排布的理论设计方法，制备出了磨粒有序排布的曲面砂轮，并从磨削力、工具磨损、工件形状误差等方面进行有序及无序曲面砂轮的对比磨削实验。

1 实验条件

砂轮的磨削磨损实验在BLOHM PLANOMAT HP 408 高速精密平面磨床上进行。磨削加工的工件材料为枫叶红石材，其性能参数见表1。工件尺寸为200 mm×48 mm×12 mm。实验中工艺参数保持恒定，砂轮速度为2 200 r/min，工件进给深度为18 m/min，磨削深度为10 μm。

表1 枫叶红花岗岩参数表Tab. 1 Parameter table of maple leaf red granite

实验所用的钎焊金刚石砂轮在沈阳威泰科技发展有限公司生产的VSF200型真空钎焊炉中制备。金刚石粒度代号为30/35、基本粒径为500～600 μm。选用Cu-Sn-Ti钎料，钎焊温度为900 ℃。

磨削实验过程中，利用Kister 9257B跟踪磨削力的变化，采样频率为10 kHz，并配备5080电荷放大器和5697A数据采集系统，采集系统连接电脑。测力时的工件尺寸为48 mm×12 mm×20 mm。磨削采用往复磨削的方式，即顺磨和逆磨交替进行。磨削过程中测量了20次的磨削力，选用磨削过程中稳定的10次力信号进行分析(顺磨力和逆磨力各5次)。取其平均值作为本次实验的磨削力。

利用激光位移传感器对加工过程中工件形状的变化进行跟踪测量。测量时，在工件前、中、后等3个位置各测量2次，通过平均得到工件的曲面轮廓。

2 砂轮表面磨粒的排布设计及制备

虽然学者们提出了各种不同的磨粒排布形式，但是总体而言，可以通过以下3个参数来确定磨粒的排布形式，即磨粒沿周向的排布参数(磨粒周向间距L)，磨粒沿轴向的排布参数(磨粒轴向间距C)以及磨粒的排布角度α。磨粒排布样式示意图如图1所示。其中最为关键的是磨粒周向间距L以及磨粒轴向间距C。本文中提出从单颗磨粒的最大切削厚度来确定磨粒的周向间距L；从2颗磨粒的相互干涉作用来确定磨粒的轴向间距C。

图1 磨粒排布样式示意图Fig. 1 Schematic diagram of abrasive grain arrangement style

2.1 周向间距L的选择

MARKIN[10]提出了单颗磨粒最大切削厚度hmax的概念。单颗磨粒最大切削厚度的大小不仅影响着磨粒所承受的载荷，同时也影响着磨粒的磨损。单颗磨粒最大切削厚度的计算方法如式(1)所示：

(1)

其中：vw为工件进给速度，mm/min；vs为砂轮线速度，m/s；ap为磨削深度，μm；ds为砂轮直径，mm；L表示磨粒的周向间距，mm。

从式(1)中可以看出：单颗磨粒最大切削厚度除了与工艺参数有关外，还与砂轮的直径和磨粒的周向间距L有关。对于平面砂轮，由于砂轮的直径不变，所以磨粒的周向间距也都相同；而对于曲面砂轮，由于其半径不同，要想保证单颗磨粒最大切削厚度相同，就需要建立砂轮直径ds和磨粒周向间距L的关系式：

(2)

式中：ω为加速度，rad/s。

当确定了磨削工艺参数，以及单颗磨粒最大切削厚度后，由式(2)可以计算出曲面砂轮表面不同曲率处的磨粒周向间距L。

2.2 轴向间距C的选择

磨粒周向间距L决定了单颗磨粒的去除体积，而磨粒的轴向间距C则决定了工件表面的材料是否会被完全去除。对于脆性材料而言，为了提高其材料去除率，可以充分地利用材料脆性裂纹扩展的特性。压痕实验表明：脆性材料发生脆性断裂时，其裂纹尺寸会大于压头的尺寸。当磨粒数量超过1颗时，相邻磨粒的断裂宽度就会发生干涉，因此控制好相邻磨粒的干涉程度，就可以很大程度上减少磨粒的使用，提高磨粒的利用率，见图2所示。

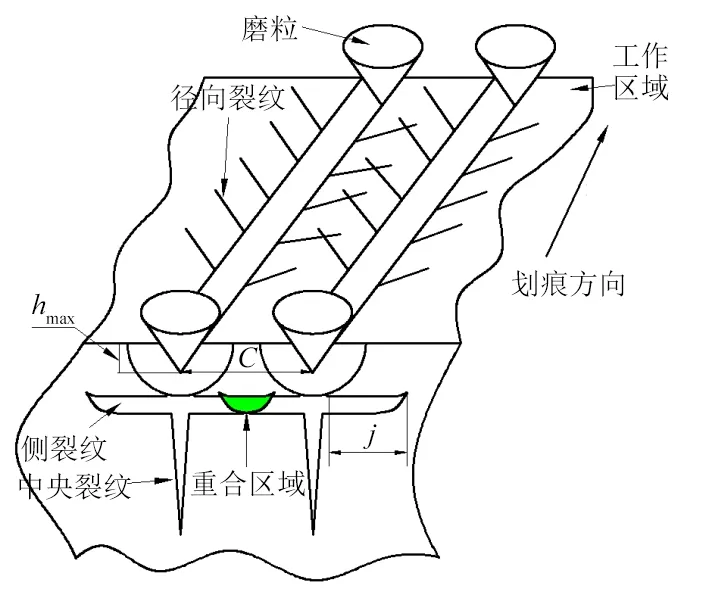
图2 压痕断裂图Fig. 2 Indentation fracture diagram

材料的断裂系数见式(3)所示[11]：

(3)

其中：KIC为材料的断裂系数，Pa·mm-1/2；H为材料的硬度，以维氏硬度计算；E为弹性模量，MPa；j为断裂宽度，μm；b为压痕宽度，μm。

根据图2可以看出：压痕宽度和断裂宽度之间存在一定的关系。一般假设磨粒为三角形截面，结合已经确定的单颗磨粒最大切削厚度值，可以得出：

(4)

其中：θ为三角形磨粒的顶角度数，其单位是°。

根据式(3)、式(4)可以得出断裂宽度j和单颗磨粒最大切削厚度hmax之间的关系，见式(5)：

(5)

当材料的物理特性(断裂韧性、维氏硬度、弹性模量)确定时，由单颗磨粒的最大切削厚度就可以确定磨粒的断裂宽度(图3)，进而设计其轴向间距C。

(a)压痕断裂力学 Indentation fracture mechanics(b)hmax与压痕的关系hmax vs indentation图3 断裂参数计算示意图Fig. 3 Schematic diagram of fracture parameter calculation

2.3 具体砂轮表面磨粒排布参数的确定

所选用的砂轮基体如图4所示。其直径从φ250 mm到φ242 mm变化。取初始L=10 mm，将相关参数及L的数值代入式(1)可以确定单颗磨粒最大切削厚度为1.26 μm。将上述参数代入式(2)可以确定不同直径处的磨粒周向距离，见式(6)：

L=0.002 529 822·d3/2

(6)

(a)曲面砂轮三维图 3D diagram of curved grinding wheel (b)CAD尺寸图CAD size drawing图4 砂轮形状尺寸Fig. 4 Shape and size of grinding wheel

由式(5)和图3可得磨粒的轴向间距C为12.56 μm。排布角度的变化也会导致加工弧区内磨粒数的变化。根据文献[12]的研究结果，选用α角为45°。

在保证所用金刚石颗粒数相同的条件下，将磨粒随机分布在砂轮表面制备尺寸相同的无序排布砂轮。

3 实验结果分析

3.1 磨削力随磨削过程的变化

图5所示是磨削力随磨削过程的变化。从图5中可以看出：随着材料去除量的增大，磨削力呈现上升趋势，与平面砂轮的磨损规律基本一致。逆磨时的磨削力要略大于顺磨时的磨削力。在磨削前期，磨粒有序排布曲面砂轮和无序排布曲面砂轮的法向磨削力基本一致，但有序排布砂轮的切向磨削力则略小于无序排布砂轮的。无论是顺磨还是逆磨，在材料去除量达到了1.4×106mm3后，磨削力出现急剧上升的趋势，且无序排布砂轮的法向力明显高于有序排布砂轮的；但两者的切向力则几乎相同。总体而言，无论是顺磨还是逆磨，有序排布曲面砂轮的磨削力总体上是小于无序排布曲面砂轮的。

(a) 顺磨FnFn in down grinding(b) 逆磨Ft Ft in up grinding(c) 顺磨FnFn in down grinding(d) 逆磨FtFt in up grinding图5 不同砂轮的磨削力与材料去除量的关系Fig. 5 Relationship between grinding forces and material removal of different grinding wheels

3.2 砂轮磨损随磨削过程的变化

在磨削过程中，磨粒会呈现出4种不同的状态，分别是完整、磨平、破碎和脱落，如图6所示。

实验中对曲面砂轮左边、中间和右边3个区域的磨粒状态进行统计，见图7所示。各不同区域的磨粒状态随磨削过程的变化如图8和图9所示。

(a) 完整Complete(b) 磨平Flattened (c) 破碎Broken(d) 脱落Falling off图6 砂轮表面金刚石磨粒的状态Fig. 6 States of diamond abrasive grains on wheel surface

图7 磨粒分区示意图Fig. 7 Schematic diagram of abrasive partition

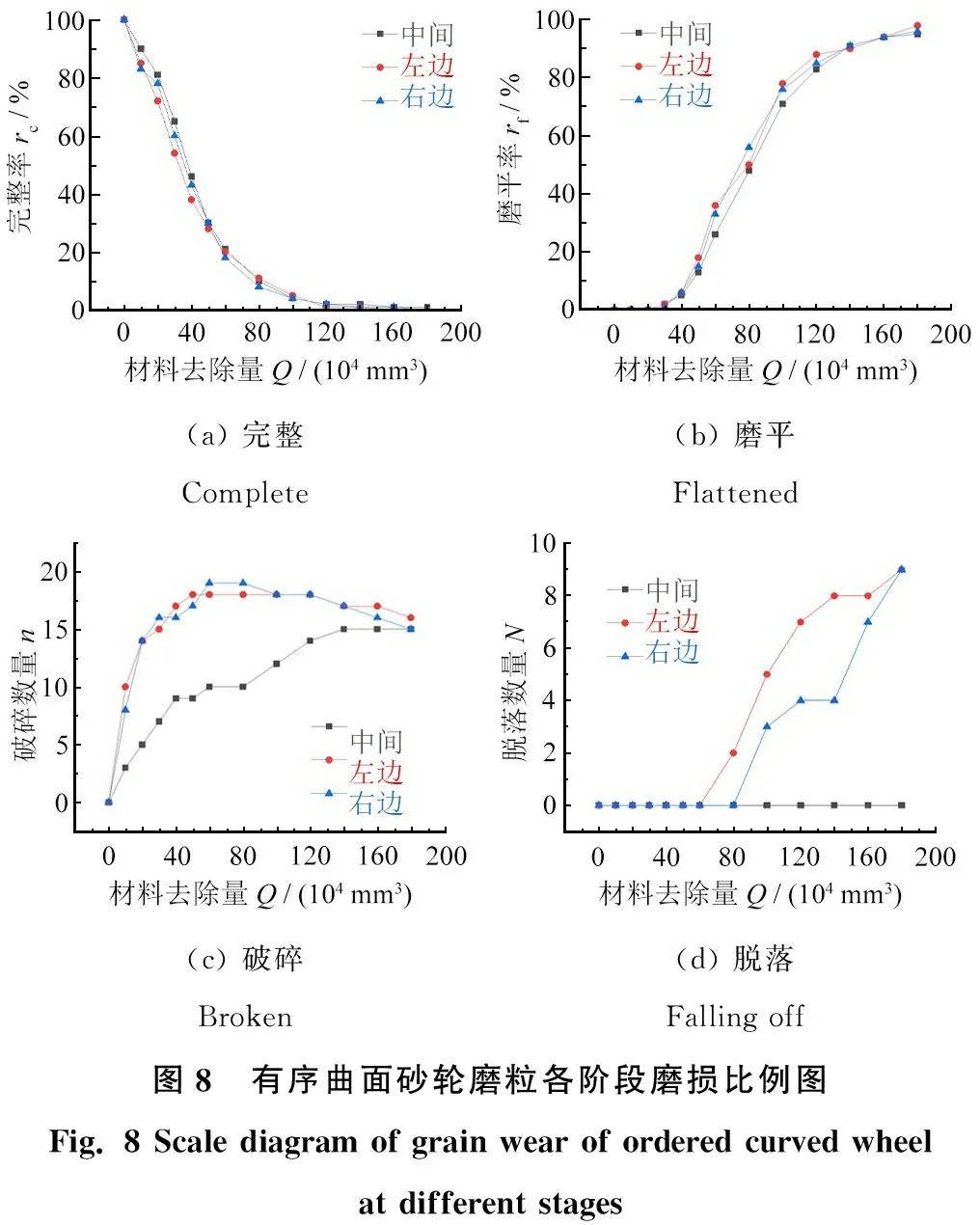
(a) 完整Complete(b) 磨平Flattened (c) 破碎Broken(d) 脱落Falling off图8 有序曲面砂轮磨粒各阶段磨损比例图Fig. 8 Scale diagram of grain wear of ordered curved wheel at different stages

从图8和图9可以得出：在砂轮磨削的过程中，磨粒逐渐被消耗，金刚石磨粒形成凸台，因此有序排布曲面砂轮和无序排布曲面砂轮最主要的失效形式是磨粒磨平(见图8b和图9b)。由于钎焊的高把持力，磨粒出现破碎或者脱落的状态只占磨粒总数量的很少一部分。在完整率方面，无序排布曲面砂轮大于有序排布曲面砂轮，这表明在参与磨削方面，有序排布曲面砂轮磨粒有效参与磨削的数量更多。在磨粒磨平率方面，有序排布曲面砂轮更大，这同样表明有序排布曲面砂轮参与磨削的磨粒数量更多。在磨粒破碎方面，有序曲面砂轮磨粒破碎数量更多。在磨粒脱落数量方面，有序曲面砂轮更低，这表明有序曲面砂轮寿命更长。总体而言，可以看出有序排布曲面砂轮的磨粒一致性优于无序排布曲面砂轮的。

(a) 完整Complete(b) 磨平Flattened (c) 破碎Broken(d) 脱落Falling off图9 无序曲面砂轮磨粒各阶段磨损比例图Fig. 9 Scale diagram of grain wear of disordered curved wheel at different stages

对比曲面砂轮各个区域的磨粒磨损占比可以发现：有序排布曲面砂轮3个区域的磨粒完整率和磨平率变化基本一致；破碎和脱落数量有所差别，两边破碎比较多、中间破碎相对较少，两边区域脱落基本一致、中间区域没有脱落。对于无序排布曲面砂轮而言，其完整、磨平和破碎各个区域变化趋势基本一致，但其在占比上却产生较大变化；在脱落方面，右边区域脱落数量多于其他2个区域的，且其变化曲线急剧陡峭。有序曲面砂轮和无序曲面砂轮磨粒最开始脱落的区域都是砂轮的两边位置。

3.3 工件形状误差随磨削过程的变化

以第一次磨削的形状作为起始点，通过对比后续测量的工件形状最大值与第一次测量的值，可以得到不同加工阶段的工件形状误差，其计算方式见图10所示。不同砂轮所加工出的工件形状偏差随磨削过程的变化见图11。

图10 形状误差计算方式Fig. 10 Calculation method of shape error

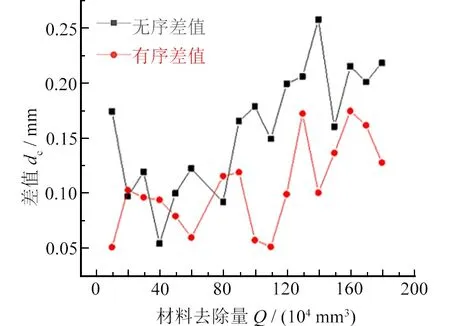
图11 工件形状偏差图Fig. 11 Workpiece shape deviation diagram

从图11可以看出：有序排布曲面砂轮和无序排布曲面砂轮的工件形状偏差都随着磨削加工过程的进行而增加。这说明随着材料去除量的增加，砂轮的磨损加剧，导致工件形状出现变化。由于砂轮不同位置处的磨损不同(见图8、图9)，工件顶端尺寸的变化程度也不同。对比有序排布曲面砂轮和无序排布曲面砂轮可以发现：有序排布曲面砂轮的偏差值明显小于无序排布曲面砂轮的，其形状精度平均提高了34%。这表明在相同材料去除量下，有序排布曲面砂轮磨粒磨损小于无序排布曲面砂轮磨粒磨损，有序排布曲面砂轮的磨削工件质量优于无序排布曲面砂轮的。

4 结论

提出一种曲面砂轮表面磨粒排布的设计方法，并通过有序排布曲面砂轮与无序排布曲面砂轮的对比磨削实验发现：同无序排布曲面砂轮相比，无论是顺磨还是逆磨，有序排布曲面砂轮的磨削总体上是小于无序排布砂轮的，其磨粒一致性更好，所加工的工件形状精度平均提高了34%。实验结果证实所提出的设计方法可以有效地用于设计曲面砂轮表面的磨粒排布。