吸力锚飞溅区吊装入水速度影响分析
昝英飞, 郭睿男, 韩端锋, 黄福祥, 罗超, 贾辉,3
(1.哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001; 2.海洋石油工程股份有限公司, 天津 300450; 3.哈尔滨哈船特装科技发展有限公司,黑龙江 哈尔滨 150001)
结构物跨越飞溅区通常被视为海上吊装作业的关键阶段。这一阶段主要影响作业安全的因素包括波浪、吊装速度、吸力锚的局部速度和运动幅值。由于结构物的水动力特性与形状和速度相关[1],所以在波浪的作用下结构物可能存在多自由度的运动,剧烈的水平面运动容易导致结构物与安装船碰撞。吸力锚在飞溅区的受力更为复杂,穿过飞溅区时砰击力只是入水力中的一部分,在其下降的过程中还存在出水力[2],反复变化的载荷加速了吊绳和起重机的疲劳,较大的突变载荷可能破坏吊绳和吸力锚。因为控制吊装速度能有效减小主要因素的影响,所以研究吊装速度和波浪对吸力锚吊装入水作业的影响十分必要。对海上吊装作业进行研究一般包括实船试验和模型实验以及数值分析方法。刘永林等[3]通过实船试验研究了海上作业的弱非线性ROV中继站缆索系统的运动和张力。Zan等[4]和周傲[5]通过模型实验研究水下模块的吊装作业,分析模块在波浪中的运动和受力。在数值研究方面,学者们基于运动仿真和时域仿真展开了大量研究。Ku等[6]开发了多体系统动态分析程序对多台起重机分段吊装的动态响应进行了研究,确定多台起重机在运行过程中的运动和动态载荷等动态效应。Li 等[7]对海上风机单桩吊装作业进行数值模拟,建立了桩—船耦合系统的数值模型,考虑了波浪衍射和辐射影响,研究安装船附近的扰动波浪场,比较扰动场下吊臂运动、缆绳张力和夹具接触力等关键响应。Sfteland等[8]研究水下框架结构进入飞溅区时产生的巨大水动力,和动态力造成的缆绳松弛或过载,确定了结构安全安装的最高海况,并提供了飞溅区圆柱体的水动力系数。Acero等[9]介绍了一种评估海上作业操作极限和可操作性的方法,基于该操作过程和数值分析方法,识别海上风力涡轮机和过渡件安装的关键事件及相应的响应参数,得到不同作业要求下允许的极限海况。Li等[10]在考虑了安装船的屏蔽效应和波浪传播方向的影响下,对海上风力发电机单桩的起吊过程进行了数值研究。使用海洋工程软件SIMO (simulation of complex marine operations) 和外部动态链接库在船舶附近预定义的位置之间进行流体运动学插值来研究船舶在提升过程中的屏蔽效应。Wang等[11]研究了海底管线的飞溅区吊装作业,从一系列不同方向和频率的规则波对吊装系统的影响入手,寻找吊装系统最大响应时的浪向和管线的浸没状态,并进一步研究该状态遭遇不同一维波浪时的最大缆绳张力。Wang等[12]建立浮吊—吊物耦合系统的水动力模型,计算浮吊和吊物在不同波高和周期波浪条件下的运动响应。在充分考虑了船舶稳性和适航性、人员舒适性以及设备安全性的基础上,通过比较浮吊与起吊物的摆动和加速度幅值,确定浮吊作业的极限波高和起吊作业周期。Li等[13]利用基于多体系统动力学、虚拟现实技术以及允许多个工作人员共同操作协同仿真的集成方法,研究利用浮式起重机和履带起重机共同执行的海底模块翻转作业。Li等[14]对大型水下管线的飞溅区吊装作业进行了数值模拟和分析,比较不同波陡、方向和不规则波的分解数量对极端响应概率的影响,计算了下降过程的砰击载荷和入水载荷。进行大量的时域模拟,以评估操作标准,包括:缆绳的松弛、破断载荷以及管线与船之间的间隙。Chilinski等[15]提出了一个3自由度的基于结构物和船舶双向波浪激励计算并考虑补偿器的提升作业模型,研究规则和不规则波下作业的响应。在计算流体力学 (computational fluid dynamics, CFD) 方法方面,文献[2,6]通过软件 ANSYS CFX 模拟吸力锚和采油树的单自由度运动,对其水动力进行研究,并利用时域仿真进行吊装作业的研究。Filip[17]利用开源工具OpenFOAM通过对极端波浪的模拟,研究结构物在飞溅区的砰击。
在利用模型实验方法进行飞溅区吊装作业的研究时,采集的数据种类有限,而且缺少对波浪和流动的细致记录,而实船试验成本较高,且海洋环境复杂。本文利用CFD方法,在前期的吸力锚[18]和板架式结构物吊装入水研究[4,19]的基础上,研究考虑波浪环境时,吊装速度对吸力锚的运动和缆绳张力的影响,利用实船采集的实测数据与数值计算结果进行对比验证。通过定义与波浪过零周期有关的浮动动态放大因子和动态影响,排除吸力锚静载荷的干扰,研究不规则波对吊绳拉力的影响。分析吊装速度对张力和结构物的六自由度运动的非线性和非对称性影响。
1 结构物吊装模型建立
图1所示结构物模型与实物的比例尺为1∶2,该结构物由4个吸力锚和一组钢管焊接成的钢架构成。结构物模型高H为6.65 m,宽B和长L均为13.9 m,空气中质量26.25 t;吸力锚直径3 m,高2.75 m,锚壁厚0.01 m,设有2个通风孔直径分别为0.305 m和0.51 m,通气孔布置并非对称。吸力锚顶采用对称布置的肘板加强。重心距结构物底端3.281 m,随体坐标原点位于重心G,Gx轴正方向沿纵向,Gy轴沿横向,Gz轴沿垂向向下。固定坐标系Ex0y0z0位于重心正下方与吸力锚顶部的上表面等高的平面上,坐标轴方向与随体坐标一致。工况1~7的吊装速度v分别为:0.07、0.141、0.212、0.283、0.354、0.424和0.495 m/s,基于傅汝德数对应工程作业速度为0.1、0.2、0.3、0.4、0.5、0.6和0.7 m/s。

图1 吸力锚几何模型Fig.1 Geometry of suction anchor
计算域的尺寸和随体坐标系如图2(a) 所示,计算域两侧为对称面,前部和顶部为速度入口,后部和底部为压力出口,自由液面在结构物底部以下0.25 m处。吸力锚周围区域采用动网格,该区域长和宽为38.5 m,高17.35 m。计算域中的所有部分均为6面体结构化网格,为保证计算域中没有过小的网格,均采用吸力锚的长度进行定义[20]。网格目标尺寸3.2 m,最小0.1 m,采用自适应网格对动网格周围和自由液面进行2层加密。该加密方式可使动网格周围的背景网格尺寸与动网格区域一致,自由液面自适应细化之后的网格尺寸小于波高的 10%,动网格的边界距离结构物为4倍目标网格距离,网格共计601 451个。
吸力锚在吊装过程中进行6自由度运动。在当下网格设置中,不同吊装速度仿真的y+最小255.8,最大为299.6,每一组仿真的y+均在30~300,所以网格设置合理[21]。
本文计算基于雷诺时间平均Navier-Stokes(Reynolds-Averaged Navier-Stokes, RANS)方程。流体在时间t内的控制方程为[22]:
(1)
(2)
(3)
本文应用k-ω湍流模型和双层全y+壁面函数(two-layer ally+wall treatment),采用流体体积函数法(the volume of fluid,VOF)求解多相流。模拟在结构物顶部距离水面1 m以下后停止,计算步长为Δt=0.01 s,此时以0.495 m/s为吊装速度的模拟中库朗数为0.05。计算机的CPU为Intel(R) Xeon(R) CPU E5-2640 v4@2.40 GHz,采用并行运算,单个模拟时间约为79 000 s。
2 结构物吊装数值结果与分析
2.1 数值结果的验证
为验证数值结果的准确性,将吸力锚吊装的数值结果与Bertelsen[23]进行的工程实测结果进行对比。图3为数值计算和实测的波浪时历比例尺为1/2的结果,波浪的时历从吸力锚触水开始,波浪沿Gx轴负方向传播,在各个速度下结构物遭遇波浪的初始位置相同。从图中可以看出数值计算结果与实测结果基本吻合。

图3 波浪时历Fig.3 The time series of wave
图4为吊装速度为0.07 m/s,比例尺为1/2时的数值和实测的缆绳拉力和结构物重心的垂向位移z和ztest对比。初始时刻吸力锚触水,缆绳拉力的数值结果和试验结果变化规律相似,极大值和极小值发生时刻和幅值相近;数值结果的拉力FT最大为281 742.111 N,最小168 526.198 N;实测结果的拉力FT,test最大284 137.658 N,最小178 293.117 N,数值结果与实测结果分别相差0.84%和5.48%;0~50 s内吸力锚重心的垂向速度平均值数值结果为0.069 1 m/s,实测结果中为0.071 9 m/s,相对误差为3.89%。结果表明,数值结果与实测结果基本吻合,从而证明本研究的数值方法能准确模拟吸力锚在飞溅区的吊装作业。
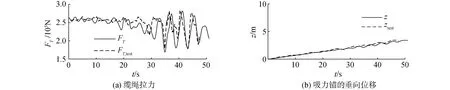
图4 缆绳拉力和吸力锚垂向位置的数值与实测结果对比Fig.4 Comparison of the numerical cable tension and the vertical position of suction anchors with the measured results
2.2 波浪对缆绳拉力的影响
如图4(a)所示,缆绳拉力在波浪的作用下出现明显振荡。在发生最小拉力前,存在多个幅值较大且逐渐增加的波动,这说明随着吃水的增加吸力锚受波浪的影响逐渐增强。在最小拉力之后,由于吸力锚完全入水,结构物所受的波浪力快速减小,所以缆绳的拉力振荡衰减。在吸力锚经过飞溅区的最后阶段,由于钢架和吸力锚仍然受到表面波浪和次波面水动力作用,缆绳拉力依然存在较大幅值的振荡。
为研究波浪对缆绳拉力的影响,本文引入浮动动态放大因子(dynamic amplification factor,DAF)和动态影响因子(dynamic effect, DE)[2],各个离散时刻的动态放大因子DAFi的计算方法为:
(4)
式中:N为样本总数;FTi和FTj为离散的缆绳拉力;2n个临近FTi的离散拉力FTj与FTi的平均值为稳态拉力。本研究中n的确定方法为:
(5)
式中T0为波浪的过零周期。
根据DAVGL规范[24],动态影响因子小于0.9时缆绳不会发生松弛,也不会发生突变载荷。动态影响因子DEi为:
DEi=DAFi-1
(6)
图5表示0.141、0.283和0.424 m/s为吊装速度时的DEi。随吊装速度的增加,在发生最小DEi前经历的较小谷值个数减少。由于每种速度的模拟中使用相同的波浪,所以DEi的峰值和谷值发生的时刻相近。
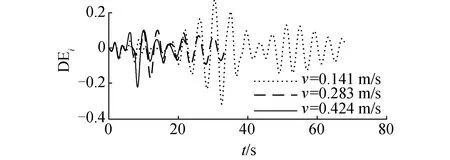
图5 浮动动态放大系数Fig.5 The floating dynamic amplification factor
图6为DEi的最大值DEimax和最小值DEimin随傅汝德数Fr的变化,DEimax和DEimin关于0近似对称并随速度非线性变化,但随速度增加对称性变差。其中DEimax最大0.274,最小0.090;DEimin最大-0.136,最小-0.336。所有工况下的DEi均小于0.9,所以在此波浪条件下,各个速度的吊装作业缆绳均不会发生松弛,缆绳也不会产生突变载荷。
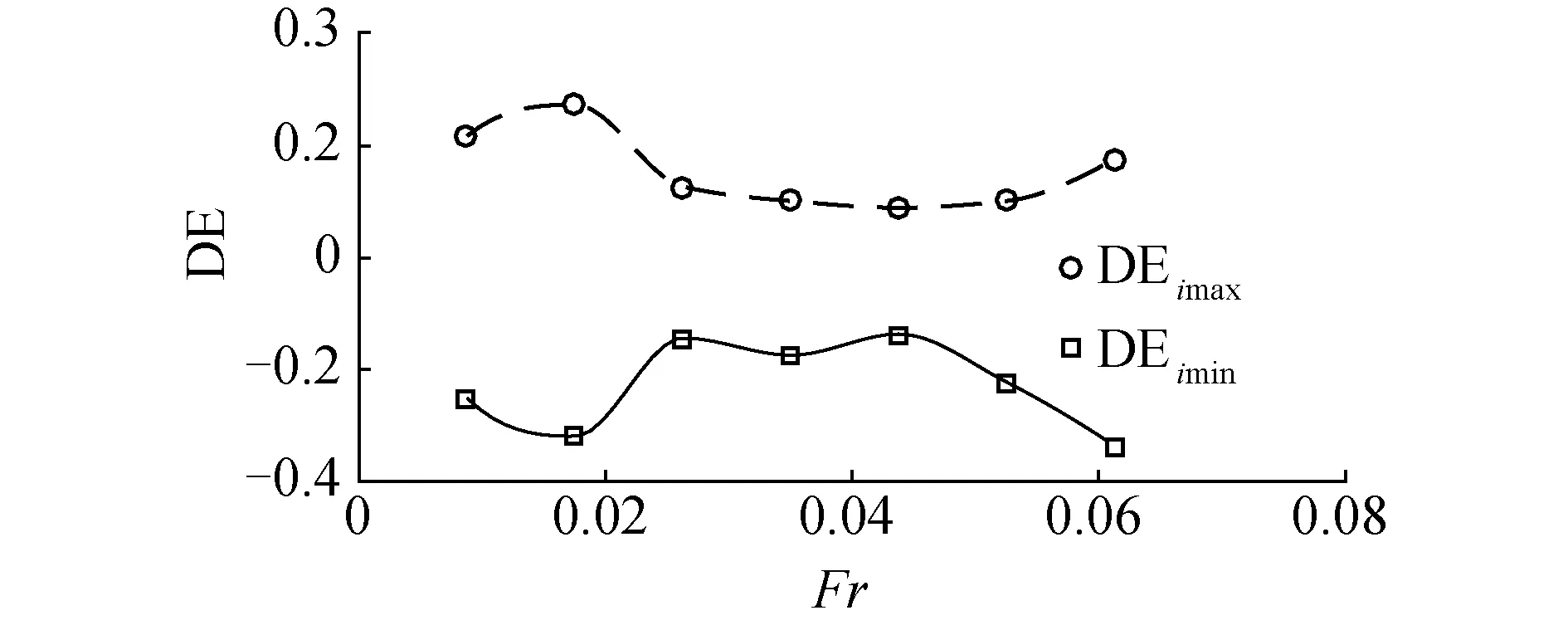
图6 DE的最大和最小值随Fr的变化Fig.6 The variation of maximum and minimum DE with Fr
各吊装速度下发生最大和最小DE时的自由液面高程如图7所示,图中静水面的高度为0。吸力锚后部的波浪发生严重变形,水面高度变化滞后。当出现DE的最大值时,吸力锚处在波谷附近,当出现DE的最小值时,吸力锚处于波峰附近。当吊装速度为0.07 m/s并出现最大DE时,吸力锚并未浸没水中。

图7 最大和最小DE时自由液面形状Fig.7 The shape of water surface at the moment of maximum and minimum DE
0.212 m/s和0.354 m/s这2组工况在发生最小DE时结构物的吃水很深,锚顶距离水面较远,其他工况在发生最小DE时,锚顶接近液面或通气孔出现射流。所以,吸力锚的吊装作业中最小动态载荷和最可能发生缆绳松弛的时刻不一定发生在锚顶淹没时。在现有的吊装速度中,由于缆绳没有发生松弛,最大动载荷不一定发生在最小动载荷之后。
2.3 吊装速度对缆绳拉力的影响
各个速度下缆绳拉力的最大值FTmax和最小值FTmin如图8所示。缆绳拉力的最值随吊装的速度增加呈非线性变化,FTmax在工况3~6时变化较小,FTmax最大289 742.213 7 N,是重力的112.52%;FTmax最小263 643.075 N,是重力的102.38%。FTmin在工况5以后快速减小,FTmin最大179 911.638 N,是重力的69.87%;FTmin最小为117 975.354 N,是重力的45.81%。
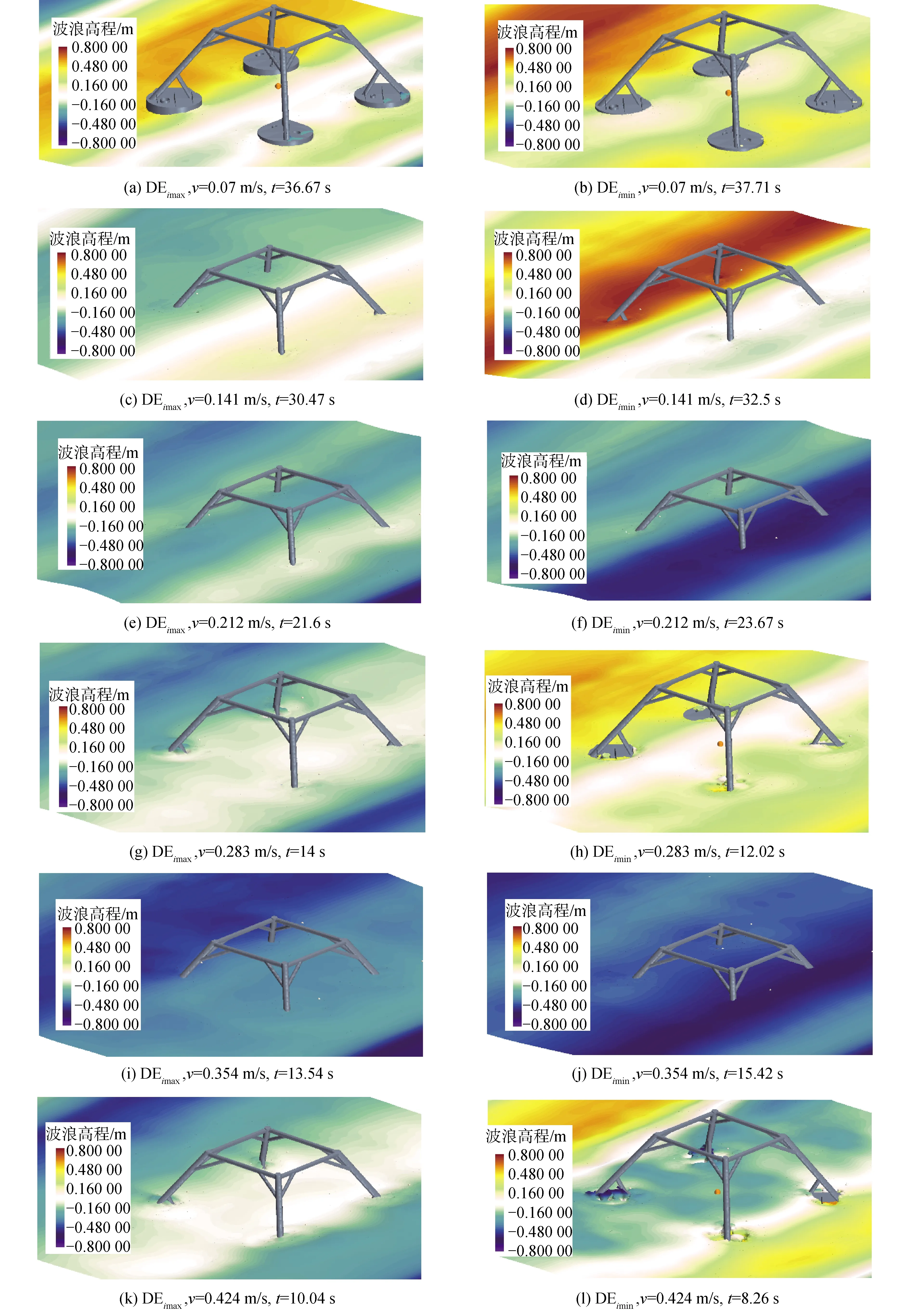

图8 拉力的最值Fig.8 The maximum and minimum of tension
为进一步反映拉力随速度的变化,对缆绳拉力的最值进行无因次化:
(7)
式中:CT为拉力系数;ρ为水的密度;A为吸力锚的水平投影面积;CT如图9所示。
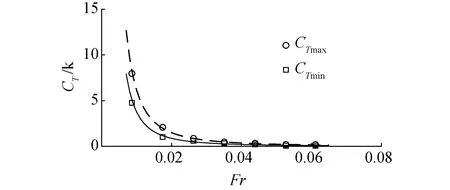
图9 拉力系数Fig.9 The coefficient of tension
最大拉力的拉力系数CTmax和最小拉力的拉力系数CTmin均随速度的增加而非线性减小。分别对CTmax和CTmin进行拟合后得到
CTmax=0.513Fr-2.039
(8)
CTmin=0.233Fr-2.103
(9)
2.4 吸力锚入水时的运动
图10表示吊装速度为0.141、0.283和0.424 m/s时结构物的运动时历。在吊装过程中结构物的纵向和横向位移(x和y)先出现低频大振幅的往复运动和高频的小振幅振动,并且往复运动振幅逐渐减小,其周期大于各时段波浪的过零周期。随着吊装速度的增加,往复运动的周期增加。垂向位移z的振荡随着吊装速度的增加而减弱。横倾角与纵倾角(φ和θ)的大振幅往复运动不明显,小振幅的振动频率随吊装速度变化较小,艏摇角γ的低频大幅值往复运动明显,且幅值随速度增加而减小。
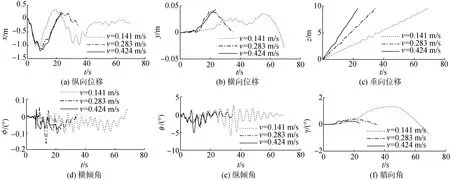
图10 结构物位移和倾角时历Fig.10 The time series of translations and orientations of the structure
图11为结构物重心处的纵向和横向位移,以下讨论中数值的正负仅为方向的标定。结构物的位移和欧拉角随速度呈非线性变化。随着吊装速度的增加,艏向的位移Xmax逐渐减小,艉向位移Xmin逐渐增加,平均纵向位移Xmean均小于0且逐渐增加,吊装速度越大,纵向位移受波浪的影响越大。结构物沿波浪方向运动剧烈,所以Xmax在相同吊装速度时小于Xmin。其中Xmax和Xmin最大分别为0.432 m和-1.310 m,均小于结构物长度的11%,Xmean最大为-0.817 m。
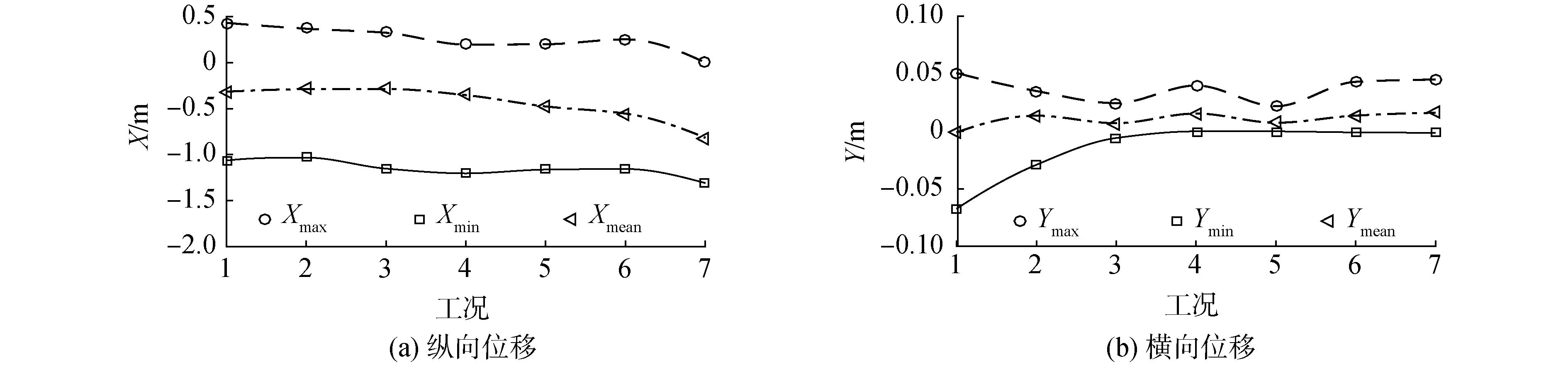
图11 结构物位移的极值和平均值Fig.11 The maximum, minimum and mean translation of the structure
结构物右侧和左侧的横向位移(Ymax和Ymin)和平均值Ymean也随速度非线性变化。除工况1和2外,其他工况的Ymax均大于Ymin,而且当速度大于0.212 m/s时,右侧的横向位移逐渐减小至0附近,所以Ymean此后均大于0。Ymax和Ymin最大分别为0.050 6 m和-0.067 4 m,均小于结构物宽度的0.5%。虽然吸力锚的布置关于重心中心对称,但结构物在波浪中的横向运动的对称性较差,这可能与结构物的艏摇运动相关。各个速度时的位移均小于1.5 m,所以该结构物的飞溅区作业中不易与安装船发生碰撞。
如图12所示为7种工况下结构物横倾角φ、纵倾角θ和艏摇角γ的最大值(φmax、θmax和γmax)、最小值(φmin、θmin和γmin)和平均值(φmean、θmean和γmean)。从图12(c)中可知,结构物在经过飞溅区时发生艏摇,这是因为吸力锚的通气孔并非对称分布,在波浪的作用下会发生非对称载荷,这一运动也会影响结构物的横向位移。结构物的欧拉角随吊装速度呈非线性变化,随着速度的增加,横摇角和纵倾角的平均值(φmean和θmean)逐渐增加,这说明吊装速度越大横摇和纵摇越剧烈且非对称性越明显;相反的是,艏摇角的平均值γmean逐渐减小并接近0°,所以吊装速度越高艏摇角越小。左倾φmin最大-0.267°,右倾φmax最大0.210°;艏倾θmin最大-5.821°,艉倾θmax最大2.970°;艏摇角最大4.897°,朝向右侧。
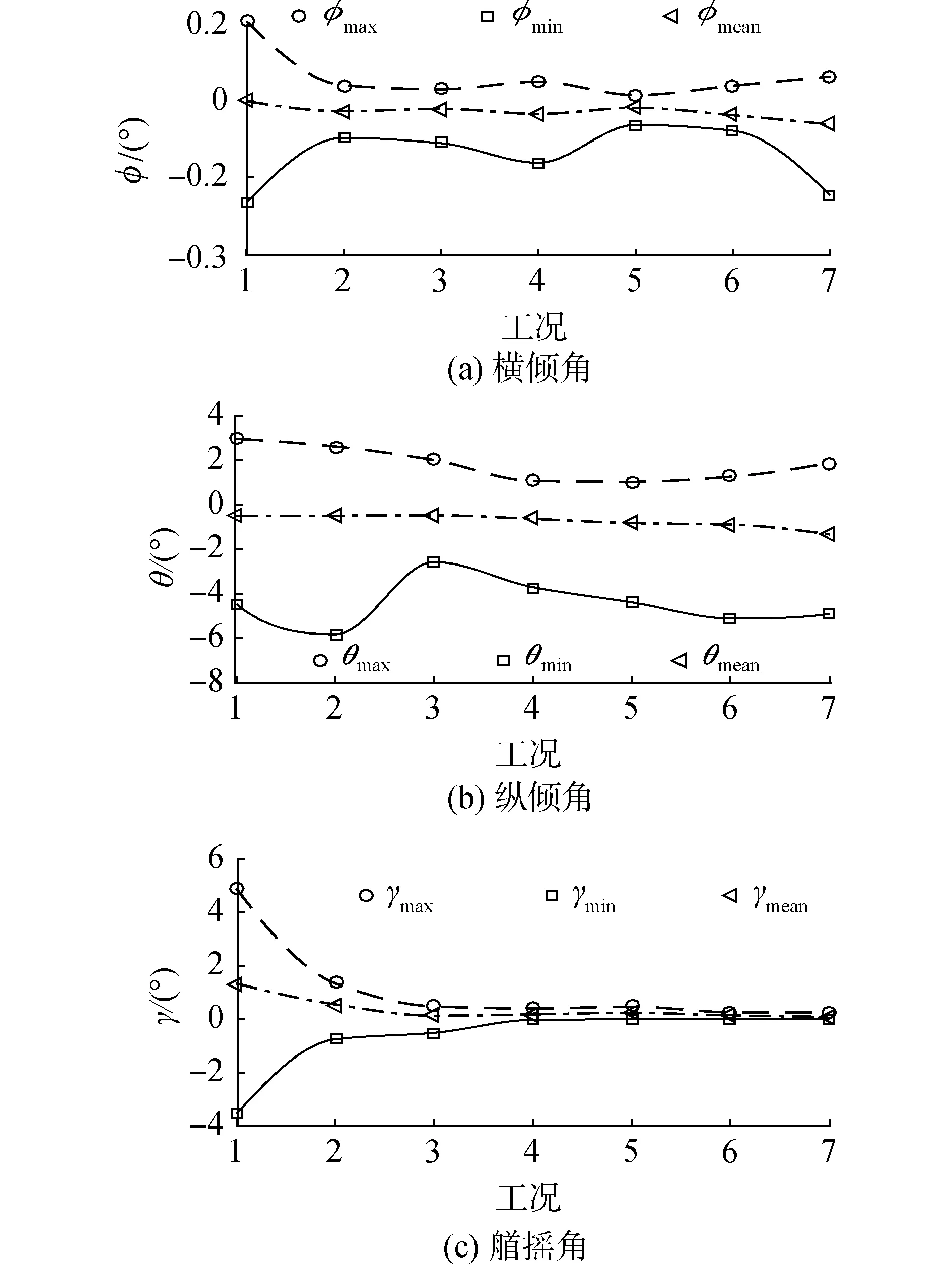
图12 结构物欧拉角的最值和平均值Fig.12 The maximum, minimum and mean Euler angle of the structure
3 结论
1)吊装速度小于0.7 m/s时吊绳不会松弛且吸力锚位移较小,所以该速度以下进行吊装作业是安全的。在飞溅区进行吸力锚的吊装作业时,缆绳拉力和结构物的运动状态将受到波浪的严重影响,随着吊装速度的增加,最大拉力系数随傅汝德数的增加而非线性减小,吊绳拉力和结构物的运动状态呈现非线性和非对称性响应。
2)与大多数完全对称的结构物不同,由于工程使用的吸力锚通气孔并非对称分布,其在吊装过程中发生艏摇,艏摇运动会影响结构物的横向位移,而吊装速度越高,吸力锚的艏摇角越小。吸力锚的纵向和横向运动存在低频大幅值的往复运动和高频小幅值的振动。
在进行类似该结构物的飞溅区吊装作业仿真时仅考虑结构物的垂向运动是不合理的,应当充分考虑结构物在水平方向的运动。对于有非对称结构的结构物,应关注各自由度运动的非对称性以及艏摇运动。本研究的结果对设计吸力锚和计划吸力锚的吊装作业具有一定的参考价值,由于本研究时间有限,波浪传播方向和船舶运动的影响将在未来进一步研究。

