人致振动载荷下楼盖结构的瞬态动力学分析
付章建, 岳祖润
(1.石家庄铁道大学 土木工程学院,河北 石家庄 050043; 2.河北省建筑科学研究院有限公司,河北 石家庄 050021; 3.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043; 4.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室,河北 石家庄 050043)
随着建筑行业的不断发展,工程师在设计建筑结构时,综合考虑了建筑结构的安全性、适用性、耐久性、美观性等因素的影响,使设计出来的结构可以满足工程的基本需求。但是,在使用过程中有时会出现由于建筑物振动过大,使得建筑物在使用年限内出现由于共振引起的安全性问题。因此,近年来人们对建筑结构在服役期间的振动问题进行了广泛研究,尤其是人致振动作用下的桥梁结构[1-3]和大型公共场所楼盖结构,世界各国普遍采用健康监测的方法实时监测建筑物状态,并通过主动或者被动控制方式对建筑结构产生的振动进行控制[4-7],保证建筑物在使用期限内的安全性。学者们在结构动力学方面进行了深入的探索,取得了丰硕的成果。文献[8-10]从舒适度方面提出了改进的方法,提高了人行桥的振动舒适度;文献[11-14]通过数值仿真,分别对过街天桥、登机桥、地板、人行过道结构进行了计算分析,总结了所研究结构的人致振动规律;De[15]通过实验方法揭示了在各种人致荷载作用下,复合材料楼板的动力性能;文献[16-21]采用多种人致振动激励方式,对引起的楼盖振动响应的影响因素进行分类分析;An等[22]对弦支组合楼盖结构进行了人致振动分析,并进行了多载荷工况下的的现场试验,表明该结构受到多种载荷作用明显。上述研究多局限于对整个建筑结构的简单理论求解或者模态分析,对结构中楼盖各个响应点的动力特性研究分析相对较少,而工程中不同使用功能的楼盖对于结构动力特性的要求不尽相同,结构的响应规律也各异。
本文以河北省衡水市桃城区某小学体育馆为工程实例,通过实验测试和有限元验证的方法,以一层楼盖局部混凝土楼板为研究对象,采用人致振动激励,通过单点拾振获取所测楼板各测点的振动响应速度,分析在跳跃和屈伸运动激励作用下的楼盖动力学速度响应情况,对比并总结了2种工况下楼板的能量传递形式、机理及其响应规律。
1 测试楼盖结构及实验设计
本次测试结构为河北省衡水市桃城区某小学体育馆楼盖,该结构为地上2层的混凝土框架结构,一层为梁板式楼盖,平面布置图如图1所示。本次测试区域为楼盖中部区域,测试区域横向跨度10.35 m,纵向跨度15 m,横向主梁截面尺寸为300 mm×650 mm,纵向主梁、次梁截面尺寸均为250 mm×600 mm,柱子截面尺寸均为400 mm×400 mm,楼板为现浇楼板,厚度为110 mm,结构梁、板、柱混凝土强度等级均为C30。

图1 一层楼盖平面布置Fig.1 The plane layout of the first floor
楼盖结构响应作为结构分析的一个重要特性,能够系统地反映整个楼盖的各项指标,通过对各个指标的详细分析,可以对楼盖的动力学性能进行预测,判断楼盖结构的振动特性,进而可以从减振角度实现优化结构形式的目的。通过楼盖的结构动力响应实验分析,可以得到楼盖各个位置处的速度值,进而可以验证理论计算结果准确性。
楼盖板构件作为连续弹性体,当在不同位置进行激励时,响应各点的振幅不同,往往从激励点向周围呈辐射状分布。为了准确测量响应信号,振动测试方向应与结构楼板的垂直方向(法向)一致,将测点在沿横梁和纵梁方向上,分别等间隔布置。对于板构件的振动测试,测点数量不应少于5个,通过同步测量14个测点的响应,对比不同激励状态下楼盖结构的动力学响应规律,以期得到良好的测试效果,1~14号测点布置图如图2所示。
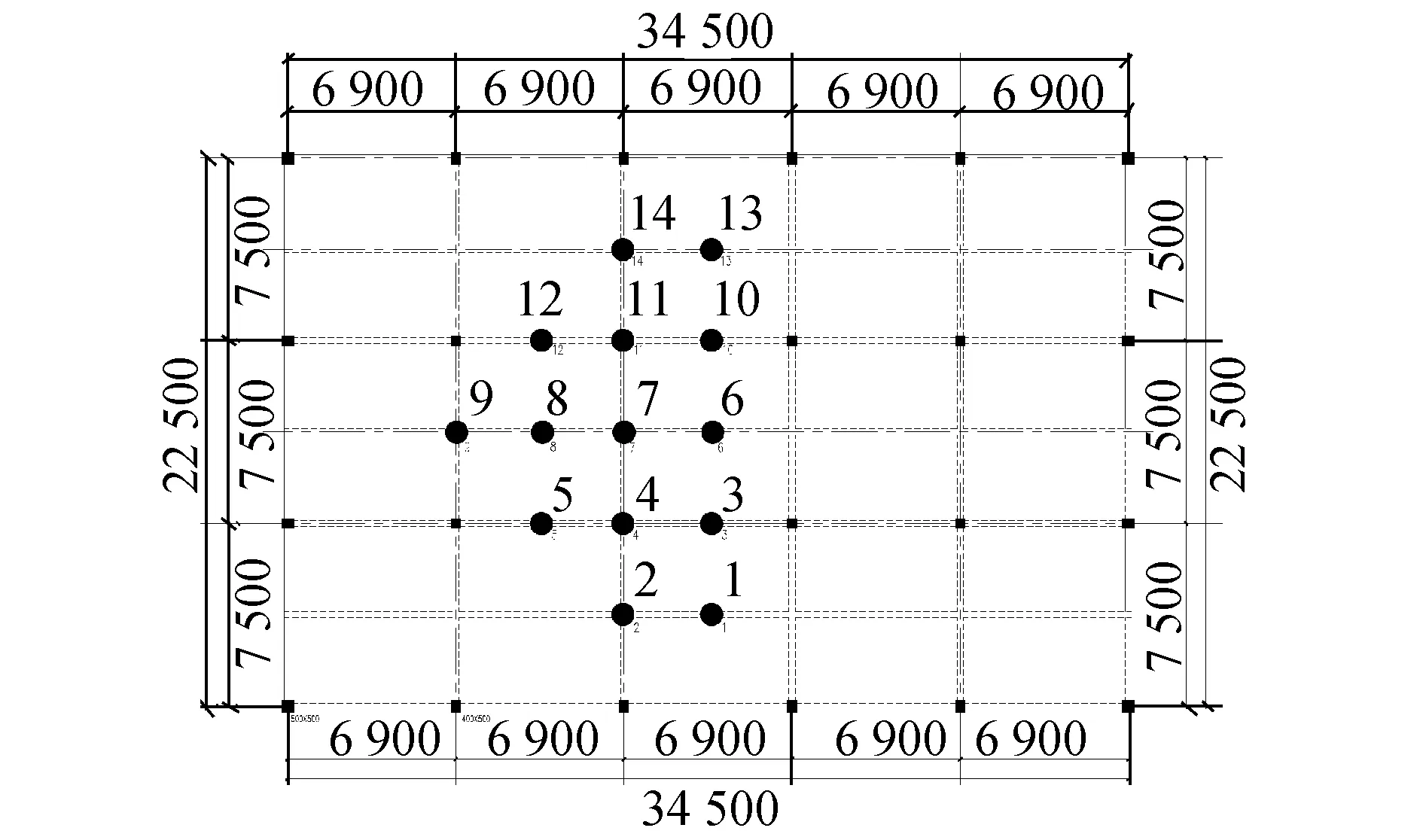
图2 测点布置Fig.2 The plane layout of the test point
本次实测用到的仪器设备主要有:16通道东华(DHDAS-5921)动态信号采集分析系统1台、100 m的2×0.3RVVP信号屏蔽线、东华2D001VDH610V速度传感器及信号接收软件等。其中,速度传感器灵敏度指标在(0.33~0.37 V/(m·s-2)),可以满足对楼盖结构测试信号要求。
每组测试时间为25 min,数据采集频率为0~100 Hz,采集完成后通过数据采集器对数据进行初步分析整理,分析不同激励状态下楼盖的响应情况,从而得到楼盖在不同时刻的速度变化情况。
2 有限元分析及约束条件
2.1 瞬态动力学理论
瞬态计算采用瞬态动力学平衡方程,将离散的有限元模型进行数值计算,得到不同时刻下的动力学响应,基本计算方程为:

(1)
式中:F(t)为外加激励作用;M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;u为位移变量。
瞬态求解过程需要进行差分计算,其中最常用的方法为Newmark有限差分方法,在一个时间间隔内有:
(2)
(3)
式中:u为位移变化量;α、β为Newmark积分参数。
需要对下一时刻的位移un+1进行求解,对式(2)、(3)进行整理得:
(4)
(5)

将方程(4)、(5)与方程(1)联立可以求解出随时间变化的瞬态动力学响应参数。
外加激励F(t)则根据实验速度激励信号,通过傅里叶级数方法进行拟合,傅里叶级数的基本公式为:

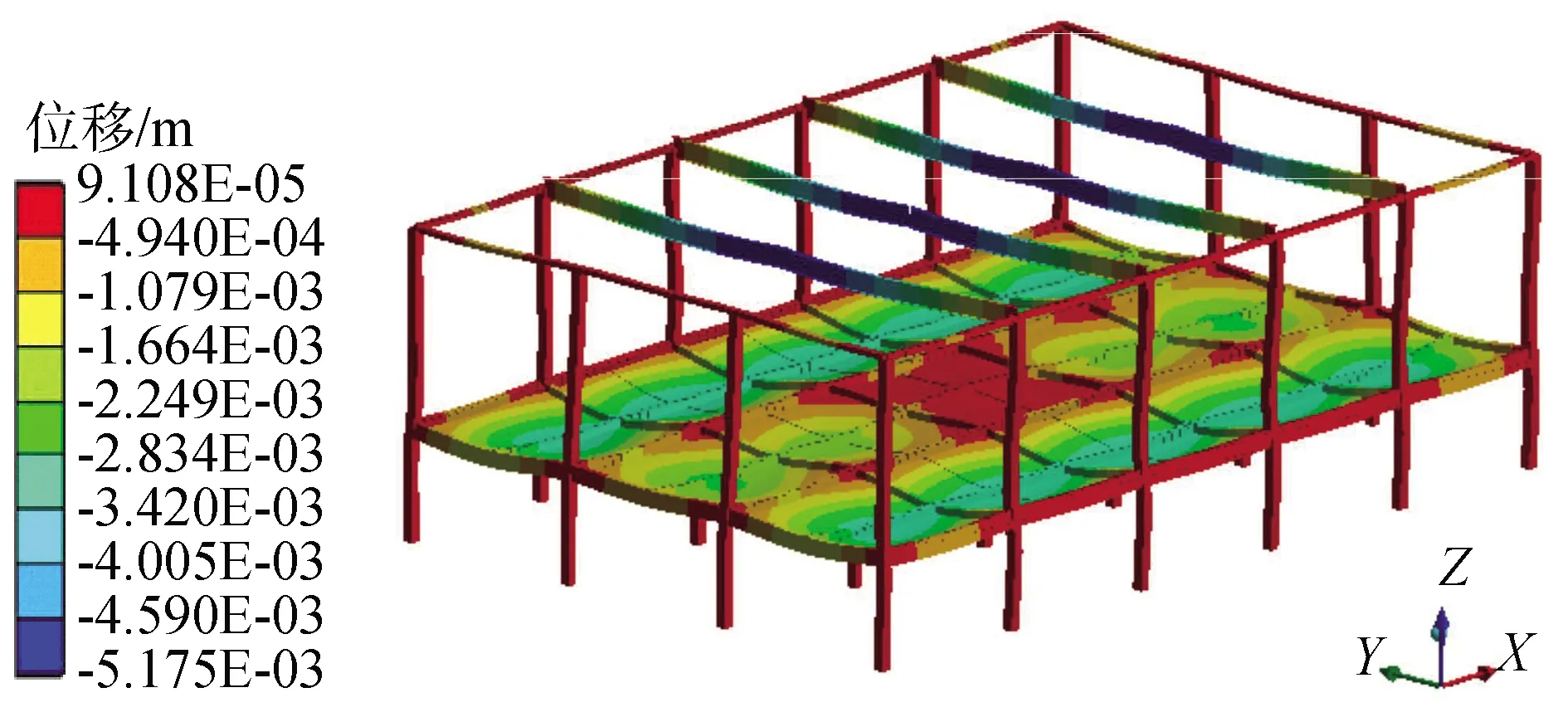
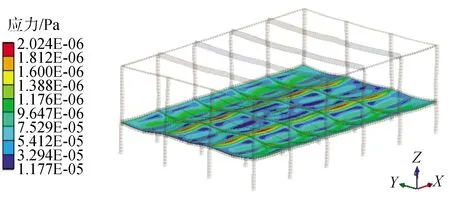
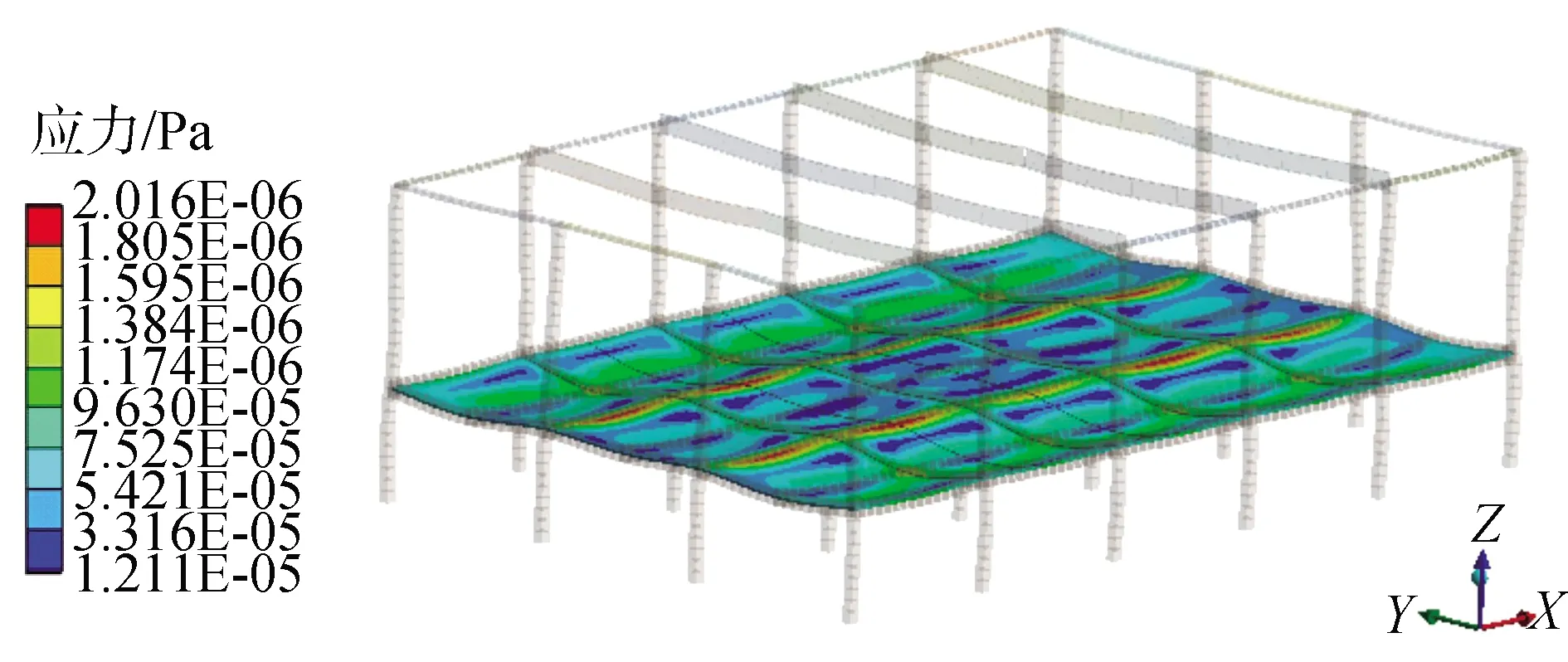
-π (6) 傅里叶级数可以对周期性函数进行准确的描述,展开的项数越多,拟合结果越精确,本文采用了8项展开式分别对跳跃和屈伸激励实验数据进行拟合,得到速度激励函数: f(t)=a0+a1cos(wt)+b1sin(wt)+a2cos(2wt)+ b2sin(2wt)+a3cos(3wt)+b3sin(3wt)+ a4cos(4wt)+b4sin(4wt)+a5cos(5wt)+ b5sin(5wt)+a6cos(6wt)+b6sin(6wt)+ a7cos(7wt)+b7sin(7wt)+a8cos(8wt)+b8sin(8wt) (7) 经数值拟合,跳跃激励时,ω为13.4;屈伸激励时,ω为6.78,傅里叶级数多项式的系数如表1。2种激励函数通过数据拟合得到的激励曲线如图3所示。 表1 2种激励下傅里叶拟合系数 图3 2种激励速度拟合曲线Fig.3 Velocity fitting curves of two excitation 将速度激励函数施加到数值仿真过程中,结合有限元方法对楼盖进行瞬态动力学响应分析,并与试验结果进行对照,验证速度激励函数作用下有限元模型分析过程中所引入的一系列理论参数是否符合实际情况,结构的动力响应是否符合实际要求,并进一步分析动力学响应的规律。 为了精确分析楼盖的瞬态振动响应,本次采用楼盖整体建模的方式,比较全面地考虑了楼盖结构在整个建筑结构中的实际约束,利用ANSYS软件建立三维有限元模型进行瞬态动力学分析,采用2节点BEAM188单元模拟梁单元,4节点SHELL181单元模拟板单元,采用自适应网格划分六面体单元,有限元模型见图4。 图4 ANSYS 模型Fig.4 The model of ANSYS 为了精确模拟结构的动力响应特性,取混凝土密度为2 500 kg/m3,弹性模量为3.0×1010Pa,泊松比为0.2,混凝土板的阻尼取为0.05,本次有限元动力学分析采用瞬态动力学分析方法。 为了全面分析模型的动力学特性,约束条件保证支撑柱体结构与地面相连的部分为固定约束,梁、柱、板之间为固定约束,瞬态动力学分析时,计算方法采用完全法分析,该法适用于大型有限元模型瞬态动力学分析,并且可以允许各种类型的非线性现象,准确分析瞬态动力学结果。 通过单人激励作用,分析了在不同激励形式下楼盖的响应规律及楼盖的响应机理,总结了楼盖的能量传递规律和响应形式。 实验过程中采用的单人激励形式包括跳跃运动和屈伸运动,激励点位于6号测点位置;仿真过程通过实验拟合出来的跳跃和屈伸2种形式的激励函数,作用到6号测点位置,对比分析楼盖结构14个测点位置的速度响应,分析在跳跃和屈伸运动2种激励形式下各测点的动力学响应特性和能量传递分布规律。 把6号测点作为单人运动激励点,激励方式为跳跃运动时,得到实验和有限元14个测点的速度响应信号如图5所示,对比分析实验测试和有限元结构测点的信号可以看出,各个测点速度响应表现出相同的规律,即6号激励点速度幅值最大,此处为能量输入位置;其次,在1、3、7、8、10、13号测点响应速度幅值在0.5 mm/s左右,2、4、9、11、14号测点响应速度幅值在0.2 mm/s左右,5、12号测点响应速度幅值分别在0.1 mm/s和0.05 mm/s。速度响应信号的大小反映了能量传输路径上能量的分布情况。首先,作为激励位置的6号测点,其响应为规则的跳跃运动信号,以此作为振动中心,能量首先传到其相邻的3、7、10号测点,而7号测点响应信号稍微小于3、10号测点,这是由于6号到7号测点之间存在横梁,增加了质量阻尼,传递能量下降;其次,在次相邻的1、8、13号测点速度幅值相对于相邻测点有所减小,同时由于横梁的阻尼作用,8号测点的速度幅值相对于其他2个测点有所减小;再次,随着测点位置远离激励点位置,传递到2、4、9、11、14号测点能量继续降低,最大速度减小到0.2 mm/s左右;最后,位于5、12号测点位置的响应速度最小,这是由于能量在传递过程中经过了立柱横梁的阻隔,消耗了大部分的能量。 图5 6号测点跳跃激励时14个测点速度响应Fig.5 The speed response of 14 points under the jump excitation of No.6 point 能量的传递是以激励点作为中心向四周传递到各个测点,但是能量的传递受到路径的影响。从整体上看,2种方法得到的各个测点表现出相同的能量分布和传递形式,但有限元分析是一种理想模型分析,得到的结果更加规律,而实验分析的数据则受到各种因素的影响往往出现数据分布的不均匀现象。 将6号测点的单人激励变为屈伸运动,采集实验和有限元14个测点的速度响应信号如图6所示,2种方法测点响应表现出类似的规律:即作为激励点的6号点,其响应速度幅值最大,1、3、7、8、10、13号测点响应速度幅值在0.05 mm/s左右,2、4、9、11、14号测点响应速度幅值在0.02 mm/s左右,5、12号测点响应速度基本小于0.02 mm/s。与跳跃激励时的能量传递方式类似。首先,作为激励位置的6号点,其振动为典型的屈伸运动信号,以此作为激励中心,能量传到其相邻的3、7、10号测点,而7号测点由于横梁增加了结构的阻尼,能量传递率下降,响应信号稍微小于3、10号测点;其次,在次相邻的1、8、13号测点速度幅值相对于相邻测点有所减小,同样由于传播路径上横梁吸能作用,8号测点的速度幅值相对于其他2个测点有所减小;再次,随着测点位置远离激励点位置,传递到2、4、9、11、14号测点的能量继续降低,幅值减小到0.02 mm/s左右;最后,距离激励中心最远的5、12号测点的响应速度最小。 图6 6号测点屈伸激励时14个测点速度响应Fig.6 The speed response of 14 points under the bounce excitation of No.6 point 在屈伸激励过程中,能量的传递总体上以激励点为中心向四周进行辐射,能量经过不同的路径传递后,响应速度会以振动中心为基准,能量的传递会因为路径上的梁柱作用出现局部减小的情况。有限元能量的传递需要通过各个单元节点进行数据传递,能量的传递规律是以激励点作为能量中心通过单元节点向四周传递,这与实验响应信号保持很好的一致性。在屈伸运动激励的实验测试中,其输入的能量受到周围结构的影响较大,因此响应信号规律性不强,有限元方法则表现为规律性较强的波动。 对比跳跃和屈伸运动作为激励的楼盖响应,可以看出,楼盖结构的14个测点变化规律基本一致,尤其是在有限元方法中,规律更加明显。这是由于对于同一研究对象,在2种运动激励下,楼盖的能量传递方式基本相同;然而,屈伸运动的响应速度幅值是跳跃运动响应速度幅值的1/10,这是由输入的能量大小决定的;跳跃运动激励下,所有测点的响应速度表现为拍振的响应,而屈伸运动激励下,由于振动能量在传播过程中对楼盖阻尼敏感,所有点的速度响应则表现为随机响应状态。 为了进一步对照2种方法的一致性,全面系统的分析楼盖结构整体动力学特性,分别对比试验和有限元计算,在2种激励形式下,不同时刻楼盖整体结构的速度响应云图如图7、8所示,分析2种激励形式下,楼盖系统的动力学响应规律。 图7 跳跃激励下楼盖速度响应Fig.7 Velocity response of floor under jump excitation 图8 屈伸激励下楼盖整体速度响应Fig.8 Velocity response of floor under bounce excitation 提取不同时刻下楼盖整体结构的典型速度响应云图,对比每个时刻下对应的各个点,在试验和有限元仿真的响应云图,可以看出,在2种激励下各自的响应幅值和振型,在对应区域的各个时间点的结果基本一致,有限元分析能够准确反映楼盖结构的振动形式和能量变化规律。 进一步对比4个不同时刻,在跳跃和屈伸运动激励下的速度响应情况可以看出,对于楼盖结构的速度激励,由于其具有周期性激励的形式,使得楼盖结构的速度响应以激励点为中心,向四周呈复合正弦波形传播,其波动随着时间呈周期性变化,整体结构随着时间的速度的峰值也呈周期性变化;对比跳跃和屈伸激励状态的速度响应可以看出,跳跃激励的速度响应值与屈伸激励响应值相差一个数量级,并且跳跃传播的能量波动范围大于屈伸激励能量范围,整体结构速度的响应更加连续具体的反映了楼盖结构在2种激励下的能量传递规律和振动规律。 位移的变化是反映楼盖结构在受到载荷作用下,楼盖保持稳定性的一个重要方面,通过有限元方法可以对各种激励作用下的楼盖位移变化进行分析,对楼盖结构的稳定性提供参考。 在跳跃激励作用下,楼盖结构各个监测点表现为周期性振动变化趋势(图9)。 图9 跳跃激励位移响应曲线Fig.9 Displacement response curves of jump excitation 同时各个测点从整体上看,有向不同的方向运动的趋势,由于跳跃激励能量比较大,位移响应主要以周期性振动形式变化,在重力和跳跃激励函数的共同作用下,使得位于不同位置测点上的位移,表现出不同的运动趋势,1、2、13、14号测点位移最大,这是由于测点在外侧横梁位置,跳跃激励的能量受到相邻立柱横梁的阻隔作用,主要受到自身重力的作用,并且在自身重力作用,测点位置有向下运动趋势;7、8、9测点与激励点在一根横梁位置,因此受到跳跃激励的影响相对明显,使得测点受到周期性激励的影响,成复合正弦波形变化;3、4、5、10、11、12测点位移较小,由于在4、11测点位于立柱支撑位置,限制了2点的运动,使得此处的测点位移最小。立柱位置和靠近激励点位置的测点位移向上微小运动,远离的测点向下运动,呈复合正弦波形变化。 在屈伸激励作用下,各个测点总体上与跳跃激励效果一致,有向不同的方向变化的趋势(图10),然而由于激励载荷较小,使得每个测点的周期性波动微小,在重力和屈伸激励的共同作用下,使得各个测点的位移表现出不同的规律。1、2、13、14号测点位移最大,这是由于在外侧位置主要受到自身重力作用,测点位移主要向重力方向变化;7、8、9测点受到屈伸激励的影响相对明显,使得测点受到振动激励的影响呈复合正弦波形变化;3、4、5、10、11、12测点位移较小,主要由于在4、11测点受到立柱的支撑作用,限制了其位移变化。立柱位置和靠近激励点位置的测点位移向下微小运动,远离的测点向上运动,呈复合正弦波形变化。 图10 屈伸激励位移响应曲线Fig.10 Displacement response curves of bounce excitation 对比在2种激励下楼盖局部测点的响应规律可以看出,相对于屈伸运动激励的变化,跳跃运动输入较多的能量,测点位移幅值表现出明显的周期性运动,而屈伸激励作用时,其位移幅值变化较小;从位移响应整体变化规律来看,2种激励形式的最终振动平衡位移相近,位移的变化是在重力作用的基础上产生的周期性变化。跳跃激励的振动幅值是屈伸激励振动幅值的10倍,跳跃激励对系统具有更直接的影响作用。在激励过程中,由于楼盖结构自身的特点,使得2种激励形式下的位移响应变化都出现周期性复合正弦波形传播。但传播过程中受到立柱横梁的影响,能量传播受到限制,在中间位置靠近激励点的测点受到激励运动的影响明显。 对楼盖整体结构有限元模型位移结果进行进一步分析可以看出,整体位移的变化反映了楼盖的变形规律。从位移变形规律来看(图11、12),跳跃、屈伸运动激励使楼盖结构在激励点附近出现向上运动趋势,位移出现最大值,从整体结构位移分布来看,2种激励产生的位移分布规律基本一致,即在立柱支撑位置的位移,明显高于无立柱支撑和梁顶位置。而由于跳跃激励相对屈伸激励具有更大的能量峰值,因此,对中间激励位置产生更明显的影响,跳跃激励位移峰值明显高于屈伸激励位移峰值。 图11 跳跃激励下楼盖整体位移响应Fig.11 Displacement response of floor under jump excitation 图12 屈伸激励下楼盖整体位移响应Fig.12 Displacement response of floor under bounce excitation 为了进一步研究楼盖结构在不同激励下的安全性,从2种激励下的楼盖应力的响应进行分析(图13、14),重力的作用和立柱的支撑影响,使得应力集中出现在立柱所在的2行横梁位置,横梁结构承受了最大的压力,成为危险位置,同时由于2种激励的扰动作用,使得激励地点附近横梁的应力集中值减小。跳跃激励的能量输入大于屈伸运动,使得激励对横梁的影响更加明显,对整个楼盖结构的振动位移产生较大的影响,对楼盖产生较大的危害。 图13 跳跃激励下楼盖整体应力响应Fig.13 Stress response of floor under jump excitation 图14 屈伸激励下楼盖整体应力响应Fig.14 Stress response of floor under bounce excitation 1)通过单点拾振获取所测楼板各测点的振动响应速度,通过傅里叶级数理论拟合得到了激励位置的速度激励函数,分析对比了2种激励下楼盖的实验和数值响应结果,表明速度激励函数结合有限元方法进行数值分析与实验值对照较好,证明了理论计算的可行性。 2)单人单点激励时,跳跃和屈伸作用到楼盖的能量传递规律相同;跳跃运动激励下,所有测点的响应速度表现为拍振响应,而屈伸运动激励下,所有点的速度响应则表现为随机响应状态,这是由于输入能量较低时,速度响应容易受到楼盖结构的扰动而出现无规律运动状态。 3)从振动位移角度,解释了人致振动下楼盖危险位置位于中间悬空位置,应采取有效的措施,加强中间位置的结构支承。 4)通过有限元方法分析可以看出,在2种激励的周期性作用下,楼盖结构会出现规律的复合正弦波运动形式,并使激励位置出现向上的运动趋势。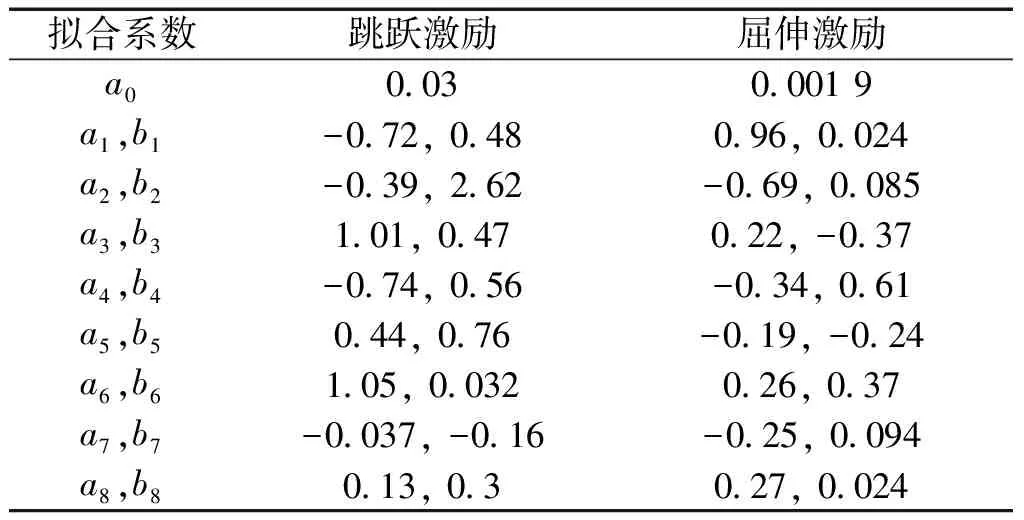

2.2 有限元模型

2.3 材料参数选取
3 人致振动激励瞬态分析
3.1 各测点速度对比分析



3.2 楼盖整体速度响应对比分析



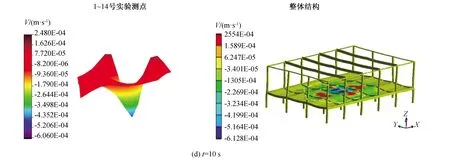
3.3 各测点和楼盖整体位移响应及应力分析

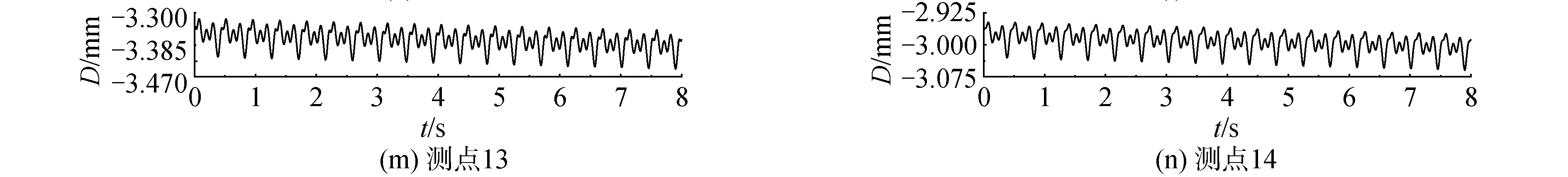


4 结论

