一种跳频信号的时频分析和参数估计方法
冯维婷,梁 青,汪一楠
(西安邮电大学 电子工程学院, 陕西 西安710121)
跳频通信信号的频率随时间按伪随机规律变化,具有不易截获、组网方式灵活和抗干扰能力强等优点,在军事和民用通信中得到了广泛应用[1-2]。在通信侦察和电子对抗等领域中,获得对方跳频通信信号的跳频频率、跳频周期和跳变时刻值等参数信息是破译及干扰其通信的首要条件[3]。估计跳频通信信号相关参数信息一直是信号处理领域研究的热点[4]。
跳频信号为非平稳信号。由于时频分析方法能够表征不同时间和频率的信号能量密度,成为目前跳频信号特征提取的主要方法。经典的时频分析方法包括短时傅里叶变换[5](Short Time Fourier Transform, STFT)、小波变换[6](Wavlet Transform, WT)和魏格纳-威尔[7-8](Wigner-Ville Distribution, WVD)。受限于Heisenberg原理或者存在非期望交叉项等原因,采用这些经典的时频分析方法时,存在时间和频率分辨率不能兼得或者分辨率较低等问题,从而影响了跳频信号非平稳特性的准确表示。
2011年,Daubechies等提出了同步压缩变换[9](Synchro-Squeezing Transform, SST)方法。该方法是一种高时频分辨率的时频分析方法,其以STFT或WT为基础计算信号的线性时频谱,对时频谱进行压缩,得到新的时频谱[10-11]。较之原时频谱,采用SST方法得到的新时频谱具有更高的时频分辨率。SST方法有着广阔的应用前景,然而该方法也存在不足之处,如具有较差的噪声鲁棒性[12]。为此,阮婉莹等[13]将变分模态分解引入SST,以提高SST的噪声鲁棒性。但是,该方法的推导过程基于瞬时频率为连续函数的信号的情况,对瞬时频率有跳跃点的跳频信号,在跳变时刻的时频分辨率明显较低。
针对SST方法分析跳频信号存在噪声鲁棒性较差和跳变时刻时频分辨率较低的问题,拟提出一种适合跳频信号时频分析的改进SST方法。根据跳频信号的特性重构瞬时频率,利用重构的瞬时频率对原时频谱进行压缩,以提高对跳频通信信号参数估计的精度。
1 信号模型与同步压缩变换
t时刻的跳频信号模型[14]可以表示为
s(t)=
(1)
其中:A表示信号的幅度;0≤t≤T,T表示信号的时间长度;fk表示第k(k=1,2,…,M)跳频频率;Th表示跳变周期,T0表示第一跳起跳时刻;j为虚数单位;rectTh(t)为单位门函数,其宽度为Tb。
t时刻混有噪声的接收信号可以表示为
r(t)=s(t)+w(t)
(2)
其中,w(t)为高斯复噪声,其均值为0,方差为σ2。
采用STFT作为SST方法的基础,将r(t)的STFT形式定义为
(3)
其中:f表示信号的频率;g(τ-t)表示随时间移动的窗函数,τ为窗长。RSTFT(t,f)表示接收信号STFT后在整个时间-频率轴上的二维分布。
假设第一跳起跳时刻为0,跳频频率为fk,持续时间为Th的第k跳跳频信号可以表示为
sk(t)=Aej2πfkt
(4)
式中,(k-1)Th 式(4)的傅里叶变换形式为 S(f)=Aδ(f-fk) (5) 式中,δ(f-fk)是在频率值fk处,强度为1的冲激函数。 式(5)表示在接收时间(k-1)Th 为了提高时频分辨率,可利用信号STFT的结果计算二维瞬时频率fI(t,f)的估计值。其计算表达式为[15] (6) 式中,∂tRSTFT(t,f)为RSTFT(t,f)对时刻t的一阶偏导。 (7) 在运用SST方法估计跳频信号的参数的过程中,信号瞬时频率的获取是算法的关键。只有获取高精度的瞬时频率估计值才能够得到能量高聚集的同步压缩结果。为此,提出一种改进的SST方法并进行参数估计。 式(6)计算瞬时频率估计值的表达式中有求导运算∂tRSTFT(t,f)。求导运算对噪声敏感,也对噪声背景下跳频信号的跳变部分敏感,容易带来较大的估计误差,从而导致对跳变部分的时频分析性能往往明显弱于连续部分。跳频信号的瞬时频率是分段连续的,存在跳变点,因此,式(6)并不适用于跳频信号的瞬时频率估计。基于以上考虑,结合跳频信号的特点,改进跳频信号的瞬时频率估计方法,将这种改进方法称为Hop-SST方法。对跳频信号瞬时频率估计采用如下思路。 对于原时频谱RSTFT(t,f),提取时刻t的所有时频系数峰值对应的频率,得到时刻t的时频脊线 (8) 在整个时频谱中,时频脊线fR(t)值为时刻t跳频信号能量聚集的频率点,高斯噪声能量均匀分布于整个时频谱不会聚集。因此,时频脊线就是跳频信号瞬时频率的一维估计值。基于fR(t)构造瞬时频率的二维估计值 (9) (10) 式中,N表示时间采样点数。 图1 无噪声时和x(f)的波形图 图2 SNR为-5 dB时和x(f)的波形图 (11) 图3 重构的波形图 利用Hop-SST时频分析方法得到跳频信号时频谱的过程,可以总结为如下具体步骤。 步骤1对接收信号进行STFT,得对应的时频谱RSTFT(t,f)。 相比于SST方法,Hop-SST时频分析方法改变了瞬时频率的估计方式,没有进行求导运算,增加了基于时频脊线提取的瞬时频率预估计及二值化、各跳频频率聚类,瞬时频率的修正等运算。增加的运算量主要为二维平面的一次峰值搜索、沿频率轴的一次累加和两次比较运算,与SST方法对比,增加的运算复杂度不高,适合实时信号的处理。 对于混有噪声的跳频信号,需要估计跳频频率、起跳时刻和跳频周期等3个参数。 信号的参数估计过程的原理为,首先,基于Hop-SST方法得到的时频谱,再提取时频脊线,并进行修正。修正后的时频脊线为常量分段信号。其次,对时频脊线进行差分运算。跳变时刻的差分值明显较大,而非跳变时刻差分值为0。根据这一特点,检测差分值的非0值时刻即可以检测出跳变时刻。两个相邻的跳变时刻之间的时频脊线对应的常量即为该段时间内的跳频频率估计值。最后,将接收时间T减去第一跳起跳时刻T0和最后一跳起跳时刻,对剩下的相邻跳变时刻值两两作差并取平均,从而得到跳变周期Th的估计值。具体有如下4个步骤。 步骤2进行fRIM(t)的差分运算,记录差分结果中非零值对应的时刻,即估计出跳变时刻。 步骤3取相邻两个跳变时刻的中点对应频率值,得到跳频频率的估计值。 步骤4剔除接收时间T的第一跳和最后一跳的跳变时刻,计算相邻两个跳变时刻之间的间隔并取平均得到跳变周期估计值。 仿真条件为,假设接收到的信号是经过下变频的含噪跳频信号,其采样频率fs为1 024 kHz,采样点数N为1 024点,时间长度T=1 ms。假设第一起跳时刻T0=0,跳频周期Th=0.125 ms,最小跳频频率值fmin=50 kHz,跳频频率间隔为50 kHz,共有8个跳频频率,最大跳频频率值fmax=400 kHz。选取的跳频序列为{50, 200, 100, 300, 150, 400, 350, 250},其单位为kHz。STFT中的窗函数采用旁瓣较低的汉宁窗,设定长度为155点。 在信噪比为10 dB时,分别采用STFT方法、SST方法和改进的Hop-SST方法得到的二维时频谱图如图4所示。 图4 SNR=10 dB时3种方法的二维频谱图 由图4(a)可见,接收信号经STFT的时频系数展开较宽,频率分辨率低。图4(b)SST方法的时频系数更加聚集,频率分辨率高,但在频率跳变时刻时频系数较分散。图4(c)Hop-SST方法改善了频率跳变时刻时频系数分散的现象。 在信噪比为-5 dB时,分别采用STFT方法、SST方法和改进的Hop-SST方法得到的二维时频谱图如图5所示。 由图5可见,在低信噪比条件下,图5(a)STFT方法和图5(b)SST方法的时频谱模糊不清,受背景噪声影响严重;图5(c)Hop-SST的时频谱清晰,且没有背景噪声,这是由于根据跳频信号特点重构瞬时频率的过程中不仅聚集了能量,而且抑制了噪声。 图5 SNR=-5 dB时3种方法的二维频谱图 采用瑞利熵定量评价时频分辨率的高低。瑞利熵值越小表示时频分辨率越高。不同信噪比情况下3种方法的瑞利熵对比结果如图6所示。 图6 不同信噪比情况下3种方法的瑞利熵 由图6可以看出,不同信噪比情况下Hop-SST方法的瑞利熵比STFT方法和SST方法的瑞利熵小,并且,低信噪比情况下Hop-SST的熵变化不大,说明该方法具有较强的抗干扰能力和更高的时频分辨率。 定义频率估计相对误差的平均值为 定义跳变时刻t估计相对误差的平均值为 定义跳频周期估计相对误差值为 设定信噪比SNR在5 dB~10 dB之间,以1 dB为间隔取值,分别采用STFT、SST和Hop-SST方法分别进行100次蒙特卡罗实验估计跳频频率、跳变时刻和周期。采用3种方法估计的跳频频率误差曲线如图7所示。分别采用STFT和Hop-SST方法得到的跳变时刻以及跳频周期的误差曲线分别如图8和图9所示。 图7 3种方法跳频频率估计的误差 图8 STFT和Hop-SST方法跳变时刻估计的误差 图9 STFT和Hop-SST方法跳频周期估计的误差 从图7(a)可以看出,不同信噪比条件下SST的频率误差比STFT的大,这是由于SST方法的噪声鲁棒性差,频率估计值受噪声影响大,SST方法虽然提高了时频分辨率但跳频频率估计值精度低。从图7(b)可见,在低信噪比条件下,Hop-SST的频率估计误差比STFT方法小,随着信噪比的提高,两者的频率误差值基本相等。这是因为Hop-SST中的频率聚类和迭代滤波能更好地消除噪声的影响,因此在低信噪比时跳频频率估计值精度更高。但是,随着信噪比的提高,噪声对频率估计结果影响减小,而Hop-SST是基于STFT的频率重排,故在高信噪比时两者具有相同的频率估计精度。 从图8可以看出,在低于-2 dB情况下,Hop-SST方法的跳变时刻误差小于STFT方法,但在-2 dB以后两条曲线基本重合,并且估计精度维持稳定,不再提高,这是由于两种方法中窗函数长度相等的缘故。跳变时刻估计值的精度受限于时频谱中窗函数的长度。根据傅里叶变换理论,窗函数时域上的长度和其频域上的带宽成反比。时域窗函数的长度越短,时间分辨率越高,但不可避免地,其频域的带宽就越宽,频率分辨率就越低,所以窗函数长度的选择是考虑综合时间分辨率和频率分辨率性能的折中结果。 图9的跳频周期估计误差曲线与图8类似,但其对跳频周期的估计是在跳变时刻估计基础上取平均得到的,误差有累计效应,故跳频周期的误差大于跳变时刻的误差。 综合图4~图9的跳频信号时频分析和参数估计仿真结果可见,本文Hop-SST方法的时频谱能量聚集度更高,参数估计精度在低信噪比下更高,抗干扰能力更强。 针对跳频信号的时频分析和参数估计问题,提出了改进的同步压缩变换方法。根据跳频信号的特点进行频率聚类和迭代滤波,改进了同步压缩变换中瞬时频率的估计方法,基于该方法得到跳频信号的时频谱图和参数估计值。仿真结果表明,Hop-SST方法较STFT方法和SST方法具有更清晰的时频谱,更有利于基于时频谱的跳频信号重构,同时,在低信噪比条件下具有更高的参数估计精度。
2 跳频信号的参数估计
2.1 改进的SST



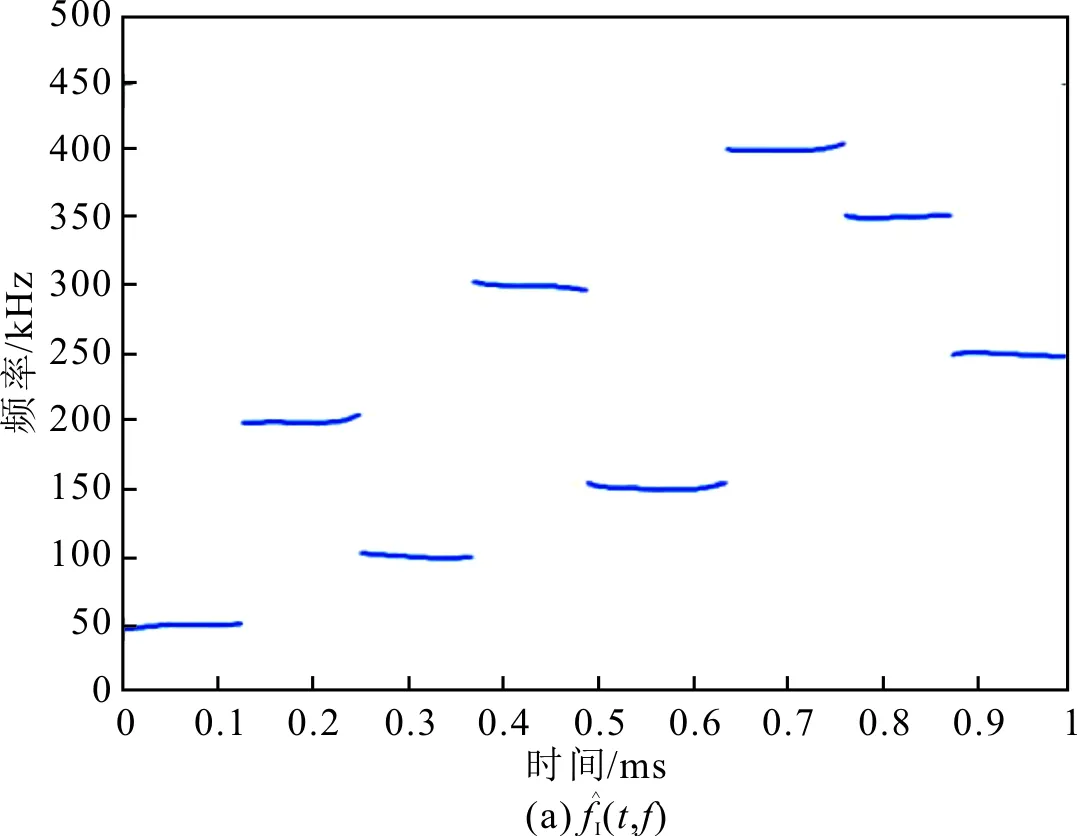









2.2 参数估计

3 仿真结果及分析
3.1 跳频信号的时频谱



3.2 跳频信号的参数估计






4 结语

