圆形直方图Otsu迭代阈值分割算法
王 东,杨贵峰,范九伦
(西安邮电大学 通信与信息工程学院,陕西 西安 710121)
图像分割[1-3]是指根据要求将图像细分为几个区域的过程,是图像处理到图像分析过程中的关键技术之一。最初的图像分割技术是通过将图像转换为灰度图像,然后对其利用各种分割算法进行分割处理,但单纯利用灰度图像信息往往无法提取出符合人们要求的目标。由于彩色图像比灰度图像提供了更为丰富的信息,因此,越来越多的学者开始将注意力转向彩色图像分割技术[4-7]。
从图像的分割原理上来看,灰度图像和彩色图像最主要的区别是在不同的空间维度对像素进行处理,灰度图像是基于一维亮度空间内,而彩色图像是基于三维颜色空间内。对彩色图像进行分割,既要选择合适的颜色空间,又要采用适合此颜色空间的分割算法。红绿蓝(Red Green Blue,RGB)颜色空间[8]将所有的颜色看作是由红(R)、绿(G)和蓝(B)等3种基本颜色混合而成,3个分量之间有着很强的相关性,因而不适合对这3个分量进行单独处理。通过对RGB颜色空间三基色的各种变换,可由RGB空间推导出其他颜色空间。其中,HSI(Hue Saturation Intensity)颜色空间就是由红、绿、蓝等3个通道对应的R、G和B值通过几何推导法公式转化为色调(Hue)、饱和度(Saturation)和亮度(Intensity)的HSI图像。
HSI颜色空间[9-10]与RGB颜色空间相比,色调、饱和度和亮度具有独立性,比较直观且符合人眼的视觉特性。利用色调(H)分量分割图像是一种重要的方法。Tseng等人[11]首次利用图像的色调(H)分量像素信息构造圆形直方图进行阈值化处理,通过对圆形直方图进行平滑滤波之后转化为传统的直方图,根据最大类间方差原理进行递归阈值化处理,其结果表明圆形直方图比传统直方图的分割结果更好。随后,Wu等人[12]将Otsu迭代算法用在圆形直方图上对血液细胞图像进行分割,并通过实验证明了该方法对血液细胞图像可有效分割。Dimov和Laskov[13]利用Otsu法将圆形直方图分成两类并对其进行扩展,分割图像为任意数量的类。Lai等人[14]提出了一种基于Otsu算法的高效圆形直方图阈值化的方法,当圆形直方图需要两个阈值进行二值化时,该方法能够在O(N)的时间内确定最佳阈值,其中,N为直方图的灰度级个数。Kang等人[15]提出了一种基于熵阈值的圆形直方图分割法,引入洛伦兹曲线分析圆形直方图,并将其转换为线性直方图,利用传统最大熵阈值分割法进行分割,分割效果较好。
在众多图像分割方法中,Otsu分割方法[16]因其简单、快速及性能稳定的特点已成为使用最为广泛的图像分割算法之一。在线性直方图上,利用穷举搜索法可简便求解Otsu法的最佳阈值,但穷举搜索法会带来巨大的计算量,而针对Otsu法的迭代算法则是改善此问题更直接有效的方法[1]。鉴于此,在前人对圆形直方图的研究基础上,提出两种圆形直方图Otsu迭代阈值分割算法,以期降低圆形直方图阈值分割算法的复杂度,提高分割效果。
1 研究基础
1.1 线性Otsu迭代算法
当图像像素的归类是以像素到各类中心的平方距离最小作为判决依据时,得到的阈值化方法称之为最大类间方差或最小类内方差法。因该方法是由日本学者Otsu[16]首先提出的,被称为Otsu法。
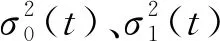
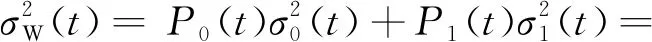
(1)
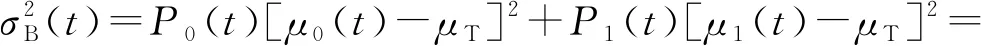
(2)
其中,μT为概率分布P的均值。
(3)
或
(4)
求解式(3)和式(4)的解一般做法是穷举搜索,针对穷举搜索法所带来的巨大计算量的不足,文献[18-19]提出基于梯度法的快速迭代算法,文献[20]采用图像灰度均值作为文献[18]迭代算法的初始值,将快速迭代搜索法的迭代次数降到最少。文献[1]描述的Otsu迭代算法是通过初始化阈值t(k),k=0开始,根据初始阈值t(k)计算两类相应的均值μ0(t(k))和μ1(t(k)),由μ0(t(k))和μ1(t(k))计算新的阈值,以此达到迭代的过程。具体的迭代步骤如下。
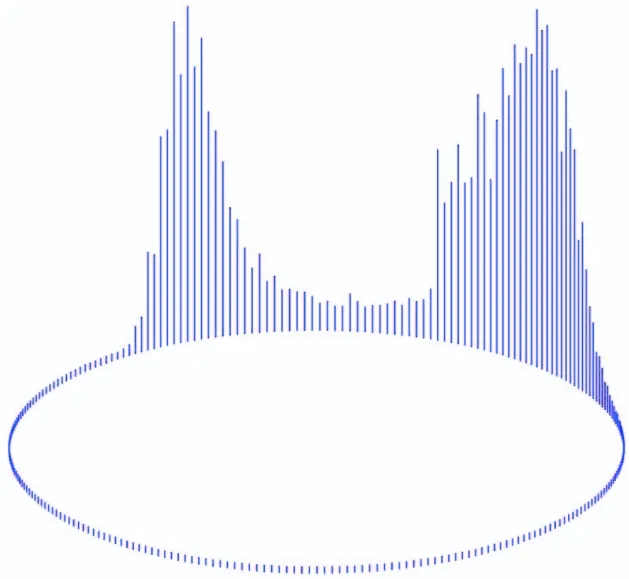
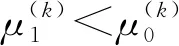
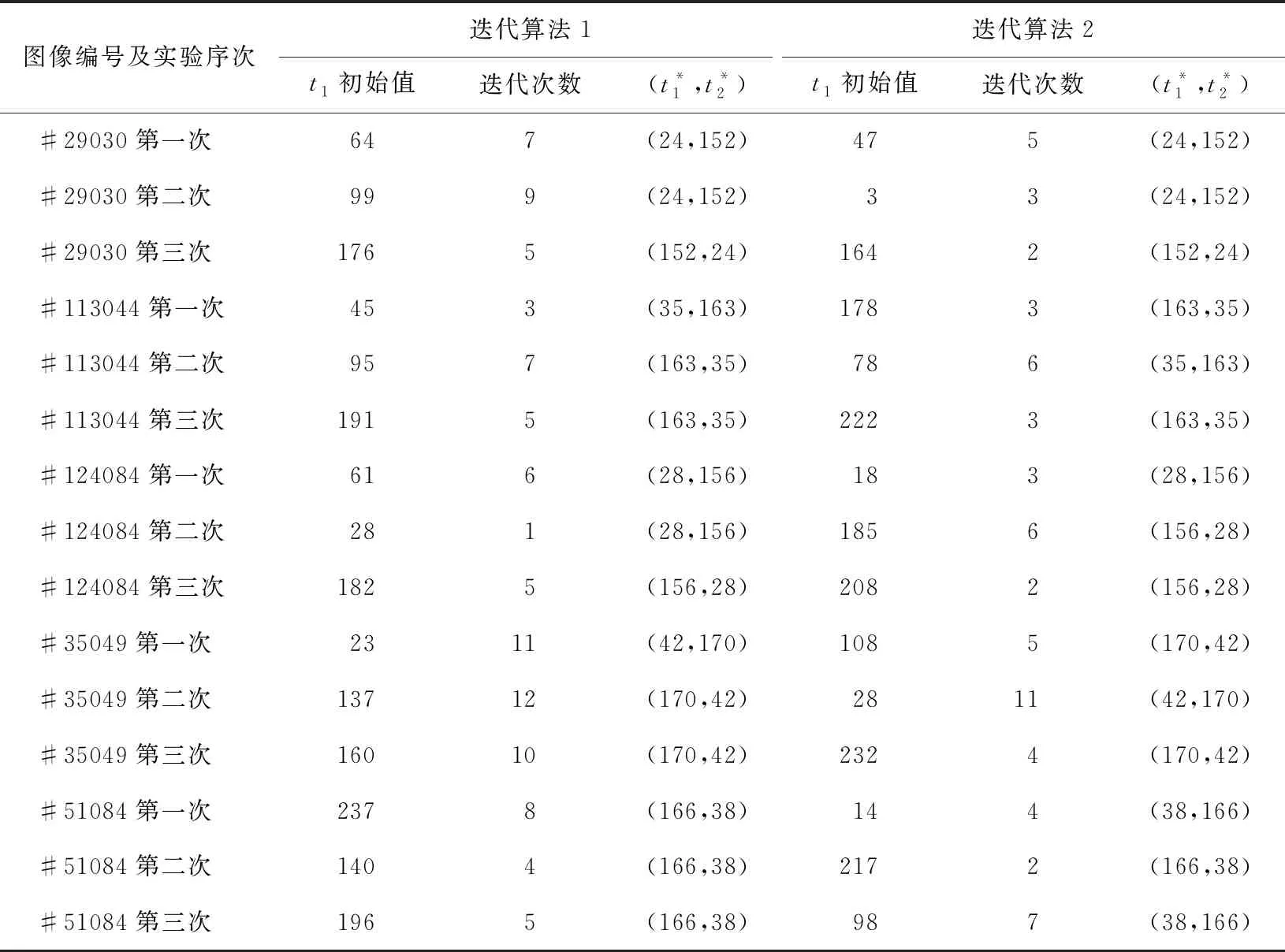
步骤1随机选取初始阈值0 步骤2根据t(k)计算μ0(t(k))和μ1(t(k)),即 (5) (6) 步骤3根据μ0(t(k))和μ1(t(k))计算 (7) 步骤4如果t(k+1)=t(k),停止迭代,否则令k=k+1回到步骤1。 在HSI颜色空间中,色调(H)分量是从[0°,359°]并以周期为360°呈周期性变化的,具有周期性和连续性,如图1所示。若采用传统线性直方图表示色调(H)分量的像素信息,将无法表达颜色的连续性和周期性。为了解决这一问题,把色调(H)分量的线性直方图的首尾横坐标相连形成一个圆,构造一个圆形直方图,如图2所示。与线性直方图阈值化不同的是,圆形直方图需要(t1,t2)两个阈值将直方图划分为两个部分,如图3所示。第一个阈值用于选择合适的起始点,第二个阈值用于把直方图分为t1,…,t2-1和t2,…,t1-1两部分。 图1 圆形色调平面图 图2 圆形直方图 图3 圆形直方图Otsu阈值化 假定圆形直方图被阈值(t1,t2)分成两类C0(t1,t2)和C1(t1,t2),则对应的先验概率P0(t1,t2)和P1(t1,t2)分别表示为 (8) (9) 需要特别注意,圆形直方图利用线性统计去标识时,其均值不能直接使用线性直方图上求解均值的类似表述。需要先将圆形直方图顺(逆)时针展开成线性直方图后,求解出相应的线性直方图均值,再逆(顺)时针旋转回去转化成圆上均值。 (10) (11) 由此得到圆上的两个对应均值分别表示为 (12) (13) (14) (15) 圆上总均值 显然, 圆形直方图上类内方差 (16) Wu等人[12]提出了另一种圆形直方图Otsu迭代阈值分割方法,具体算法步骤如下。 Wu等人提出的迭代算法经实验验证,在时间复杂度上并不具有明显的优势,且其迭代过程在有限步内不一定能够保证收敛。 考虑到在线性直方图上,Otsu迭代法是一种简便更直接求取最佳阈值的方法,故在Lai等人的研究基础上,提出两种圆形直方图Otsu迭代算法,进一步优化圆形直方图阈值化的时间复杂度。 (17) 由式(10)和式(11)可知 由此得到圆上的两个对应均值分别为 (18) (19) 基于上述分析,给出与Lai的搜索方式对应的迭代算法步骤如下。 (20) (21) (22) 迭代求解算法具体步骤如下。 (23) (24) (25) (26) (27) (28) 为了评估线性均值阈值化迭代算法(迭代算法1)和线性均值嵌套式迭代算法(迭代算法2)的有效性,主要进行两个部分实验。第一部分实验是针对图像的分割结果图以及图像的评价指标与Lai等人[14]提出的搜索方式和Wu等人[12]提出的迭代算法进行对比。第二部分实验是针对两种迭代算法在不同的初始值下,其最终得到的阈值点进行比较。 所有实验均在MATLAB 9.3.0(R2017b)上进行测试。测试图像均来自于Berkeley图库,图4为测试图像在RGB颜色空间上的彩色原图。由于圆形直方图是基于HSI颜色空间的,故给出了各彩色图像在HSI颜色空间中的原图,如图5所示。 图4 测试图像在RGB空间显示 对HSI颜色空间中的每个图像分别提取色调(H)分量,绘制的圆形直方图如图6所示,图中所有子图分别与图5中的子图对应。 图5 测试图像在HSI空间显示 图6 各测试图像的圆形直方图 分别利用Lai等人的搜索方式、Wu等人的迭代算法、迭代算法1和迭代算法2等4种算法对5个测试图像进行分割,结果如图7所示。 图7 不同算法的分割结果 为了进一步客观评估两种迭代算法的有效性,表1列出了4种算法的30幅图像平均像素精确度(Pixel Accuracy,PA)、Dice系数[21](Dice Ratio,DR)以及一致性系数[22-23](Conformity Coefficien,CC),其中,Dice系数值域为[0,1],是一种集合相似度度量函数,数值越大,相似度越大。 表1 不同算法的评价指标对比 从表1中的分割评价指标数据可以看出,两种迭代算法的分割结果均于Lai等人提出算法的分割结果一致,且分割效果均优于Wu等人提出的迭代算法。对于图4中#29030、#113044和#124084图像,Wu的算法并不能分割出完整的目标。图8是30幅测试图像使用不同分割算法的平均运行时间。从图8中可以看出,两种迭代算法的运行时间均明显优于Lai等人提出的搜索方式,迭代算法1的运行效率比Lai等人的算法提高了64%左右,与Wu等人的算法相比,时间缩短了4倍多。由于迭代算法2是嵌套式迭代,故其平均运行时间略高于迭代算法1,但与Lai等人的算法相比,仍要快接近于2倍,与Wu等人的算法相比,运行速度快3倍多。 图8 不同分割方法分割图像的平均速度 表2 各测试图像3次实验得到的阈值比较 从表2的实验数据可以看出,虽然两种迭代算法的初始值是随机选取的,但是每次迭代停止后得到的两个阈值并不会改变,即最终得到的阈值不会受到初始值的随机选取的影响。其次,迭代算法1和迭代算法2虽然迭代过程不同,但最终的迭代结果却是相同的。 针对圆形直方图Otsu阈值分割问题,考虑到在线性直方图上,Otsu迭代算法是一种简便直接的方法,提出了圆形直方图上的线性均值阈值化迭代算法和线性均值嵌套式迭代算法。实验验证结果表明,所提的两种迭代算法在有效提取目标的同时降低了时间复杂度。所提迭代算法是将圆形直方图Otsu迭代算法分为两类的情况,如何在多类的情况下降低时间复杂度,将有待于进一步研究。
1.2 圆形直方图



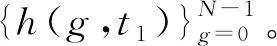
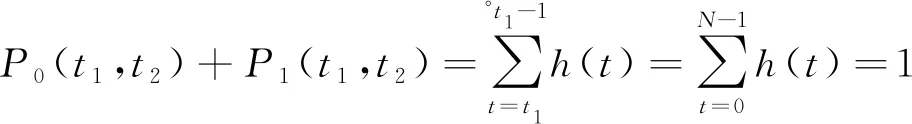
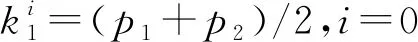
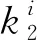

2 线均值阈值化迭代算法

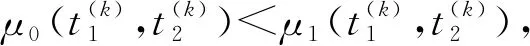
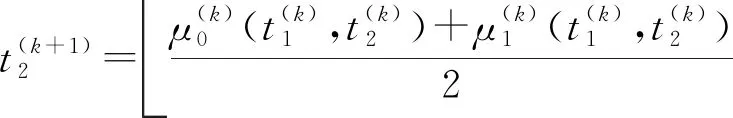

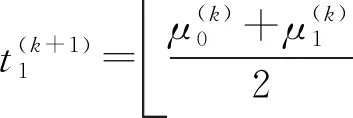
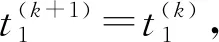
3 线性均值嵌套式迭代算法

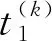


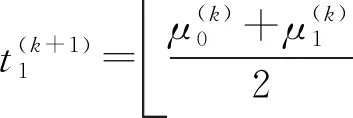
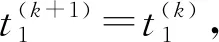
4 实验结果与分析






5 结语

