离子液体推力器性能影响因素仿真研究

范益朋，夏广庆*，鹿 畅，孙 斌，丁 亮

（1. 大连理工大学 工业装备结构分析国家重点实验室； 2. 大连理工大学 辽宁省空天飞行器前沿技术重点实验室：大连 116024； 3. 北京卫星环境工程研究所，北京 100094）

0 引言

离子液体推力器（ionic liquid thruster, ILT）是在微小卫星的需求下迅速发展的一种新型微牛级微电推力器，其利用静电喷射原理，具有结构精简、体积小、重量轻、功率低、推力精度高等特点[1]，可用作微纳卫星的动力系统，或作为分布式推力器应用于大型航天器[2]。作为推进剂的离子液体在室温下通常呈液态，且表面张力较小，电导率较高，故发射时无需为推进剂离解提供辅助部件；同时，离子液体黏度较高，能提供较大的流阻，适用于毛细作用被动式供给，无须压力供给系统；此外，离子液体可交替发射阴、阳离子，实现电荷自中和，无须配置中和器[3-4]。因此，离子液体推力器的应用前景极为广泛。

目前关于离子液体推力器的仿真研究主要是针对从离子液体中发射离子的过程，即关于泰勒锥形成过程与泰勒锥破碎发射离子的过程。例如：Borner 等利用分子动力学（molecular dynamics,MD）仿真模拟了不同电场强度和推进剂质量流量下发射电流的大小以及各种离子所占比例[5-6]；程世豪通过COMSOL 仿真软件研究了发射极阵列密度、电极间距、发射极内径对离子发射所需阈值电压的影响[7]；Kim 将有限元法（FEM）与有限差分法（FDM）结合到MD 仿真中，分析了引出极孔径、发射电压、发射极温度和润湿性等因素对发射电流大小、电流密度和离子速度的影响[8]。但截至目前关于离子液体推力器的研究并未涉及推力器结构对整体性能影响的多工况粒子网格（particle in cell, PIC）仿真分析。

本文着重研究离子液体推力器发射阵列几何结构参数对推力器性能的影响：首先基于PIC 法建立单个发射极的二维仿真模型；而后分析电极间距与引出极孔径改变引起的推力器推力和角向效率变化规律，以期为离子液体推力器的优化设计提供参考。

1 仿真模型

1.1 ILT 工作原理

离子液体推力器主要由发射极、引出极和推进剂储箱等组成，单个发射极结构如图1 所示。其基于静电喷射原理，通过在发射极和引出极间施加发射电压，使发射极尖端产生强电场，发射极尖端的离子液体受静电场力和表面张力的共同作用变形成泰勒锥[9]（Taylor cone），随后泰勒锥尖端破碎喷射出带电液滴以及溶剂化和未溶剂化的离子，并在电场中加速喷出。部分推力器在引出极后增添了加速极，实现对引出离子的进一步加速，以提高推力器推力和比冲[10]。

由于单个发射极产生的推力非常低，通常在十几nN 量级，难以满足实际应用需求，因此需要将发射极阵列化，以获得较大的发射电流和推力[11]。

1.2 仿真模型建立

阵列化后的发射极有多种类型：按阵列形式可分为一维阵列式和二维阵列式；按推进剂供给形式可分为毛细管型、外部浸润型和多孔基质型。其中，毛细管型发射极泰勒锥形成位置和离子发射位置相较于其他两种类型发射极更容易确定，且较为稳定，适合通过仿真探索一些规律性问题。离子液体推力器常见的工作模式是锥-喷流（cone-jet）模式，在此模式下，泰勒锥的母线可能是直线也可能是曲线[12]，并且随着使用液体的电导率的减小，喷流的区域逐渐向圆锥底部延伸[7]。因本文主要针对推力器宏观性能进行研究，故此处考虑母线为直线形式的标准泰勒锥模型，对单个毛细管型发射极建立了二维轴对称模型，如图2 所示，具体结构参数及工况如表1 所示。

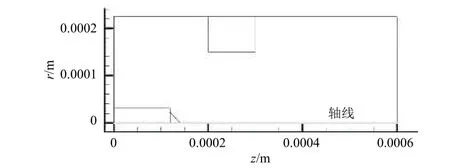
图2 单个毛细管发射极的仿真模型Fig. 2 Simulation model of a single capillary emitter

考虑工作在阳极工况下的发射极模型，其发射电压设置为3 kV，采用1-乙基-3-甲基咪唑四氟硼酸盐（1-ethyl-3-methylimidazolium tetrafluoroborate,EMI-BF4）作为推进工质。发射极工作在纯离子模式（purely ionic regime, PIR）下，即发射物中只包含单体（EMI+）、二聚体（[EMI-BF4]EMI+）、三聚体（[EMI-BF4]2EMI+）三种离子。离子总发射电流320 nA，各种离子所占比例取于Romero-Sanz 的实验结果[13]，如表2 所示。

表2 各种离子所占电流组分Table 2 Proportions of various ions in the current

上述模型基于PIC 方法建立。PIC 方法作为一种计算机数值模拟方法，通过追踪单个粒子的运动，对单个微观粒子的运动情况进行数值描述，再对组成物体的大量微观粒子进行统计平均，由此可得到宏观物体的物质特性和运动规律，可用于推力器性能研究。

如图3 所示，PIC 方法需要通过网格划分的方式将力场（一般为电场、磁场）离散化，同时将时间变量离散为一个个时间步长，分析粒子在当前时刻所受离散化力场的作用力，便可求得下一个时间步粒子位置与速度；进而再与外力场耦合，解算出新的力场；以此循环，直至系统达到稳态。

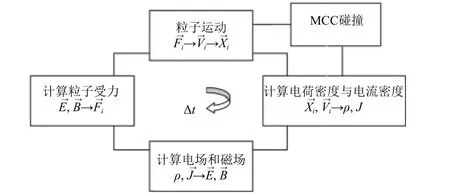
图3 PIC 方法流程图Fig. 3 Flow chart of PIC method

其耦合过程的核心思想是将网格内粒子的电量、粒子运动产生的电流等参数按一定的权重（如面积权重法、体积权重法等）分配至网格节点上，再计算网格节点上的力场参数[14]。

由于离子液体推力器为静电式电推力器，发射场中只包含静电场，故在PIC 算法中求解电场时不必求解完整的Maxwell 方程组，只需求解Poisson方程[15]

式中E为电场矢量。

仿真模型中，除发射极与引出极外，其余边界条件均设置为第二类边界条件（诺依曼边界条件），即

对于带电粒子在静电场中的运动，一般可描述为

式中：m为带电粒子质量；v表示粒子速度矢量；q为粒子所带电量；dt为时间步长。

最后，将上述各式离散化[16]，以获得各网格节点上的数值，并基于网格节点进行PIC 仿真计算。

由于离子发射所需电场强度的阈值约在109V/m量级[9]，电势在发射极与引出极之间的变化梯度极大，因此为保证仿真结果的准确性，兼顾到仿真时长，将该模型网格大小控制在1×10-6m。

1.3 推力器性能计算方法

本文主要研究内容为电极间距与引出极孔径改变引起的推力器性能变化，即以初始模型为基础，分别改变模型电极间距和引出极孔径，通过仿真，获得二者改变引起的推力器推力及角向效率变化曲线。

推力器推力T为[17]

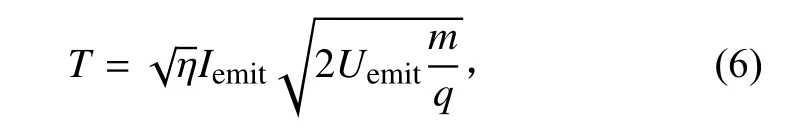
式中：η为推力器总效率；Iemit为发射电流；Uemit为发射电压；q/m为羽流中包含粒子的平均荷质比。

而仿真时，离子液体推力器推力能够通过对所有粒子的速度和质量进行统计获得，即

式中：n为通过推力统计截面的离子数量；mi为第i个离子的质量；viz表示第i个离子沿轴向的速度。

推力器角向效率ηangle为羽流轴向动能Ekz与总动能Ek之比，即

其中，Ekz和Ek可分别表示为：

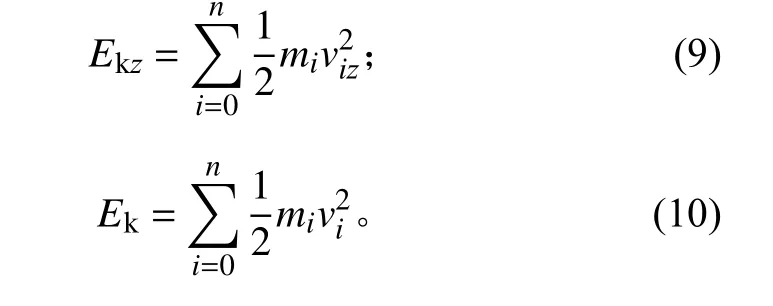
此外，还可通过编写仿真程序获得推进剂质量流量，进而计算出推力器比冲。推进剂质量为

再根据式(7)和式(11)即可计算出推力器比冲

式中g为重力加速度，取9.8 kg/(m·s-2)。

收集电流Ico计算方法与质量流量计算方法类似，可得

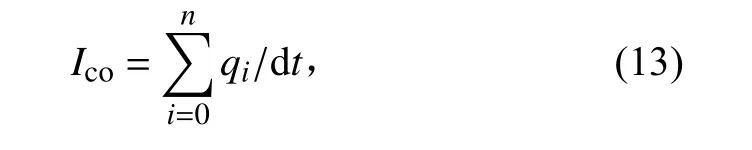
式中qi为第i个离子所带电量。

2 结果与讨论

2.1 初始仿真结果

在PIC 仿真达到稳态后对结果进行输出，可获得离子数密度分布、离子速度分布图像，以及推力、比冲曲线等。

图4 为稳态后的羽流离子数密度分布图像。图中羽流整体形貌呈圆锥状发散，具有一定的束流散射半角。在发射极尖端附近离子数密度最大，达1019/m3量级；经电场加速后离子扩散到引出极右侧的较大区域，此时轴线附近离子数密度降至1015/m3量级，且数密度从轴线沿径向向外呈现先减后增再减的趋势，羽流边缘处离子数密度仅达1014/m3量级。图5 为组成羽流的三种离子的数密度分布图。可见：虽然由于各种离子的质量及发射数量不同，三种离子数密度分布存在一定差异，但离子整体分布规律不变，即：离子数密度在发射极尖端位置最高，其次在靠近轴线附近相对较高，整体分布呈沿径向从轴线向外先减后增再减的规律。

图4 离子数密度分布Fig. 4 Distributions of ion number density

图5 三种离子数密度分布Fig. 5 Distributions of ion number density of EMI+, [EMI-BF4]EMI+ and [EMI-BF4]2EMI+

图6 为电场强度分布图。从图中可以看出：引出极左侧的电场强度整体上比引出极右侧高很多，在发射极尖端及引出极左侧尖端，电场强度更是比其他区域大了几个数量级。这表明离子能在通过引出极前即能够将势能转化为动能，实现较为完全的加速。如图7 所示，离子在通过引出极前整体平均速度已加速至约40 000 m/s；而电场矢量主要从发射极指向引出极，离子在电场中加速后，除了获得轴向的速度外，还将获得径向的速度。

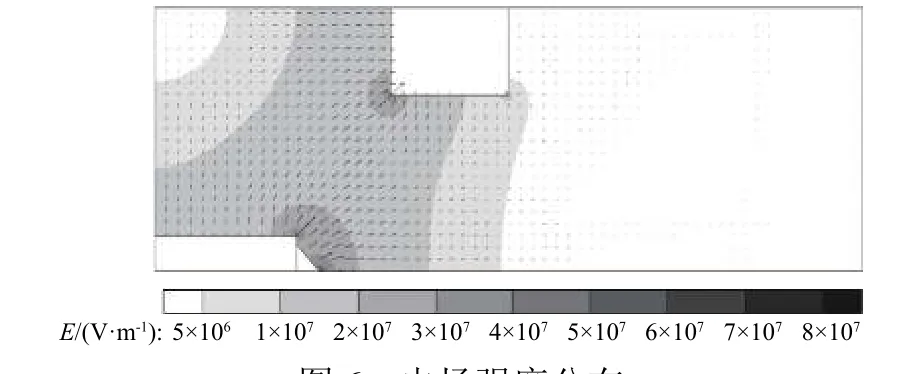
图6 电场强度分布Fig. 6 Electric field intensity distributions

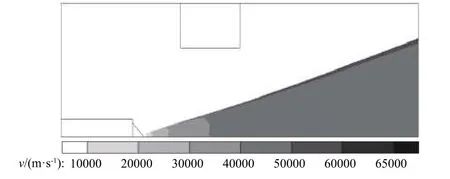
图7 离子速度分布Fig. 7 Ion velocity distributions

整体而言，离子在电场中加速后获得的速度以轴向速度为主，如图8 所示，其平均轴向速度可达约45 000 m/s；相比于轴向速度，径向速度最高仅约22 000 m/s。从图9 的电场强度分布图可以看出，轴向电场强度整体大于径向电场强度，因此离子在电场中加速后能获得高于径向速度的轴向速度。而羽流边缘附近的离子受电场加速后，其轴向速度虽低于羽流内部区域的离子速度，但径向速度比羽流内部区域离子的要高，因此羽流边缘离子的总速度相较于轴线附近的离子速度更高。

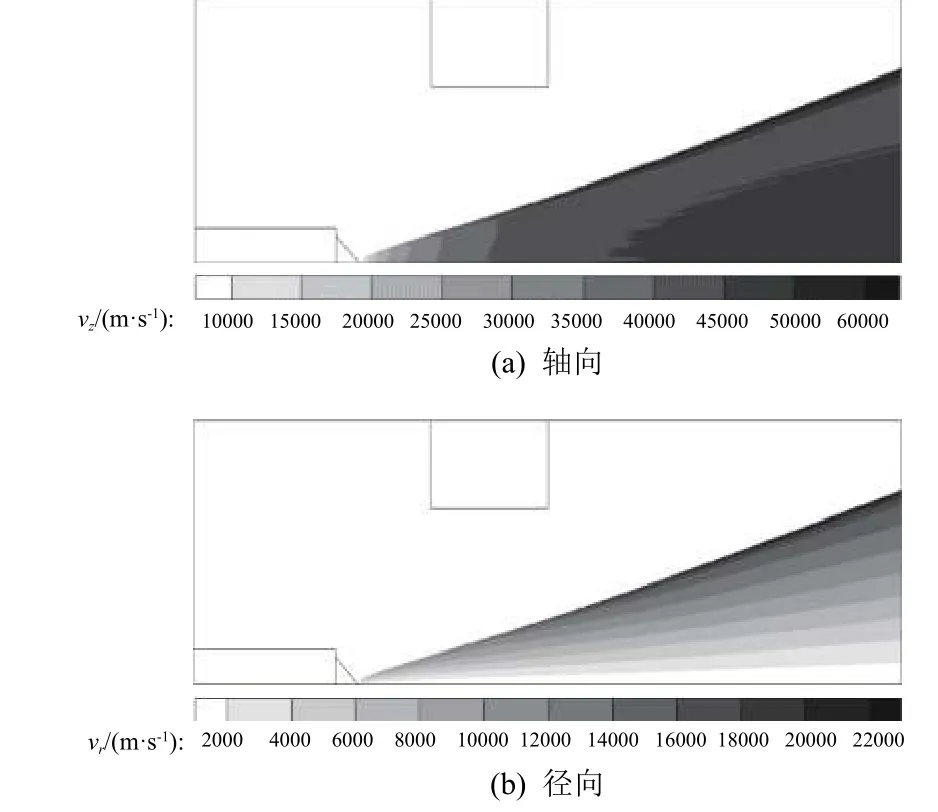
图8 离子轴向和径向速度分布Fig. 8 Ion velocity distributions in axial and radial directions

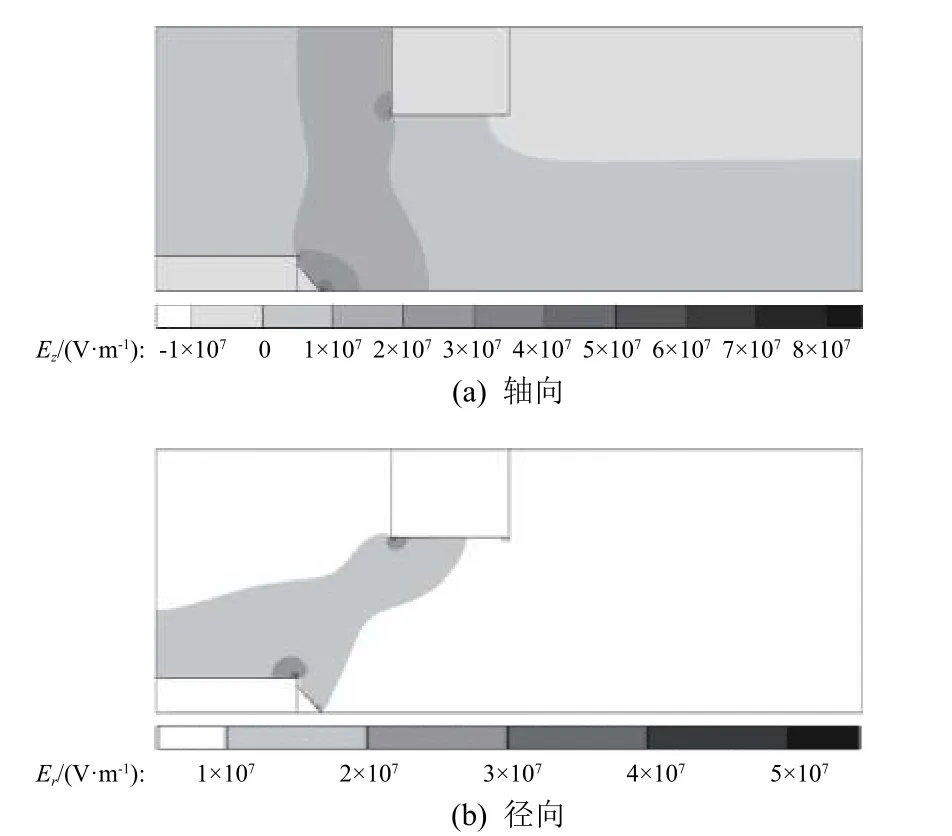
图9 电场强度的轴向和径向分布Fig. 9 Electric field intensity distributions in axial and radial directions

另外由于三种离子比荷不同，其在电场中的加速效应也不一样（如图10 所示），到达推力统计截面的时间会有差异。由图可见：单体离子比荷最高，在电场中加速后速度也最大，可达约60 000 m/s，能够最早到达推力统计截面；其次是二聚体，电场能将其加速至35 000 m/s 以上；最后是三聚体，受电场加速后速度约在30 000 m/s，最晚到达推力统计截面。故推力曲线呈现图11 所示的明显的阶梯状上升现象。

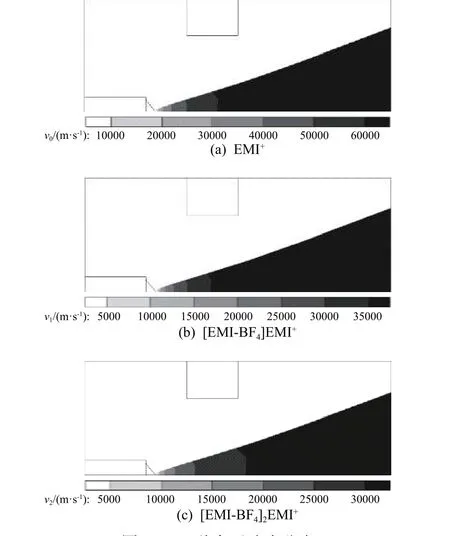
图10 三种离子速度分布Fig. 10 Ion velocity distributions of EMI+, [EMI-BF4]EMI+and [EMI-BF4]2EMI+

图11 推力和比冲曲线Fig. 11 Curve of thrust and specific impulse

而离子液体推力器被证明在发射极阵列化后，其单个发射极的工作状况几乎不受影响，因此可近乎成比例地提升推力[18]。如图11 所示，单个发射极的推力约为34 nN，考虑在1 cm2内集成480 个发射极，则其推力可达约16 μN/cm2，比冲保持在约4100 s。

2.2 电极间距影响

在初始模型基础上，保持其他参数不变，将电极间距由80 μm 逐渐增加至300 μm，获得平均推力及角向效率随电极间距变化曲线，如图12 所示。可见：在电极间距增加初期，推力增幅相对较大；随着电极间距的增大，推力增幅减小；在电极间距约280 μm 时推力达到最大值，约34.7 nN，随后出现减小的趋势；而角向效率随电极间距单调增加。

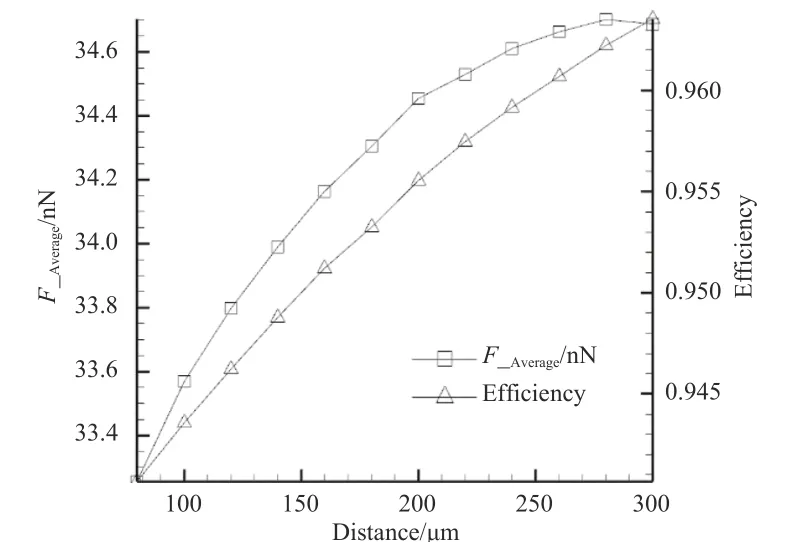
图12 平均推力及角向效率随电极间距变化曲线Fig. 12 Variations of average thrust and angular efficiency against the electrode spacing

在确保未出现羽流被引出栅极拦截的情况下，对该现象产生的原因进行了分析，如图13 所示。由于电场矢量主要由发射极指向引出极，在增加电极间距后，整体上电场矢量与轴线的夹角减小，即离子通过电场加速后轴向速度占总速度的比例增加，羽流的准直性有所提升，因此角向效率随电极间距的增加而不断增大；但电极间距的增加同样会导致电场强度减小，这将导致离子加速后的速度不断减小，因此随着电极间距的不断增加，离子经电场加速后获得沿轴向的动能所占比例不断增加，但离子总动能逐渐减小，在这两种因素的耦合作用下，离子轴向速度先增加后减小，在280 μm 时获得最大平均轴向速度，反映在推力上即为推力出现先增加后减小的趋势，在280 μm 时获得最大推力。

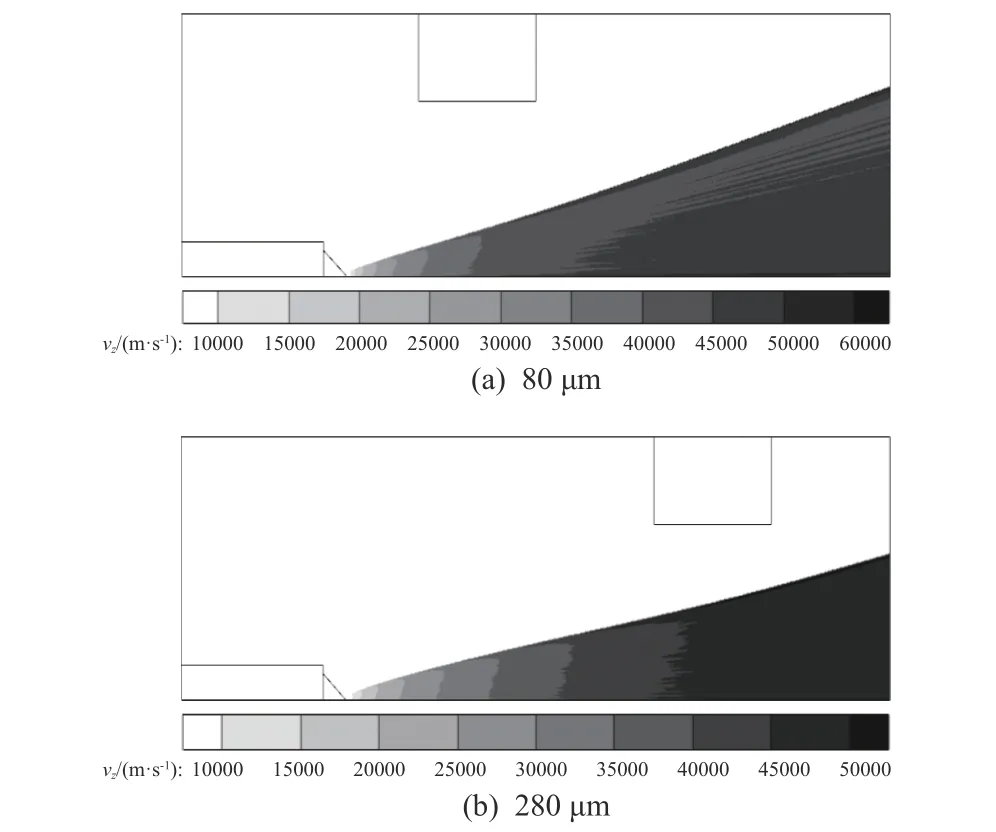
图13 不同电极间距的离子轴向速度Fig. 13 Axial velocity of ions with different electrode spacing

2.3 引出极孔径影响

通过改变初始模型引出极孔径，获得平均推力及角向效率随引出极孔径的变化曲线，如图14所示。

图14 平均推力及角向效率随引出极孔径变化曲线Fig. 14 Variations of average thrust and angular efficiency against the extractor aperture

随着引出极孔径由初始模型的300 μm 逐渐减小至80 μm，推力器推力逐渐增加，而角向效率却不断下降；当引出极孔径＜120 μm 时，推力曲线与角向效率曲线出现骤变。这是由于引出极孔径减小至120 μm 以下时出现了大量离子被引出栅极拦截的情况，造成明显的推力损失与栅极侵蚀，严重影响推力器寿命，故应尽量避免出现该情况。

研究离子未被引出栅极拦截时引出极孔径变化对平均推力和角向效率的影响，结果如图15 和图16 所示。在此情况下，引出极孔径的减小使得电场强度显著增加，从而使离子在电场中加速后获得的轴向动能与径向动能均有提升，而其径向速度增幅相较于轴向速度更为显著，即离子轴向动能占总动能的比例随引出极孔径的减小而逐渐减小。因此，在出现羽流被栅极拦截的情况之前，其角向效率随引出极孔径的减小而逐渐减小；而轴向动能占比虽然随引出极孔径的减小不断减小，但总动能不断增加，且增幅显著，故推力整体上呈现随引出极孔径的减小而不断增加的趋势。

图15 不同引出极孔径的离子轴向速度Fig. 15 Axial velocity of ions with different extractor apertures

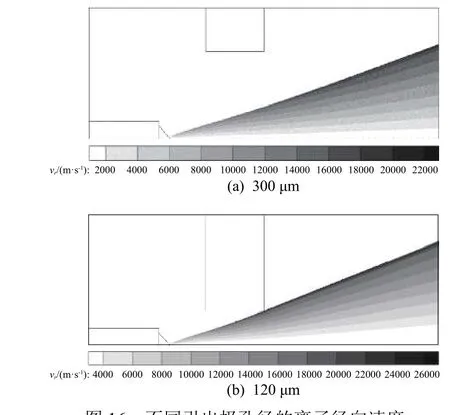
图16 不同引出极孔径的离子径向速度Fig. 16 Radial velocity of ions with different extractorapertures

3 结论

本文基于PIC 方法建立了离子液体推力器单个毛细管型发射极的仿真模型，获得了单个发射极的束流分布特性和性能参数曲线，随后着重研究了电极间距和引出极孔径对推力器推力和角向效率的影响，获得了发射极平均推力和角向效率随电极间距及引出极孔径的变化规律。仿真结果表明：

1）推力器角向效率与电极间距成正比，推力则受电场强度和电场方向的共同影响，随电极间距的增加先增大后减小；

2）在出现离子被引出栅极拦截的情况前，推力器角向效率与引出极孔径成正比，推力与引出极孔径成反比，但过小的引出极孔径会造成栅极侵蚀，严重影响推力器性能和寿命；

3）在上百个发射极实现阵列化之后，发射场几何结构的改变引起的推力变化预计达μN 量级。

由于本研究未考虑电场变化引起发射离子数量的变化和不同种类离子所占比例的变化，因此推力曲线与实验存在一定差异，但推力器角向效率变化规律不受发射离子数量和比例影响。在后续研究中将考虑电场变化引起发射离子数量和比例的变化，耦合多种影响推力器性能的因素，使仿真结果更贴合实际。