空间相机地面装调重力卸载仿真优化方法

白 杰，孙熠璇，刘子嘉，杜建祥

（北京空间机电研究所，北京 100094）

0 引言

空间相机在轨工作时处于微重力（10-3g～10-4g）环境，而其装配与测试一般在地面重力环境下进行，因此需要进行重力卸载来模拟空间微重力环境[1]，以保证成像光路中所有光学元件的面形、位移及角度在地面测试过程中与在轨成像时一致。空间相机对光学元件的面形及位置精度有极高的要求，特别是具备可见光成像功能的空间飞行器，其反射镜的面形RMS 一般需要达到(1/50)λ，甚至(1/60)λ；反射镜的位置精度一般需要达到0.01 mm 级别，甚至μm 级别。同时，受火箭发射能力及发射成本的制约，常常要求空间相机的光机主体进行结构轻量化设计，因此空间相机常具有尺寸大、刚度低的特点，且其光机系统对位置稳定性要求很高，使得空间相机地面装调过程中的微重力环境模拟异常复杂困难。在空间相机地面装调重力卸载仿真计算过程中，仿真模型较结构实际状态存在误差，故一般要求仿真计算的反射镜面形RMS 及位置精度优于指标要求的30%，因而对于一般的反射镜，仿真计算结果需满足其面形RMS 优于(6/1000)λ，位置变化量小于1 μm。

针对空间相机及其他空间飞行器的地面微重力环境模拟，诸多学者设计了不同的重力补偿方案和重力卸载结构[2-6]，但未发现有文献提出有效的重力卸载点选取及卸载力计算方法。然而，随着超轻量化空间遥感相机、2～4 m 大口径及4～10 m 超大口径空间遥感相机的研制逐渐成为国内外光学遥感领域的研究热点[7]，在空间相机光机结构装调过程中，有效重力卸载点的识别难度增大，需设置的重力卸载点个数增多，利用一般的试错法调整卸载点位置及卸载力已无法满足要求，而其仿真优化的难度亦随着相机口径的增大和结构轻量化水平的提高呈指数级增加。

鉴于此，着眼于高效、快速地获得使系统优化目标精度最佳的卸载点系及最优卸载力，本文提出一种基于贪心算法结合天牛须搜索的重力卸载仿真优化方法。贪心算法的策略为将单个全局最优问题划分为若干个迭代的局部最优子问题，通过求解一系列的局部最优解来获得全局最优解[8-9]。基于此策略，可将光机系统重力卸载的仿真优化问题分解为逐个提取系统的相对最佳卸载点，从而获得系统的相对最优卸载点系，继而计算出其对应的最优卸载力。每组卸载点系的最佳卸载力值利用天牛须算法进行迭代搜索计算。

1 重力卸载仿真优化方法

1.1 光机系统建模

将空间相机的光机系统结构离散化，建立结构刚度矩阵K；设离散化光机系统结构节点的位移矢量为d，所受到的力为F，则可建立空间相机光机系统的结构方程

求解式(1)即可获得光机系统各个离散位置的变形量。

在利用基于贪心算法结合天牛须搜索的光机系统重力卸载仿真优化过程中，每组卸载点系的最佳卸载力采用天牛须搜索算法进行迭代计算，无须知道系统具体的结构求解模型，只需在每次计算求解式(1)前设置力矢量F，并能获取式(1)求解后的位移矢量d即可。因此，可以建立光机系统的有限元模型，并利用有限元软件的二次开发功能实现对力矢量F的设置和对位移矢量d的获取。

光机系统的基本建模过程如下：

1）利用有限元软件建立光机结构的离散化网格模型；

2）利用有限元软件建立光机结构的位移边界条件及初始力边界条件，前者为光机结构装调时的固定约束，后者为地面重力加速度；

3）利用有限元软件建立光机结构系统的静力学分析工况；

4）利用有限元软件的二次开发功能建立优化算法与有限元软件的通信接口，进行数据交换与相关设置。

将优化算法调整光机系统力矢量F，以及控制有限元软件分析计算获得最终系统位移矢量d的过程用f1表示，则有

1.2 贪心算法

在空间相机的地面装调重力卸载仿真优化过程中，若采用传统的牛顿法或梯度下降法，则需要建立光机系统的精确求解方程，并推导计算目标值的方向导数或最快下降梯度。而光机结构系统离散化后的节点数量非常庞大，一般在几万甚至几十万个以上，相应地，系统方程的维度也在几万甚至几十万个以上，其方程的建立、求解和推导异常复杂，并且针对不同的优化目标所建立的方程会有差异，需重新进行推导和计算；若利用一般的试错法进行计算，随着光机结构系统复杂程度的增加，需施加卸载力的个数也将不断增多，计算量会呈指数级增加，导致优化效率急剧降低。而贪心算法的基本策略优势则可以将复杂问题分解简单化，且在求解子问题的过程中，可利用天牛须搜索算法进行迭代搜索计算，无须建立光机系统的具体求解方程，因而对不同的优化目标具有更好的适应性，能更加高效地获得系统最优卸载力。

基于贪心算法的基本策略，将光机系统重力卸载的仿真优化分解为逐个提取系统最优卸载点的迭代过程，具体如下：

1）提取光机结构的可行卸载点集。

2）第1 次计算时，从可行卸载点集中提取1 个或1 组最佳卸载点；利用天牛须搜索算法计算被选卸载点的最优卸载力，以使系统获得最佳性能。

3）第i(i＞1)次计算时，从可行卸载点集中提取1 个或1 组最佳卸载点，该个或该组卸载点与前(i-1)次添加的卸载点共同组成卸载点系；利用天牛须搜索算法计算每组卸载点系的最佳卸载力，以使系统获得最佳性能。

4）重复步骤3），不断增加卸载点的个数，直至其最优卸载力使得光机系统满足各项指标要求。

设系统的可行卸载点集为SF，已添加的卸载点集为SF0，光机系统的优化目标所对应的位置点集为SD，从系统位移矢量d到优化目标值的转换函数为f2。每次从可行卸载点集SF中提取1 个或1 组卸载点，且该卸载点不属于SF0，保证原系统在增加该卸载点后的最优卸载力使得集合SD中所有位置的最大优化目标最小。设第i次施加的卸载点为Pi，则Pi须保证

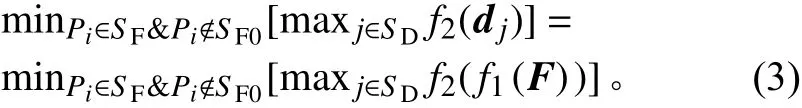
一般情况下，f2为计算某个光学镜的位置函数或面形函数。

利用贪心算法进行系统最佳卸载点系提取的算法复杂度为O(n)，而穷尽所有可行卸载点系找寻最优解的算法复杂度为O(2n)，可见利用贪心算法可以极大降低计算复杂度；同时由式(1)可知，求解模型为一近似的线性系统，一般情况下，施加较多卸载力的最佳卸载点系包含施加较少卸载力的最佳卸载点系，因而能保证该算法的高效性。

1.3 天牛须搜索算法

天牛须搜索算法是一种模拟天牛觅食的仿生算法。在自然界中，天牛觅食时利用左右触须来探测食物气味，从而获取下一个飞行方向。在多维空间搜索优化过程中，假设天牛在任意位置的方向是随机的，在某初始随机化位置，首先计算左右触须的位置，然后将位置值代入系统模型获得左右触须探测到的气味值，再根据气味值的大小判断天牛下一步的飞行方向，同时指定飞行步长，即可计算出天牛的下一位置坐标。由于天牛须搜索算法每次计算时只考虑一个个体，故具有较高的计算效率，尤其随着搜索维度的增加，相比于其他算法，其在计算效率方面的优势更加明显，能更高效、快捷地进行系统寻优。但是在该算法中，设置不同的初始位置、不同的触须距离、不同的迭代步长等均可能导致算法收敛于局部最优点；可在优化过程中调节相应参数，例如迭代步长，以提高算法的全局优化精度[10-11]。

给定一组卸载点系，设其卸载点的个数为k，天牛的第n次位置为Fn，天牛的朝向为Dn，天牛左右触须的探测距离为l。其中，Dn为k维随机归一化矢量。则：

一般情况下，天牛的触须探测长度l与步长step 为同一个数量级，以保证天牛的位置收敛方向与天牛须的探测收敛方向一致，因此令

将式(9)分别代入式(4)和式(5)可得：

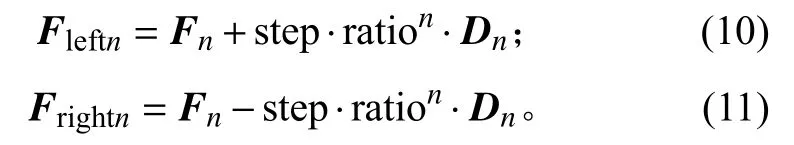
对比式(8)、式(10)、式(11)可知，按照式(9)的方式设置天牛须探测长度，天牛的下一位置为左须和右须探测到的最优位置，可简化搜索流程。

2 算法验证

2.1 测试结构模型搭建

以国内某遥感相机次镜的重力卸载仿真计算为例，验证本文所提出的算法。该遥感相机次镜的各项指标要求极高，基于其基本结构形式，搭建如图1 所示的近似光机主体结构，由主承力板、前镜筒和次镜组成，其最大外包络直径为2000 mm、长度为2600 mm。一般情况下，相机结构的刚度越低，在重力作用下的变形会越大，重力卸载仿真的难度会增大。为了更充分地验证算法的有效性，在搭建近似光机主体结构时进一步降低其刚度，仅采用简易的环形梁和横梁来搭接其前镜筒；次镜口径350 mm、质量3.5 kg，用直径10 mm、厚度2 mm 的空心管连接到前镜筒上；主承力板及前镜筒的材料一般选用密度较小、弹性模量较高的C-SiC 复合材料，本文为了增加分析难度，将其设置为钛合金。

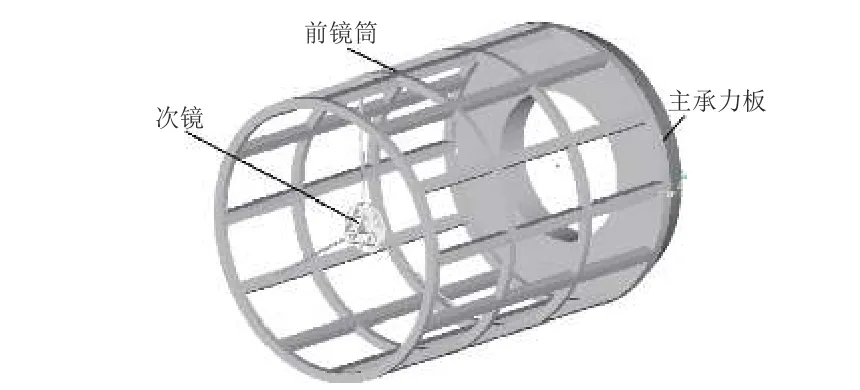
图1 光机结构组成Fig. 1 Configuration of the opto-mechanical structure

光机结构装调测试状态如图2 所示，以主成承力板两端为固定约束边界条件。

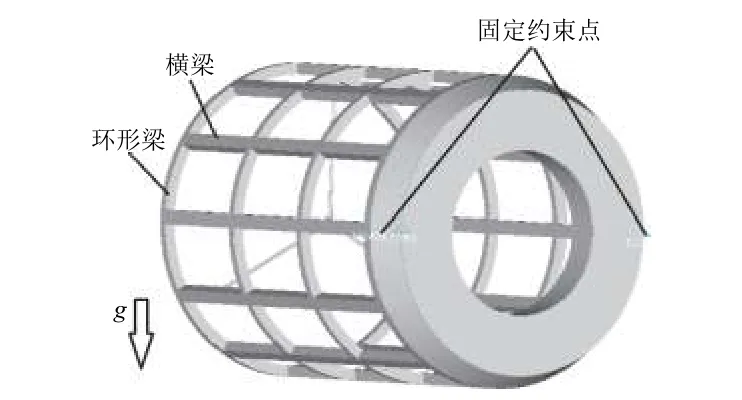
图2 光机结构装调状态Fig. 2 Assemblage of the opto-mechanical structure

考虑到测试过程中的实施误差，设定仿真目标为次镜的面形RMS 不大于(6/1000)λ，位置变化小于1 μm，角度变化小于1″。

2.2 测试模型刚度分析

建立该测试结构的有限元模型，施加固定位移约束条件及重力载荷。在不施加任何卸载力的情况下，次镜的结构位移为0.73 mm，如图3 所示。

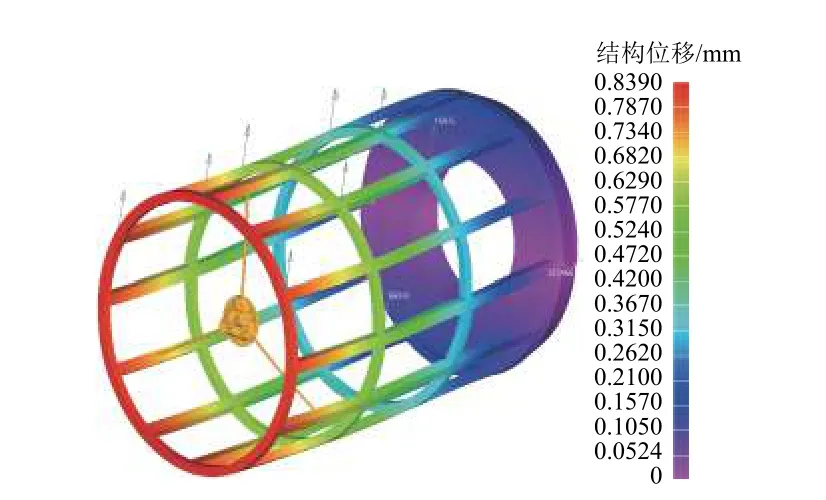
图3 测试模型无卸载力情况下的结构变形Fig. 3 Distortion of the test model without unloading force

该测试模型在固定约束边界条件下的前3 阶约束模态分别为10.9 Hz、19.6 Hz、27 Hz，如图4 所示。可以看到，该测试模型在重力作用下变形较大，其自由模态和约束模态都较低，即整体刚度较低。而一般情况下，光机结构在重力作用下的变形小于0.4 mm，一阶模态不低于30 Hz，因此利用该模型可充分验证算法的有效性。

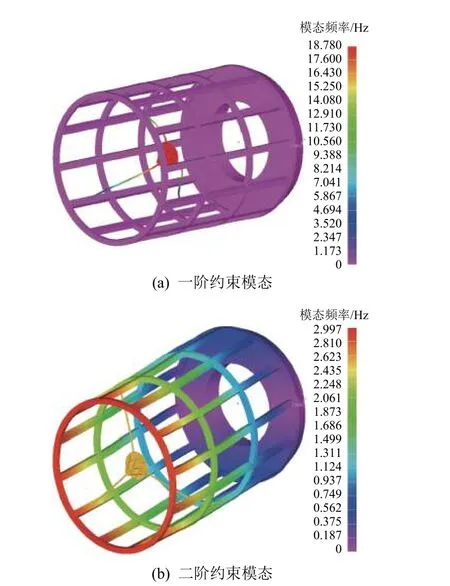
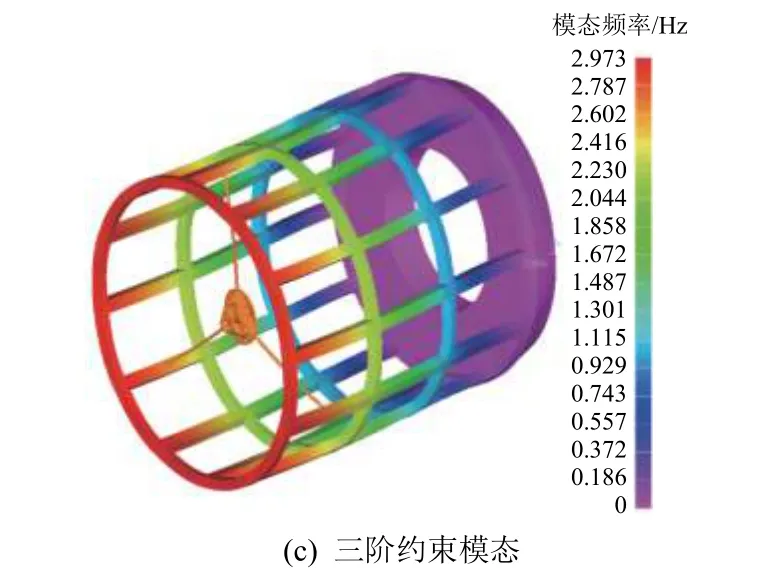
图4 测试模型的前3 阶约束模态Fig. 4 First three constrained modes of the test model

2.3 多目标优化分析处理

由于光学镜的面形RMS、位移及角度偏差需同时满足指标要求，而天牛须搜索算法中的方向判据为单个指标，所以需利用主目标函数法，提取主要优化目标，将其他优化目标作为约束条件。

光学镜的面形RMS 及角度偏差均由光学镜的位移变化而产生，故一般情况下，光学镜的位移偏差较小时，其面形RMS 及角度偏差均较小，因此本文提取光学镜的位移偏差为主目标，面形RMS 及角度偏差作为约束条件。在该计算分析过程中，f2设置为计算次镜的最大位移变化，以次镜的面形RMS 及角度变化作为收敛计算的判据。

2.4 仿真算法平台搭建及求解

在该测试模型的验证过程中，有限元仿真软件选取Femap，算法开发环境选取vs 2010 MFC 开发平台，基于式(3)、式(6)～式(8)、式(10)和式(11)，利用C++语言编写基于贪心算法结合天牛须搜索的空间相机地面装调重力卸载仿真计算程序，并利用Femap 提供的ATL 开发包建立MFC 与Femap的通信接口，以设置Femap 的加载力，控制其仿真计算并提取计算结果，完成整个算法模型的搭建。仿真算法平台界面如图5 所示。

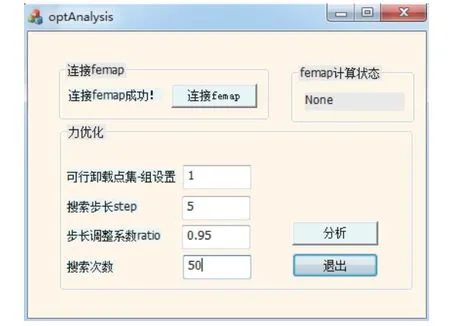
图5 仿真算法平台界面Fig. 5 The interface of the simulation platform

在该测试光机结构中，可行卸载点集选取前镜筒12 根横梁与3 个环形梁的交叉点，共36 个点。考虑到结构的对称性，以相机竖直中心面对称的每2 点组成1 组，故可行卸载点集中共有21 组卸载点。在天牛须搜索法中，搜索步长step 设置为5 N，步长调整系数ratio 设为0.95，每轮搜索次数设为50 次。

利用该仿真算法平台，经过5550 次迭代搜索计算得到，共需添加6 组卸载力，卸载点分布如图6所示。在该卸载力下，次镜最大位移0.6 μm，面形RMS 变化(1/1000)λ，角度变化0.5″，均满足指标要求。光机结构的变形如图7 所示。仿真计算得到的卸载力大小如表1 所示。

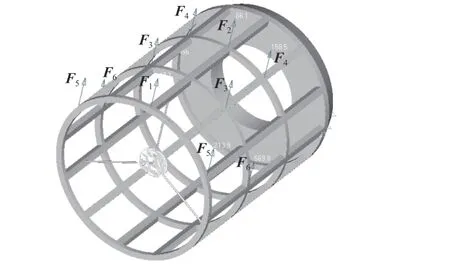
图6 仿真计算得到的重力卸载点分布Fig. 6 Unloading points distribution calculated by simulation

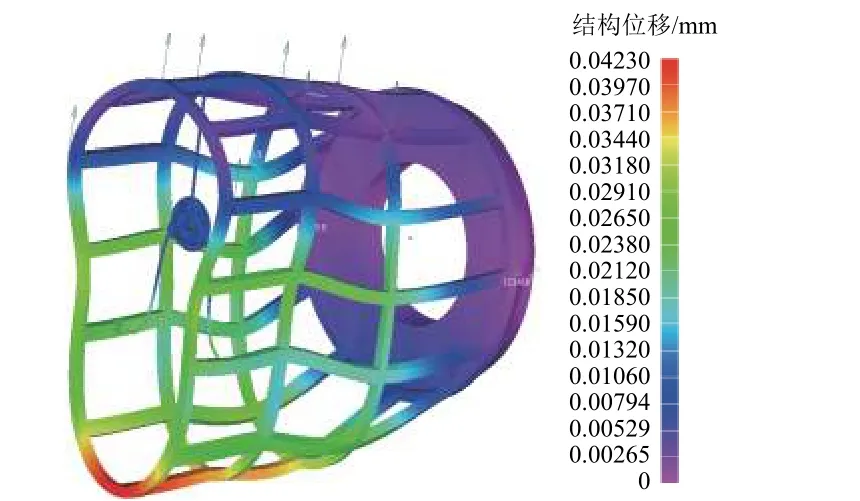
图7 测试模型在重力卸载后的结构变形Fig. 7 Structural distortion of the test model with unloading forces

表1 仿真计算得到的卸载力大小Table 1 Values of the unloading forces calculated by simulation单位：N

3 结束语

重力卸载的仿真优化是空间相机地面装调的难点之一，通过人为试错和调试的方法进行仿真优化计算，往往需要数日甚至数月的时间才能获得满足指标的解。本文提出一种基于贪心算法结合天牛须搜索的重力卸载仿真优化方法，通过计算机智能化迭代计算分析表明，在无须人为干预的情况下，在数小时之内即可获得满足系统指标的解，可以高效、快速地获得系统最佳卸载点系及最优卸载力，是解决空间相机地面装调时重力卸载仿真优化的有效方法。