超声速半球形多孔探针大气脱体激波仿真研究
张阳春,周树道,2,姚 韬
(1.国防科技大学 气象海洋学院,江苏 南京 211101;2.南京信息工程大学 气象灾害预警与评估协同创新中心,江苏 南京 210044)
1 引 言
半球形多空探针是一种适用于大气三维流场探测的传感器,具有结构简单、灵敏度高等优点,其外形呈球头-圆柱体结构。多孔探针的传统标定方法是基于探针孔压的多项式函数拟合法,这种方法是在不考虑探针头部绕流模型情况下建立起来一种风速、风向与孔压间的多项式函数关系,其标定精度主要取决于探针孔数和多项式阶数,标定过程也依赖于大量的风洞实验,成本较大[1~4]。目前针对多孔探针的研究大多是在亚声速下,在超声速和可压缩条件下的研究较少。为改进多孔探针的标定方法,提高测量精度和范围,降低标定成本,需要对多超声速条件下探针头部流体绕流流场进行研究,对超声速大气条件下探针头部脱体激波的研究必不可少。
针对超声速下钝头体脱体激波形状和脱体距离的研究,国内外学者以大量实验数据为基础得到了各种工程算法,并发现不同的工程算法只在自身实验条件下适用[5~9]。本文采用CFD方法,针对半球形探针在超声速大气条件下产生的脱体激波形状及位置开展研究,在1.2~1.7马赫数条件下进行数值仿真,使用最小二乘法进行数据处理,发现了脱体激波形状与脱体距离受马赫数的影响规律,建立了半球形探针在超声速下脱体激波曲线的参数化方程。
2 探针外形和网格
2.1 多孔探针结构
半球形多孔探针尺寸较多,以王偲臣等提出的一种可用于叶轮机内部流场测量的半球形高频气动五孔探针为例[10],探针正面及剖面图如图1所示,其机构由头部的半球体和尾部的圆柱体构成,内部有5个平行于轴线的测压孔,测压孔直径是探针直径的1/10。在研究探针头部脱体激波时,考虑到测压孔的孔径较探针直径而言很小、孔内部与外界间气体通量为零,且脱体激波与探针表面有一定距离,因此可以忽略测压孔的影响,将探针看作由半球和圆柱体组成的实心几何体,在此基础上对流场网格进行划分。

图1 半球形多孔探针结构图Fig.1 Hexical porous probe structure diagram
2.2 网格处理
当迎角为0°时流场在空间呈轴对称分布,仅对四分之一流场仿真即可。图2(a)所示为四分之一流体仿真域,边界包括出口、入口、壁面、对称面和探针表面,仿真域内存在比较均匀的自由流和速度、压强、密度、温度等物理量梯度较大的激波,使用自适应和误差估计功能,基于内置误差估计自动调整网格尺寸的自适应网格划分方法可以很好的预测激波的位置并解析激波[11]。在常规尺寸网格基础上对于激波位置处建立细化的网格,得到的自适应网格,计算网格数约50万个,网格顶点约9万个。图2(b)所示为网格划分后的探针表面和对称面,图中网格的疏密程度变化反映了流场中不同位置处物理量的梯度大小。

图2 流体仿真域和自适应网格Fig.2 Fluid simulation domain and adaptive grid
3 数值方法及验证
3.1 控制方程组
在马赫数大于0.3的情况下,须考虑气体的可压缩性,研究脱体激波现象可认为气体是无粘可压缩的[12]。N-S方程(Navier-Stokes方程)是描述粘性流体动量守恒的运动方程,忽略方程中的粘性项后可用来描述无粘流体。流体的可压缩性可以用连续性方程描述。激波的产生会使气体温度发生剧烈变化,建立控制方程组时必须考虑气体动能与内能之间的转化。鉴于此,得到适用于气体激波无粘可压缩流体控制方程组如下:
(1)

(2)
(3)
p=ρRT
(4)
e=γT
(5)
式(1)为N-S方程忽略粘性项时的无粘流体动量方程,式(2)为可压缩流体的连续性方程,式(3)为流体能量方程,式(4)为气体状态方程,式(5)为气体内能公式。其中:ρ是流体密度;t是时间;u是流体速度矢量;e是气体内能;p是气体压强;R是气体常数;γ是气体比热比;T是气体温度。
同时假设流体在壁面和探针表面满足绝热和滑移(无摩擦)条件:
nu=0
(6)
nq=0
(7)
式中:n是壁面和探针表面法相单位矢量;q是热量。
3.2 数值方法和算例验证
基于目前的全球大气观测数据,对流层顶气压场介于100~320 hPa之间[13],以300 hPa、273 K大气环境值为数值模拟的计算工况,采用有限元方法对式(1)~式(5)所示的控制方程组进行离散,为提高计算效率采用三次迭代求解,边界条件取远场边界无反射边界条件,探针表面和壁面为无摩擦滑移、绝热,全场取自由来流值为初始条件。自由来流速度在1.2到1.7马赫之间,每间隔0.1马赫做一组数值采样。
图3是来流马赫数为1.5、攻角为0°时探针表面和对称面的速度、压强云图,在探针头部流体的速度和压强出现明显的弧形间断面,脱体激波位置和形状清晰可见,探针尾部形成尾流和斜激波,仿真流场与实验现象相符。
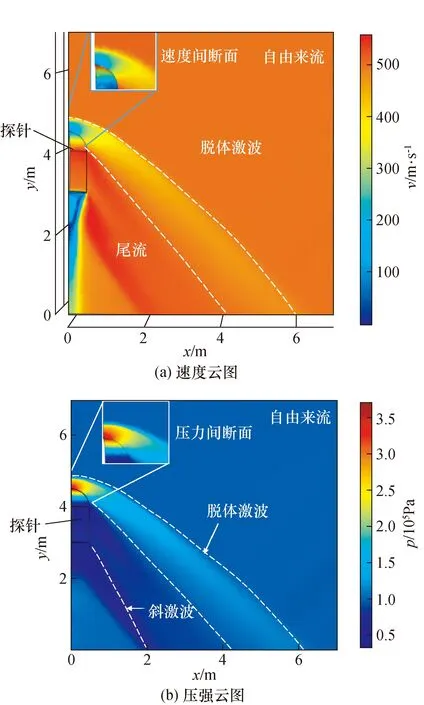
图3 速度和压强云图Fig.3 Velocity and pressure cloud
3.3 数据提取与处理
为得到激波曲线的具体位置,需要对仿真数据进行筛选。流体经过激波时压强突增,压强梯度云图可以很好地识别激波,在数值仿真得到的流场压强云图基础上对压强求梯度得到如图4(a)所示的压强梯度云图。从图中可以看出脱体激波在球头处呈弧线分布,沿直线向无穷远处延伸,与球面间的距离为脱体距离。
将网格节点数据导出并重新绘制得到如图4(b)所示的压强梯度节点离散图,各节点的值代表节点处压强梯度。按照一定的阈值将压强梯度值较小的节点,即与激波曲线相关性较弱的节点剔除,得到如图4(c)所示的与激波位置相关性较高的节点离散图,作为激波曲线采样点。
4 激波曲线拟合
在超声速且迎角为零时,球-圆柱体形成的激波形状为一轴对称曲面,子午面如图5所示,研究这一曲面只需考虑子午面的母线即可。来流马赫数Ma=1时球-圆柱体头部脱体激波是一无限远处的直线,随着Ma的增大,激波的脱体距离D和曲率半径R逐渐缩小,在球面处形成一条间距极窄的圆弧段,后沿以直线向无穷远处延伸,这一特征与双曲线类似,激波脱体距离和曲率半径可看作马赫数的单值函数。
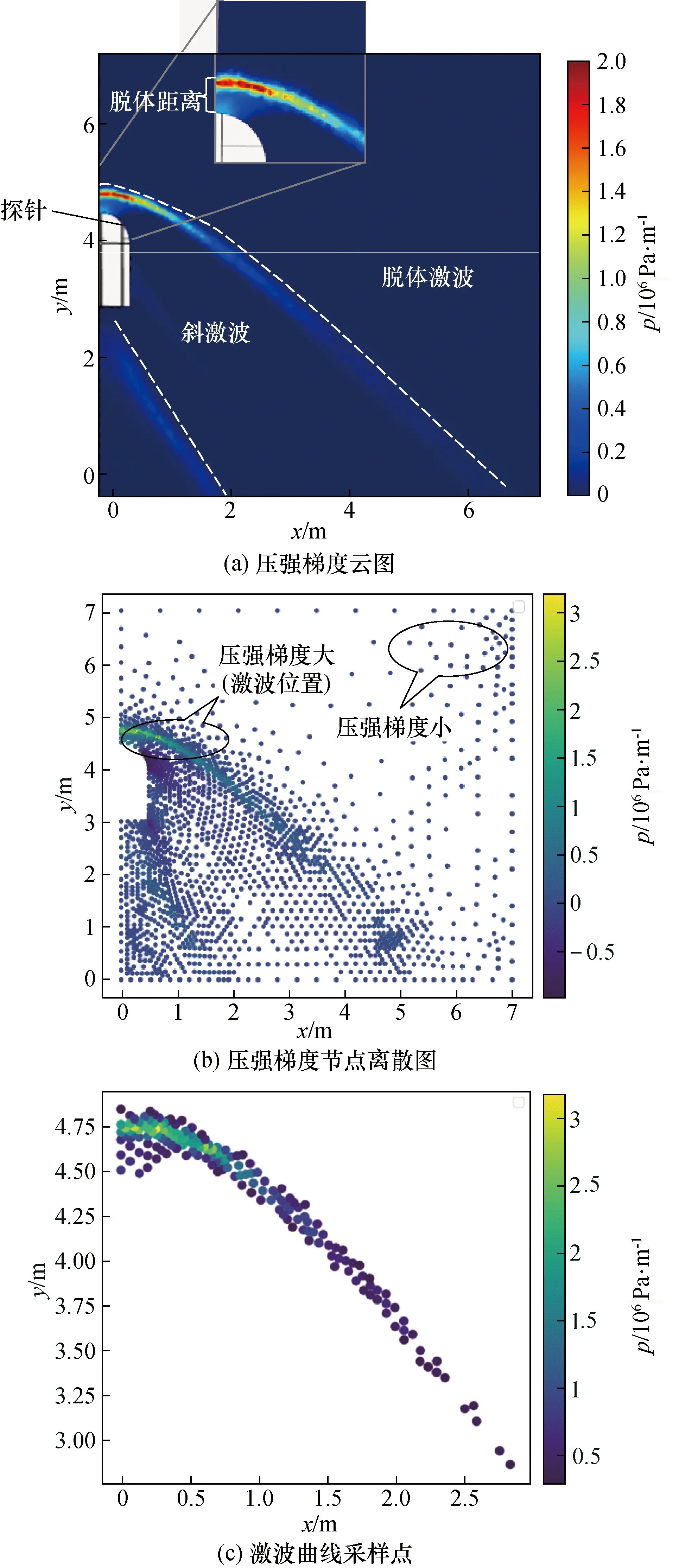
图4 数据处理过程 Fig.4 Data processing

图5 脱体激波直角坐标关系Fig.5 Schematic diagram of detached shock wave
郑之初等使用了曲率中心位于球心的一组圆锥曲线来表示激波形状[14]。考虑到曲率中心与球心并不必然重合,将曲率半径和脱体距离分别看作Ma的单值函数,分别拟合激波的位置和形状,使用如图(5)所示的以球心为原点的双曲线直角坐标参数化方程表示脱体激波,其表达式为:
(8)
(9)
(10)
D=|a+d|-1
(11)
式(8)为激波曲线的直角坐标参数化方程。其中:x、y表示激波曲线上的点到坐标轴的距离;r为球体半径;x/r、y/r表示将激波曲线以r为单位长度等比例变化;a、b、d为待求解的未知量。
式(9)、式(10)、式(11)分别表示激波曲线的离心率e、曲率半径R和脱体距离D与未知量a、b、d之间的关系。将e、R、D看作马赫数Ma的单值函数,基于仿真数据拟合可得到e、R、D与Ma间的函数关系。对任意给定的Ma,联立式(9)、式(10)、式(11)可得到式(8)中未知量a、b、d的值,代入式(8)中,任意Ma对应的激波曲线都得以确定。
4.1 参数拟合
在1.2到1.7马赫范围内进行6组数值仿真,以不同马赫数时激波曲线的采样点为样本数据,如图4(c)所示,式(8)为回归模型,采用最小二乘法拟合不同马赫数时的激波曲线,得到公式中参数的估计值,拟合结果如图6所示,样本点大于200个,参数a、b、d的拟合方差如表1给出。

表1 参数a,b,d拟合方差Tab.1 Fitting variance of parameters a,b and d
由图6拟合曲线中的参数a、b、d的值及式(9)、式(10)、式(11)计算得到不同马赫数时参数e、R、D的值。
图7给出了离心率e、曲率半径R、脱体距离D在不同马赫数下的值和各参数与马赫数Ma的函数关系拟合曲线。

图6 激波曲线拟合Fig.6 Shock curve fitting
拟合结果显示随着马赫数的增大激波离心率、曲率半径和脱体距离呈下降趋势,且下降速度逐渐减缓,这与实验现象相符。参数e、R、D的具体拟合公式为:
(12)
(13)
(14)
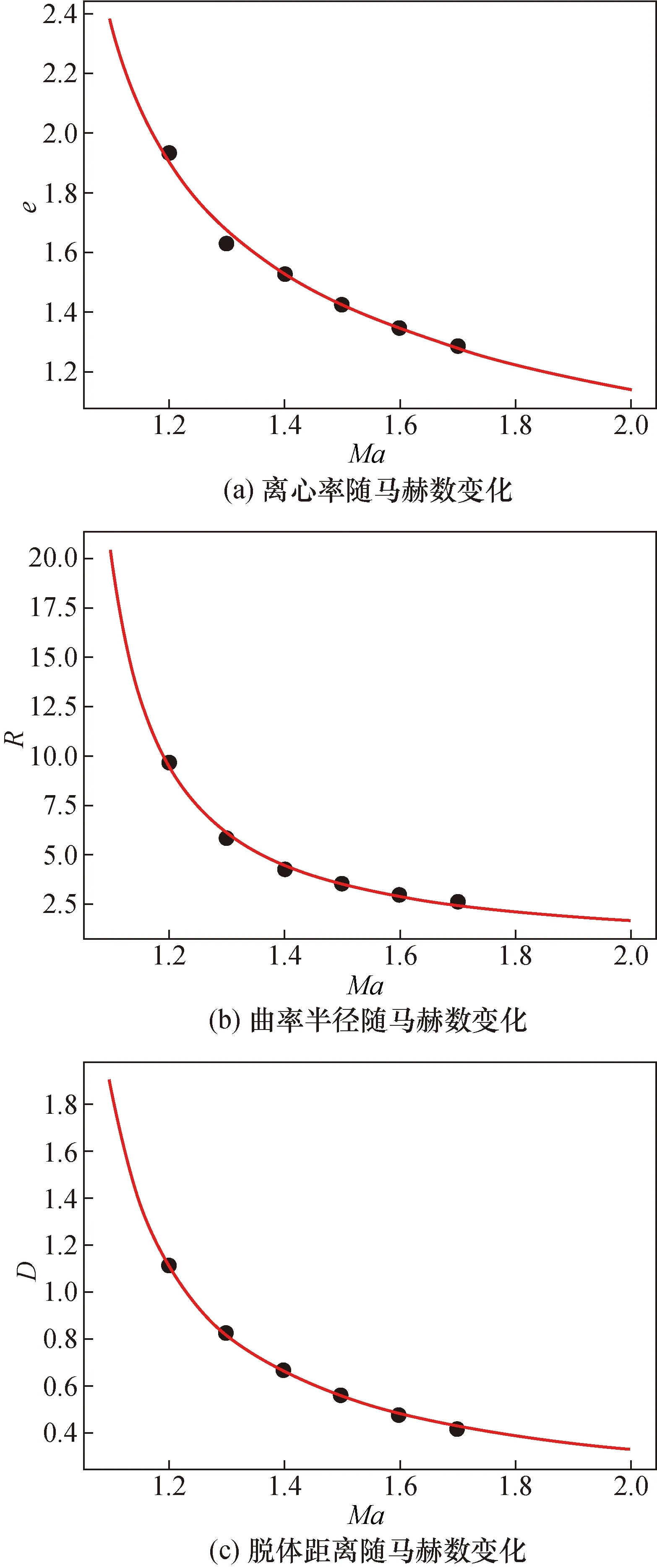
图7 参数与马赫数拟合曲线Fig.7 Fitting curve of parameters and Mach number
4.2 结果比较与分析
对不同的马赫数Ma和球体半径r,联立式(9)、式(10)、式(11)、式(12)、式(13)、式(14)可得参数a、b、d的值,代入式(8)中得到由参数化方程预测的激波曲线。
图8是本文得到的激波参数化方程曲线与仿真得到的对称面压强梯度云图的对比,在1.2~1.7马赫内,由参数化方程给出的曲线与仿真结果极为相符。

图8 对称面压强梯度云图与参数化方程曲线对比Fig.8 Symmetrical face pressure gradient cloud chart is compared with the paramethy equation curve
Billig基于试验数据提出一种适用于球头-圆柱脱体激波形状的经验公式[15],该公式适用于较低温度下的理想气体状态。
图9将经验公式与本文得到的参数化方程进行了比较,从图9中可以看出,当流速介于1.2~1.4马赫之间时2条曲线重合度较低,在1.5~1.7马赫之间时两曲线重合度较高。在同一马赫数下,距离球面越近曲线重合度越高,随着曲线远离球面重合度降低。两条曲线对激波脱体距离的预测基本一致,预测结果的差值小于球体半径的5%。
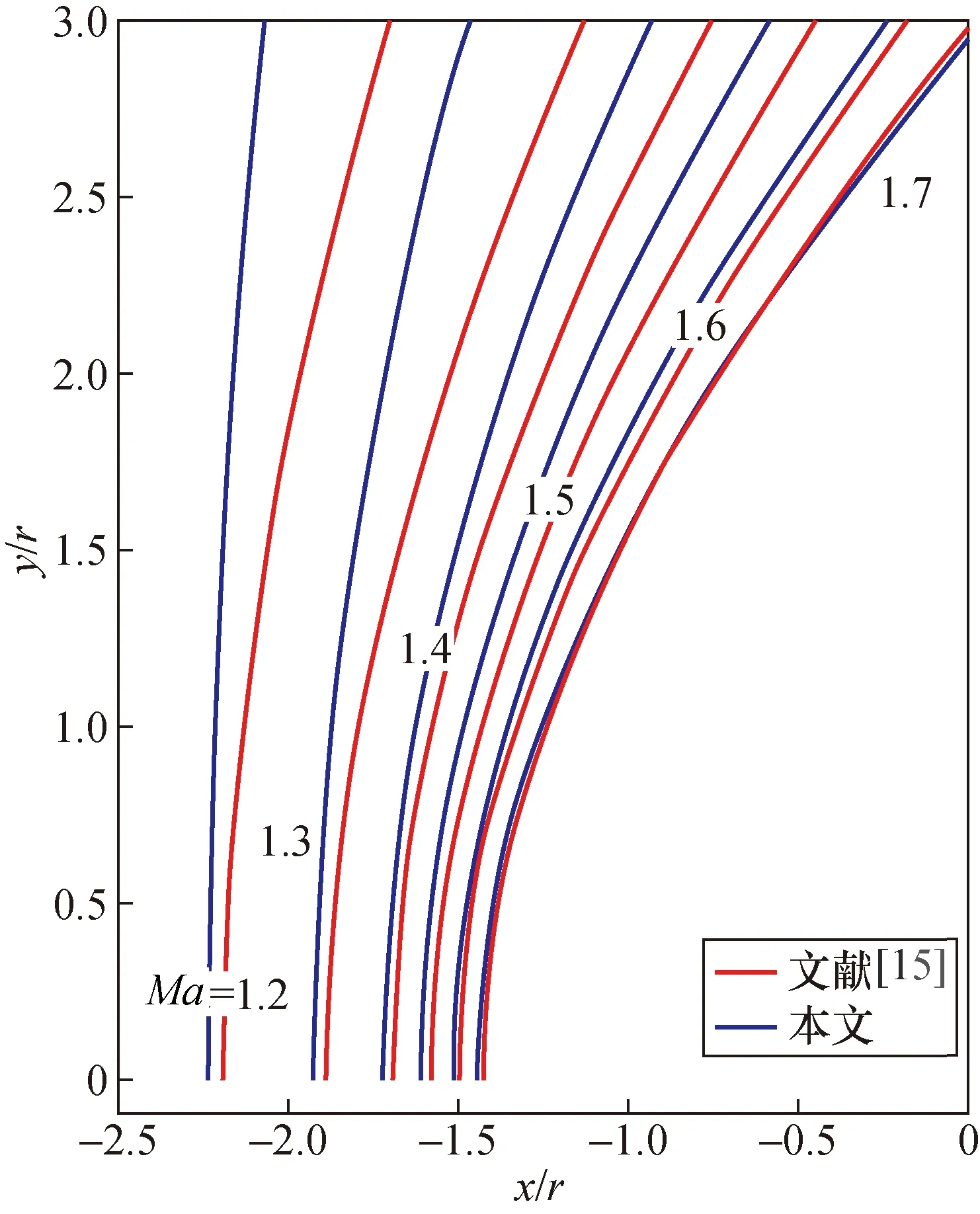
图9 脱体激波随马赫数变化Fig.9 Changes of oobody shock wave with Mach number
距离头部较近的曲线重合度高的原因,是在处理数据时,按照压强梯度值来选取节点的,由于距离较远处的激波强度小,尤其当马赫数较低时激波强度衰减更快。节点处压强梯度达不到阈值而被剔除,最终的拟合曲线更加接近球头-圆柱体头部强度较大的激波的形状。说明该参数曲线对于近球面激波情况更加适用。
5 结 论
本文采用数值计算仿真了半球形多孔探针在超声速大气条件下的脱体激波,并研究了脱体激波形状和脱体距离受大气流体马赫数影响规律。得到了在1.2~1.7马赫范围内与数值仿真结果一致性较好的激波曲线参数化方程,方程对激波脱体距离预测准确,在近球面处精度更高。

