基于VMD能量熵与优化支持向量机的轴承故障诊断

金江涛，许子非，李 春,2，缪维跑，李 根

(1.上海理工大学 能源与动力工程学院，上海 200093；2.上海市动力工程多项流动与传热重点实验室，上海 200093)

1 引 言

滚动轴承作为机械设备中重要传动部件之一，其运行状态直接影响整机设备的健康状况。为减少轴承发生故障所造成经济损失，对滚动轴承进行早期故障诊断尤为重要[1]。目前，信号采集、特征提取及状态分类构成故障诊断框架，特征提取有效性与状态分类准确性直接影响故障诊断结果。

振动信号因具备易采集，包含振动信息丰富及易处理等特点被广泛用于轴承振动分析。但轴承早期故障微弱且易被噪声淹没，故障特征提取较为困难，从而影响故障诊断准确性[2]。此外，由于机械系统振动耦合与复杂环境影响，振动信号具有非线性和非平稳的特点，仅从时域、频域或时频域角度难以分析、判别故障类型[3]。目前主要有小波变换(wavelet transform，WT)、经验模态分解(empirical mode decomposition，EMD)、集合经验模态分解(ensemble empirical mode decomposition，EEMD)以及变分模态分解(variational mode decomposition，VMD)等方法对振动信号进行预处理[4～7]。WT方法因未明确小波基的选择和分解层数，缺乏自适应性。EMD的基函数以信号数据自适应分解所得，具备较好的分解效果，其能使非平稳数据平稳化，将分解所获本征模函数(intrinsic mode function，IMF)进行Hilbert变换得到具有物理意义的频谱，但其存在模态混叠和端点效应两大弊端[8]。为此，提出了基于EMD的改进方法EEMD：通过引入高斯白噪声减弱模态混叠现象，对信号具有优良的自适应性和时频分辨率，但剩余噪声会引起信号重构误差，从而影响特征提取有效性。而变分模态分解算法，因其完备的数学基础及求解方式，改善了端点效应和模式混叠现象，从而保障了特征提取的有效性[9]。

Huang Y等[10]通过改进尺度空间以提高VMD的适应性，在一定范围内引入中心频率可提高原始VMD的计算速度。Dong W等[11]结合VMD与奇异值分解法对故障特征进行提取，结果表明该方法可准确处理轴承故障诊断问题。文献[12]采用VMD与Hilbert边际谱能量熵的特征提取方法，输入支持向量机中进行状态分类，结果表明该方法可准确识别机械故障类型。文献[13]采用VMD与最小熵反褶积结合以滤除噪声，并进行Hilbert包络解调分析，可有效提取早期故障信号中微弱特征信息。

支持向量机(support vector machine，SVM)作为机器学习主流算法之一，可解决小样本、非线性及高维问题，在故障状态分类上具有良好表现[14,15]。Zhang M J等[16]将改进EEMD与SVM结合，可实现低维小样本下的智能故障诊断。文献[17]提出多维度互近似熵的特征提取方法，并输入SVM中进行状态分类，结果显示该方法可准确区分轴承不同类型及程度的故障。文献[18]采用改进的固有时间尺度分解和样本熵的特征提取方法，输入SVM中识别故障特征，研究发现：相比BP神经网络，该方法具有更高的故障识别准确率。文献[19,20]采用VMD对振动信号进行分解，分别通过遗传算法(genetic algorithm，GA)和粒子群优化算法(particle swarm optimization，PSO)优化SVM参数，提升了故障识别准确率。

由于惩罚因子c、核函数参数g对SVM分类效果影响显著，而灰狼算法(GWO)具有原理结构简单、全局搜索能力强以及泛化能力强等优点，且在收敛速度与精度上均优于PSO和GA算法，故采用GWO优化SVM参数以提升故障类型识别准确率。

故障诊断成功与否取决于特征提取有效性与状态分类准确性[21]。现有研究中，特征提取过程采用时频分解与特征值组合的方法，未考虑时频分解本身为特征提取的重要环节，分解算法与特征值的统一性对特征提取精度有显著影响。本文借鉴EEMD递归特性，基于VMD与能量熵提出一种新的特征提取方法，以构建多模态特征矩阵。同时考虑SVM参数对分类器泛化能力的影响，采用GWO优化其参数，实现基于VMD-Entropy-OSVM的智能故障诊断方法。通过轴承振动实验验证所提出方法在噪声环境下的有效性。

2 基于VMD信号特征提取

2.1 VMD算法

VMD可有效抑制EMD类产生的端点效应和模态混淆现象，其可分解为若干调幅-调频(AM-FM)信号，表达式如下：

uk(t)=Ak(t)cos(φk(t))，k=1,2,…,K

(1)

式中：uk(t)为各模态信号；Ak(t)为瞬时幅值，且为非负包络函数；φk(t)为信号相位；K为模态分解个数。

变分模型构建需要以下几个步骤：

1)先经Hilbert变换，得到每个IMF解析信号，然后再得到信号单边频谱：

(σ(t)+j/π t)·uk(t)

(2)

式中：σ(t)为单位脉冲函数；j为虚数单位；t为时间。

2)引入指数项来调整各IMF估计中心频率ωk，调制每个IMF频谱到其相应基频带：

((σ(t)+j/π t)·uk(t))e-jωkt

(3)

3)根据解调信号梯度的平方L2范数，估计各IMF带宽，则所构造的约束变分模型为：

(4)

式中：∂t为偏导运算；*表示卷积运算；{uk}={u1,u2,u3…,uK}表示VMD分解得到的K个IMF分量；{ωk}={ω1,ω2,ω3，…,ωK}表示各模态分量的中心频率。

为将问题转变为非约束性变分求解，VMD在求解过程中通过引入惩罚因子α及Lagrange乘子 λ(t)来获得VMD最优解。扩展后的Lagrange表达式如下：

(5)

(6)

(7)

(8)

式中：τ为保真系数；^表示傅里叶变换；n为迭代次数。在求解变分模型时，IMF分量的中心频率与带宽不断更新，直至满足迭代停止条件，其表达式如下：

(9)

式中：ε为判别精度，本文取10-6。

2.2 信号特征提取

由于VMD算法不具备递归性，需预先确定模态分解数K和限制带宽因子α。借鉴EEMD算法递归特性[22]，考虑故障特征频率多处于低频段，以模态能量熵最大作为寻优目标，在低频段求解最佳α。此方法比传统人为经验设置VMD参数具有更可信的分解精度，与双参数寻优方法相比具有更快的计算速度。为获取准确有效的故障特征，构建准确地特征向量以保证状态分类的准确性。采用参数优化后的VMD，基于IMF能量与能量熵构建多模态特征矩阵。

3 基于VMD -Entropy -OSVM的轴承故障诊断

GWO算法[23]具有原理结构简单、编程容易、全局搜索能力强等优点，且在收敛速度与精度上均优于PSO算法和GA算法[24]。因此本文采用GWO算法对SVM参数进行寻优。

3.1 OSVM参数选取

SVM中惩罚因子c调整了样本误分类比例和算法复杂度之间的权衡，而参数g为内核函数的宽度，控制要素子空间分布的复杂性。显然，这两参数对SVM最终模式识别结果有较大影响。因此，为提高SVM的学习、泛化能力，采用GWO算法以确定最佳参数，其实现流程如图1所示。

图1 OSVM参数流程图Fig.1 Flow chart of OSVM parameters

3.2 故障诊断流程

采用优化后的VMD对原信号进行分解，基于各IMF能量与能量熵构建多模态特征矩阵，输入SVM中进行网络训练，将筛选得到的最佳参数c和g用于测试集，计算故障分类准确率。基于VMD-Entropy-OSVM轴承故障诊断流程如图2所示。

图2 故障诊断流程图Fig.2 Flow chart of the fault diagnosis

4 实验分析

为验证基于VMD-Entropy-OSVM轴承故障诊断方法的有效性，通过轴承振动实验数据，研究所提出方法在噪声环境下诊断表现。

4.1 实验装置

轴承加速寿命实验平台如图3所示。

图3 轴承加速寿命实验平台Fig.3 Bearing accelerated life test platform

实验平台主要由交流电动机、液压加载系统、转速控制器、传感器、轴承和转轴等组成，可对滚动轴承各工况下的加速寿命进行实验，获取测试轴承的全寿命周期监测数据。设置采样频率为25.6 kHz，分别采用转速为2 100和2 250 r/min的工况进行实验。本文将加速度传感器固定于轴承的竖直方向上，采集4种故障下的信号数据。滚动轴 承 相 关 参数见表1、轴承加速寿命实验工况见表2[25]。

表1 轴承参数Tab.1 Bearing parameters

表2 轴承加速寿命实验工况Tab.2 Bearing accelerated life test conditions

3种故障类型的轴承图片，如图4所示。

图4 3种故障类型的轴承图Fig.4 Bearing diagram of three failure types

将轴承全寿命周期监测数据分为初期、中期和末期3个阶段。通过时域图可分析各阶段所含差异，其时域图如图5所示。

图5 轴承在各阶段不同故障下的时域图Fig.5 Time domain diagram of bearings under different faults in each stage

由图5可知，轴承各阶段不同故障下的振动信号有所不同。以保持架磨损为例，在故障发展初期，中期和末期其振幅最大值分别为5.75 m/s2，6.93 m/s2，27.78 m/s2，可见随着故障发展，振动幅值逐渐增大。因此通过幅值大小可判断轴承故障所处阶段。

为判断轴承故障类型，采用合理有效的特征提取方法尤为重要。因故障特征信号多处于低频段，故以20为步长，在[500,1 500]搜寻最优参数α。各故障信号的VMD分解参数见表3。

各故障类型分别采集20组信号，40组作为训练样本，40组作为测试样本，每组信号样本长度为4 096，采用VMD对原始信号进行分解，计算前8个IMF的能量与其能量熵值，构建40×9的多模态特征矩阵，输入SVM中进行状态分类，结果如图6所示。

其训练样本特征向量集见表4，由于篇幅所限，仅列出10个样本中3个样本的数据，pi(i=1,2,…8)为各模态能量，H为能量熵值。

采用OSVM时其分类结果如图7所示。

表3 各故障信号的VMD分解参数Tab.3 VMD decomposition parameters of each fault signal

由图6和图7可知，采用SVM在初期、中期和末期阶段分别有6个、3个和2个分类错误，而采用OSVM在这3个阶段均分类正确，体现了参数c和g对SVM的分类准确率影响显著。

表4 训练样本特征向量集Tab.4 Feature vector set of training samples

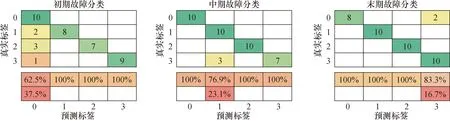
图6 采用SVM在不同阶段下故障分类结果Fig.6 Fault classification results in different stages using SVM

图7 采用OSVM在不同阶段下故障分类结果Fig.7 Fault classification results in different stages using OSVM

4.2 噪声对模型性能影响

由于轴承所处环境复杂，噪声无法避免，为验证模型在噪声环境下的准确性，在原始信号中加入一定比例的高斯白噪声，以模拟真实工业环境。

以轴承内圈磨损为例，对原始信号加入信噪比分别为0 dB、4 dB和8 dB的高斯白噪声，其时域图如图8所示。其中0 dB代表振动信号成分等于噪声成分。

图8 加入噪声的振动信号对比Fig.8 The original signal of inner race fault with white Gaussian noise

由图8可知，加入噪声后的振动信号将原始信号掩盖，幅值较未加噪声的振动信号更大。

在未加噪声情况下，其包络谱图如图9所示。

图9 无噪声下包络谱图Fig.9 Envelope spectrum without noise

由图9可知，由于该轴承数据在良好实验环境下测得，因此其故障特征频率较为明显。一倍转频为37 Hz，故障特征频率为118 Hz，与滚动轴承结构参数所计算的内圈故障特征频率相近。表明该数据在未加噪声情况下，可通过故障特征频率判别其故障类型。

图10为各信噪比下包络谱图，信噪比为0 dB、4 dB和8 dB下仅提取出一倍转频，而故障特征频率均已完全淹没，无法找出其特征频率，表明噪声对原始信号有较大影响，无法通过故障特征频率判别其故障类型。

图10 各信噪比下包络谱图Fig.10 Envelope spectra under each SNR

为验证本文VMD-OSVM模型在噪声环境中的优势，分别与EEMD-SVM、VMD-SVM、VMD-GA-SVM、VMD-PSO-SVM以及EEMD-OSVM 5种方法进行信噪比为0 dB至8 dB情况下，10次实验的平均诊断准确率对比，结果如图11及表5所示。对相对纯净信号(信噪比为8 dB)进行故障诊断，本文采用的VMD-OSVM方法有99.8%的识别准确率，比现有算法提高3.3%～27.3%。在处理信噪比为0 dB信号时的故障时，所提方法仍达73.5%的准确率，比现有算法准确率提高11%～33%。VMD相比EEMD为更好的时频分解算法，GA与PSO易陷入局部最优解，导致模型泛化性能较差，故障识别准确率低。说明同时考虑特征提取的有效性与分类器参数选取的可靠性，可提升故障诊断模型的泛化能力，因此VMD-OSVM方法在处理含噪信号时具有更高准确率。

图11 不同算法在各信噪比下准确率对比Fig.11 The accuracy comparison of different methods under different SNR

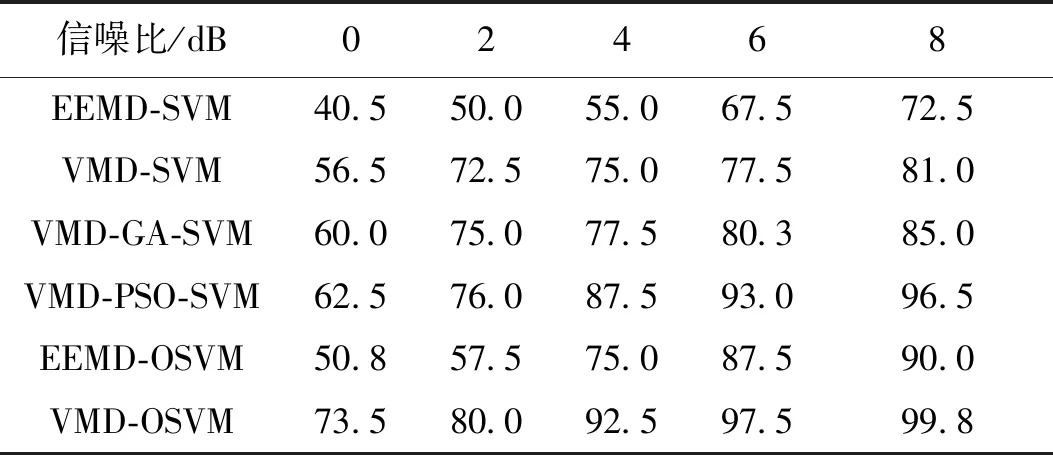
表5 不同算法在各信噪比下准确率对比Tab.5 The accuracy comparison of different methods under different SNR (%)

为凸显OSVM相比GA-SVM和PSO-SVM在收敛速度与精度上的优势，对每一步迭代的适应度值进行了分析，结果见图12。由图可知，OSVM算法在第9步迭代时完成收敛，且最终平均适应度值(即平均错误识别率)明显优于GA-SVM和PSO-SVM算法，证实了OSVM算法在参数选择上的优势。

为提升故障诊断效率更符合实际工程应用，体现基于多模态特征矩阵及OSVM构建智能诊断模型的计算效率，与现有算法进行对比，结果如表6所示。

表6 不同算法的运行时间Tab.6 Running time of different algorithms

由表6可知，OSVM平均运行时间为0.562 s，比GA-SVM和PSO-SVM分别快99.6%和213.2%。

因GWO算法具有的优势特点，使得其计算速度相比现有优化SVM算法更快。

5 结 论

本文借鉴EEMD递归特性，采用VMD算法与能量熵结合构建多模态特征矩阵，以GWO算法优化SVM参数，提出VMD-Entropy-OSVM轴承智能故障诊断，轴承实验数据验证了方法的有效性。

(1)采用VMD算法与能量熵结合构建多模态特征值矩阵的特征提取方法优于EEMD能量熵。

(2)本文算法不仅可识别轴承损伤末期的不同故障类型，且在识别损伤初期亦有较高准确度。

图12 不同算法的平均适应度曲线Fig.12 Average fitness curves of different algorithms

(3)在信噪比为8 dB下准确率高达99.8%，比现有方法提高3.3%～27.3%；当信噪比为0 dB情况下仍有73.5%的准确度，比现有方法提高11%～33%，该模型表现出良好的泛化性能。

(4)因GWO算法具有结构简单、概念清晰以及全局性能优等特点，使得其收敛速度与计算速度相比现有优化SVM算法更快。