一种调制度测量仪的数字化精确评价与溯源方法

梁志国，何 昭，缪京元，郭晓涛，张亦弛

(1.北京长城计量测试技术研究所 计量与校准技术重点实验室，北京 100095；2.中国计量科学研究院，北京 100029)

1 引 言

人们在分析利用信号波形时，通常涉及时域、频域、值域、调制域等不同维度的手段和方法。

在时域，人们使用波形采集记录，直接进行测量比较、分析，获取时域参数；主要是带时间定位的幅值和时间参量。

将时域波形通过傅里叶变换，映射到频域，获得其频域参数；主要是带频率定位的功率能量参量和相位谱参量。

对时域波形进行统计分析，获得其值域参数；主要是以幅值区间定位的出现概率值。

时域、频域和值域的计量问题均已解决，而调制域则不同。调制域的已调信号，通常是在选定的周期性载波基础上，以调制信号控制载波的某一参量，让受控参量随时间变化的规律与调制信号相一致而获得。目前最常用的载波信号是正弦波，其幅度、频率、相位分别按调制信号波形规律变化时，获得的已调信号波形被分别称为调幅(AM)、调频(FM)、调相(PM)信号。

调制域测量仪，是能从AM、FM、PM信号中解调出调制波形，并获得调制参数的仪器。由于其技术指标高于已调信号的指标，导致其计量校准一直未能获得完全解决。相应的国家计量技术规范[1]，使用“标准调制度测量仪”来校准“被校调制度测量仪”。但标准调制域测量仪的计量，一直无解。

本文后续内容，将主要讨论该问题，并试图找到一种方法，解决调制度测量仪的计量校准难题。

2 基本原理方法

所有AM、FM、PM信号源及调制度测量仪的共同点[2]，是载波频率通常远高于调制信号频率和调制产生的频偏，属于高频载波下的窄带调制信号波形，即窄带宽带限信号。因此，与载波相比，其参数随调制信号而变化的过程“非常缓慢”。载波周波在被调制后，仍然可以局部近似为正弦波。调制过程，即正弦载波波形参数的缓慢变化过程。

由此，可使用一个或少于一个载波的局部波形，以正弦波滑动拟合方式，提取出其幅度、频率、相位随时间变化的曲线规律，实现AM、FM、PM信号的解调。校准相应信号源和调制度测量仪的量值。过程如下：

如图1所示，信号发生器产生的已调信号通过功率分配器分为2路，一路到调制度测量仪进行调制分析测量；一路到数字示波器进行采集测量。

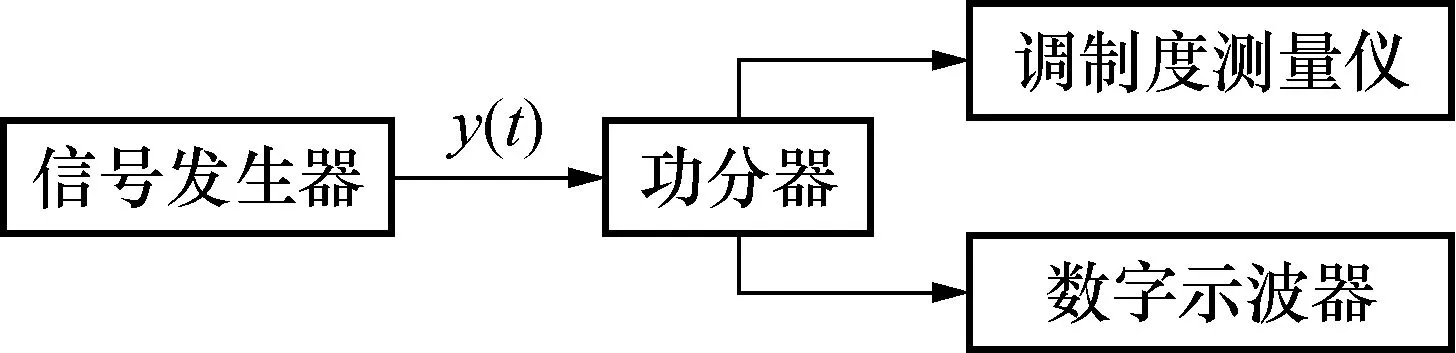
图1 调制度测量仪校准框图Fig.1 The calibration of modulation meters

设已调信号为y(t)，其瞬时幅度为A(t)，瞬时频率为f(t)，瞬时相位为θ(t)。对y(t)进行采样、量化和数据采集后，获得数据记录序列为时刻t1,t2,…,tn的采集样本y1,y2,…,yn，采集速率v，采样间隔Δt，ti=i×Δt=i/v，(i=1,…,n)。

2.1 AM信号解调

若y(t)是AM信号，按文献[3]所述对采集样本y1,y2,…,yn解调，获得幅度A(t)解调序列A1,A2,…,An。

通常，用信号发生器产生的AM信号，调制信号为幅度ΔA、频率Ωa的正弦波。对解调序列A1,A2,…,An使用四参数正弦波拟合法处理[4]，获得拟合幅度为ΔA、频率为Ωa、直流分量为C的估计值。

其四参数正弦拟合过程如下：

当采集序列中任意一个波形段{yi,yi+1,…,yi+m}被近似认为是正弦波y(t)。

y(t)=Ecos (2 π Ft+Φ)+Q

(1)

若频率F已知，可通过三参数最小二乘拟合[4]，由{yi,yi+1,…,yi+m}直接计算，获得参数E、Φ、Q的拟合值A、θ、C。

当频率F未知，但可通过波形判定其存在的区间[Fmin,Fmax]，通过对F在该区间内的一维搜索，获得频率F的拟合值f，完成四参数拟合[4]。

(2)

拟合残差有效值：

(3)

测量数据段的总失真度[5]：

(4)

当波形段{yi,yi+1,…,yi+m}由起始点y1至终点yn滑动时，获得不同的局域拟合值序列{Ai、fi、θi、Ci}。其中，{Ai}是幅度解调序列；{fi}为频率解调序列，(i=1,…,n)。并可计算解调波形的失真度[5]。

则可得调制幅度ΔA、调制频率Ωa、载波幅度C。调幅度为ΔA/C。以此作为标准值，可校准调制度测量仪的AM解调参数。

2.2 FM信号解调

若y(t)是FM信号，按文献[6]所述对采集样本y1,y2,…,yn解调，获得频率f(t)解调序列f1,f2,…,fn。

信号发生器产生的FM信号，调制信号为调制频偏Δf、频率Ωf的正弦波。对解调序列f1,f2,…,fn使用四参数正弦波拟合法处理[4]，获得拟合幅度为Δf、频率为Ωf、直流分量为fc的估计值。则得调制频偏Δf、调制频率Ωf、载波频率fc。以此作为标准值，可校准调制度测量仪的FM解调参数。

2.3 PM信号解调

若y(t)是PM信号，按文献[7,8]所述对采集样本y1,y2,…,yn解调，获得相位θ(t)解调序列θ1,θ2,…,θn，载波频率fc。

信号发生器产生的PM信号，调制信号为调制相偏Δθ、频率Ωp的正弦波。对解调序列θ1,θ2,…,θn使用四参数正弦波拟合法处理，获得拟合幅度为Δθ、频率为Ωp、直流分量为θc的估计值。则，调制相偏Δθ、调制频率Ωp。以此作为标准值，可校准调制度测量仪的PM解调参数。

3 宽带调制度分析仪的校准

按上述方法，以正弦波滑动拟合实施解调，对测量误差、噪声等具有一定抑制作用，可获得优于其它方法的解调准确度。具体效果还和波形信噪比等因素有关。通常，要求每个载波周波具有几十个以上的采样点才能获得足够理想的解调结果。

通常，已调信号的载波频率范围很宽，从kHz量级到几十GHz。而调制产生的信号频宽多在几百kHz以下。因此，对低频载波的已调信号的调制度测量部分，可用上述方法直接测量校准。

而对于高频载波部分，很难用上述方法直接测量校准。一则对数字示波器的采样率、频带宽度、存储深度均带来巨大压力；二则，即使能够实现直接测量校准，为同时保证每个载波周期至少有几十个以上的采样点，以及获得一个以上调制信号周期的时长，将导致采样点数极为巨大，后续处理及运算需要消耗超长的时间，效率较低。

专门针对各种调制类带限信号的调制解调发展起来的变频技术，是无线电工程里一项成熟的基本技术。其最大特点是，理论和实践均已证明，以上变频和下变频处理的各种已调带限信号，如AM、FM、PM信号，在满足某些基本条件后，变频前后的波形，仅仅是载波频率发生了变化，原理上，各自的调制信号特性并未发生变化。由此，有如图2所示、针对高频载波、已调窄带宽、带限信号波形的计量解决方案。

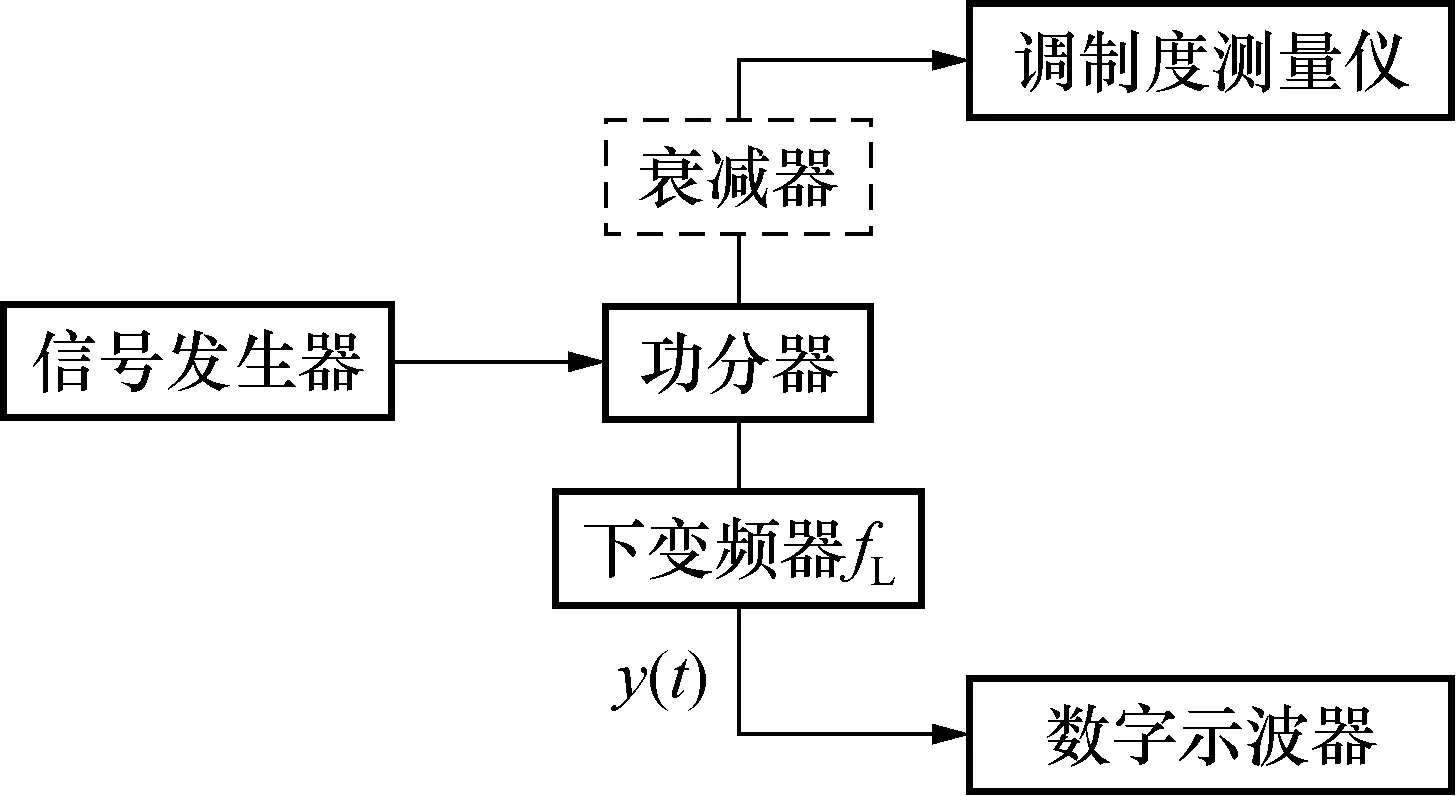
图2 宽频调制度测量仪校准框图Fig.2 The calibration of high frequency modulation meters

如图2所示，信号发生器产生的已调信号通过功率分配器分为两路，一路接到调制度测量仪进行调制度参数分析测量；

另一路通过下变频器，将载波向下移频fL、滤波、放大后，接到数字示波器采集测量。获得数据记录序列为时刻t1,t2,…,tn的采集样本y1,y2,…,yn，采集速率v，采样间隔Δt，ti=i×Δt=i/v，(i=1,…,n)。

3.1 AM信号解调

AM信号下变频测量后，按第2.1节所述获得解调参数，以校准调制度测量仪的AM解调参数。

3.2 FM信号解调

FM信号下变频测量后，按第2.2节所述获得调制频偏Δf、调制频率Ωf；其载波频率为fc+fL。以校准调制度测量仪的FM解调参数。

3.3 PM信号解调

PM信号下变频测量后，按第2.3节所述获得调制相偏Δθ、调制频率Ωp；其载波频率为fc+fL。以校准调制度测量仪的PM解调参数。

4 实验验证

用FSMR-26型测量接收机作为被校准的调制度测量仪，其频率范围为20 Hz～26.5 GHz，幅度量程为-130～10 dBm；其中：

AM信号解调能力：调幅度量程0～100%；误差范围±0.5%～±1.5%；调制频率范围50 Hz～100 kHz；解调失真0.1%。

FM信号解调能力：最大频偏500 kHz；误差范围±1%～±3%；调制频率范围50 Hz～200 kHz；解调失真0.1%。

PM信号解调能力：最大相偏10 krad；误差 ±1%；解调失真0.1%。

用DPO71254B型数字示波器作为标准仪器，其A/D位数8 bit；频带宽度12.5 GHz，最高采样速率50 GSa/s，最大存储深度31兆点。

用E4432C型矢量信号源作为信号发生器，其频率范围为250 kHz～6 GHz，幅度范围为-136～10 dBm；误差范围±0.6～±1.5 dB；其中：

AM信号参数：调制度范围0～100%，分辨力0.1%；调制频率范围0 Hz～10 kHz(宽带调制范围400 Hz～40 MHz)；调制失真<1.5%。

FM信号参数：最大频偏64 MHz，分辨力0.1%；调制频率范围0 Hz～100 kHz(3 dB带宽时0 Hz～10 MHz)；调制失真<1%。

PM信号参数:最大相偏640 rad；误差±0.1%±0.01 rad；调制失真<1%。

4.1 AM信号解调校准

按图1所示接线，信号发生器E4432C输出幅度0.00 dBm、载波频率100 MHz、调幅度30%、调制频率100 kHz的AM信号，经过功分器一分为二，一路直接输入被校准的调制度测量仪FSMR-26，经其分析后获得参数为：

射频幅度-6.550 dBm，载波频率100.000 000 0 MHz；调制频率：100.000 0 kHz，正峰26.708%，负峰-26.735%，调幅度26.722%。

另外一路接入数字示波器DPO71254B，其采样速率为3.125 GSa/s，存储深度125 000点。采集数据如图3所示。

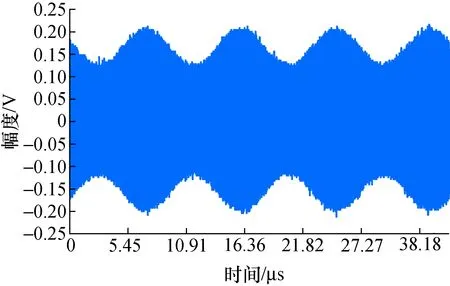
图3 AM信号采集数据波形Fig.3 sampling series of AM signal

按第2.1节所述方法，得解调波形如图4所示。

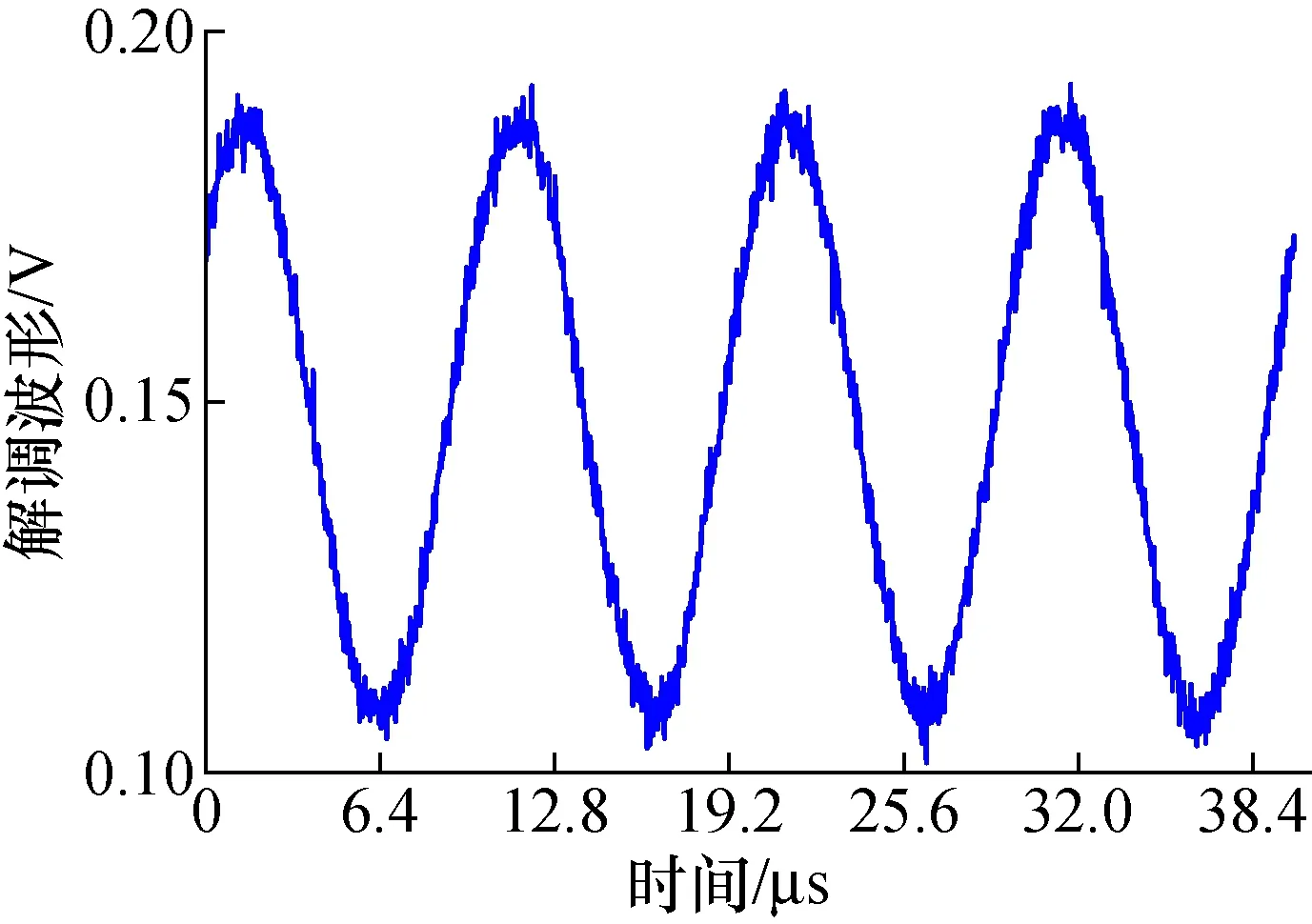
图4 AM信号解调数据波形Fig.4 Demodulation series of AM signal

同时，获得解调幅度为ΔA=39.712 mV，其标准偏差为70.143 μV；调制频率Ωa=100.103 8 kHz，其标准偏差为210.350 Hz；载波幅度C=269.681 mV，其标准偏差为3.147 mV。调幅度为ΔA/C=26.97%，其绝对标准偏差为0.315%。

4.2 FM信号解调校准

按图1所示接线，信号发生器E4432C输出幅度0.00 dBm、载波频率250 kHz、调制频偏25 kHz、调制频率1 kHz的FM信号，经过功分器一分为二，一路直接输入被校准的调制度测量仪FSMR-26，经其分析后获得参数为：

调制频率：999.999 9 Hz，正峰25.02 kHz，负峰-25.01 kHz，调制频偏25.02 kHz。

另外一路接入数字示波器DPO71254B，其采样速率为625 MSa/s，存储深度1250 000点。采集数据局部如图5所示。

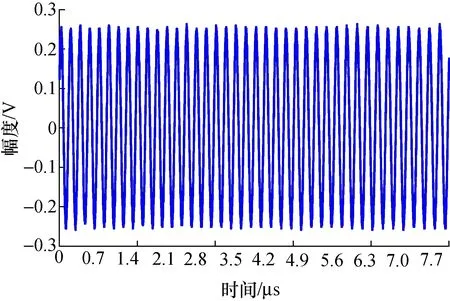
图5 FM信号采集数据波形(局部)Fig.5 Sampling series of FM signal(partial)

按第2.2节所述方法，得解调波形如图6所示。

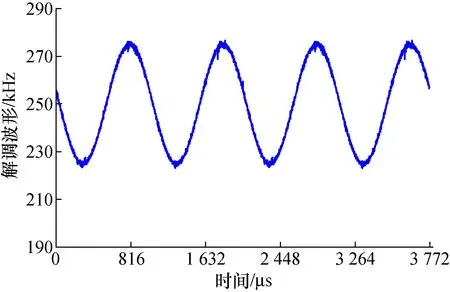
图6 FM信号解调数据波形Fig.6 Demodulation series of FM signal

同时，获得调制频偏Δf=24.996 36 kHz，其标准偏差为21.32 Hz；调制频率Ωf=999.215 3 Hz，其标准偏差为1.432 4 Hz；、载波频率fc=249.649 5 kHz，其标准偏差为433.6 Hz。

4.3 PM信号解调校准

按图1所示，信号发生器E4432C输出幅度0.00 dBm、载波频率250 kHz、调制相偏10 rad、调制频率10 kHz的PM信号，经过功分器一分为二，一路直接输入被校准的调制度测量仪FSMR26，经其分析后获得参数为：

调制频率：10.000 00 kHz，正峰9.968 rad，负峰-10.12 rad，调制相偏10.04 rad。

另外一路接入数字示波器DPO71254B，其采样速率为3.125 GSa/s，存储深度625 000点。采集数据如图7所示。

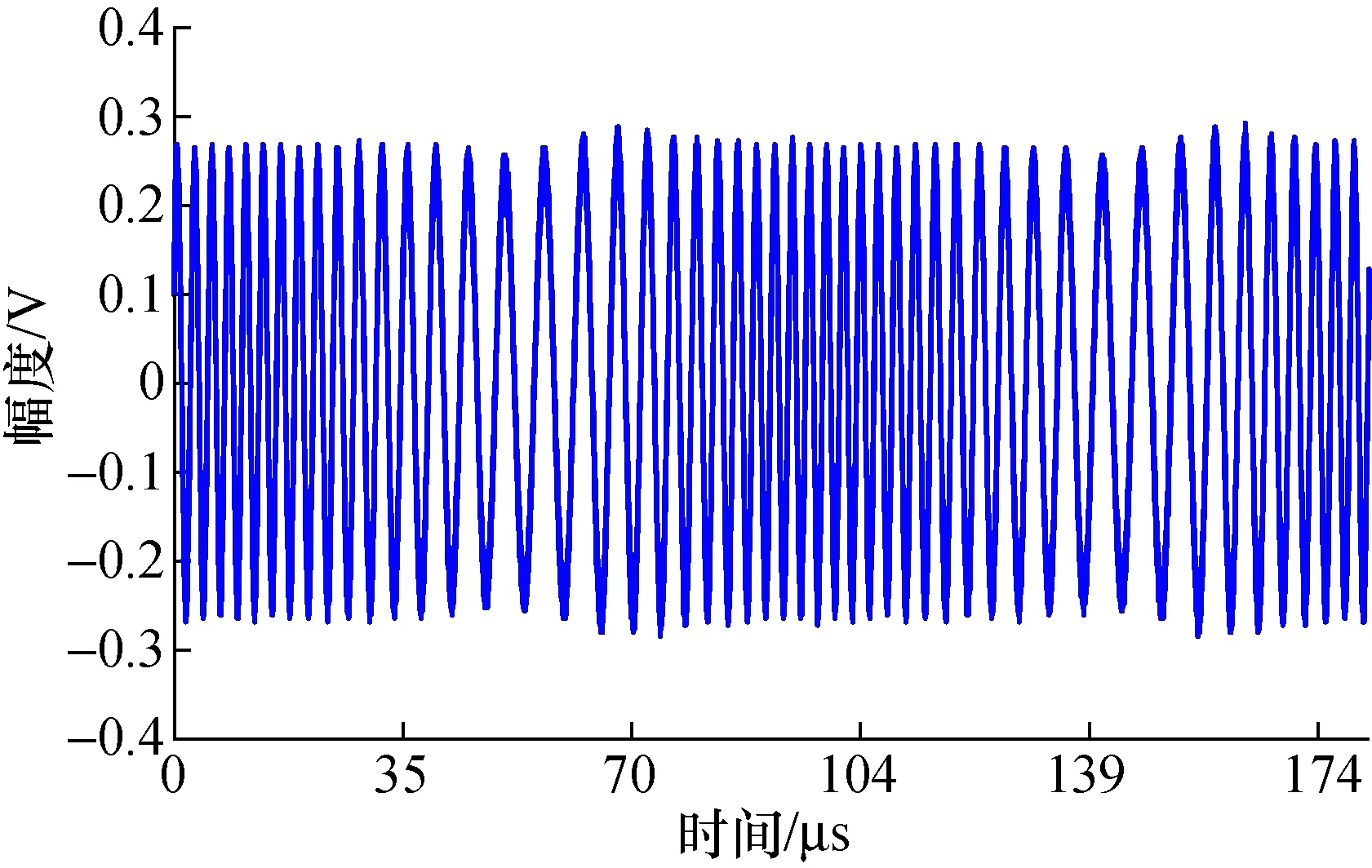
图7 PM信号采集数据波形Fig.7 Sampling series of PM signal

按第2.3节所述方法，得解调波形如图8所示。

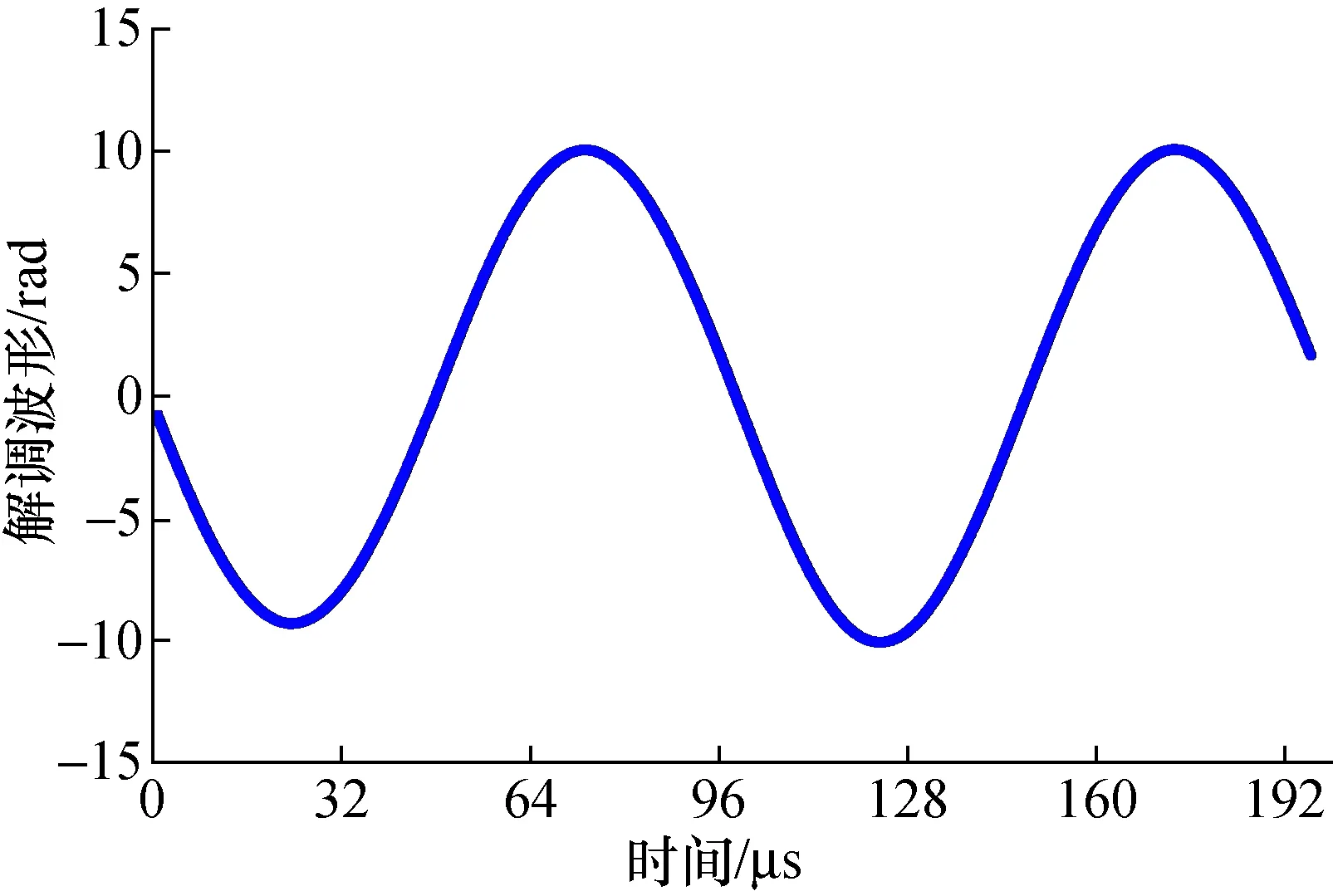
图8 PM信号解调数据波形Fig.8 Demodulation series of PM signal

同时，获得调制相偏Δθ=10.023 874 rad，其标准偏差为0.005 45 rad；调制频率Ωp=10 022.2 Hz，其标准偏差为72.3 Hz。

5 问题讨论

无线电工程中，已有的AM、FM、PM信号均属于高频载波下的窄带调制信号。即调制产生的附加带宽远小于载波频率，调制度测量仪的指标参数具有同样特点，使得正弦拟合法可以用于解调，并且，下变频技术可直接应用于调制域分析中。

对于AM信号波形，人们最为关注的并非其绝对幅度值和绝对频率，而是稳定的载波幅度随调制波形而变化的变化量部分，它相对于载波幅度之比，以及其随时间变化的规律，即幅度调制规律。

对于FM信号波形，人们最关注的也并非其绝对频率和绝对幅度，而是稳定的载波频率随调制波形而变化的变化量部分，以及变化的频率，即频率调制规律。

PM信号波形的状况与FM波形相似。

通常，射频信号的上变频，主要是通过非线性器件的倍频效应，再经滤波放大实现；微波信号的下变频，主要通过非线性器件与本地振荡器的频率进行混频，再滤波放大来实现。

对于高频载波下的窄带调制信号，无论是上变频还是下变频，都能够获得理想的频率平移效果。其主要局限为变频前后信号波形除了频率被平移以外，其变频前后的幅度会有较明显变化。

对于3种已调模拟信号波形而言，其绝对幅度和绝对频率的关注度并不很高。其中，AM信号只关心在窄带范围内，变频器的幅频特性保持恒定即可。对于FM、PM信号，变频器的幅频特性保持恒定的要求还要弱些。现有技术下的变频器，尽管在宽频率范围，其幅频特性不够平坦，但在较窄的频段里，总能选择到幅频特性基本平坦的变频器。实现本文所述的精确解调过程。

本文所述方法中，要使用正弦波模型拟合载波数据，而被调制后的载波，虽然形状上与正弦波相像，但本质上已不是严格意义的正弦波，因此，为保证拟合收敛，不宜用多周期波形段拟合，只能使用1个周波左右或少于1个周波的波形段进行曲线拟合。客观上要求采集测量序列在1个载波周期内有足够多的采样点。通常，每周期少于20个点时不易获得良好的拟合精度，每周期100点以上时可望获得稳定的拟合结果。

实际采集测量获得的波形曲线序列，往往在起始端部分由于噪声干扰、初始相位状态的周期截取等，会产生不收敛问题。使用残周期拟合方法进行初始部分的第1段波形参数估计，将可以获得良好的收敛效果[9]。

正弦拟合法用于调制域分析，是有边缘效应的。很显然，由于需要通过模型方式获得解调参数，所以，最边沿的测量点无法获得良好的解调效果，应予以删除，或近似替代的方式给出边沿附近点的解调结果的估计值。

对于AM信号波形的解调，最终的调制度是调制带来的幅度变化ΔA和未调制时的幅度A之比值。因而，影响AM波形解调误差的因素，除了软件算法以外，数字示波器的影响主要体现在其幅度测量线性关系是否稳定一致上，其线性度是否优良至关重要。在线性度理想的情况下，幅度增益的整体变大或变小，对于本身就是幅度比的调幅度测量结果基本没有影响。

对于FM信号波形的解调，最终的载波频率、调制频偏、调制频率等的计算，均直接依赖于采样速率，因而，采样速率本身的误差，将直接影响FM的解调结果，造成波形参数误差，采样间隔的不均匀，将造成额外的解调波形失真等。幅度测量误差对其影响则处于次要地位。可以认为，FM信号波形的解调参数，直接溯源到数字示波器的采样速率或时基准确度上。

对于PM信号波形的解调，可以认为是按FM信号解调获得的波形的再积分结果。因此，其误差来源与特点有很大一部分与FM信号波形的解调相同，均主要来源于波形采样速率误差和采样间隔的均匀性。另外的部分，则取决于初始相位的定值上。

关于鉴相，需要指明的是，首先，载波信号的相位在均匀采样序列中，是与载波频率有关的逐点线性增加的一条直线，而相位调制信息是叠加在该直线上的叠加波形，在鉴相解调中应该将载波造成的线性趋势剔除掉[8]。另外，其最大的难点是其值域的确定和初始值的选取。若无任何先验知识，很难正确选取它们。对于本文所采用的积分法鉴相来说，尤其如此。最后，需要说明的是，由于积分法的特点，导致每一个瞬时频率测量值的误差都会在积分中被累积。

对这些问题，本文采取的是模型化解决方式。针对PM信号源产生的是周期性振荡信号的特征(多为正弦振荡信号)，对PM波形的调制信号的值域或特征预先有一个粗略的估计。例如，零均值振荡特征，或者正负对称型值域特征(零中值特征)。首先，选取鉴相时的初始值为0 rad.或任意一个固定值，在完成积分鉴相过程之后，按照零均值特征或零中值的正负对称特征进行波形平移，获得最终的解调结果。

目前，宽频调制度测量仪的频率范围，已经与数字示波器的频带宽度相近，对于不能实现以数字示波器直接测量与解调的高频载波的已调信号，直接使用下变频技术，将其移频转换成低载波频率的已调信号，再用数字示波器进行解调分析与处理，将是一种有效的校准方式。但每经过一次变换环节，都将引入额外的误差或不确定度，相应的影响，需要专门研究予以定量评估[10]。

目前的技术条件下，调制度测量仪的幅度测量范围，要宽于数字示波器，主要体现在示波器多用于毫伏级以上的幅度信号波形测量与分析，更微小的信号超出了其测量分辨力的能力范围，而调制度测量仪可以测量分析小得多的信号波形。在计量校准中，可以将较大幅值的信号直接提供给数字示波器，而以衰减器衰减后的微小幅度信号，用以提供给调制度测量仪进行测量分析，以达到用大幅度信号校准小幅度量程的目的。也可以使用放大器对已调信号进行放大后再提供给数字示波器，以达到相同的目的。

由于使用了滑动拟合方式实现解调，导致本文方法所需数据量较大，分析运算花费的时间成本也较大。如何提高效率，减少数据量，有待后续研究解决。

6 结 论

调制度测量仪校准的难度，不在于其指标的高或低，主要是其包含了调制和解调之间的转换环节。任何以硬件技术实现的、以信号为依托的调制与解调过程或环节，其最后关头总要面临同样的难题，即指标最高者很难直接校准溯源。

本文所用的方法，其解调部分是在通用数据采集平台下，以软件算法实现的。而软件算法面向的并非是物理信号的波形，而是数据序列，自然会有理想仿真数据，可以完整表述其特性。包括误差特性、失真特性、延迟特性等。加上通用采集平台已经能够校准溯源，因而可以用于对调制度测量仪进行校准溯源，本文所用方法的实验验证，也恰好证实了这一结论。