基于改进深度信念网络训练的冷轧轧制力预报
魏立新,王 恒,孙 浩,呼子宇
(1.燕山大学 智能控制系统与智能装备教育部工程研究中心,河北 秦皇岛 066004;2.燕山大学 工业计算机控制工程河北省重点实验室,河北 秦皇岛 066004)
1 引 言
在带钢冷轧轧制过程中,轧制力是最重要的工艺参数之一,其设定精度将直接影响带钢穿带的稳定性和减少带头带尾长度[1]。因此,现场应用对轧制力的设定提出了更高的要求。轧制生产过程受到多种因素的共同影响,具有非线性、不确定性等特点[2]。传统数学模型大多依据Bland-Ford-Hill公式对轧制力进行计算,适用范围比较窄,难以满足现场多规格产品柔性化生产的需求[3]。如何高精度的预测板带轧制力,进而提升产品质量已经成为亟待解决的问题。近年来,随着人工智能和深度学习的快速崛起,人工智能模型在自动化领域的应用逐渐增多[4]。Mahdi Bagheripoor等使用三维有限元模拟分析和神经网络相结合的方法来预测轧制力,不但提高了预测精度,而且可以方便的应用到不同带钢尺寸的模型中[5]。陶功明等采用高斯过程回归算法,基于现场生产数据建立了压下量与轧制力模型,为钢轨轧制过程轧制力的精确控制提供了一种残差较小的统计模型[6]。Chen Z M等提出一种基于多重支持向量机(multiple support vector machine,MSVM)的轧制力预测方法,将模型的输入划分为多个子空间,并对每个子空间分别建立SVM模型,最后合成所有子空间的输出来预测轧制力[7]。赵志伟等提出一种使用人工蜂群算法优化反向传播神经网络的初始权值、阈值和网络结构的轧制力预报方法,该方法的轧制力预报精度明显提高[8]。王智等采用粒子群算法(particle swarm optimization,PSO)优化BP网络建立智能模型并与标准BP网络作对比,实验结果表明PSO-BP神经网络的预测精度明显提高,误差率可以控制在10%以内[9]。窦博采用贝叶斯神经网络建模进行轧制力预测,并使用乘法网络对模型进行优化,实验结果表明预测精度相比于加法网络有较大提升[10]。曹卫华等提出一种基于极限学习机(extreme learning machine,ELM)的轧制力预报模型,运用现场采集的数据对模型进行测试,结果证明相比于传统模型,能够快速准确的实现轧制力预测[11]。以上模型所用方法均属于浅层神经网络模型,针对复杂问题其表达能力受到一定制约,难以发现输入信息之间的深层联系。随着轧制数据的累积,计算机性能的增强,深度学习模型的优势日益明显。其中,深度神经网络具有较强特征提取、复杂函数表达及泛化能力[12]。深度信念网络作为深度神经网络的一种,能够将输入信息映射到高维空间,发现并提取数据鲁棒性隐藏特征,对于复杂非线性模型有更强的学习能力[13]。
本文利用深层网络较强的特征学习能力,提出一种基于改进深度信念网络的轧制力预报模型。隐含层加入去噪机制可以对输入训练数据进行预处理,滤除数据中的噪声干扰,提高网络的学习能力。改进对比散度算法对采样梯度进行修正,使得网络进行参数更新迭代时都能最大程度的趋向于真实梯度,加快网络的训练速度。
2 深度神经网络
深度神经网络作为机器学习的最新研究成果,具有浅层网络无可比拟的优势。冷连轧过程存在外部环境干扰会产生噪声数据,为了滤除噪声,在标准受限玻尔兹曼机(restricted Boltzmann machines,RBM)基础上引入去噪机制构建深度网络模型,克服标准RBM网络对噪声处理差的缺陷,提升轧制力预测精度。
2.1 受限玻尔兹曼机
受限玻尔兹曼机是一种包含可视层和隐含层的马尔科夫随机神经网络概率图模型[14]。其网络拓扑结构如图1所示。网络下层为可视层,由神经元vi组成,用于训练数据的输入。网络上层为隐含层,由神经元hj组成,作用为特征提取器,可以学习到输入训练数据的关联特征。ai为输入神经元的偏置向量,bi为隐含层神经元的偏置向量。
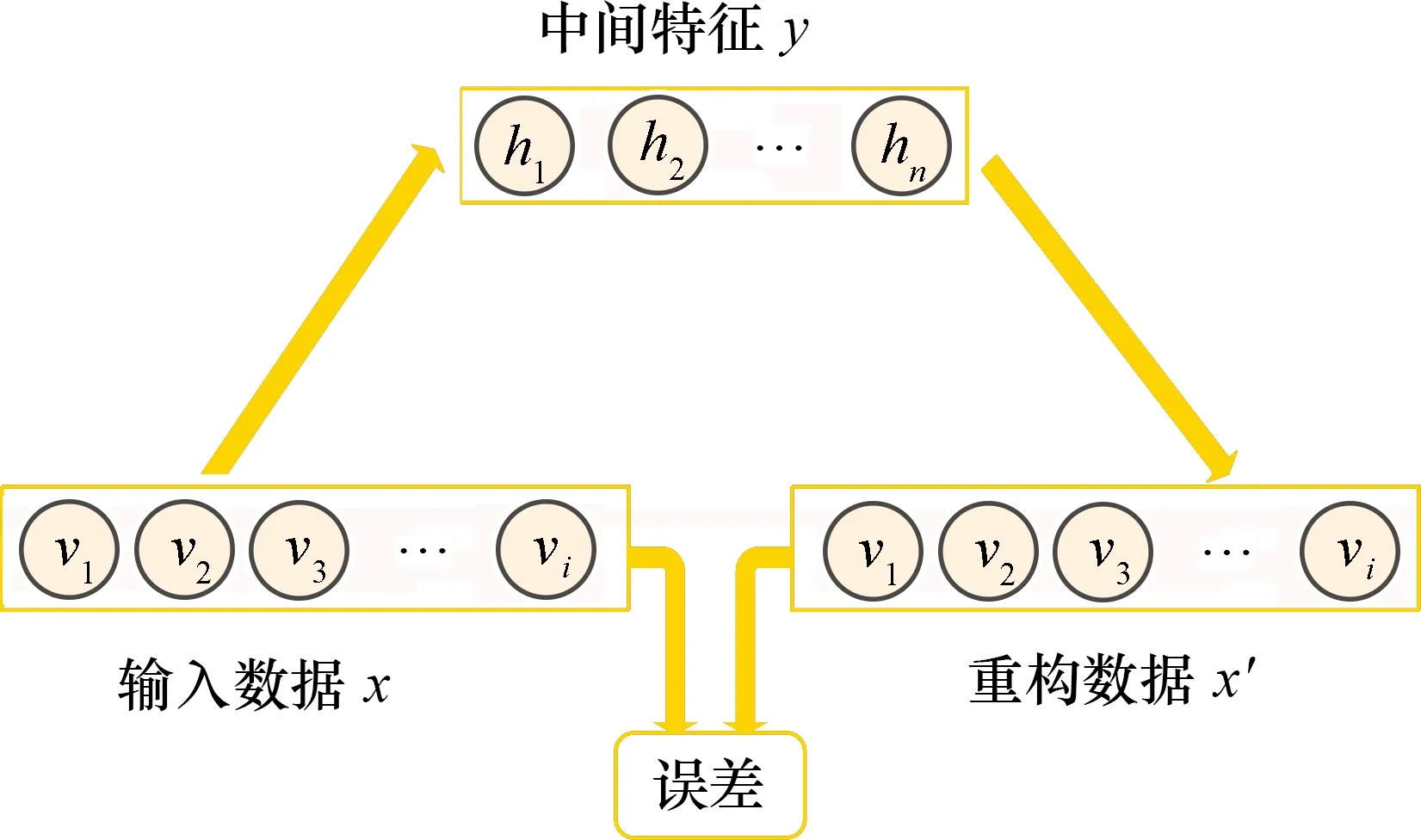
图1 RBM网络拓扑结构图Fig.1 Network topology diagram of RBM
为了保证可视层与隐含层之间的条件独立性,RBM网络具有层内无连接,层间全连接的特点。本文将二值受限玻尔兹曼机作为研究对象,随机变量(V,H)的取值范围是(v,h)∈(0,1)。在描述RBM网络时引入能量函数[15],能量函数定义:
(1)
式中:wj,i为输入神经元i和隐层神经元j之间的连接权重向量。网络模型参数为θ={wj,i,ai,bj}。基于能量函数,状态(v,h)的联合概率分布为:
(2)
式中Zθ为配分函数,Zθ=∑v,he-Eθ(v,h)。
由联合概率分布可以得到边缘概率分布:
(3)

(4)
当给定一组输入数据时,隐含层第j个激活单元概率为:
P(hj=1|v)=
(5)
相应的,当隐含层数据确定后,输入层神经元的取值概率为:
(6)
式中:σ(x)为Relu激活函数,可以将输入数据x映射到0~1之间。
RBM网络训练的目的是使得网络学习到的数据特征分布尽可能的与原始输入数据的特征分布相同,但是由于配分函数的存在,联合概率分布函数Pθ(v,h)求解较为复杂。基于对比散度算法的吉布斯抽样可以解决这一问题。
2.2 去噪受限玻尔兹曼机模型建立
标准受限玻尔兹曼机模型在训练样本数据时,由于数据中包含背景噪声,导致网络隐含层学习到的数据分布特征不能匹配原始数据固有特征,因此会导致网络学习性能下降,影响最终预测结果。
因此,在标准受限波尔兹曼机网络模型的基础上,将去噪机制加入到隐层神经元中,建立去噪受限玻尔兹曼机模型。对比标准RBM网络模型,去噪受限玻尔兹曼机网络模型将隐含层分为两组。在网络迭代训练期间,目标特征出现的频率高于背景噪声,因此其对应的隐层神经元被激活的次数更多,并且激活值更大[16]。根据此特点,对隐层神经元进行分组。给定分组阈值函数为:
(7)
式中:fi(x)为隐层第i个神经元的活跃度;K为隐层神经元的个数;θi为隐层第i个神经元的输出值。
隐层分组依据:将整体隐层输出看作单位“1”,当某个隐层神经元的活跃度大于阈值函数设定值后(0.8),将该神经元看作是数据特征提取单元,否则看作是噪声背景单元。之后,在每次吉布斯采样迭代算法过程中,逐渐降低噪声背景单元的权重,以减小噪声对数据特征提取的干扰。
为了获得高精度的预测结果,本文将多个去噪受限波尔兹曼机进行叠加组成深度信念网络。网络结构示意图如图2所示。

图2 深度网络整体结构图Fig.2 Deep network overall structure
定义网络重构代价函数:
(8)

(9)
式中:第1项为均方差项,可以使重构误差达到最小;第2项为权重衰减项;λ为权重衰减系数,其目的可以减小权重幅度,防止过度拟合;m为样本数据个数;v为输入层节点数目;h为隐层节点数目。RBM网络训练精度越高,隐层对输入层的重构误差越小,即网络的重构代价函数越小。
3 网络训练算法
网络训练标准算法为对比散度(contrastive divergence,CD)算法,以吉布斯采样为基础,通过多步吉布斯采样来获得一定精度的目标采样,进而获得最终的目标梯度近似值。RBM训练的目的是通过调节网络权值,让隐层节点状态值最大程度的重构输入层节点的状态值,此时,RBM可以用来表示输入数据的分布特征。算法本质上是通过吉布斯采样迭代获得的采样梯度来近似估算似然函数的真实梯度。由于采样迭代次数有限,用于梯度计算的样本与实际分布的样本之间存在差异,包括数值误差和方向误差,从而导致网络无法收敛到精确值[17]。针对此问题,在对梯度误差进行分析的基础上,建立梯度修正模型,同时对采样梯度的大小和方向进行修正,并将其应用到CD算法上,重新定义RBM网络训练代价函数:
(10)
式中:第1项为重构误差代价函数的负值,函数值越小,对应负值越大;第2项为样本数据分布的对数似然函数,基于对数最大似然估计方法,RBM网络训练的目的就是求得使似然函数达到最大的参数值。本文用该代价梯度作为梯度修正项来修正由采样算法求得的近似梯度,这样就极大的提高了梯度方向计算时的正确性。由于该采样算法可以以较快的速度逼近待求参数收敛区域,所以能够加快网络训练。网络训练伪代码如表1所示。

表1 算法流程伪代码Tab.1 Algorithm flow pseudo code
表1中:
Δwij=η[P(h(0)=1|v(0))v(0)T-P(h(1)=
1|v(1)T)]
(11)
Δai=η[v(0)-v(1))]
(12)
Δbj=η[P(h(0)=1|v(0))-P(h(1)=1|v(1))]
(13)
4 轧制力预报
4.1 数据集及模型输入的确定
以某钢厂1 200 mm四辊五机架冷连轧生产线第4机架轧制过程中9 000条轧制数据作为实验数据集,钢种为St16。取其中8 000条数据用作网络训练,1 000条数据用作网络测试。深度网络训练集分为80个batch块,batch-size=100。每次随机选取一个batch块进行训练,直到所有数据训练完毕。数据选取范围如表2所示。

表2 输入数据及网络参数Tab.2 Input data and network parameters
传统轧制力预报采用数学机理建模[18]方法,即基于Bland-Ford-Hill公式的简化式进行建模:
(14)

(15)
式中:μ为摩擦系数;ε为压下率,ε=(h0-h1)/h0;R′为轧辊压扁后的辊径。摩擦系数μ随着轧制生产环境的变化而不断变化,且易受带材速度的影响,无法用公式精确计算得到。因此在用神经网络建模时,不将其作为输入节点,而是利用网络的自适应性将其包含在网络的内部[19]。综合考虑影响轧制力预测精度的各种因素,最终选取板带宽度B,初始厚度H,入口厚度h0,出口厚度h1,入口张力τf,出口张力τb,轧辊半径R,出口带材线速度v这8个变量作为模型输入,轧制力P作为模型输出。本文采用深度信念网络方法进行建模。深度信念网络用来提取输入数据的隐含高维特征,然后将其传递给回归器进行预测,可以学习到输入数据的特征分布,在一定程度上提高了预报精度。
4.2 仿真结果分析
为了提高预测精度,将多个去噪受限玻尔兹曼机进行叠加组成深度信念网络,但随着网络层数的加深,过拟合现象的问题也会出现。同时,预测精度跟训练周期也存在较大的关联。预测精度、网络层数、训练周期三者的关系如图3所示。

图3 不同网络层数、训练周期和预测正确率的关系图Fig.3 Relationship diagram between different network layers,training period and prediction accuracy rate
由图3可以看出,当迭代次数固定时,网络层数从一层增加到四层,预测结果正确率显著提高,当网络层数继续增加时,正确率出现下降的趋势;当网络层数固定时,随着训练周期的增加,预测正确率呈现上升趋势。综合考虑三者关系,当网络层数为4层,迭代次数为320时,正确率最高。因此,设置网络层数为4层,迭代次数为320。网络输入层为影响轧制力的8个变量。隐含层节点数目与预测正确率关系如图4所示。从图4可以看出,当节点数目为32时,正确率达到最高,所以各隐含层神经元数量设定为32个,即网络结构为8-32-32-32-32-1。

图4 不同隐含层节点个数与预测正确率关系图Fig.4 Relationship between number of nodes in different hidden layers and prediction accuracy rate
在网络训练过程中,首先使用标准CD算法进行训练,训练步骤如文中第2节所述。然后在标准CD算法基础上,建立梯度修正模型,使得梯度下降方向最大程度的拟合真实梯度,加快网络收敛速度。标准CD 算法以及对其改进后,误差与迭代次数关系如图5所示。
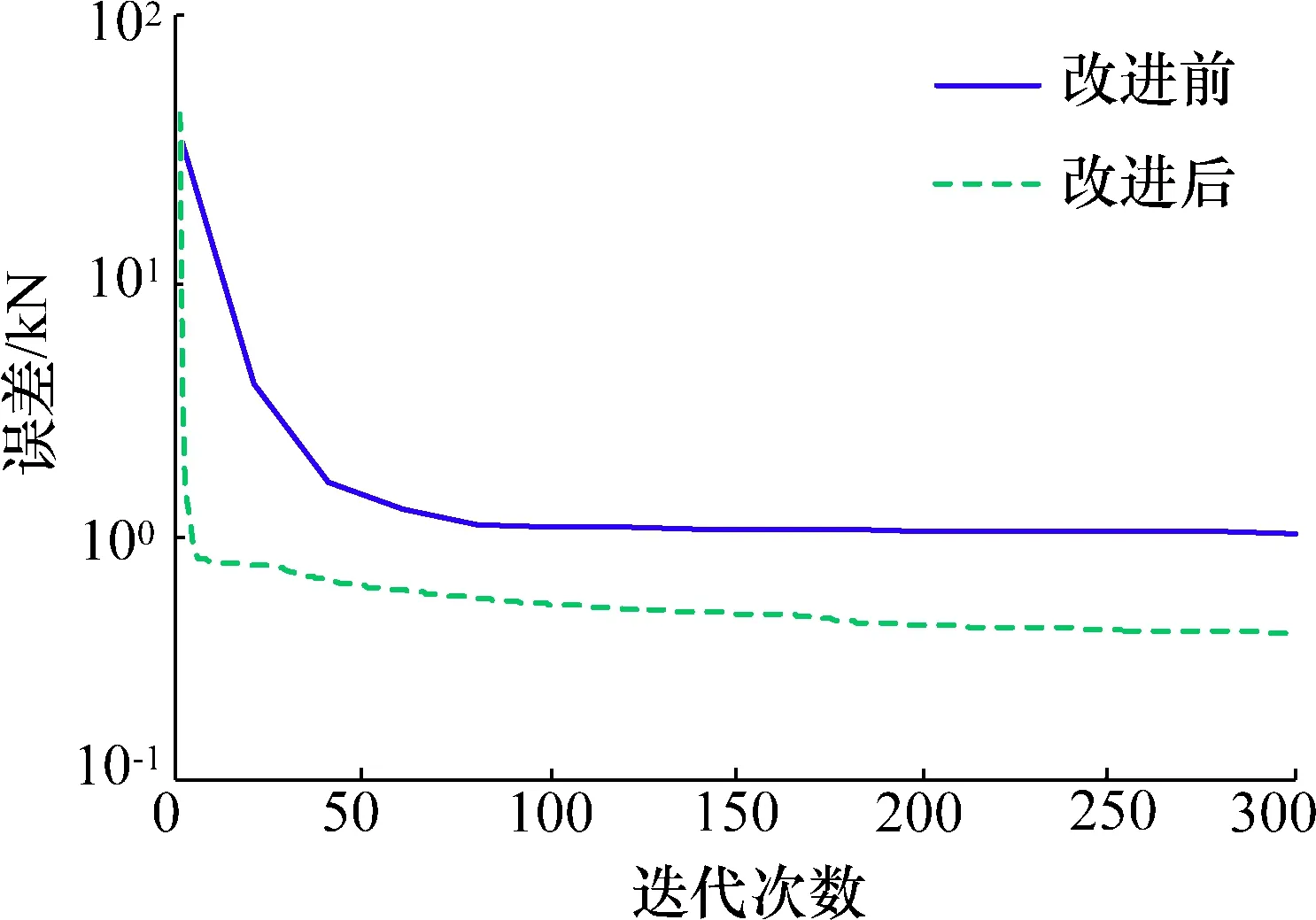
图5 不同算法对比图Fig.5 Comparison of different algorithms
由图5可以看出,在迭代次数相同的情况下,加入梯度修正模型后的CD算法在训练初期可以加快网络的收敛速度,缩短训练时间。
为了将数据中的噪声去除,将去噪机制加入到网络训练过程中,以此来提高网络学习能力。图6为加入去噪机制前与加入去噪机制后的轧制力预测结果对比图,图6中2条实线为±5%误差线,可以看出,去噪模型的预测效果更加优异,有更多的结果落在5%误差带以内。
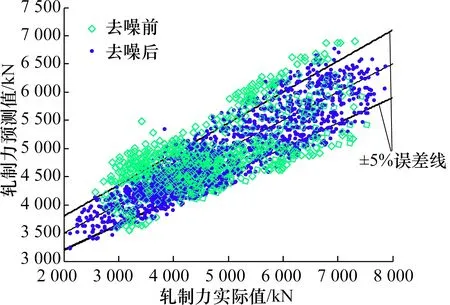
图6 预测结果对比图Fig.6 Forecast result comparison chart
图7为2种网络模型对轧制力预测的预测值和真实值的拟合曲线。从图7可以看出,去噪受限玻尔兹曼机可以较为准确地实现轧制力的预测,满足实际生产需求。

图7 不同模型轧制力预测值与真实值的拟合曲线Fig.7 Fitting curves of the predicted value of rolling force and the true value of different models
图8为不同网络层数、迭代次数与相对误差的关系图,由图可以看出,在网络层数固定的情况下,相对误差会随着迭代次数的增多而不断下降。当迭代次数固定时,相对误差值会随着网络层数的加深先降低然后升高,且网络层数为4层时达到最小值,相对误差大小为4.32%。
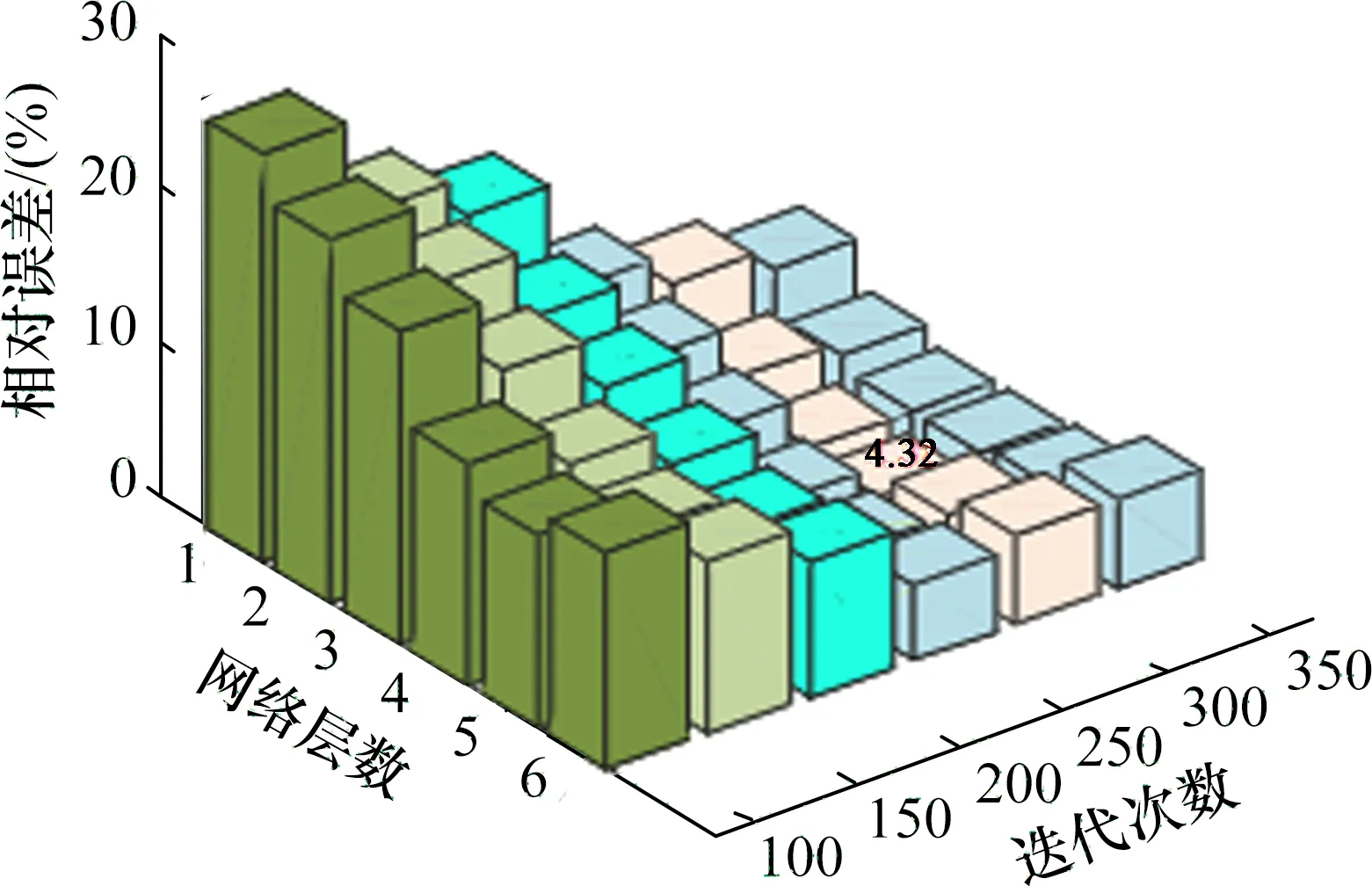
图8 不同网络层数、迭代次数与相对误差的关系图Fig.8 Relationship between different network layers,iterations and relative error
表3为不同模型各种参数的对比结果。由表3可以看出:1)极限学习机(单隐层神经网络)由于随机生成输入权重向量以及隐层偏置向量,因此具有较快的建模速度,但浅层网络对数据的学习能力欠佳,预测结果有待提高;2)栈式自编码网络较极限学习机具有更高的预测精度,但是建模时间较长;3)多层感知器[20]未使用深度学习算法,模型出现梯度弥散现象,未收敛;4)本文提出的改进深度信念网络相比于浅层神经网络,预测精度有很大提高,相比于栈式自编码,建模所需时间缩短。
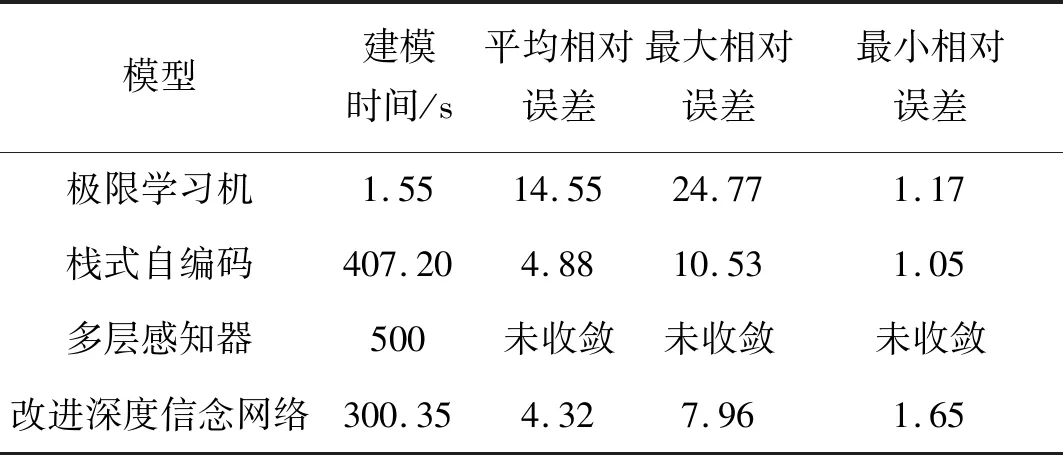
表3 不同模型各项参数对比图Tab.3 Comparison of various parameters of different models (%)
5 结 论
1)本文使用多隐层深度信念网络建立轧制力预测模型,解决单隐层网络预测精度低的问题。针对深度网络会陷入过拟合的固有缺陷,分析了网络层数与相对误差之间的关系,以确定最优的网络结构。
2)针对训练数据存在的噪声干扰,在网络的隐层中引入去噪机制,对输入数据进行预处理,提高网络的学习能力。同时使用改进CD算法对网络进行训练,可以加快网络的收敛速度。
3)实验结果表明,该模型较浅层网络可以提高轧制力预测精度,并在一定程度上缩短了建模时间。

