基于高维随机矩阵综合特征指标的滚动轴承状态异常检测算法
朱文昌,李 伟,倪广县,王 恒
(1.南通大学机械工程学院,江苏南通 226019;2.南通振华重型装备制造有限公司南通分公司,江苏南通 226010)
0 引言
滚动轴承是旋转机械中应用广泛的关键零部件,一旦发生故障,可能给机械设备造成严重的损失[1-2]。因此,有效监测服役滚动轴承的运行状态,及时发现其早期异常状态,保障机械设备安全运行具有重要的研究意义。
文献[3]考虑到轴承自身的运行状态,在状态特征变量确定的空间内,提出一种基于支持矢量数据描述(support vector data description,SVDD)的滚动轴承安全域建模方法用于轴承异常检测,在保证分类准确率的基础上显著提高安全域模型的优化效率。文献[4]研究了基于熵的12个特征对轴承故障检测性能的影响,使用Shannon熵、Renyi熵和Jensen-Renyi发散3种不同的熵测度作为检测熵特征变化的指标,针对轴承早期异常检测提出一种非参数检测方法。尹爱军等通过同步抽取变换对滚动轴承振动信号进行时频分析以获得能量更加集中的时频图,利用复小波结构相似性把时频图的评估值作为滚动轴承性能退化指标,可有效刻画轴承的退化过程,提高对早期微弱故障的敏感程度[5]。文献[6]利用奇异值分解(singular value decomposition,SVD)消除噪声并增强脉冲特性,通过局部均值分解(local mean decomposition,LMD)将纯化的信号分解为一系列故障信息的乘积函数,并对其主要的瞬时振幅进行频谱分析,提取轴承的特征频率进行故障检测。上述方法适合监测数据较小的情况,在样本量较大时存在效率低、计算量较大等问题。
随机矩阵理论是在量子物理领域研究中逐渐兴起的,经过不断研究发展出了大维随机矩阵极限谱分析理论。19 世纪50 年代后,高斯矩阵的半圆律和M-P(Marcenko-Pastur)律相继提出,用于研究大样本协方差矩阵的极限谱分布,随机矩阵理论在量子物理、电网配电、频谱感知等领域得到广泛应用[7]。文献[8]提出了一种使用非线性测量的EOT/GTT随机矩阵方法应用于噪声信号的雷达和声呐追踪,利用随机矩阵特征值进行声音信号区分。文献[9]将随机矩阵集合应用于刚体和结构动力学,通过张量分解产生平行分量和正交分量,测量2个分量相对于标称矩阵的偏差,实现对不确定性的建模。针对国家电网公司采集的用电大数据,文献[10]提出了一种基于高维随机矩阵协方差矩阵特征值的频谱分布,来识别异常功耗状态。对于缺少历史数据的情况,文献[11]提出了负荷随机矩阵(load random matrix,LRM)的负荷相似度计算方法,通过计算预测随机矩阵与历史负荷随机矩阵之间的负荷相似度,可以找到与预测负荷最匹配的历史无功优化调度方案用于无功控制。上述研究都是采用随机矩阵的特征值进行研究,没有考虑特征向量,未能充分挖掘数据信息,丢失了特征向量中包含的有用信息。
针对上述不足,在前期研究基础上,提出一种新的随机矩阵特征值与特征向量相结合的滚动轴承异常检测算法,给出综合特征检测指标的计算方法,研究表明了该算法的有效性及可行性。
1 基于随机矩阵综合特征指标的滚动轴承状态异常检测算法
1.1 监测数据协方差随机矩阵构造
根据滚动轴承健康监测特点,采用大数据分析架构对其进行处理。设监测特征维数为N、监测时间为T、监测节点数为M,在采样时刻ti,设备第j个节点(如测点)所监测的第n个运行状态特征量定义为监测数据子空间:xjn(ti) (i=1,2,…,T;j=1,2,…,M;n=1,2,…,N)。
对节点j而言,监测的所有N个特征量可以构成一个列向量,即:
xj(ti)=[xj1,xj2,…,xjN]T
(1)
将不同采样时刻的监测数据按照时间顺序排列,构成一个时间序列矩阵,即:
X=[xj(t1),xj(t2),…,xj(ti),…] (j=1,2,…,M)
(2)
该矩阵为滚动轴承监测数据矩阵X。
为了对特定时刻、特定节点的数据进行实时分析,采用时间窗方法对时间区间和空间区域参数进行设定,在监测矩阵X中锁定轴承特定时空断面的数据信息。设时间窗口的规模为N×W,则在采样时刻ti,对节点j构成矩阵为
Xj(ti)=[xj(ti-W+1),xj(ti-W+2),…,xj(ti)]
(i=1,2,…,K,j=1,2,…,M)
(3)
采样时刻ti时,窗口数据矩阵构造如图1所示。

图1 窗口数据矩阵构造过程
对窗口矩阵数据进行时域、频域以及时频域等多域特征提取,设取时域特征数为m1、频域特征数为m2、时频域特征数为m3,则提取特征维数为m=m1+m2+m3,构成采样特征矩阵Z∈Rm×W。

(4)

构成高维特征矩阵:
(5)

利用随机矩阵Z′构造出协方差矩阵RZ′(L),用于1.2节特征值及特征向量提取。
1.2 协方差矩阵分解
根据随机矩阵谱分析理论,样本协方差矩阵与总体协方差矩阵谱结构存在定量关系,当样本维数相对于样本量成比例趋于无穷时,在适当的条件下,RZ′(L)的经验谱将收敛于一个确定的分布[12-13]。
对RZ′进行特征分解,可以得到主特征向量:
RZ′(L)=VΛVT
(6)
式中:Λ为RZ′(L)特征值构成的对角阵;V为正交矩阵,其列是对应于不同特征值的特征向量,最大特征值对应的特征向量为v1,v1表示信号的最大特征分量[14]。
1.3 滚动轴承异常状态检测综合特征指标
滚动轴承异常状态检测模型通常将其运行状态划分为正常和异常2种模式,H代表正常状态(health state),A代表异常状态(anomaly state),利用式(6)分别对状态H与状态A所对应的监测数据协方差矩阵进行分解,可以获得2种状态下的特征值与主特征向量。
采用协方差矩阵最大特征值与最小特征值之比D=λmax/λmin作为检验指标,并通过设置合适的阈值,来检测滚动轴承的异常状态。根据随机矩阵谱分析理论的M-P律,求得λmax和λmin的渐进值为b和a,阈值设定为[15]
(7)
但是,特征值只是表征了协方差矩阵的能量信息,特征向量也反映协方差矩阵的部分信息,它包含了滚动轴承监测数据不同时间尺度的局部特征,并且位于特征空间不同投影方向,所以理论上,主特征向量也可以用作早期异常状态检测。创建不同规模的随机矩阵,取c为0.2、0.3、0.4到0.9等不同值,计算最大特征值与最小特征值之比、主特征向量的模,分别如图2、图3所示。由图3可知,与特征极值之比的变化相比,主特征向量的模变化较小、区分度不大。

图2 c不同时最大特征值与最小特征值之比
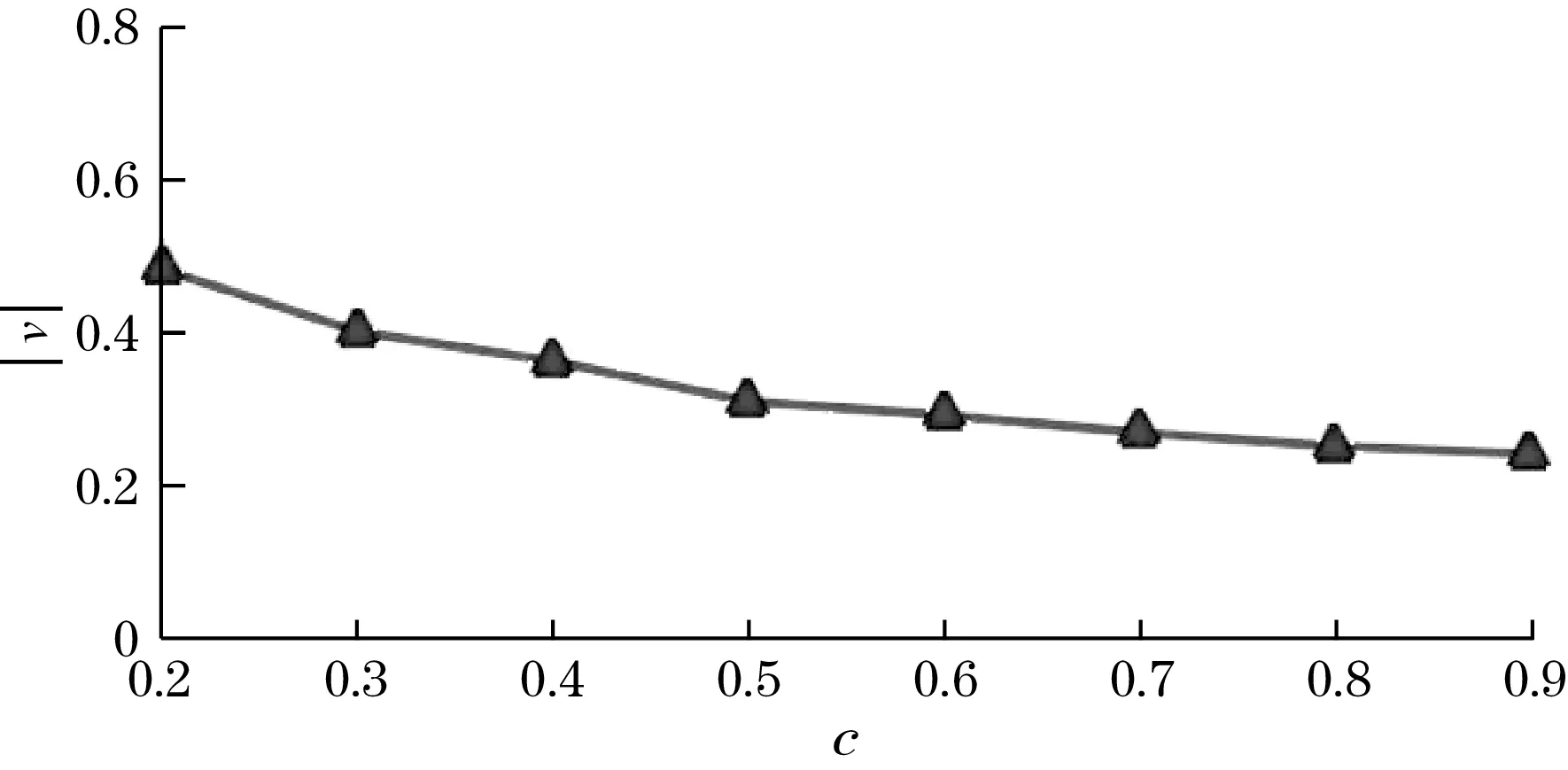
图3 c不同时主特征向量的模
因此,为了充分挖掘协方差矩阵包含的有用信息,综合利用特征值和主特征向量,提出以最大特征值与最小特征值之比D作为主特征向量的放大系数,并结合主特征向量的模,构造一种新的轴承状态异常检测综合特征指标D′,如式(8)所示。
(8)
式中v1为运行轴承监测数据样本协方差矩阵的主特征向量。
综合特征检测阈值为
(9)
式中vH为轴承正常状态监测矩阵所对应的主特征向量。
则滚动轴承异常状态检测判决依据如式(10)所示:
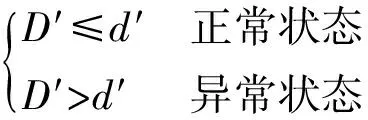
(10)
综上所述,滚动轴承监测矩阵特征值与特征向量共同反映其运行状态,通过最大特征值与最小特征值之比和主特征向量有机融合构成的综合特征值指标,能够更加充分挖掘监测数据信息,从而更全面反映其运行状态,通过与综合特征指标阈值的比较,判定滚动轴承运行状态,从而为设备故障预警和维护提供参考。
基于随机矩阵综合特征指标的滚动轴承异常状态检测算法流程如图4所示。

图4 基于随机矩阵综合特征指标的滚动轴承异常状态检测算法流程图
2 应用研究
滚动轴承试验数据来自于美国航空航天局(NASA)网站,由辛辛那提大学智能维护系统(intelligent maintenance system,IMS)中心完成。4个型号为 ZA-2115 双列滚子轴承布置在同一主轴上,电机转速为2 000 r/min。通过弹簧机构向轴承施加2 722 kg的径向载荷,试验装置每10 min进行一次数据采集,采样频率20 kHz,试验进行到164 h时轴承1出现严重故障认定为失效,共采集984组数据。本文采用轴承1的全寿命振动数据进行分析研究。
2.1 滚动轴承监测随机矩阵构造
根据全寿命数据可得监测数据子空间为xj(ti)=[xj1,xj2,…,xj984]T,采样频率为20 kHz,根据式(2)构造出监测数据矩阵X20480×984。按照式(3)所述时间窗技术对矩阵X进行时空断面数据锁定,对锁定区域数据进行多域特征提取,共提取时域特征30个,即m=30,通过扩充得到采样特征矩阵Z′,L=400,M=500,则c=400/500=0.8。将Z′按照式(4)、式(5)进行数据扩充处理后可以得到高维协方差矩阵,并对其按照式(6)进行特征值分解,得到协方差矩阵最大特征值、最小特征值和主特征向量等相关特征。协方差矩阵的主特征向量变化如图5所示。

图5 协方差矩阵的主特征向量变化曲线
如图5所示,主特征向量变化不明显、区分度小,难以表征和描述滚动轴承正常与异常运行状态之间的差异,因此,采用本文所提出的综合特征指标对主特征向量进行修正。
2.2 滚动轴承异常状态检测结果
利用式(7)~式(9)分别计算滚动轴承状态异常检测特征指标和检测阈值,基于特征值指标和综合特征指标的异常状态检测结果如图6~图8所示。

图6 基于特征值指标的异常状态检测结果
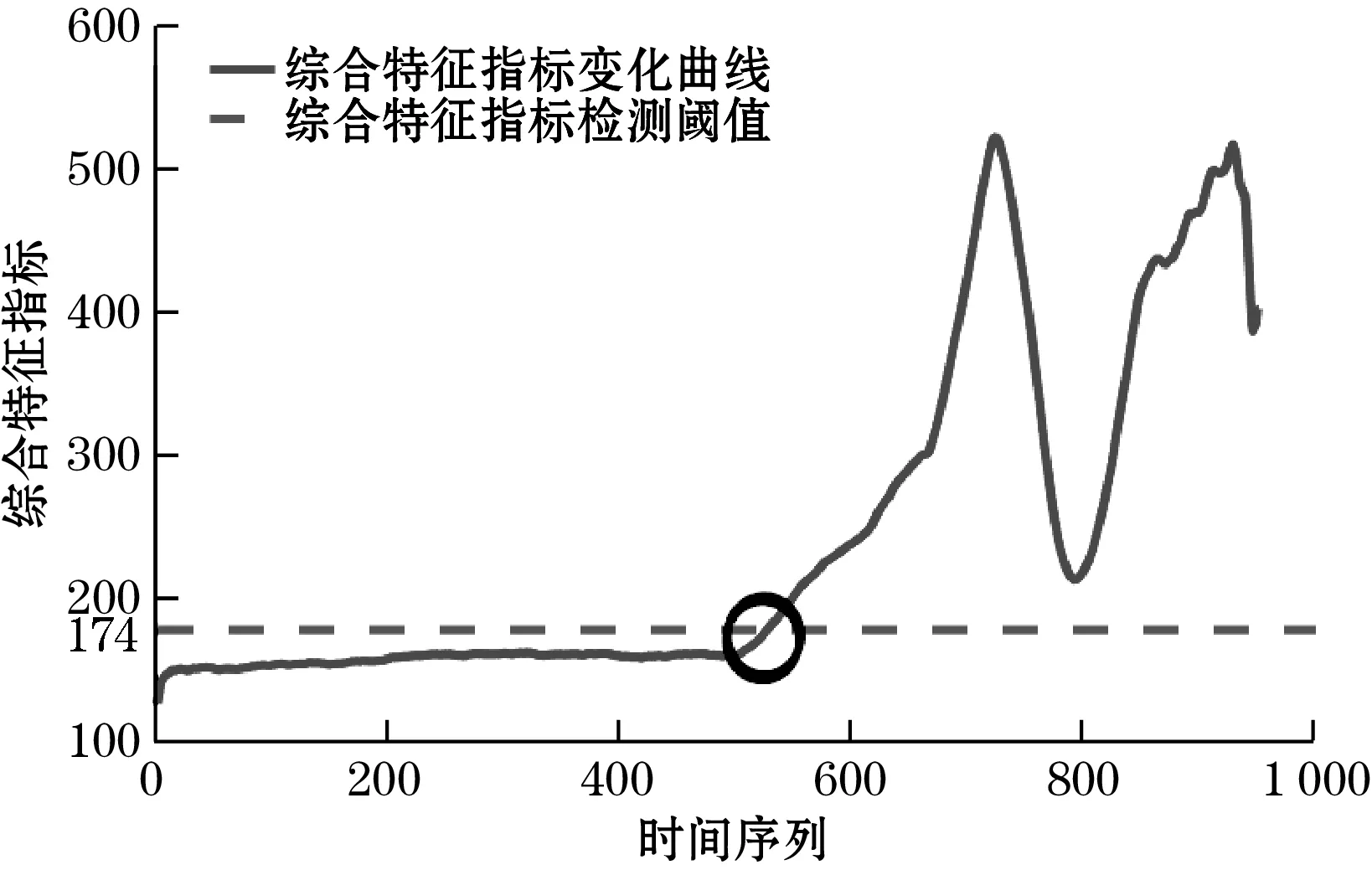
图7 基于综合特征指标的异常状态检测结果
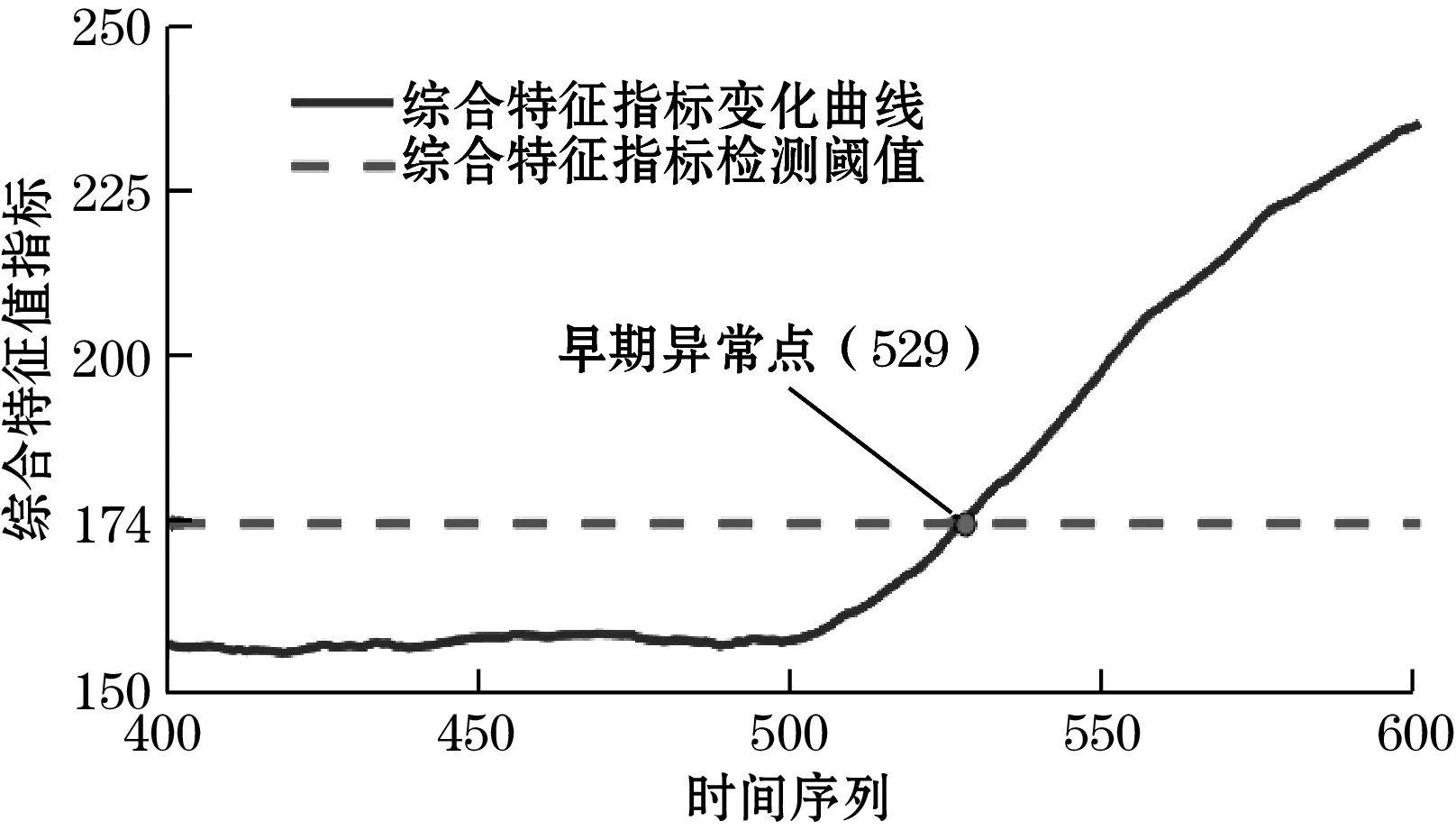
图8 异常状态检测曲线局部放大图
由图6~图8可知,基于最大特征值与最小特征值之比的特征指标检测出的早期异常点为文件序列号595,基于特征值和特征向量融合的综合指标检测出的早期异常点为序列号529,比采用单一的特征指标算法检测时间提前。
2.3 异常检测算法对比
综合指标与特征值指标、峭度指标检测结果对比如图9所示。检测出的轴承1早期异常点对应运行时间如表1所示。

图9 不同算法的滚动轴承异常状态检测结果对比

表1 滚动轴承早期异常点时间 h
如图9所示,基于传统的峭度指标法检测的早期异常点为文件序列号650,综合表1可见,针对全寿命试验中的轴承1,综合特征指标法比单一特征值指标法提前11 h检测出早期异常状态,较传统峭度指标法,能提前约20 h检测出早期异常点,检测时间显著提前。作为正常状态与异常状态的转折,及早检测出异常点意味着能尽早对设备进行故障诊断和预警,对于设备维护保养、保障安全运行、减少事故发生都具有重要的作用。
3 结论
(1)根据滚动轴承健康监测数据特点,利用时间窗技术确定特定时间段监测数据子空间状态特征量,对其进行特征提取构造采样特征矩阵。
(2)为发挥随机矩阵针对高维数据进行处理的优势,利用模拟数据矩阵对特征矩阵进行规模扩充,以达到构建高维随机矩阵的目的。
(3)基于随机矩阵谱理论,对协方差矩阵最大特征值与最小特征值之比的特征值检测指标进行改进,提出融合特征值与主特征向量的综合特征指标,与峭度指标算法和单一特征值指标算法相比,综合特征指标能够最早检测出滚动轴承早期异常点,为故障预警和设备维护提供参考。

