基于平面波分解的封闭空间次级声源布局优化

胥健, 陈克安, 王磊, 张亚洲

1.西北工业大学 航海学院, 陕西 西安 710072; 2.西安艾科特声学科技有限公司, 陕西 西安 710068

有源噪声控制(active noise control,ANC)是基于声波相消性干涉原理的低频降噪技术。影响ANC系统降噪性能的因素很多，除控制算法之外，次级声源布局(个数和空间位置)是另一决定性因素[1]。目前在实际工作中，次级声源布局问题基本上通过大量的现场调试解决，相关工作效率极低，导致研制周期变长，严重阻碍了ANC技术的推广应用。

选择次级声源布局的难点在于存在大量备选位置。解决该问题的一般方法是将其看作组合优化问题，即从所有可能的布局中选择性能最优(降噪量大、鲁棒性好)的方案，人们通常采用遗传算法、模拟退火(simulated annealing，SA)算法等所谓自然算法[2]进行搜索。由于次级声源和误差传感器之间的声传递阻抗(acoustic transfer impedance，ATI)矩阵包含了布局信息，可以通过构造ATI矩阵来进行布局优化。例如Asano等[3]以ATI向量线性独立为目标，利用Gram-Schmidt正交化(GSO)方法逐个选择次级声源。Khalilian等[4]通过奇异值分解先设计“理想ATI矩阵”，再逐个选择次级声源使得ATI矩阵逼近该理想矩阵。声场再现研究中还引入了稀疏正则化方法，通过求解稀疏线性回归问题选择扬声器位置[5-6]。此外，研究者们还提出了许多其他方法，如子集选择方法[7]、约束匹配追踪[4,8]等。

目前的次级声源布局优化方法往往只关注离散点的降噪需求，空间区域降噪效果可能不理想；此外需要预先确定误差传感器的位置，这导致次级声源与误差传感器的布局在某种意义上相互耦合，难以获得最优布局结果。耦合问题可以采用联合优化方法解决[9-10]。Martin和Roure[11]提供了另一种思路，针对自由空间声辐射控制问题，首先利用球谐函数展开将初级声场解析表达，通过球谐函数和多极子源之间的对应关系确定次级声源布局，然后应用遗传算法优化误差传感器布局，这样将二者的优化分离开来。类似地，文献[12]中对于二维自由空间利用声场的波域(柱谐域)[13-14]信息优化次级声源布局，解除了对误差传感器位置的依赖，同时以区域声势能作为控制目标。虽然所选布局在误差点降噪效果不如空间域搜索方法，但在空间声势能降噪量和系统鲁棒性方面表现更优。

本文将文献[12]的工作拓展到三维封闭空间，利用声场的平面波分解构造波域ANC代价函数，进行次级声源布局优化。以刚性壁矩形封闭空间为对象，仿真对比2种传统的空间域方法，并讨论所提方法在实际中的布局优化效果和相关问题。

1 空间域次级声源布局问题

对于封闭空间单频声场的ANC，陈述空间域中的次级声源布局问题，定义评价布局性能的4个指标。

pr=pp+Zq

(1)

式中：pp和pr分别为M×1的初级和残余声压向量；Z是M×L的ATI矩阵；q为L×1的次级声源强度向量。

空间域ANC的代价函数为误差传感器处残余声压平方和,即

(2)

式中：(·)H表示共轭转置；‖·‖2是L2范数。假设(2)式方程组超定(M>L),则最优次级声源强度为q=-(ZHZ)-1ZHpp,由此获得该布局下的降噪量为[2]

(3)

Δ仅说明M个误差传感器位置的降噪量,下面定义另外3个常用的布局性能指标:

1) ATI矩阵的条件数κ(Z)

定义κ(Z)=‖Z‖2‖Z-1‖2,若κ(Z)很大,则ATI矩阵呈病态,ANC系统对外界摄动敏感。

2) 控制功率P

定义P=qHq,是次级声源输出功率的量度。若P过大,会导致控制区域外声级增大,还会引起扬声器的非线性响应。

3) 空间声势能的降噪量ΔE

表示整个封闭空间的降噪量,只与次级声源的布局和强度有关。虽然实际中无法直接测量,但对于简单形状的封闭空间可以利用模态叠加方法进行解析计算[1]。

通过以上叙述可知,在空间域,对于某个次级声源布局,一旦误差传感器布局预先给定,即可估计其降噪性能。将误差传感器处的初级声压pp和相应的所有备选次级声源的ATI矩阵Zc统称为布局优化的“空间域先验信息”。传统的空间域布局优化方法即利用pp和Zc数据,通过具体的优化算法(如SA、GSO等)选择次级声源布局,如图1所示。

图1 次级声源布局优化流程

2 波域次级声源布局优化

利用随机分布的传声器测量声场,经平面波分解获得初级声场和各备选次级声源的波域信息,构造波域代价函数,进行次级声源布局优化。

2.1 基于平面波分解的波域先验信息获取

根据平面波分解,封闭空间声场s(r)可以近似展开为一系列平面波的叠加,这样s(r)可由对应的平面波幅值(plane wave amplitude,PWA)近似表征[15]。这些PWA不包含空间位置信息。实际中,常用随机分布的传声器测量获取声场的PWA。需要说明,ANC关心的局部区域一般远离壁面,因此分解中的倏逝波成分可以忽略[16]。

2.1.1 初级平面波

首先利用Q个传声器采样初级声场,假设平面波基的离散平面波个数为R,由下式计算初级PWA

wp=H†sp

(4)

式中：wp为R×1的初级PWA向量；sp为Q×1的采样声压向量；H是Q×R的平面波分解矩阵,其元素表达式见文献[15]；(·)†表示伪逆。

2.1.2 单位次级平面波

给定L个次级声源,以第l个强度为ql的次级声源单独发声为例,同样用Q个传声器做采样,相应的次级PWA为ws,l=H†ss,l=H†zlql,其中zl是该次级声源到Q个传声器之间的ATI向量。因此L个次级声源产生的次级声场的次级PWA为

ws=H†Zq=Γq

(5)

式中：R×L的矩阵Γ称为单位次级PWA矩阵,其第l列为γl=H†zl,解释为第l个次级声源发声强度为1 m3/s时的次级PWA。(5)式给出了次级PWA和次级声源强度之间的关系。

2.2 波域代价函数

以残余PWA的平方和为代价函数,即

(6)

(6)式只涉及次级声源布局信息,与误差传感器位置无关。由于一般有R>L,因此最优次级声源强度为qWD=-(ΓHΓ)-1ΓHwp,进而可以类似(3)式计算该布局下PWA的衰减量。对比(2)式以最小化误差传感器处残余声压为目标,(6)式利用的残余PWA更能反映控制区域的全空间信息,是面向空间降噪的控制目标。

2.3 次级声源布局优化

2.1小节获得了布局优化的波域先验信息,初级PWA向量wp和单位次级PWA矩阵Γ,均不涉及误差传感器位置信息。之后便可应用具体的布局优化算法选择次级声源布局(见图1),本文采用简单的SA搜索,方法标记为WD-SA。

需要强调,虽然波域方法利用(6)式的代价函数,选出使得残余PWA平方和最小的次级声源布局,但由于实际中采用空间域控制,因此评价所选布局的降噪性能仍需给定误差传感器位置,再计算第1节介绍的4个指标。

3 仿真结果与讨论

仿真采用的模型为刚性壁矩形封闭空间,如图2所示(同文献[2]),尺寸为6 m×2.2 m×2.2 m。以空间几何中心为原点,初级声源位于(-3,0,0.6)。33个备选次级声源和32个误差传感器的位置设置参考文献[2]。

图2 刚性壁矩形封闭空间

3.1 PWA解析值的理论结果

首先考查当获知波域先验信息真实值时,WD-SA的优化结果。在刚性壁矩形封闭空间中,对于单极子产生的声场,容易推导其PWA解析值。

假设单频f下,位于r′处强度为q的单极子发声产生空间声场,由模态理论,任一点r处的声压可近似为[17]

(7)

由于矩形腔中各模态可以看作8个平面波的叠加[16],因此(7)式进一步写为

(8)

式中：(∘)为Hadamard积；kn是第n阶特征波矢[n1π/lx,n2π/ly,n3π/lz]T;uι是如下符号矩阵U的第ι列

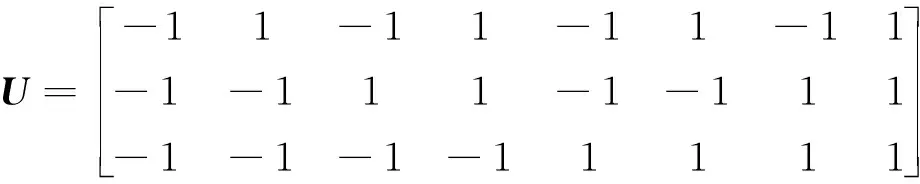
由(8)式可得第n阶声模态对应的8个PWA解析值

(9)

及其传播方向(φ,θ)

(10)

式中：φ为方位角；θ为天顶角。

利用(9)和(10)式,可计算单极子激励下矩形封闭空间声场的PWA解析值及其方向,从而获取波域先验信息wp和Γ,进行次级声源布局优化。本文算例中截取前500阶声模态,得到4 000个平面波。需要强调,各阶声模态对应的平面波的波数不相同,即使传播方向一致,也无法合并。

同文献[2],考查88和176 Hz这两阶桨叶通过频率,比较WD-SA和传统的2种空间域方法,分别标记为SD-SA和SD-GSO。SA算法的参数设置参考文献[2],初始温度为0.9,冷却系数为0.98,搜索重复运行20次取平均结果。GSO算法的具体流程见文献[3]。

图3和图4分别给出了2个频率下3种布局优化方法(SD-SA、SD-GSO、WD-SA)所选布局(针对不同激励次级声源个数L)的性能指标。可见,SD-SA在误差传感器处的降噪量Δ最大,因为其优化目标即使得Δ最大。SD-GSO所选布局的各指标表现较劣。三者的ATI矩阵条件数κ(Z)相差不大。WD-SA虽然Δ不如SD-SA,但能获得明显更好的空间声势能降噪量ΔE,同时所需的控制功率P更小。

图3 88 Hz下3种布局优化方法所选布局的性能指标 图4 176 Hz下3种布局优化方法所选布局的性能指标

3.2 PWA测量估计值的结果

3.1小节探究了波域先验信息解析值下的布局优化效果,但实际中只能通过传声器现场测量来估计wp和Γ(如2.1小节介绍)。本文采用Q=100随机分布的传声器(称为一个传声器组)采样封闭空间声场,并附加信噪比30 dB的零均值高斯噪声作为环境摄动。另外,平面波方向的解析值也难以获知,需通过求解Thomson问题,在球面上均匀选取R个离散传播方向[15],组成平面波基。由于传声器随机布放,不同随机位置可能会产生影响,因此考查50组传声器组。激励次级声源个数L设置为8,SA算法重复运行20次取平均结果。

图5给出了88 Hz下利用PWA测量估计值计算的WD-SA所选布局的降噪量指标,实线表示的相同信噪比下SD-SA的20次搜索平均结果作为参考。可以看到,WD-SA能达到更优的ΔE,但不同随机位置的传声器组的结果相差很大。差异与传声器组对PWA的估计误差有关。离散平面波个数R对结果的影响没有明显规律,可选取较小的R以减少计算量。

图5 88 Hz下利用PWA测量估计值的WD-SA所选布局的降噪量指标(L=8)

由于真实的平面波方向难以获知,因此无法直接计算PWA的估计误差。为此,这里利用PWA进一步做声场重构,计算重构声场的相对平均误差(RME)来间接考查PWA的估计精度,定义如下[18]

(11)

图6给出了初级PWA和单位次级PWA对应的重构RME。同样看到R影响较小。为便于观察,设置图6a)纵轴为对数尺度,发现不同传声器组的初级声场重构RME不同,但大多数在0.1以下,差异不大。对于各备选次级声源的单位次级声场,同一传声器组得到的重构RME差异很大,虽然大多数在0.3以下,但一些组个别次级声源甚至超过0.5。这是因为不同位置备选次级声源产生的单位次级声场不同,同一传声器组在不同待测声场下的重构能力不尽相同。对于不同传声器组,单位次级声场重构RME分布也很不相同。因此,需要针对具体的待测声场,选择较优的传声器组做采样。

图6 88 Hz下100个随机分布传声器重构声场的相对平均误差

联合图5和图6,对比R=100下的第13组和第50组传声器组,前者的降噪效果远优于后者,但观察图6,前者的重构RME劣于后者,其中初级PWA的重构RME分别为0.084和0.057;对于单位次级PWA的重构RME,第13组存在7个在0.21以上,而第50组全部小于0.21。这说明重构RME并不完全对应波域先验信息估计值的布局优化性能。可能的原因是重构RME不能等价于PWA估计误差;或者是不同次级声源的声场贡献作用不同,因而其重构RME对布局优化的影响也不同,对于作用小的次级声源,即使其单位次级PWA的重构RME很大,也不会产生影响;也与波域代价函数的布局优化目标和空间域控制的不匹配有关。

4 结 论

本文利用封闭空间声场的平面波分解构造波域ANC代价函数,优化次级声源布局。主要结论如下:

1) WD-SA利用波域先验信息(初级声场PWA和各备选次级声源的单位次级声场PWA)优化次级声源布局,不涉及具体的误差传感器位置信息。以残余声场PWA平方和作为代价函数,是一种面向全局控制的目标函数,所选布局相比空间域方法能获得更好的空间声势能降噪效果。

2) 实际应用WD-SA需要预先利用传声器采样封闭空间声场,估计其PWA,通过PWA估计值所选的布局可以达到比空间域方法更好的空间声势能降噪量。PWA估计精度影响WD-SA的布局优化效果,其与客观存在的待测声场和传声器位置有关。

3) 下一步研究需关注如何提高PWA估计精度,深入探究PWA估计误差对布局优化结果的影响,并进行实验验证。