基于经度条带划分的星座对地覆盖问题的快速求解算法
宋志明, 刘海栋, 陈晓宇, 王茂才
(1.中国地质大学(武汉) 计算机学院, 湖北 武汉 430074; 2.智能地学信息处理湖北省重点实验室, 湖北 武汉 430078)
随着科学技术的迅速发展,星座应用技术在移动通信、气象预报、遥感探测、军事侦察、资源勘探、灾害监测、导航定位等多个领域发挥越来越重要的作用。在星座应用领域中,对地服务是一个非常重要的组成部分。星座的对地服务,是基于星座中卫星携带的各种样式与功能的星载传感器对地面进行持续或者间断性地服务来实现的。将星座对地服务中涉及到的问题统称为星座对地覆盖问题。目前,已经有很多学者针对星座对地覆盖这一复杂问题进行了相关研究。
网格点法是求解星座对地覆盖问题的一种经典方法。该方法是由Morrison在1973年提出来的[1],而后,有很多学者在此基础上进行了改进[2-4]。网格点法对几乎所有类型覆盖问题都能进行求解,且可以通过增加网格点的数目得到更高精度的结果,但当结果精度要求较高时,算法的效率会大幅度下降。覆盖带法也是卫星技术发展早期常用的一种方法[5-6],而后在很多覆盖问题求解中被广泛应用[7-8]。该方法将卫星在一个时段内扫过的范围近似为一个覆盖带,从而分析星座对地覆盖性能。三角网剖分法是以卫星瞬时位置为节点,将地球表面划分为一组的球面三角形,从而进行性能分析的一种方法[9]。但该方法只能定性判断星座对全球是否能完全覆盖而无法定量计算覆盖率。针对于三角网剖分法的缺点,陈晓宇等[10-12]提出了球面多边形剖分法,可以对结果进行定量计算,可对区域目标进行求解。特征区域分析法是一种基于星座中卫星星下点轨迹,对二维球面进行划分得到一系列区域,进而得到对整个区域的覆盖特性的方法[13-14]。该算法求解速度极快,但只能对Walker星座的连续性覆盖问题进行分析。
有部分专家学者,将覆盖问题等价转换或近似转换为某种数理过程,用数理过程中的相应数理特性来对星座覆盖问题的结果进行间接表征。文献[15-16]通过球面圆的基本几何特性,得到覆盖过程的一些特征点或特征弧段,通过对这些特征几何体的性能来表征对整个区域的覆盖性能。文献[17]将星座对地覆盖问题描述为一个蒙特卡罗过程,通过抽样理论,得到基于蒙特卡罗方法的覆盖率。文献[18-19]使用概率统计模型对其进行分析,得到概率意义下的覆盖特性随时间与空间的变化规律;文献[20-21]将覆盖问题转化为一个卫星和目标位置的函数,通过数值算法求函数零点,从而得到覆盖问题的相关特性;文献[22]将覆盖问题转化为一个微分方程,通过数值积分方法对函数进行求解;文献[23]中,采用数值拟合方法对覆盖特性进行拟合,得到星座对地覆盖问题的拟合函数;文献[24]通过球面几何关系,提出了对全球完全覆盖的判定定理;文献[25]将卫星在一段时间内的覆盖范围看作曲线族,求解曲线族的包络线,并得到包络线与覆盖范围边界之间的关联。文献[26]提出了一种基于变换群的性能分析方法,采用晶体点群理论描述星座。文献[27-28]则采用矩阵对Flower星座对地覆盖问题进行了描述,将星座的空间构型同构为一个二阶或三阶矩阵,从而实现对星座的设计和性能分析。对于这一类求解方法,一般都只对星座对地覆盖问题的某个方面的特征进行建模,因此,一种方法往往也只能得到某个方面的覆盖特性。同时,在数理建模过程中,往往需要进行一些近似处理,因此,得到的结果多是一个近似结果,而且很多时候是定性结果。
本文在本人前期研究的基础上[29],提出一种求解星座对地覆盖问题的高效求解算法—经度条带法。该方法将地面区域划分为若干经度条带,借助于经线的可解析性得到星座对条带的覆盖面积,从而对星座对地覆盖问题进行求解。该方法可对以凸多边形或非凸多边形区域为目标区域的瞬时覆盖问题、连续性覆盖问题与累积覆盖问题进行求解,具有非常广的算法普适性。
本论文的组织结构如下:第一节对经度条带法对地覆盖问题的形式化的符号和基本流程进行描述,并提出覆盖率上下界的基本思想。第二节针对累积覆盖问题和连续性覆盖问题,得到其对应的覆盖率上下界形式。第三节为数值仿真实验,对第一节和第二节中的结果进行仿真验证。第四节为总结。
1 经度条带法对星座对地覆盖问题
1.1 覆盖问题的基本符号表示
对于地面上一点P,其经度与纬度分别记作θP与φP。而对于经度为θ的一条经线记作E(θ)。
将一颗卫星记作S,一个卫星星座记作C,使用符号S∈C表示星座C包含卫星S。将整个地球表面记作G,将地面区域记作R,则R⊂G。地面上的一点P,P∈R表示点P是区域R内的一点。将开始时间为tS结束时间为tE的时间段记作[tS,tE],使用符号t∈[tS,tE]表示t是时间段[tS,tE]内的一个时刻。
本文中,对星座对地覆盖的累积覆盖范围进行分析,并计算对应的空间覆盖率进行分析。
将一颗卫星S在t时刻的瞬时对地覆盖范围记作ΛS(t),星座C在t时刻的瞬时对地覆盖范围记作ΛC(t),则
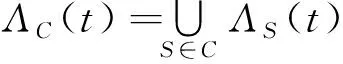
(1)
将一颗卫星S在[tS,tE]时间段的累积覆盖范围记作ΛS([tS,tE]),星座C在[tS,tE]时间段的累积覆盖范围记作ΛC([tS,tE])。
则
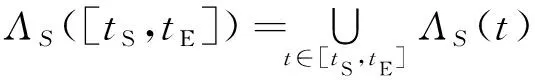
(2)

(3)
而区域目标R的空间覆盖率是指区域目标R中,被星座覆盖的区域面积与区域目标R的面积之比。令m[R]表示对一个区域目标R的面积测度函数,将空间覆盖率记作η,则某时刻t下的瞬时覆盖率为

(4)
时间段[tS,tE]下的累积覆盖率为

(5)
对于公式(4)或公式(5),其计算的难点在于:
1) 星座对地覆盖范围ΛC(t)或ΛC([tS,tE])的表示。
2) 星座对地覆盖范围与任意形状地面区域R相交范围的计算。
3) 任意球面不规则区域的面积度量。
在本文的后续,将提出一种算法,用于解决这3个方面的复杂性。
1.2 经度条带的基本概念
定义1经度条带。1条经度条带是指在地球表面上的2条相邻近的经线之间包围的区域。2条经线之间的经度差叫做经度条带的宽度,2条经线的中间值叫做经度条带的中央经线。中央经度为θ,条带宽度为Δθ的经度条带记作L(θ,Δθ),在不强调条带宽度或者中央经度的时候可以简记为L(θ)。
1条经度条带可以看作经度与中央经线相差小于Δθ/2的点的集合
L(θ,Δθ)={P∈G||θP-θ|<Δθ/2}
(6)
或1组与中央经线的经度差小于Δθ/2的经线的集合
L(θ,Δθ)={E(α)||α-θ|<Δθ/2}
(7)
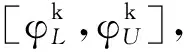
(8)
一个经度条带和一个纬度区间,可以得到一个经度条带的纬度范围。
定义2纬度范围。经度条带上的纬度范围是该经度条带在纬度区间内的区域。经度条带L以Π为纬度区间的纬度范围记作LΠ,在强调经度条带的中央经线与宽度时记作LΠ(θ,Δθ)。则
LΠ={P∈L|φP∈Π}
(9)
则可知,经度条带的纬度范围,是经度条带的一个子集,即
LΠ⊂L
(10)
在有了纬度区间和纬度范围的概念后,给出定义在这两个结构上的度量函数。对于Π,则依据公式(8)与公式(12),在其上定义一个度量‖Π‖

(11)
令m[R]表示对任意一个球面区域R的面积度量。将地球半径归一化为1,则通过球面面积公式可知,纬度范围L[φL,φU](θ,Δθ)的球面面积为
m[L[φL,φU](θ,Δθ)]=Δθ·(sinφU-sinφL)
(12)
则纬度区间度量‖·‖与面积度量m[·]有关系如公式(13)所示
m[LΠ(θ,Δθ)]=Δθ·‖Π‖
(13)
根据经度条带的定义,可将全球划分为若干个等宽度的经度条带的集合,即
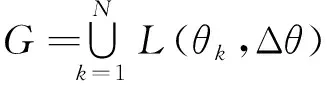
(14)
式中
(15)
则可知,公式(14)得到的经度条带集合{L(θk,Δθ)|k=1,…,N}是对全球的一个划分。
假设R为一个任意形状球面区域,则区域R可以近似划分为若干纬度范围之并。

(16)
式中,Πj为经度条带L(θj)在区域R内的纬度区间。该过程称作对区域的条带划分。
一般而言,1组经度条带并集,与R所对应的区域,并不是严格一致的,因为纬度范围为一个或多个经纬度框区域,而地面区域可以为任意形状。因此,一般而言,会有一部分“误判”区域。将误判区域定义为ε,则
(17)
式中,A/B表示2个集合A与B之间的差集运算。
对于一个特定的区域R和一个经度条带L(θj),其对应的纬度区间Πj(R∩L(θj))可以有多种选择。不同的Πj的选择,将决定对区域的条带划分的不同性质。当然,Πj不能随意选择,而是需要满足一定的合理性条件。一种合理的纬度区间Πj需要满足如下基本条件:
定理1Πj的合理性条件。一种Πj的选择是合理的,当且仅当Δθ→0时,有ε→0。
在本文中,将提供2类不同的Πj的合理选择。
满足Πj合理性条件的球面区域划分策略有多种,如以经度条带L(θj)的中央经线E(θj)与区域R相交的得到的纬度区间作为Πj的选择,即满足Πj的合理性条件。除此之外,还可以有其他多重形式。本文中着重论述2类典型的形式,称作Πj的下界形式与上界形式。
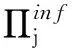
(18)
(19)
则可知
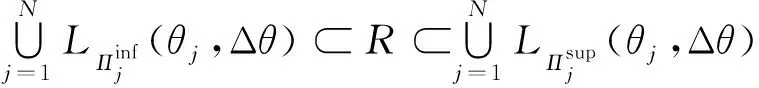
(20)
并且,当Δθ→0,有

(21)
1.3 球面圆盘与经线相交的纬度范围计算
定义4球面圆盘。球面圆盘定义为到球面上某一点P的球面角距离小于等于α的所有球面点的集合。P称作球面圆盘的圆心,α为球面圆盘的半径。球面圆心为P半径为α的球面圆盘,将其记作Θ(P,α),在不强调圆心与半径时可以简写为Θ。
对于一个区域R,其边界记作∂R。则对球面圆盘的边界记为∂Θ,其为一个典型的球面圆。
分析Θ对经线E(θ)的覆盖范围,∂Θ与E(θ),二者可能有0个、1个或者2个交点。
对于经纬度为(θ,φ)的一点,在将地球半径归一化为单位长度的情况下,记该点在直角坐标系下的坐标为(x,y,z),则由直角坐标与球坐标之间的转换公式可知

(22)
假设Θ的中心经纬度为(θ0,φ0),球面圆与经线E(θ)交点纬度为φ,则由公式(22)可知,在交点处满足
cosφcosφ0cos(θ-θ0)+sinφsinφ0=cosα
(23)
则可知,Θ((θ0,φ0),α)与E(θ)相交的必要条件是公式(23)有解,即
cos2φ0cos2(θ-θ0)+sin2φ0≥cos2α
(24)
解得

(25)
则当θ满足(25)式时,Θ((θ0,φ0),α)与E(θ)有交点。而当θ不满足公式(25)时,Θ((θ0,φ0),α)与E(θ)没有交点,此时,Π(Θ∩E(θ))=∅。
考虑二者有交点的情况,假设2个交点分别为M,N,其中M点的纬度大于N点的纬度,则当Θ((θ0,φ0),α)与E(θ)相交时,令

(26)
令

(27)
则

(28)
则球面圆与经线的相交范围为

(29)
1.4 球面圆盘与经度条带相交的纬度范围计算
令Θ为一个中心(θ0,φ0)半径为α的球面圆盘,其与经度条带L(θj,Δθ)相交的纬度范围Π。

分析球面圆盘与经线的相交的性质,根据公式(26)至(29),可以确定球面圆与经线相交的纬度区间的性质。当θ=θ0时,球面圆与经线相交的纬度范围最大,|θ-θ0|越大,球面圆与经线相交的纬度范围越小。则可知,相交区间范围的最小值出现在经度条带的左右两侧经线上。如果θ0∈[θ-Δθ,θ+Δθ],相交区间范围的最大值出现在θ=θ0时,否则,相交区间范围的最大值出现在经度条带的左右两侧构成经线上。
则
Π(Θ∩E(θj-Δθ))∩Π(Θ∩E(θj+Δθ))
(30)

(31)

由此,可以得到球面圆盘与经度条带相交的纬度区间的上下界值。
1.5 任意球面区域与经度条带的相交性计算
假设R为一球面区域,则对任意的球面区域,都可以使用一个球面多边形U对其进行近似表示。一般而言,认为可以使用球面多边形U来完全代替球面区域R。如果希望在论述上更加严谨,可以定义2个球面多边形Uinf与Usup,使得Uinf⊂R⊂Usup。
本文中只考虑球面区域R为多边形区域的情形。
考虑R为一个单连通球面凸多边形。则由简单的球面几何知识可知,区域R可以看作是以R的边界作为边界的一组球面圆盘相交区域。即
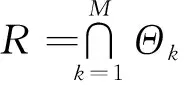
(32)
式中,对任意k,都有∂Θk∩∂R≠∅。
则球面凸多边形与经度条带的相交范围可以表示为
(33)
对于任意球面多边形区域,可以看作是有限球面凸多边形的并交叉补运算,则有
(34)
则根据公式(34),可以得到任意形状球面多边形与经度条带的纬度区间。
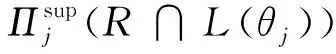
1.6 卫星星座对地覆盖范围
星座C在某个时刻t下对地面的瞬时覆盖范围记作ΛC(t)。在星座对地覆盖问题中,很多情况下,需要的往往不止是某个时刻下的覆盖范围,而是星座在某个时间段下的覆盖的累积效应。
星座在某个时间段下的覆盖累积效应,大致可分为两类不同的需求。在通信、导航等领域,需要满足在特定区域,星座每时每刻都需要满足某种覆盖要求,这种需求称作连续性覆盖需求。而在地面遥感、数据传输等领域,只需要在某个时间段内,存在某个时刻满足某种覆盖要求即可,这种需求称作累积性覆盖需求。
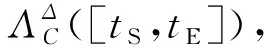

(35)

(36)


(37)


(38)
(39)
1.7 使用经度条带法进行覆盖率计算
则由公式(16)与公式(37),可以得到
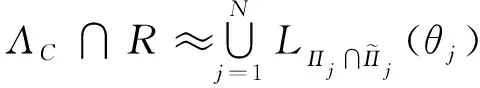
(40)
同样,公式(40)也存在上界形式与下界形式

(41)
将卫星星座C对地面目标R的覆盖率定义为在某个时刻或者某个时段下,星座对地面目标中有覆盖的区域面积与总的区域面积之比。

(42)
则由公式(40)与(42)可知,通过经度条带法,可以将不规则形状的覆盖率计算,转换为区间的计算问题,然后通过简单的区间度量计算,即可得到覆盖率。
则根据公式(20)与(41)可以定义覆盖率的下界ηinf与上界ηsup
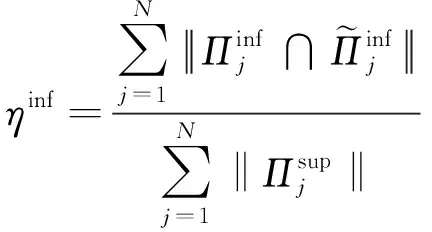
(43)

(44)

由此,可以通过公式(43)与(44)得到覆盖率的上界值与下界值,从而确定当前划分精度下的计算结果真实值所在的范围。
下文将对这两个问题进行论述,从而得到通过经度条带法对任意区域任意形式的覆盖问题的求解算法。
2 星座对地覆盖范围计算

时间离散化的基本方法是,令t0=tS,tN=tE,由此得到时间点的集合T={t0,t1,…,tN},对任意k=0,1,2,…,N,都满足tk=t0+k·Δt,其中,Δt=(tE-tS)/N。使用时间点集合T来代替时间段[tE,tS],来对连续时间段进行求解。


(45)

(46)
通过简单的集合论的结论可知,在任意情况下,都有以下结论

(47)
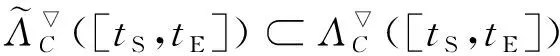
(48)
由此可知,时间离散化策略会使得累积覆盖问题与连续覆盖问题结果带来倾向性的偏差,对连续性覆盖率而言,会使得计算结果比真实值偏大,而对于累积性覆盖率而言,计算结果比真实值偏小。
如果要更为精确地计算连续性覆盖问题与累积性覆盖问题,需要提出其他策略。第一种策略,设计其他求解算法,得到覆盖范围。第二种策略,通过得到覆盖范围的上界和下界来进行计算。
2.1 累积性覆盖问题计算
在进行累积性覆盖问题分析时,由于卫星是周期性的运行的,在进行分析时,需要将时间段进行划分。时间段划分的过程,与时间离散化过程类似。只不过时间段划分的结果并非得到离散的时间点,而是时间段的集合。
T′={[t0,t1],[t1,t2],…,[tN-1,tN]}
(49)
在累积性覆盖问题分析中,每一个时间段的长度可以较长,比如选择0.5个卫星周期。则对于划分的时间段

(50)
则由公式(50),可将星座对一个较长时间段内的累积覆盖问题转换为星座对若干较短时段内的累积覆盖范围的并集。

图1 卫星对经线累积覆盖示意图
如图1所示,AB为经度为θ的经线E(θ),P到Q为卫星星下点轨迹的一段。M和N为同一卫星在2个不同时刻的位置,当卫星星下点在M点时能覆盖该经度条带上最小的纬度点L,当卫星星下点在N点时能覆盖该经度条带上最小的纬度点U。由于卫星的位置是一个随时间连续变化的过程,则在一个时间窗口内卫星对一个经度条带的覆盖纬度区间是一个连续区间。要计算卫星在该时间段内对经线的覆盖纬度区间,只需要该连续区间的边界值即可,即图中所示的U、L点。该经度条带上U、L之间的点是必然可以被覆盖的。
考虑这个时间段内卫星对经线有覆盖的时间区间,记作[tk-1,tk]。则当t∈[tk-1,tk],卫星对经线的覆盖范围下界值与上界值可分别看作是一个以时间t为自变量的函数,分别称为卫星对经线的覆盖下界函数与覆盖上界函数。考虑卫星携带简单圆锥体传感器,也就是说,卫星的对地瞬时覆盖范围为一个球面圆。由文献[25]中的结论,若卫星的星下点轨迹上的每一点的球面曲率半径都大于卫星瞬时覆盖圆的球面半径,卫星对经线的覆盖下界函数与覆盖上界函数均为单峰函数,对于中低轨卫星而言,该结论是一直都成立的。但需要注意的是,如果卫星对地瞬时覆盖范围不是球面圆,而是其他图形,则星座对经线的覆盖下界函数与覆盖上界函数为单峰函数的结论可能不能成立。
而对于单峰函数,经典的最值求解方法三分法可以快速求得函数极值。而对于卫星瞬时覆盖范围不是球面圆的情况,则该方法无效,只能通过时间离散化进行近似求解。
(51)
同时,星座累积覆盖范围与经度条带相交的纬度区间的上下界值可以由(52)~(53)式给出
2.2 连续性覆盖问题计算
则要通过上下界方式来确定连续性覆盖范围,还需要找到连续性覆盖问题的一个下界。
在对连续性覆盖问题进行分析时,同样需要进行时间段划分得到仿真时段集合。

(54)


(55)
而对于星座在时间段[tk-1,tk]内的累积覆盖范围与单颗卫星的覆盖范围之间有如下关系

(56)
并且当Δt→0时有

(57)
由此,得到一个连续性覆盖范围的下界。需要说明的是,累积性覆盖的时间划分可以选择为半个周期,但对连续性覆盖,时间划分的长度为更短的数值,否则可能会导致ΛS(tk-1)∩ΛS(tk)=∅,而令覆盖率的下界值为0,使得结果没有价值。
3 数值实验
通过数值仿真对所提出的经度条带法的性能进行验证,数值仿真时段起始时刻为2020年1月1日00∶00∶00,结束时刻为2020年1月1日01∶00∶00,仿真时长为1 h。考虑一Walker星座,其星座构型为40/4/1,所有卫星都处于高度1 300 km的圆轨道上,轨道倾角为45°。所有卫星除中心引力外,只考虑J2摄动影响。星座中的每颗卫星都携带有相同类型的简单圆锥体传感器,对地面无侧摆。下文中将对累积覆盖问题和连续性覆盖问题进行分析。为了使得结果保持在合适的大小,将为2类覆盖问题,设置不同的传感器参数。
为验证经度条带法在不同类型地面区域的性能,以美国大陆范围为目标。该目标是由3 369个球面点组成的球面不规则凹多边形区域。
在进行数值仿真时,给出“条带精度”的概念:
定义5条带精度。条带精度定义为赤道上1 km的宽度内含有的条带数目。对于L(θ,Δθ),其条带精度κ定义为

(58)
式中,RE为地球半径,单位取km,Δθ为条带宽度,以弧度制表示。
在后续仿真实验中,为了将经度条带法与传统网格点法在计算效率上进行对比,可以在传统网格点法领域,定义和条带精度等价的概念,即1 km2内网格点数目的开平方。从数学角度分析可知,在这种定义下,2种精度可以近似等价,即相同的精度下,2种算法的计算误差相当。
3.1 累积覆盖问题数值仿真
对于累积覆盖问题,考虑传感器半视场角为10°,则在1 h的仿真时间内,星座对目标的累积覆盖率上下界随条带精度变化曲线如图2所示。

图2 星座对目标的覆盖率上下界随条带精度的变化曲线
如图2所示,对于累积覆盖问题,对于不规则形状球面凹多边形目标,经度条带法都可对其进行求解,当条带精度较低时,覆盖率上界与下界结果差别较大,随着条带精度增加,覆盖率的上下界值会收敛为同一个值。

图3 经度条带法与传统网格点法求解累积覆盖问题计算时间随精度变化曲线
当时间间隔为15 s时,经度条带法和传统网格点法在对目标的累积覆盖问题求解时,计算时间随着精度的变化曲线如图3所示。由图3可知,传统网格点法在计算精度增加10倍的情况下,计算时间增加约100倍,而经度条带法在计算精度增加10倍的情况下,计算时间增加约10倍。也就是说,传统网格点法计算时间随计算精度呈平方形式增加,而经度条带法呈近似线性的增加。
3.2 连续覆盖问题数值仿真
对于连续覆盖问题,考虑传感器半视场角为52°,则在1 h的仿真时间内,计算星座对目标的连续性覆盖率上下界结果。
连续性覆盖问题和累积覆盖问题的求解方法有所不同。对于累积覆盖问题,采用单峰函数求极值的方法进行求解,而对于连续性覆盖问题,则依赖于划分的时间间隔的上下界。因此,不同的时间间隔,对于覆盖率上下界值会有较大影响。
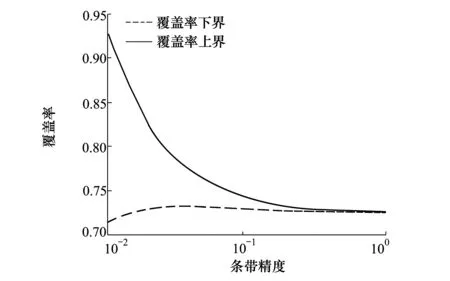
图4 不同时间间隔下星座对目标的连续性覆盖率上下界随条带精度的变化曲线
图4为时间间隔为15 s时,星座对目标的连续性覆盖率随条带精度的变化曲线。对于连续性覆盖问题,对于任意形状球面凹多边形目标,经度条带法都可对其进行求解。对于某个特定的时间间隔下,随着划分精度的提高,覆盖率的上界和下界趋于收敛于同一值。
时间间隔为15 s时,经度条带法和传统网格点法在对目标连续性覆盖计算时间随着精度的变化曲线如图5所示。连续覆盖问题计算时间随计算精度的变化规律,与累积覆盖问题的变化规律相同。

图5 经度条带法与传统网格点法求解连续性覆盖问题计算时间随精度变化曲线
图3及图5仿真实验结果表明,经度条带法在求解累积性覆盖问题和连续性覆盖问题下,都有比传统网格点法更高的计算效率。
4 结 论
本文提出了一种计算星座对地覆盖问题的求解算法—经度条带法,使用形式化的符号对经度条带法的覆盖问题求解过程进行描述,并给出对累积覆盖率和连续性覆盖率的上下界求解算法。仿真实验结果表明,该算法可对连续性覆盖问题和累积覆盖问题进行求解,并且能够对非规则任意形状地面目标进行求解。与传统网格点法相比,该算法具有更高的效率。
与网格点法相比,经度条带法也有一些不足之处,主要体现在,经度条带法只能用于计算以“面积”这个概念为基础的覆盖性能指标,如覆盖率、覆盖面积等。而对于非面积概念的性能指标,如观测仰角计算、区域GDOP计算、区域平均重访时间计算等,该算法目前还无法完成。后续工作,可从对经度条带法的非面积概念性能指标的计算进行开展。

