巧借图像表征,助力学生学习力的提升
郝瑞亚
【摘 要】图像表征能够在数学课堂上化抽象为形象、直观,展现学生的思维过程。教师在教学中,要积极发现学生的图像学习断层,依据学生年龄特点,发展不同画图、识图技能,利用图像表征帮助学生明晰算理,整合知识,拔节思维,最终实现学生学习力的提升。
【关键词】图像表征 学习力 第二学段
图像表征起源于科学研究领域,意指运用简单的图示或图像来表达信息、解决问题,是理解数学的有效渠道。近年来,越来越多的学者意识到图像表征在学生数学学习中的积极意义,并在教学中不断进行尝试。在数学学习中,图像表征能够帮助学生更轻松理解数学概念,明晰算理,尤其在第二学段,解题流程图的引入能够降低学生思维难度,清晰解题流程,在复习阶段利用思维导图能够将零散的知识结构化,强化学生对于知识的理解和掌握。
一、图像表征教学的学段特征
数学新课标将小学阶段分为第一学段(1~3年级)与第二学段(4~6年级),并且对不同学段学生的图像表征能力的要求各不相同,第一学段要求学生“掌握初步的测量、识图和画图的技能”,第二学段要求学生“探索图形的形状、大小和位置关系,掌握测量、识图、画图的基本方法”。这主要与不同学段学生的年龄特点以及认知发展规律有关。第二学段,学生具备了一定的抽象思维能力,教师的教学重点转为引导学生由实物图向条形图、线段图、立体图、解题流程图等过渡,通过图像体现条件、问题以及基本的数量关系,建立一定的解决问题、分析问题的能力。在这一阶段,学生的思维跨度明显增大,图像的优越性也就越发明显,教师一方面要加强线段图、条形图、立体图形的绘制教学;另一方面也要基于图像表征引导学生在题组模块中进行建模,促进学生的深度学习。下面笔者主要以第二学段学生图像表征的教学实践为例进行阐述。
二、善用图像表征提升学生学习力的教学策略
在第二学段的学习中,数学知识的思维性逐渐增强,加之题目的条件增多,思维难度越来越大,尤其在六年级学习立体图形之后,学生的认知要由二维向三维转化,图像表征教学的作用更加明显。以下是笔者在第二学段的教学中所进行的教学实践。
1.聚焦学习需求,填补图像教学空白
1~5年级,学生逐步学习了各种平面图形,如三角形、长方形、正方形、平行四边形、梯形以及圆的特征与画法,在六年级的学习中,学生第一次接触立体图形长方体、正方体以及圆柱与圆锥。一方面,由二维到三维的思维跨度极大,增加了学生理解的难度;另一方面,这部分内容中的习题复杂多变,对学生的抽象思维能力要求较高。借助图形能够化抽象为形象,降低学生的理解难度。但是立体图形的画法在书上并没有专门介绍,因此,教师需要关注到这部分图像教学的空白,及时添加专门的画图训练课,來填补画图断层。
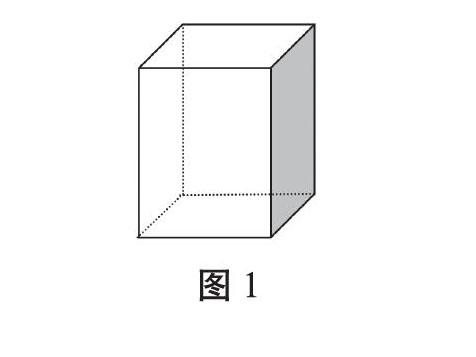
笔者进行了这样的尝试:在六年级上册学习长方体与正方体的特征之后,专门增加了一节画图课,主要教学长方体、正方体的画法,结合习题分析,增加长方体或正方体两两合并之后的图形教学。在教学长方体与正方体的画法时,引导学生遵循“斜二侧画法”,先画正面的长方形,再将上面与右面画成平行四边形,最后利用虚线将看不到的部分补全(见图1)。在学生熟练掌握长方体、正方体的画法后,进一步教学将两个长方体拼在一起的三种不同图形(见图2)。学生画图的过程,同时也是对长方体特征内化巩固的过程,另外两个图形结合在一起,学生能够直观地感受到少了两个重合的面,在做相应题目时思维会更加清晰。
2.图像对比教学,算理越辩越明
图像表征能够清晰地将学生的思路呈现出来,教师能够及时发现学生的思维误区,从而有针对性地进行教学。另外,在计算教学中,适当借助数形结合,可以让算理更加清晰,结果的得出更具说服力。
在苏教版数学六年级上册学习“分数除法”的内容时,有这样一道例题(见图3):
在教学时,学生主要有两种答案:一种是认为只能剪2段,一种认为可以剪6段。教师要求学生将自己的思路画出来之后初见端倪。原来学生的思维误区出现在对“米”的认知不够清楚,一部分学生错误理解为米是总长4米的,导致画图出现错误。明白了学生的错误原因之后,笔者继续“以图辩理”,引导学生讨论发现错误思路中的米比1米还长,最终发现应该先画1米,再找到1米的。通过这样的图形辨析,学生不仅牢牢掌握了分数除法的计算方法,更明晰了与米的区别。
3.巧搭复习框架,提升知识整合
学生对于知识的学习是碎片化且以线性的方式进行的,一单元学习之后,教师需要有意识地引导学生整合所学知识,将点状化的知识连成面、结成网,加深学生对知识的理解,提升融会贯通能力。
复习课中最常见的图像框架莫过于思维导图,学生通过知识导图的建构,将一个单元的知识点连接成知识串,知识之间的联系一目了然。如在五年级下册“因数与倍数”这一单元教学结束后,笔者引导学生回顾本单元的知识,并将之绘制成知识框架图。
除了以上提到的单元知识横向构建外,教师还应该有意识地引导学生对于不同年级的关联内容纵向整理,站在学科的角度来看待在小学阶段学习的某一类知识,从而能够更加系统、全面地理解知识的发展进程。如小学阶段有关分数的知识一共出现在三册教材当中,在三年级上册学生初步认识了分数,是在一个物体中建立“几分之一”的意义,在三年级下册的学习中,分数的意义被拓宽在一个物体、一个计量单位以及多个物体组成的整体中,在五年级下册再次学到分数时给出了单位“1”的定义,概念更具抽象性。除此之外,分数与以前学习的整数的除法关系紧密,被除数相当于分子,除数相当于分母,而在六年级上册学习“比和比例”时,再次将除法算式、分数以及比的概念联系起来。因此,在学习“比”的知识之后,教师可以引导学生对三个概念的发展及联系进行纵向整理,形成知识发展框架图。
4.外显解题流程,见证思维拔节
学生在面对一些难度较高的题目时,常常会觉得无从下手而放弃思考,形成思维惰性,教师可以在平时的教学中有意识地引导学生绘制解题流程图,搭建解题脚手架,化繁为简、层层突破,降低思维难度,缓解学生的畏难情绪。
在六年级下册学习圆柱与圆锥的知识时,学生感觉圆柱与圆锥的体积关系理解起来较为抽象,尤其是碰到变形题时,更加无从下手,且课本上学习的原始体积对比图在变形题中难以起到真正的思维支撑作用。于是笔者带领学生对原始图形进行了一定的改进(见图4)。改进之后,学生能够直观看到在体积相等、底面积相等时高的情况。苏教版数学六年级下册有这样一道题:一个圆锥和一个圆柱底面积相等,体积的比是1∶6,如果圆锥的高是4.2厘米,圆柱的高是多少厘米?学生利用改进之后的图为脚手架,解题思路较为清晰,学生将等底等体积的圆柱一次次叠加之后,可以直观地看出最终圆柱的高是圆锥高的2倍。
图像表征能够将抽象的数学知识更加形象、直观化,教师在教学中要善于发现学生图像学习的断层,积极研发图像绘制课填补空白,引导学生利用图像来表达对条件以及问题的理解,多方位培养学生读图、画图以及利用图像解决问题的能力。通过图像表征在抽象的数学中搭建直观与理解的桥梁,使学生的学习力真正得到了提升。
注:本文为南京市教育科学“十三五”规划课题“图像表征支持儿童数学学习的实践研究”(项目编号:L/2018/246)的研究成果之一。

