雅鲁藏布江桑日—墨脱段岩石圈均衡研究以及虚拟水库诱发地震危险性分析

郭凌冬， 付广裕， 佘雅文,3， 王振宇， 杨君妍

1 中国地震局地震预测研究所(地震预测重点实验室)， 北京 100036 2 中国地质大学(北京)地球物理与信息技术学院， 北京 100083 3 南京大学地球科学与工程学院， 南京 210023 4 中国地震局地球物理研究所， 北京 100081

0 引言

雅鲁藏布大峡谷位于喜马拉雅东构造结，该地水力资源丰沛，米林县至墨脱县之间河谷适宜建设大型梯级水库(赵希涛和魏乐军，2020)，但迄今为止尚未确定建设位置.上述梯级水库一旦建成，总装机容量以及年发电量预计均为世界第二，其巨大的蓄水量在地表形成的载荷势必会对库底及附近区域的岩石圈均衡造成一定影响.该区域构造背景复杂，特别是在1950年和2017年分别发生过察隅8.6级(Ben-Menahem et al., 1974)和米林6.9级(尹凤岭等, 2018)地震(图1)，地震活动背景强烈.因此，研究雅鲁藏布江上大型水库蓄水导致的岩石圈均衡变化及其可能导致的水库诱发地震问题，不仅可以对水库选址提供一定参考，还对我国防震减灾工作具有推动作用.

截至2000年，在全球范围内确定由水库诱发并且具有一定强度的地震超过90个(Gupta, 2002).迄今为止，由水库蓄水诱发的最大地震是1967年印度戈伊纳6.7级地震(Shashidhar et al., 2019; Gupta, 2002)；位于埃及尼罗河流域的阿斯旺水库，在1981年诱发了5.6级地震(Gupta, 2002)；我国的新丰江水库自1962年蓄水后，在水库下游诱发了6.2级的地震，为我国最大的水库诱发地震(丁原章,1989).水库诱发地震的研究大部分是通过库仑应力的变化、孔隙压力的扩散以及断层稳定性的动态变化等进行分析.Talwani等(1984)对断层孔隙压力进行计算，发现水库蓄水导致的断层孔隙压力增加是水库诱发地震的主要原因；Deng等(2010)通过计算水库蓄水引起断层库伦应力的变化，得出紫坪铺水库蓄水诱发汶川地震可能性很低的结论；与之相反，Ge等(2009)认为紫坪铺水库蓄水使汶川地震的发生提前了几十年，然而实际的地壳物性参数、断层几何形态以及震源深度等因素都具有不确定性，因此该文得出的结果尚未被学界普遍接受.与上述研究不同，本研究将从岩石圈均衡状态的角度研究水库建设位置和诱发地震之间的关系.

岩石圈均衡问题，研究人员利用重力/GNSS联测数据得出了一定的研究成果.高尚华等(2016)利用重力/GNSS联合观测数据，提出了计算岩石圈均衡附加力的新方法.需要说明的是，高尚华等(2016)将表征岩石圈均衡状态的物理量命名为“岩石圈垂向构造应力”，但由于该物理量是一个矢量而不是张量，使用“垂向构造应力”表述容易与岩石圈内部的构造应力场相混淆，因此本文将 “垂向构造应力”这一概念修改为“均衡附加力”.佘雅文等(2017)对巴颜喀拉块体东缘的岩石圈均衡分布形态进行分析，发现均衡附加力为正值和负值区域分别容易发生浅源地震和深源地震，表明均衡附加力和地震之间存在着某种对应关系.均衡附加力可以表征岩石圈均衡调整的趋势，大型水库蓄水后在地表形成的巨大载荷必将对岩石圈均衡附加力产生影响，从而影响岩石圈均衡调整的趋势.因此，通过均衡附加力的分布状态寻找适宜于建设大型水库的区域，对减少生命以及财产损失具有显著的应用价值.

本研究通过重力/GNSS观测数据，对雅鲁藏布江林芝段附近的均衡附加力进行计算和分析，从均衡附加力的角度给出适合建设大型水库的位置.首先根据地表重力/GNSS联测数据计算雅鲁藏布江河谷的重力异常场，然后在地壳均一和分层模型下分别计算该河谷的莫霍面深度和均衡面深度，并进一步计算相应模型下均衡附加力的大小和方向.然后对比两套计算结果，探讨均一模型带来的计算误差.最后通过均衡附加力的分布形态圈定适宜建设大型水库的位置，为我国在雅鲁藏布江上水库大坝的选址工作提供参考.

1 雅鲁藏布江河谷的重力/GNSS观测以及数据处理

Fu和She(2017)在雅鲁藏布江大峡谷附近建成了一个由107个测站组成的重力观测网，并进行了一期流动重力观测.在上述观测网的基础上，She和Fu(2020)于2019年进行了扩充观测，形成一个由408个测站组成的观测网(图1b)，为本研究奠定了数据基础.整个观测网中，相邻两个测站之间的平均间距约为5 km，对区域重力异常场有较强的约束作用.本文主要研究雅鲁藏布江桑日—墨脱段的重力异常，所以只采用河谷附近的重力/GNSS观测数据，其分布如图1b中绿色三角形所示.需要特别指出的是，雅鲁藏布大峡谷地势险峻、交通不便，难以进行重力观测，因此大峡谷地区存在数据空白(图1b).图1a中，蓝色五角星表示地壳运动观测网络CMONOC(Crustal Movement Observation Network of China)在喜马拉雅东构造地区的重力观测站(祝意青等, 2012).通过上述四个CMONOC重力观测站，可将喜马拉雅东构造重力观测网连接到拉萨绝对重力观测站，获得绝对重力控制.

重力数据的观测过程遵循Fu和She(2017)的思路，使用两台精度为0.02 mGal的Burris重力仪(B105和B115)进行同步观测.为了减少观测误差，观测方式采取了往返测量，即a→b→c→…→c→b→a.为了保证数据的精度，对交叉点以及测线末端点进行了多次测量.使用LGADJ软件(刘冬至等, 1991)对观测数据进行平差处理，发现重力数据的总体精度为0.02mGal.同时，通过三个Leica GX1230双频GNSS接收器获取重力观测点的高程信息，每个观测点的观测时间为40 min，采样间隔为30 s，垂向观测误差在分米量级以内.

通过如下改正实现雅鲁藏布江河谷布格重力异常的计算：(1)固体潮改正，(2)正常场改正，(3)高度改正，(4)中间层改正，(5)地形改正.其中，中间层改正使用的地壳密度为2.67 g·cm-3.基于ASTER GDEM 2009地形模型(Abrams et al., 2010)，以观测点为中心将区域划分为近场、中场和远场，采用有限元方法对重力数据进行地形改正；并根据Kane(1962)和Nagy(1966)给出的公式，计算观测点周边各个区域地形起伏对该点的影响.对于近场区域(0～2 km)，使用间距为1′×1′的网格地形数据进行改正.类似的，对于中场区域(2～20 km)，使用间距为5′×5′的网格；对于远场区域(20～167 km)，使用间距为10′×10′的网格.雅鲁藏布江大峡谷上游地形起伏较小的区域，地形改正量约为20mGal；雅鲁藏布江大峡谷下游，墨脱段地形起伏较大，地形改正量达到60mGal.同时，使用上述重力改正方法的1至3步，得到雅鲁藏布江河谷的自由空气重力异常.结果显示，布格和自由空气重力异常的均方根误差均为0.2 mGal左右.

2 雅鲁藏布江桑日—墨脱段重力异常剖面

基于图1所示的重力观测结果，通过“陆态网络”的相对重力观测数据以及拉萨观测站的绝对重力观测值，得出雅鲁藏布江桑日—墨脱段河谷的自由空气和布格重力异常场(图2).延续Fu等(2014)和Fu和She(2017)的表达方式，相对可靠的重力异常值在以观测点为中心、10 km为半径所连成的缓冲区内用彩色显示.图2a所示的自由空气重力异常表达的是真实地球相对于参考椭球体的密度变化，与地球表面的地形起伏具有一定相关性.沿着河谷将重力观测站所在位置展开成一条剖面，可清晰地展示自由空气重力异常与地形的相关性.由图2c可以看出，除了米林以西部分地区以外，地形对自由空气重力异常具有较大的影响.与自由空气重力异常相比，布格重力异常消除了地形的影响，反映了地球内部的密度变化.因此，布格重力异常与地表地形的相关性较弱(图2d).图2c和2d中，沿着河谷的观测站存在高程起伏现象，而不是完全遵循沿着河谷前进高程逐步降低的规律.其中林芝以东部分观测站的起伏高达百米量级，该起伏反应了观测站处的地形的变化，也大体反映了观测站与附近雅鲁藏布江河面高程的差异，与分米级以内的观测误差关系极小.

图1 雅鲁藏布江河谷的重力观测以及区域构造简图 (a) 研究区域的地理位置. 蓝色五角星表示陆态网络重力观测站，红框为本研究区域； (b) 研究区域构造简图.绿色三角形表示雅鲁藏布江河谷附近重力观测点,棕色三角形表示非河谷段观测点.红色圆点表示1950年察隅8.6级地震和2017年林芝6.9级地震.蓝色线条表示雅鲁藏布江.红色虚线和深红色的线条分别表示缝合带和断裂带,数据来源于宋键等(2011)、丁林和钟大赉(2013)和Chang等(2015). IYS雅鲁藏布江缝合带; JLF嘉黎断裂带; BNS班公—怒江缝合带; STDS藏南拆离系; V1喜马拉雅块体; V2-1 拉萨块体; V2-2那曲块体; V2-3墨脱察隅块体; V3羌塘块体.Fig.1 The gravity network along the Yarlung Zangbo River and the local tectonic structures (a) Location of the study area. The five-pointed stars denote the CMONOC stations. Red box denotes the study area； (b) Tectonic sketch of the study area. The green and brown triangles denote the gravity stations. The red dots denote the 1950 M8.6 Zayu earthquake and 2017 M6.9 Nyingchi earthquake, respectively. The blue line denotes the Yarlung Zangbo River. The red and crimson lines denote suture zone and fault zone, respectively(after Song et al., 2011; Ding and Zhong, 2013; Chang et al., 2015). IYS denotes the Yarlung Zangbo suture zone; JLF denotes the Jiali Fault; BNS denotes the Bangong-Nujiang suture; STDS denotes the Southern Tibet detachment system; V1 denotes the Himalayan block; V2-1 denotes the Lhasa block; V2-2 denotes the Nagqu block; V2-3 denotes the Mêdog-Zayu block; V3 denotes the Qiangtang block.

据图2b可知，雅鲁藏布江河谷桑日至墨脱段的

图2 雅鲁藏布江桑日—墨脱段的重力异常 (a) 自由空气重力异常； (b) 布格重力异常； (c) 自由空气重力异常剖面； (d) 布格重力异常剖面.Fig.2 Gravity anomaly of the Yarlung Zangbo Valley from Sangri to Mêdog (a) The free-air gravity anomaly; (b) The Bouguer gravity anomaly; (c) The profile of free-air gravity anomaly; (d) The profile of Bouguer gravity anomaly.

布格重力异常均为负值，在雅鲁藏布大峡谷上游从西到东表现为由小到大再到小的变化趋势，大峡谷下游墨脱段从东北到西南表现为增大趋势.上游的布格重力异常在西端最小达到-500 mGal，在米林西侧的高值区达到-330 mGal；下游墨脱段最大布格重力异常值达到-350 mGal.雅鲁藏布大峡谷上游河谷海拔变化基本平稳(图2d)，因此米林西侧的布格重力异常高值不是由均衡补偿引起的.前人研究表明，米林西侧既无高密度矿藏(Hu and Yao, 2018)，也无地壳流(Zhao et al., 2013).因此，该地的布格重力异常高值主要反映了莫霍面的相对隆升.

滕吉文等(2006)通过重力异常场对喜马拉雅东构造结的地壳结构进行研究，发现在亚欧板块与印度板块的挤压碰撞下，东构造结的高密度物质向北移动.Jiménez-Munt等(2008)依据重力异常等数据，计算了西藏地区的岩石圈厚度.Bai等(2013)和Jin等(1996)基于西藏地区重力异常数据，发现印度板块俯冲到了欧亚板块下方.Jordan和Watts(2005)通过重力异常等数据确定了印度板块与欧亚板块碰撞区岩石圈的有效弹性层厚度.He等(2014)利用布格重力异常资料对藏北的均衡异常进行了研究，约束了藏北历史演化的地球动力学模型.上述研究均覆盖了此次的研究区域，但本研究依据密集的高精度地表观测数据展开，因此具备更高的可信度.

3 雅鲁藏布江桑日—墨脱段岩石圈密度结构

依据图2所示的布格重力异常数据和高程数据，可进一步反演区域地壳厚度分布和上地幔总体结构等深部信息.考虑到重力反演的多解性，利用布格重力异常数据反演岩石圈的密度构造时，需要建立相对可靠的岩石圈密度初始模型.本文以Hu等(2018)基于瑞利波相速度得到的喜马拉雅东构造结地壳速度结构为基础，使用速度和密度之间关系的经验公式(Wang et al., 2018)：

(1)

本文以图1所示的重力测线西端点为起点，对雅鲁藏布江河谷展开成的剖面进行密度结构反演.采用NGA(Northwest Geophysical Associates)开发的GMSYS(Gravity/Magnetic Modeling Software)软件反演二维地壳密度结构，具体步骤如下：(1)基于地表观测获得河谷布格重力异常数据(图3a)；(2)根据地壳速度结构(Hu et al., 2018)、莫霍面深度(Xu et al., 2013)和沉积层数据(Wang et al., 2014)建立初始地壳密度模型；(3)使用GMSYS正演初始密度模型对应的布格重力异常场；(4)利用非线性参数的最小二乘估计算法(Marquardt, 1963)反演地壳密度结构.经过反复拟合，得到最优的地壳密度结构(图3b).反演结果表明，雅鲁藏布江桑日—墨脱段河谷下部的地壳结构有明显的分层特征，上地壳密度的变化范围是2.6 g·cm-3至2.8 g·cm-3，下地壳密度为2.85 g·cm-3，地幔密度为3.2 g·cm-3.上述密度结构均是通过Hu和Yao(2018)给出的区域地壳速度结构推算得来，界面的差异主要是通过重力数据反演得到.

图3 雅鲁藏布江桑日—墨脱段分层地壳模型 (a) 观测与模拟布格重力异常; (b) 地壳密度结构,红色三角形为各个城市在测线上的投影位置.Fig.3 Layered density model along the Yarlung Zangbo River from Sangri to Mêdog (a) The observed and simulated Bouguer gravity anomalies; (b) The inversed crustal density structure. Red triangles denote the location of cities.

正演的布格重力异常结果与观测结果之间拟合程度反映了地壳结构的可靠性(Deng et al., 2014; Zhang et al., 2017).本文正演值与观测值之间的拟合结果如图3a所示，雅鲁藏布大峡谷上游正演值与观测值的均方根误差为1.33 mGal，下游的均方根误差为3.98 mGal，整条河谷的均方根误差为1.79 mGal.反演得到的莫霍面深度与前人的研究结果基本一致(Wang et al., 2019; Xu et al., 2013; Peng et al., 2016; She and Fu, 2020)，与Wang等(2019)反演的地壳密度结构也具有很好的一致性.

图3b显示，雅鲁藏布大峡谷上游的上地壳与下地壳密度偏大，中间地壳的密度偏小，下游墨脱段的地壳密度由上到下呈现增加的趋势.雅鲁藏布大峡谷上游莫霍面从西到东的变化趋势为“深-浅-深”，在米林西侧莫霍面深度达到最小值，下游的莫霍面从东北至西南逐渐升高.雅鲁藏布大峡谷上游的地壳在20～40 km深处存在一个较大的低密度层(图3b)，该低密度层的空间分布与地震波层析成像的低速层以及大地电磁反演的低电阻率带相一致(Hu and Yao, 2018; Lin et al., 2017; Peng et al., 2016).在含水量、高温和化学成分的综合作用下，该地区的中地壳地震波速和电阻率出现异常(Hu and Yao, 2018)，同时也出现地壳低密度异常的现象.

上述地壳结构表明，莫霍面在米林西侧存在明显的上凸.该地区位于构造单元交界处，米林西侧的雅鲁藏布江缝合带(IYS)基本呈东西走向，米林东侧急转至东北西南走向，藏南拆离系(STDS)与雅鲁藏布江缝合带(IYS)在米林处交会(图1).沿着雅鲁藏布大峡谷上游的重力测线在米林处与雅鲁藏布江缝合带(IYS)交会，从拉萨块体穿过缝合带到达喜马拉雅块体.布格重力异常在米林附近呈现高值，因此反演得到的莫霍面呈现出隆起的趋势.米林西侧的雅鲁藏布江断裂是右旋走滑断裂(宋键等，2011)，米林东侧的东久—米林断裂为左旋走滑断裂(Zhang et al., 2004)，藏南拆离系(STDS)为一系列的低角度正断层(Burchfiel et al., 1992).Chang等(2015)发现喜马拉雅东构造结的岩石圈形变具有垂直连贯性，地下块体的运动与地表运动具有相同的趋势.通过米林附近断裂带性质可以推断地下块体的运动趋势，认为米林南部地体分别向东西移动，使得地壳破裂变得易碎并形成了地幔上涌通道，导致此处莫霍面抬升.该解释也得到了前人研究的证实，Peng等(2016)对喜马拉雅东构造结的地震P波速度异常进行研究，发现米林附近的地幔物质存在上涌特征.Dong等(2016)对该区域的大地电磁进行了研究，该研究认为在印度板块的俯冲作用下深部热地幔物质通过薄弱区域上涌，流体状物质的上涌和横向扩散降低了局部黏度，逐渐将地壳从薄弱区域推离，于是地壳呈现出“东-西”伸展的趋势，该过程类似于洋中脊的扩张.综上所述，米林西侧莫霍面的上凸可归因于地幔物质侵入缝合带.

4 雅鲁藏布江桑日—墨脱段均衡附加力分析

在地质构造时间尺度下，密度较小但相对坚固的地壳漂浮在密度较大但相对柔软的地幔之上.当地壳无外力作用而处于均衡状态时，均衡面和莫霍面处于同一位置(Fu et al., 2014).反之，当地壳受到垂向外力作用时，莫霍面与均衡面发生分离，地壳处于非均衡状态.此时莫霍面和均衡面之间的剩余物质因壳幔之间的密度差而产生附加浮力，需要岩石圈挠曲变形产生的弹性力来维持平衡.该弹性力即为均衡附加力，原则上与附加浮力大小相等且方向相反，因此可以通过附加浮力来计算岩石圈承载的均衡附加力.均衡附加力可以定量地表征岩石圈均衡状态，从而有助于确定适合建设水电站的位置.

4.1 均一地壳模型

莫霍面是近地表最大的一个密度不连续面，是介于地壳和地幔之间的一个化学界面，也是地震波速产生显著跳跃的界面(Fu et al., 2014).莫霍面深度的起伏变化可以通过重力数据反演得到(王谦身等, 2009).为了简化计算，布格重力异常可以简化为由布格板(密度层)厚度变化引起的(Bagherbandi, 2012)，而地壳与地幔之间的密度差异为密度层的密度.因此，可以用密度层的变化近似表示莫霍面的变化.假设雅鲁藏布江河谷下方的地壳均一且密度为2.67 g·cm-3，该密度相当于大地水准面以上物质的平均密度，则莫霍面深度附近密度层的变化可以通过布格重力异常转化得到.如果有一个范围比较大且厚度为h的密度层出现在地表以下深度为H的地方，以Δρ表示此密度层的密度，则该密度层在地表所引起的重力变化可以由如下公式表示(郭俊义, 2001)：

(2)

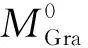
(3)

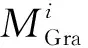
同样，将重力观测站所在位置展开成一条剖面(图4)，大峡谷上游从桑日西端至林芝东端，下游从墨脱东北至墨脱西南.图4b中蓝色曲线表示均一模型下的莫霍面深度，大峡谷上游地壳厚度(莫霍面深度)从西到东展现出由厚到薄再到厚的整体分布态势，下游从东北到西南表现为由厚到薄的分布态势.在整条测线上，桑日东侧莫霍面深度达到最深为68 km，最浅处在米林西侧为62 km.

目前存在多种维持岩石圈均衡状态的密度补偿模型，其中最著名的是Airy均衡模型.该模型假设地壳和地幔的密度均为常数，莫霍面的深度与地表载荷成正比(Zhang et al., 2014).基于Airy均衡模型，当岩石圈处于均衡状态时，莫霍面深度和地表高程之间存在如下关系(郭俊义, 2001)：

(4)

其中，r是山根的厚度，H0是大地水准面以下地壳的平均厚度，ρt是大地水准面以上物质的平均密度(2.67 g·cm-3)，Δρ是壳幔密度差异(0.63 g·cm-3).基于Xu等(2013)的接收函数研究结果，喜马拉雅东构造结平均地壳厚度H0约为67 km.图4b中，红色曲线表示均衡面(均衡条件下的莫霍面)深度，可以看出均衡面深度受地形影响很大；其中大峡谷上游的均衡面深度基本在62～68 km之间变化，下游的均衡面基本在52～57 km之间变化.由于观测站的高程有变化，导致大峡谷上游最东端均衡面有小范围变深的异常.重力观测站总体上沿着河谷布设，但河谷与旁边道路的高差较大，导致图2c所示的地形起伏变化.图2c表示的是重力观测站的高程而不是河面的高程，因此出现图2c中下游高程比上游高程高的情况.在Airy均衡模型下地形与均衡面具有很大相关性(郭俊义, 2001)，因此林芝以东均衡面出现了异常变化.

图4 雅鲁藏布江桑日—墨脱段的布格重力异常、均衡面以及莫霍面深度 (a) 实测布格重力异常,红色三角形表示各个城市在测线上投影的位置； (b) 均一地壳模型下莫霍面和均衡面深度, 蓝色线条表示莫霍面深度,红色线条表示均衡面深度； (c) 分层地壳模型下莫霍面和均衡面深度,图例同(b).Fig.4 The BGAs, isostatic surface and Moho depths along the Yarlung Zangbo River between Sangri and Mêdog (a) The observed Bouguer gravity anomalies. Red triangles denote the locations of the cities; (b) The depths of the Moho and the isostatic surface under the homogeneous crust model. Blue and red lines denote the Moho and the isostatic surface depth, respectively; (c) The depths of the Moho and the isostatic surface under the layered crust model. Legends are the same as (b).

据图4b可知，通过布格重力异常计算得到的莫霍面深度和基于Airy模型计算得到的均衡面深度之间存在差异.如果莫霍面和均衡面的深度十分接近或者相等，则该地处于均衡状态，即地壳的自重等于其所受浮力(Forsyth, 1985).但是，若两者的深度差异较大，则该地区处于不均衡状态.二者差异越大岩石圈越不均衡.根据前人的研究(Fu and She, 2017; 佘雅文等, 2017; 高尚华等, 2016)，均衡问题可以转化为密度界面扰动补偿的加载问题.当均衡面和莫霍面深度存在差异时，两者之间的剩余物质就会产生附加浮力，附加浮力需要岩石圈承载的弹性力去平衡，该弹性力即为均衡附加力.该附加浮力与岩石圈受到的均衡附加力大小相等、方向相反.考虑均衡面和莫霍面深度的不同、壳幔密度的差异，基于均一地壳模型的均衡附加力可表示为(高尚华等, 2016)：

Pvertical=(MGra-MTopo)(ρM-ρC)g

=(MGra-MTopo)Δρg,

(5)

其中，g为重力加速度，ρM为地幔密度，ρC为地壳密度，Δρ为剩余密度(0.63 g·cm-3).通过公式(5)可求出雅鲁藏布江河谷桑日—墨脱段的岩石圈均衡附加力,其中正值表示该处受到的均衡附加力向上，负值表示均衡附加力向下.

通过图5中红色曲线可知，雅鲁藏布大峡谷上游的均衡附加力在-20～20 MPa之间变化.从最西端至测线220 km的位置，均衡附加力基本为正值，220 km以东基本为负值.大峡谷下游的均衡附加力在50～70 MPa之间变化，远大于上游的均衡附加力.测线180～220 km之间河谷的均衡附加力向上且数值较小，甚至出现了0 MPa的测点，在地壳均一模型下这段河谷相比较于其他河谷更接近均衡状态.本研究与Fu和She(2017)的计算结果基本一致.大峡谷上游东侧均衡附加力计算结果出现急剧减小的异常点，亦为观测点与河平面海拔出现显著差异所致.Airy均衡模型下均衡面的深度与地形高度相关(郭俊义, 2001)，在求解均衡附加力时将这一信息带入了最终结果.

图5 雅鲁藏布江桑日—墨脱段河谷的岩石圈均衡附加力 红色线条表示基于均一地壳模型的岩石圈均衡附加力,蓝色线条表示基于分层地壳模型的均衡附加力, 红色三角形表示各个城市在剖面上的投影位置.Fig.5 The isostatic additional force of lithosphere along the Yarlung Zangbo River between Sangri and Mêdog The red line represents theisostatic additional force under the homogeneous crustal model, the blue line represents the one under the layered crustal model. Red triangles denote the locations of the cities.

4.2 分层地壳模型

基于均一地壳模型的均衡附加力计算相对简单，但是分层地壳模型更符合实际，因此本文基于分层地壳模型计算了均衡附加力.与均一地壳模型类似，当某处的均衡面与莫霍面深度相同，则该处岩石圈处于均衡状态.当莫霍面与均衡面的深度之间存在偏差时，两者之间的剩余物质就会产生附加浮力，需要岩石圈承载的弹性力去平衡.某处莫霍面与均衡面的偏差越大，岩石圈就越不均衡.基于Airy均衡模型理论，根据地壳分层的密度结构，可以得到在地壳分层情况下的均衡面深度(王振宇等, 2018)：

+Hn-1ρn-HρM]/(ρn-ρM),

(6)

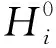
分层地壳模型下，雅鲁藏布江河谷的岩石圈均衡附加力剖面如图5中蓝线所示，正值表示均衡附加力向上，负值表示均衡附加力向下.通过对比均一模型与分层模型下求得的均衡附加力，可以发现两者的变化趋势基本一致.从测线最西端至测线230 km处的均衡附加力的方向向上，米林段的均衡附加力向下，下游墨脱段的计算结果为正值；从林芝到大峡谷之间，均衡附加力在两种模型下的计算结果在方向上不一致，但总体变化趋势基本相同.上述结果与He等(2017)对西藏地区岩石圈均衡状态的研究结果具有一致性，即朗县以东附近的岩石圈基本处于均衡状态，其他地区为非均衡状态(图5).

相对于均一地壳模型下的计算结果(图4b)，分层模型下莫霍面和均衡面深度之间的差异更大(图4c)，该差异与地壳分层结构相关.两种模型下均衡附加力的计算结果差异较大，最大差异达到20 MPa.总体来说，基于分层模型的计算结果与前人结论更加接近(Peng et al., 2016; Wang et al., 2019).因此，若希望得到精度较高的岩石圈均衡结果，应使用分层地壳模型.

4.3 雅鲁藏布江水库诱发地震风险分析

水库诱发地震与大型水库的蓄排水有关，是一种发生在库区及其附近的特殊地震活动(周斌等，2010).水库蓄水会在地表形成载荷，影响周围岩石圈均衡，因此可能诱发地震.

水库蓄水在地表形成的载荷对地壳具有向下的加载作用，通过对岩石圈均衡附加力的方向与水库加载的方向进行比较，可以确定河谷的哪些地方适合建设大型水库.如图6a，若水库建设在岩石圈均衡附加力向上的区域，大量水体的自重会与部分均衡附加力相互抵消，使区域岩石圈更加均衡，从而不容易诱发地震；相反，如果在均衡附加力向下的区域建设水库(图6b)，大量水体的自重会使岩石圈变得更加不均衡，从而容易诱发地震.因此，岩石圈均衡附加力向上的区域适宜建设大型水库.

图6 水库蓄水前后岩石圈均衡附加力变化示意图 (a) 均衡附加力向上时水库蓄水后均衡附加力的变化； (b) 均衡附加力向下时水库蓄水后均衡附加力的变化.Fig.6 The variation of the isostatic additional force before and after impoundment (a) The variation of the isostatic additional force after impoundment when the isostatic additional force is upward. (b) The variation of the isostatic additional force after impoundment when the isostatic additional force is downward.

图5表示岩石圈均衡附加力的大小与方向，在雅鲁藏布江米林段的均衡附加力为负值.假如在米林附近建设大型水库，水库蓄水在地表形成的载荷会使岩石圈更加不均衡，容易诱发触发地震.因此，从岩石圈均衡的角度来讲，米林附近不适合建设大型水库.相反，在米林上游约100 km的朗县附近，岩石圈均衡附加力为正值(图5)，适宜建设大型水库，该处水库蓄水会使岩石圈更趋于均衡，不易触发地震.因此，若在雅鲁藏布江上建设大型水库，建议建在朗县附近，以减轻水库诱发地震的风险.

5 结论

本文首先基于雅鲁藏布江河谷的高密度地表重力观测数据，经过一系列改正，得到桑日至墨脱段的重力异常场.然后分别基于均一和分层地壳模型，通过布格重力异常数据反演河谷底部的莫霍面深度，根据Airy均衡模型计算出河谷区域的均衡面深度.随后依据莫霍面与均衡面之间的差异计算岩石圈所承载的均衡附加力，并据此对雅鲁藏布江未来大型水库建设伴随的诱发地震风险进行了讨论.得到如下主要结论：

(1)桑日至墨脱之间河谷的布格重力异常在-500 mGal与-330 mGal之间变化.沿着河流的方向，大峡谷上游的布格重力异常呈现出由小到大再到小的变化趋势，下游则表现出逐渐增大的趋势.

(2)大峡谷上游中地壳存在低密度层，河谷下游的地壳密度从浅到深逐渐增大.大峡谷上游的莫霍面深度自西向东呈现“深-浅-深”的变化趋势，最浅处位于米林西侧，深度约为52 km.大峡谷下游莫霍面深度自东北至西南逐渐变浅.

(3)基于分层地壳模型的岩石圈均衡附加力计算结果表明，米林附近的均衡附加力为负值，其他地区均为正值.下游均衡附加力自东北至西南呈现出逐渐变小的趋势，最小值为39 MPa.

(4)米林附近的岩石圈均衡附加力为负值，不适宜建设大型水库.从岩石圈均衡的角度来看，若将大型水库建设在朗县附近，将显著降低诱发地震风险.