基于卫星观测的上游等离子体β与磁层顶厚度、速度等特征参数关系的统计研究

李宏硕， 吕建永， 王明， 袁换只， 周悦

南京信息工程大学数学与统计学院空间天气研究所， 南京 210044

0 引言

磁层顶是太阳风等离子体与磁层等离子体之间的边界层，也是将磁层内部磁场和太阳风冻结磁场分开的电流片.在这里，两区域相互作用，有诸如磁场重联(如：Paschmann et al.，1979；Sonnerup et al.，1981；Shi et al.，2005)、扩散(如：Treumann and Sckopke，1999)、脉冲穿刺(如：Lundin et al.，2003)、非线性开尔文-亥姆霍兹波(如：Hasegawa et al.，2004)等物理过程，这些过程可以将太阳风中粒子的质量、动量和能量转移到磁层区域，进而直接或间接地影响磁层结构以及其中各种物理过程的发生，对空间环境安全产生巨大影响.磁层顶区域也是研究磁场重联这一重要物理过程的天然实验室，关于在该区域发生的磁重联研究也日益受到人们的关注并取得了许多重要的成果(如：Fu et al.，2019a，2019b；Peng et al.，2017).有鉴于该区域的重要性，自Chapman和Ferraro于1931年第一次提出磁层顶的概念(Chapman and Ferraro，1931)，以及Cahill和Amazeen于1963年，第一次从“探索者12号”宇宙飞船的数据中实际观测到明确的磁层顶结构以来(Cahill and Amazeen，1963)，人类便从未停止对磁层顶的观测与研究(如：Berchem and Russell，1982；Le and Russell，1994；Phan and Paschmann，1996；Hasegawa，2012；Xiao et al.，2020).

磁层顶的厚度、速度、电流密度作为其重要的特征参数，受到人们的广泛关注.然而之前的研究多集中于磁层顶日侧(如：Berchem and Russell，1982；Le and Russell，1994；Phan and Paschmann，1996；Paschmann et al.，2018).因为普遍认为在该区域，磁层磁场和太阳风冻结磁场的对抗最强，进而产生的诸如磁场重联等的物理过程也就最强，对磁层的影响也最大.而由于磁层顶侧翼处发生的相互作用强度相对不高，对地球影响相对较小，早期又受限于技术原因，获取侧翼数据较为困难，因而对该区域的研究相对较少.随着科技进步，更多更先进的卫星穿越磁层顶探测到的磁场、粒子数据为我们提供了研究更多、更大范围磁层顶内部结构的机会.

Paschmann等(2005)借助ISEE和AMPTE的数据研究了晨侧近尾磁层顶的物理特性，给出了该区域的宏观特征参数，并根据瓦伦关系(磁层顶的上下游之间，等离子体速度变化和局地阿尔芬速度变化之间的比例关系)，划分了旋转不连续(RD)和切向不连续(TD).Haaland等先后利用Cluster、THEMIS、MMS任务卫星穿越磁层顶的数据，计算并给出了晨昏两侧磁层顶的一系列宏观参数，这些研究都表明，磁层顶诸如电流片的运动速度、厚度、电流密度等宏观参数上，存在持续的晨昏不对称性(Haaland et al.，2014，2019，2020).对于这种现象，目前可能的几种解释是：(1)近晨昏两侧磁层顶磁鞘区域内的动压和磁场场强存在差异；(2)晨昏两侧磁层顶受磁层内部物理过程影响；(3)晨昏两侧磁层顶附近的等离子体相对磁场速度不同(宋小健，2019).但其真实原因尚无定论，有待进一步研究.

临近磁层顶的磁鞘参数——诸如离子密度、离子温度、磁场强度等等，存在一定的晨昏不对称(Walsh et al.，2014).磁层顶特征参数的晨昏不对称性，是否是由上游相关参数的不对称造成的，值得研究和讨论.β是等离子体热压和磁压之比，作为重要物理参数对磁层顶的各个参数及物理过程有重要影响，这在日侧已经被多次证实(如：Zhang et al.，2019).Le和Russell(1994)通过对ISEE数据的分析和研究发现，当上游β更大时，磁层顶厚度往往更薄;Phan等(1996)通过对AMPTE数据的分析证实了磁层顶厚度与上游β值之间存在和之前研究相似的相关性，而且他们发现磁层顶的法向运动速度与上游β值也存在相关性，即更高的β值对应更快的磁层顶运动速度.与此同时，β值与磁场重联之间的相关性也被多次讨论.Sonnerup(1974)指出，上游等离子体β越小，磁层顶区域发生的磁重联率更高，当β值足够大时重联就会停止.Phan等(2010)利用WIND卫星数据研究发现，磁层顶两侧区域β值差别较大时，只有磁场剪切角较大的情况下才有重联现象发生，而两侧β值差别较小时，剪切角无论大小都有重联现象发生.随后，Phan等(2013)利用THEMIS卫星数据进行研究，也得到了类似的结果.然而，这些结果主要集中关注了日侧区域的磁层顶，而对侧翼磁层顶相关参数及物理过程与β的相关性，以及侧翼磁层顶附近β情况的研究尚不多见.

本文依据Cluster(C3)卫星的观测数据，通过搜集筛选磁层顶穿越事件，确定磁层顶位置，计算了低纬侧翼磁层顶包括运动速度、厚度、电流密度在内的大尺度参数，并对近磁层顶磁鞘侧离子的β值进行统计，分析研究了低纬侧翼磁层顶的参数及物理过程与上述β值的相关性.本文第一章介绍了数据来源以及磁层顶穿越事件的确定方法.同时说明了本研究所用的，包括坐标系转换、穿越时刻和磁层顶区域定位、磁层顶大尺度参数计算、TD和RD划分等在内的一系列方法.在第1节，本文给出了相关的统计结果.第2节，对结果进行总结.

1 数据和方法

1.1 Cluster卫星数据

Cluster由四颗卫星(C1，C2，C3，C4)组成，于2001年2月起正式工作直至今日.其主要目标是研究包括磁层顶在内的关键区域的小尺度等离子体结构，并据此搭载了相应的仪器.卫星的轨道平面相对于惯性空间是固定的，因而每年可对磁层进行360°的完整扫描(Escoubet et al.，2001).四颗卫星组成四面体结构编队飞行，大约于5月中旬到7月中旬期间穿过晨侧磁层顶，于10月到12月初期间穿过昏侧磁层顶(Haaland et al.，2014).

本文重点对C3卫星，2001年12月至2009年11月的数据进行分析.应用了C3上搭载的磁通门磁强计(FGM)测得的磁场数据，以及离子光谱仪(CIS)中的热离子分析仪(HIA)测得的相关离子数据进行统计计算.本研究中，应用两种磁场数据，分别为高分辨率数据(1 s 5个数据)和低分辨率数据(4 s一个，对应仪器中的旋转分辨率)，应用的离子数据分辨率为4 s一个，相关数据可在https:∥csa.esac.esa.int/csa-web/#search网站中获取.

1.2 穿越事件的确定

本文主要以Karlheinz Trattner, Steven Petrinec和Stephen Fuselier提供的磁层顶穿越列表为基础确定磁层顶穿越事件，具体列表可由https:∥www.cosmos.esa.int/web/csa/bow-shock-magnetopause-crossings-2001—2013网站获得.该列表提供了C3卫星在2001年12月至2009年11月期间发生的6845次磁层顶穿越事件的时间.本文将粒子密度、磁场、温度、粒子能量通量等参数的突变作为评判依据，并辅以当时的卫星位置对这六千多个穿越事件进行了再分析和再筛选，使得所确定的磁层顶穿越时刻更加准确.具体方法如下：

首先，读取穿越列表给出的每个穿越事件的穿越时刻toc，将toc之前2.5 min和之后2.5 min之间，共5 min的时段作为研究时段.读取研究时段内GSE坐标系下的低分辨率磁场数据、卫星位置数据、离子速度数据、离子密度数据以及离子能量通量数据.通过磁场、离子密度、离子速度的突变，并结合卫星所在位置，确定磁层顶穿越事件，同时去除作为判据的参量在研究时段内数据严重缺失的事件.例如，原穿越列表给出，C3卫星于2002年1月13日14∶54穿过磁层顶.以此给定的穿越时刻为基础，如图1，画出了该穿越时刻前后共5 min的磁场和离子参数图.由图1a、1b、1e可以看出，在14∶53∶45左右，各能级的离子通量发生明显变化，同时伴有离子数密度和离子温度的突变.由图1c和图1d可以看到磁场以及离子速度的方向和大小在14∶53∶45左右同时出现较大变化.结合横坐标所示卫星所处的位置，确定该事件为磁层顶穿越事件.

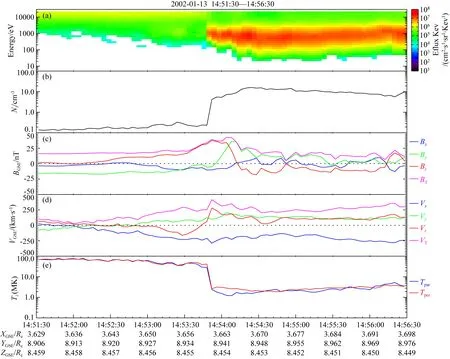
图1 按穿越列表画图辨别磁层顶穿越事件 (a) 离子能量通量; (b) 离子数密度; (c) GSE坐标下的磁场三分量(磁场x方向上的分量由蓝色曲线表示，y方向上的分量由绿色曲线表示，z方向上的分量由红色曲线表示，总磁场由粉色曲线表示); (d) GSE坐标下的离子速度三分量 (速度x，y，z方向上的分量分别由蓝色，绿色，红色曲线表示，总速度由粉色曲线表示); (e) 平行/垂直于磁场方向的离子温度 (平行温度由蓝色曲线表示，垂直温度 由红色 曲线表示).Fig.1 Identifying crossing events by plotting (a) Ion energy flux; (b) The ion number density; (c) The magnetic field in GSE coordinates (The component of the magnetic field in the x direction is represented by the blue curve, and the y direction is green, the z direction is red); (d) The ion velocity in GSE coordinates (The component of the velocity in the x direction is represented by the blue curve, and the y direction is green, the z direction is red); (e) The ion temperature parallel/perpendicular to the magnetic field direction (The parallel temperature is shown by the blue curve and the vertical temperature is shown by the red curve).

随后，本文对筛选得到的穿越事件进行分析、计算、分类.对每个穿越事件，本文首先将磁场数据由GSE坐标系转化至局地坐标系中，并通过进一步分析确定了磁层顶区域以及卫星穿越磁层顶的时刻，这部分会在2.3节中加以说明.而后采用MFR法(法拉第残差最小化分析法)，计算了磁层顶的法向方向以及法向方向上的磁层顶运动速度，并且用HT分析法(DeHoffmann-Teller分析法)结合带约束的最小方差分析(MVABC)法，对上述参数的准确性进行了验证.随后，本文进一步计算了磁层顶的厚度及其电流密度.最后，收集了上游鞘区的β值，并对磁层顶的旋转不连续和切向不连续进行分类.下面将对这些参数的计算方法进行详细介绍.

1.3 磁层顶区域以及穿越时刻的确定

对于磁层顶区域的确定，早期研究有的用等离子体密度的跳变作为判断依据，而有的则应用磁场的跳变作为参考.Harris(1962)提出了一维哈里斯电流片法，该方法用最大磁场跳变的76%来定义电流片的位置和厚度，并在之后的研究中得到了众人的广泛应用，本文采用该方法对磁层顶进行判定和计算.

1.3.1 LMN坐标系的转化

本文首先根据前一部分筛选出的各穿越事件的低分辨率磁场数据，构建局地正交LMN坐标系(Russell and Elphic，1978).本研究中，该坐标系主要通过最小方差分析法(MVAB)(Sonnerup and Scheible，1998)构建，首先应用5 min研究时段内的低分辨率磁场数据构建矩阵：

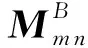
首先，定义LMN坐标系的L轴平行于x1向量，并使得L轴的ZGSE分量为正.一般情况下，在磁层顶附近，最大方差方向很大程度上取决于磁层磁场的方向，因而L轴的确定较为容易且相对准确，由于本研究在这部分主要关心L方向上的分量，因此该方法与研究目标较为契合.随后，定义坐标系的N轴平行于x3向量，类似的，使得N轴XGSE分量为正.理想情况下，N轴应该垂直于磁层顶电流片，但在本研究中，首先，本次MVAB计算选取的是全时段5 min的数据，时间跨度过大；其次，特征值λ2和λ3存在差别不大的情况，这就可能导致最小方差方向不能很好地表示磁层顶电流片法向，因而，磁层顶电流片法向的确定还需用其他方法加以计算，这在之后的3.3节会加以说明.最后，由右手定则，确定正交坐标系的M轴.将高分辨率磁场由GSE坐标系转化至LMN坐标系中，再对各穿越事件5 min时段内的磁场分量BL的突变的大致时段进行自动的查找和定位.

1.3.2 磁场突变研究时段的自动查找

第一步，为了一定程度上消除电流片上小结构对磁场突变查找的影响，本文对高分辨率磁场L方向分量BL进行3 s平均的平滑处理.

第二步，参考前人有关磁层顶的研究，卫星穿越磁层顶的过程一般不会维持很长的时间，因此本文设定一个30 s时长的滑动窗口，对5 min时段内的BL数据进行检查，找到30 s内平均变化率绝对值最大的时段，以该时段为中心，向前回溯30 s，向后推迟30 s，这样就得到了时长为1 min 30 s的时段，定义该时段为磁场突变研究时段ttmut1.

值得注意的是，有些事件的ttmut1可能超出了原有的5 min时段的范围，对于这样的事件，本文将ttmut1超出范围的起/止时刻强制定义为原有5 min时段的起/止时刻，并作出标记，留待后续处理.随后，在ttmut1中进行磁层顶区域以及卫星穿越时刻的确认.

1.3.3 磁层顶区域起始时刻和穿越时刻的确定

第一步，找到ttmut1中的最大BL值BL-max和最小BL值BL-min，将这两个值所对应的时刻tmax和tmin作为磁场跃变的起止时刻，两时刻之间的时段定义为跃变时段ttmut2.

第二步，找到ttmut2中BL值达到跃变的50%，即0.5(BL-max+BL-min)的点所对应的时刻，我们定义该时刻为卫星的穿越时刻t50，该时刻卫星所处的位置定义为穿越位置posc.值得注意的是，在实际操作中可能出现多个时刻均满足这个条件的情况，本文中，对所有类似情况均选择最靠前的一个时刻作为穿越时刻.

第三步，类似于t50的确定，找到ttmut2中BL值达到跃变的12%和88%的点所对应的时刻t12和t88，作为磁层顶区域的起止时刻.类似地，对同时多个时刻满足条件的情况，均选取最靠前的时刻作为对应时刻.定义t12和t88之间的时段为ttmap，该时段时长定义为穿越时长tcr，并认为在该时段内卫星处于磁层顶区域.下面将提出一个例子进行说明.

1.3.4 2002年1月16日的磁层顶穿越事件

如图2所示，在该时段内，卫星穿越了磁层顶，但是离子数密度突然增高(图2b)，离子温度突然降低(图2e)，各能级离子通量突然变化(图2a)，以及磁场(图2c)和离子速度(图2d)方向和大小的跳变均发生在00∶31∶10附近，实际的穿越时刻明显与原列表中给出的卫星于00∶30穿越磁层顶有所偏移，因此有必要对其穿越时刻进行进一步的定位.与此同时，将磁场和离子速度参数转换至LMN坐标系后，其参数的突变变得更为明显，有利于我们定位突变的位置，从而进一步确定磁层顶穿越时刻及磁层顶区域.

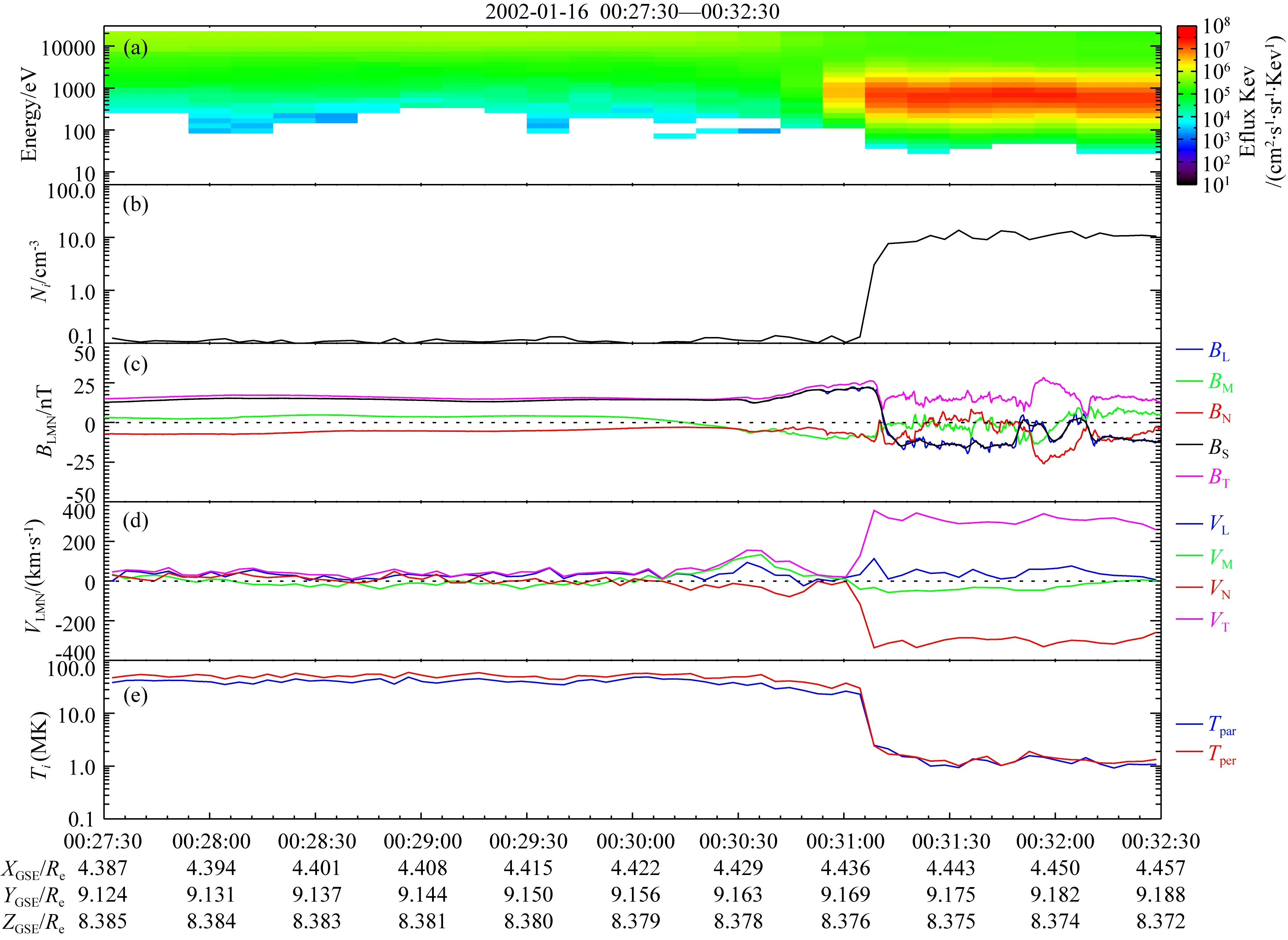
图2 2002年1月16日的磁层顶穿越事件 (a) 离子能量通量; (b) 离子数密度; (c) LMN坐标系下的磁场三份量(磁场L方向分量由蓝色曲线表示，M方向分量由绿色曲线表示，N方向分量由红色曲线表示，BL分量3 s平滑处理后的结果由黑色曲线表示，总磁场由粉色曲线表示); (d) LMN坐标系下的离子速度三份量(L、M、N方向分量分别由蓝色、绿色、红色表示，总速度由粉色曲线表示); (e) 平行/垂直于磁场方向的离子温度(平行温度由蓝色 曲线表示，垂直温度由红色曲线表示).Fig.2 A crossing event, which occurred on January 16, 2002 (a) Ion energy flux; (b) The ion number density; (c) The magnetic field in LMN coordinates (The component of the magnetic field in the L direction is represented by the blue curve, and the M direction is green, the N direction is red, the total value is pink, and the solid black line in the magnetic field map is the magnetic field BL component data after 3-s smoothing); (d) The ion velocity in LMN coordinates (The component of the velocity in the L, M, N direction is represented by the blue, green, red curve, and the total value is represented by the pink curve); (e) The ion temperature parallel/perpendicular to the magnetic field direction (The parallel temperature is shown by the blue curve and the vertical temperature is shown by the red curve).

图3表示的是高分辨率磁场数据在LMN坐标系下的三分量，其中黑色曲线代表磁场BL分量经过3 s平滑后的情况.两条红色竖虚线之间的部分，为程序自动查找的时长为30 s的BL变化最大时段. 前后各推30s，得到了绿色竖虚线所夹的磁场突变研究时段ttmut1.在该研究时段内，找到黑色横虚线所示的BL分量最大值和最小值.蓝色竖向点划线分别标出了BL分量达到突变值88%和12%的时刻，这两个时刻就是磁层顶区域的起止时刻，黑色竖向点划线标出了BL分量达到突变值50%的穿越时刻.在该事件中，穿越时刻大致为00∶31∶11，对应的卫星位置为[4.438,9.171,8.375](Re)，卫星穿越磁层顶区域花费时间约为12.8 s.

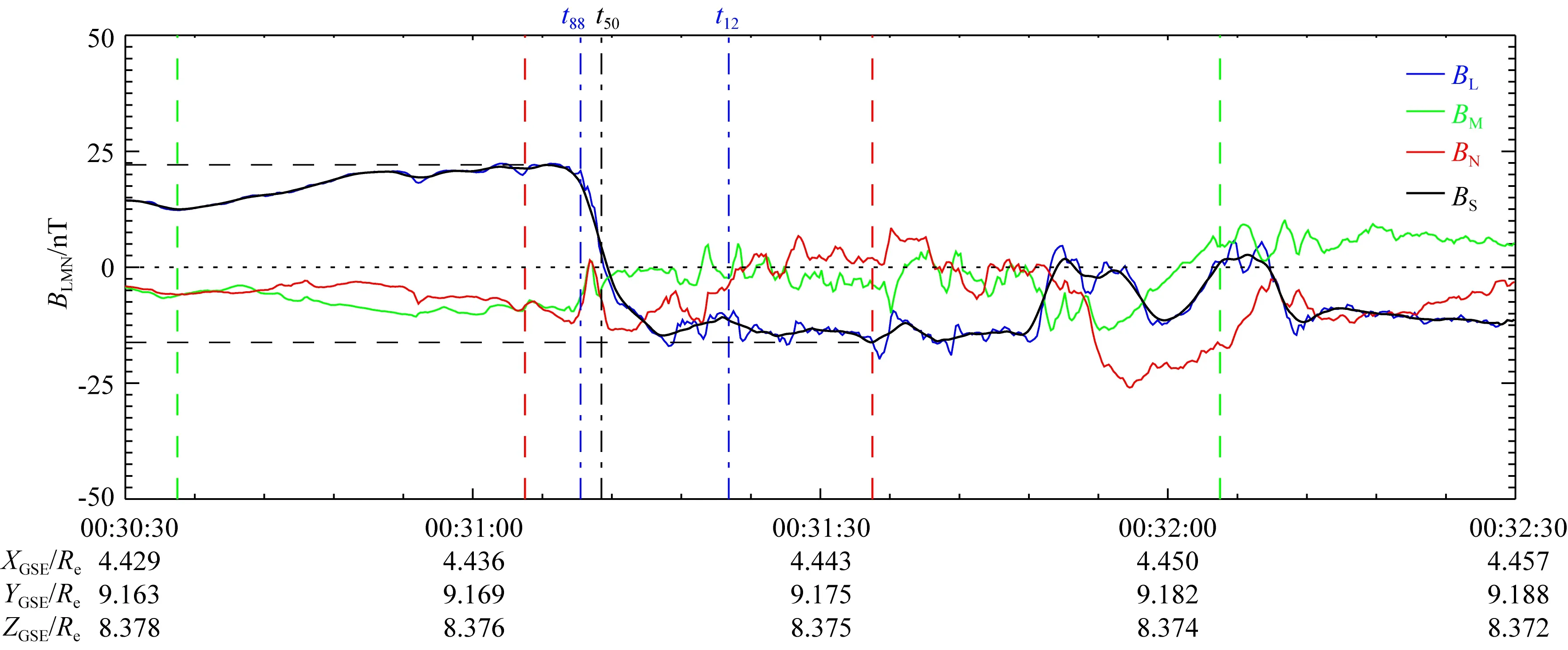
图3 2002年1月16日的穿越事件中，确定卫星穿越时刻以及磁层顶区域的示意图Fig.3 Determine the time (Crossing time; The time when the satellite was in the region of the magnetopause) of the crossing event occurring on 16 January 2002

1.4 磁层顶运动速度、厚度、电流密度的计算

计算磁层顶运动速度、厚度、电流密度时，要定义用于计算这些量的时段.本文以ttmap时段为中心，向前回溯tcr，到达时刻tcalf，向后推迟tcr，到达时刻tcall，得到tcalf和tcall之间三倍于穿越时长tcr的时段，将该时段定义为计算时段ttcal，随后利用该时段内GSE坐标下的数据，对磁层顶大尺度特征进行计算.

磁层顶电流片的法相方向以及在其方向上的磁层顶运动速度主要使用MFR法进行计算.作为对比，本文也应用HT法结合MVABC法对这两个参量进行计算.随后根据计算结果，可以进一步推出磁层顶的厚度.最后利用简化的安培定律计算磁层顶电流片的平均电流密度.

1.4.1 MFR法计算磁层顶电流片法向和运动速度

MFR方法通过计算电流片及其附近上下游区域的电场和磁场，可以返回一个参考系，在该参考系中，切向电场最小，同时可以给出该参考系的运动速度的大小，在本研究中，参考系的速度就是磁层顶电流片在其法向上的运动速度.类似于MVAB方法，MFR方法同样返回一组特征值，对应返回一组特征向量.在本研究中，特征向量可以用于估算磁层顶电流片的法向nFMR，特征值可以用于估算计算结果的质量.Khrabrov和Sonnerup(1998)的文章中有对该方法原理的详细说明，下面仅叙述具体的计算步骤.

第一步，计算ttcal时段内的平均磁场〈Bk〉和平均电场〈Ek〉.这里的电场数据E由对应时刻的离子运动速度Vi和高分辨率磁场B计算得出，即E=Vi×B，下标k表示数据点的编号.由于Vi和B的分辨率不同，对B进行插值处理以适应Vi的分辨率.

第二步，计算δEk=Ek-〈Ek〉以及δBk=Bk-〈Bk〉.

第四步，计算向量P=〈δEk×δBk〉.

至此，就得到了前文所述的MVAB方法类似的3×3的矩阵Q，对该矩阵同样可得出三个由大到小排列的特征值λ1、λ2和λ3，最小特征值λ3对应的特征向量即作为本研究中的磁层顶电流片的法向nMFR，这里需要使得该向量的XGSE分量为正，即一般情况下指向磁层顶的外侧.值得注意的是，特征参量λ2和λ3的差异指示了磁层顶电流片法向nFMR的质量，在本研究中，去除了两特征量差别不大，即λ2/λ3小于2的事件.

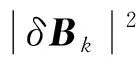
值得注意的是，为保证采样数据不至于过少，我们只保留ttcal时段内至少有五个采样数据的事件，同时也去除了ttcal时段内存在必要数据缺失的事件.

1.4.2 HT分析计算磁层顶电流片法向和运动速度

本文同时应用HT分析法，对MFR法可用的各穿越事件中，磁层顶电流片的法向及其法向方向上的运动速度进行计算，其计算结果留待最后的统计部分与MFR的结果进行对比分析，统计分析以MFR法的计算结果为主.在这部分用于计算的时段与MFR法所用的时段相同，其主要步骤为，首先应用HT法确定一个参考系，并计算该参考系(本研究中为磁层顶电流片)的运动速度向量，随后应用带约束的最小方差分析法(MVABC)得到的磁层顶法向向量，两向量点乘，即可得到最终的磁层顶电流片法向速度.

HT法的原理在Paschmann和Sonnerup(2008)一文中有详细说明，这里只列出运算步骤，磁层顶电流片在其穿越位置的整体运动速度可由下列矩阵得出：

其中B是磁场，下标x、y和z表示在GSE坐标系下沿三个坐标轴方向的分量.电场E同样由离子速度和磁场计算得到，最后可得运动速度向量Vfr=(Vx,Vy,Vz)，之后计算磁层顶法向.

前文已经提及，应用MVAB法在特征值λ2≃λ3情况下得到的法向量预测可能存在问题.MVABC通过约束条件〈B〉·nMVABC=0，对MVAB得到的结果进行进一步的修正，其中B为计算时段内的磁场向量，nMVABC为通过该方法最终得到的法向量.MVABC的原理及推导过程在Sonnerup和Scheible(1998)的文章中有详细叙述，在这里仅说明其计算步骤.

第一步，应用MVAB法，对ttcal时段内的高分辨率磁场数据进行计算，得到由大到小排列的特征参数λ1、λ2和λ3，以及对应的特征向量x1、x2和x3.

第二步，将ttcal时段内各时刻的高分辨磁场数据沿x1、x2和x3的方向重新拆分成三分量B1k、B2k和B3k，下标k表示ttcal时段内数据点的编号.

第三步，解下列关于λ的方程可以得到两个由大到小排列的根λmax和λmin.

第四步，计算

第五步，计算

ni=Γ〈Bi〉/(λi-λmin),

其中i=1,2,3，至此得出了nMVABC沿x1、x2和x3方向的分量.

第六步，nMVABC由下面公式求得

nMVABC=n1x1+n2x2+n3x3.

类似地，我们强制nMVABC的XGSE分量为正，保证大部分情况下法向方向指向磁层顶外侧.

最后，得到磁层顶法向分量的运动速度的大小VHT=Vfr·nMVABC.

1.4.3 磁层顶电流片厚度以及电流密度的计算

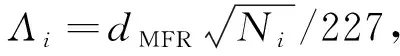
在已知电流片厚度的情况下，应用一维安培定律，电流片的平均电流密度J可由电流片两端磁场的跳变值计算得到，具体公式为μ0J=ΔB/d.在本研究中，我们将磁场跳变ΔB近似地记为电流片两端BL分量的变化，两端的取值点选在t12和t88时刻.

1.5 穿越事件的进一步筛选以及卫星穿越方向的判断

前文中确定了磁层顶区域以及计算时段，如图3，我们将每个事件的磁层顶区域和计算时段的起止时刻都用虚线标注，随后，检查所有穿越事件的数据.由于本文是自动检测磁场突变区，进而定位磁层顶区域，不可避免地会因为各种实际问题出现定位不准的情况.尤其是磁鞘区域在一些情况下湍动强烈，可能导致最大突变区出现在磁鞘区.因而在这部分，本文再次结合离子能量通量、密度、速度等参量，对磁层顶区域的定位进行人工筛查，去除了定位明显不合理的事件.另外，为了保证相对准确，去除了BL在磁层顶两侧变化小于10 nT的事件.

同时，原穿越列表存在两个穿越事件给出的穿越时间极为相近的情况，这就可能出现:

(1)不同的穿越事件定位到相同的磁层顶区，本文针对这种情况也在这部分进行了去重复操作；

(2)卫星发生连续且短暂的穿越，磁层顶区定位虽然不同但计算时段发生重叠，本文对这种情况仅选取一个穿越事件作为一段时间内连续穿越的代表，或者去除该段时间内所有的穿越事件.

在这部分，本文也结合离子能量通量以及离子密度等数据，对磁鞘区和磁层区进行了简单的划分，即磁鞘区域的离子较之磁层区域的离子密度更高，温度更低.并以此为依据，记录了卫星在本次磁层顶穿越事件中的穿越方向，将tcalf和tcall这两个时刻卫星在磁鞘侧的时刻定义为tcalu，在磁层侧的时刻定义为tcald.

1.6 旋转不连续和切向不连续的判定以及上游β参数的收集

磁层顶在流体理论中可以分为切向不连续(TD)和旋转不连续(RD)(Hudson，1970).理想的TD意味着磁层顶两侧，即磁鞘侧和磁层侧的等离子体状态，包括运动速度、温度等参量完全分离.磁层顶电流片作为边界层可以整体运动，与此同时，两侧的等离子体不会发生越过边界层的输运和传递，磁层顶法向方向上的磁场分量为零.与之相对的，磁层顶在RD状态的情况下，磁层和磁鞘两区域的等离子体之间可以实现越过边界层的输运和能量交换，磁场在磁层顶法向方向上的分量可能不为零，该状态指示磁场重联，这一可实现磁鞘和磁层物质能量交换的重要物理过程可能存在.

对于TD和RD的分类，一般通过分析穿过磁层顶的上下游之间，等离子体速度变化和局地阿尔芬速度变化之间的比例关系进行定量说明，即

ΔV=±ΔVA.

由于理想TD的状态下两侧等离子体的“完全分离”，该等式不成立，而RD情况下两侧磁场及附在其上的等离子体发生耦合，因而结果与TD相反.这种两个速度参数变化的对比分析称为瓦伦关系测试，该方法的原理在Walén(1944)中有详细说明.可以发现，两个向量的对比包括方向的对比和大小的对比，Sonnerup等(2018)应用指示参数Q对两向量的一致性进行说明，本文仿照该方法进行计算.下面将叙述瓦伦测试的具体计算步骤以及分类标准，并给出一个实际的例子加以说明.

1.6.1 瓦伦测试及分类标准

第一步，选择tcalu时刻作为上游采样点，读取该时刻对应的离子速度为Viu，离子密度niu，平行于磁场的离子温度T∥u，垂直于磁场的离子温度T⊥u以及磁场Bu.

第二步，将磁层顶区域内所有数据点的离子速度与Viu做差，找出|ΔVi|最大的数据点，该点对应的时刻记为tmaxΔV，并仿照上游采样点，读取该时刻处卫星测得的离子各参数和磁场数据，记录ΔVi.

第三步，计算两个采样点处的平行热压p∥=nikT∥，垂直热压p⊥=nikT⊥，其中k为玻尔兹曼常数.

第四步，计算两个采样点处阿尔芬速度VA，公式为

VA=B[(1-α)/μ0ρ]0.5,

其中，α=(p∥-p⊥)μ0/B2，ρ为离子质量密度，本研究中假定这里的离子均为质子，于是得到ρ=mpni，其中mp为质子质量.

第五步，将两采样点处的阿尔芬速度做差，得到ΔVA，若磁场与等离子体速度法向分量符号相同，则该值不变，若符号相反，则该值前加一个负号.

第六步，引入指示参数Q，计算ΔVA和ΔVi的一致性，具体公式如下：

这里，Q是一个值域为[-1,+1]的数，其正负号指示应用于重联的不同区域，这在Sonnerup等(2018)中有明确说明，在本研究中，不考虑应用的区域，因此对Q取绝对值.本文仿照Haaland等(2019)的标准，以0.5为阈值，当穿越事件的|Q|值大于等于0.5时，判定磁层顶为RD，小于0.5时为TD.

1.6.2 近磁层顶区域磁鞘侧β的收集

粒子热压与磁压之比为β，是表述局地等离子体状态的一个重要参数.本文将t12和t88两时刻中更接近磁鞘区的时刻作为采样点，读取了各穿越事件在该时刻采集到的参数，计算了温度各向异性T∥/T⊥和β值，具体公式如下：

β=pT/pB,

其中，pT是离子热压，pB是磁压(pB=B2/2μ0，B是采样时刻的磁场，μ0是真空介电常数).经计算，发现在各穿越事件中，温度的各向异性并不明显，因此在所有计算中都采用平行于磁场的离子温度T∥近似计算得到pT=nikT∥(ni是采样时刻的离子数密度，k是玻尔兹曼常量).

1.6.3 2001年12月3日的磁层顶穿越事件

如图4，这里给出了C3卫星于2001年12月3日发生的磁层顶穿越事件的例子，红色竖直点划线标出计算时段ttcal起止时刻tcalf和tcall，蓝色竖直点划线为卫星穿过磁层顶区域的起止时刻，黑色点划线为我们定义的卫星穿越时刻.可以看出，卫星在磁层顶附近观测到磁场反转同时伴随离子高速流，这些也是卫星经过重联区域的典型现象.

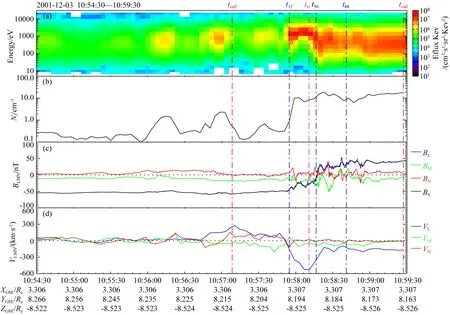
图4 一个穿越旋转不连续磁层顶的例子，发生于2001年12月3日的磁层顶穿越事件 红色竖直点划线标出计算时段t tcal起止时刻tcalf和tcall，蓝色竖直点划线为卫星穿过磁层顶区域的起止时刻， 黑色竖直点划线为我们定义的卫星穿越时刻，粉色竖直点划线为速度变化最大时刻.Fig.4 An example of crossing events, which is rotation discontinuity, occurred on 3 December 2001 The vertical dots in red indicate the start and end times tcalf and tcall of the calculation period t tcal, the vertical dots in blue indicate the start and end times of the satellite crossing the magnetopause region, the vertical dots in black indicate the time of the satellite crossing, and the vertical dots in pink indicate the time when the changing of the velocity is maximum.

本事件中，我们选取tcall时刻作为磁鞘区域的采样点来进行瓦伦测试的相关计算.黄色竖直点划线对应时刻为磁层顶区域内相对tcall时刻，是速度变化最大的时刻.同时，选取t88作为该事件β值的采样点.

经计算，在该事件中，磁层顶法向方向nMFR≈[0.73,0.35,-0.56]，nMVABC≈[0.78,0.41,-0.47]法向方向上的运动速度VMFR≈-4.10 km·s-1，VHT≈11.58 km·s-1.卫星穿越时长tcr≈46.20 s，磁层顶厚度dMFR≈189.53 km，Λi≈2.47，近磁层顶磁鞘侧热压磁压比β≈0.49，平均电流密度J≈329 nA·m-2.瓦伦测试指示参数|Q|≈0.86，说明磁层顶处于旋转不连续的状态，进一步佐证重联发生的可能.可以看出，两种方法计算得到的磁层顶运动速度存在一定差异，甚至方向都发生了反转，但是值得注意的是，两个结果的绝对值都不大，即磁层顶可能正处于相对稳定的状态，同时，旋转不连续也可能是造成两种方法结果不同的原因.

2 结果与分析

在上一部分中，本文对Karlheinz Trattner, Steven Petrinec和Stephen Fuselier提供C3卫星2001年到2009年的磁层顶穿越列表进行了再筛选，具体的筛选标准总结如下：

(1)选取在5 min研究时段内参数能明显反映卫星发生穿越的事件；

(2)去除磁层顶区域自动定位不准的事件；

(3)去除重复事件及计算时段重叠的部分事件；

(4)去除MFR计算中λ2/λ3小于2的事件；

(5)去除BL分量在穿越前后变化不足10 nT的事件；

(6)仅保留磁层顶厚度在150～10000 km范围内的事件；

(7)因本研究集中在低纬区域，仅保留穿越位置在GSE坐标系下纬度在45°范围内的事件.

总共得到了1139个满足条件的事件.随后，将这些事件按穿越位置posc所在的磁地方时MLT进行划分，MLT≥16的区域为昏侧区域，MLT≤8的区域为晨侧区域，16>MLT>8范围内的区域为日侧区域.在晨侧有548个穿越事件，昏侧有322个事件，日侧有269个事件，所有事件在GSE坐标系下X-Y面上的分布图如图5所示.

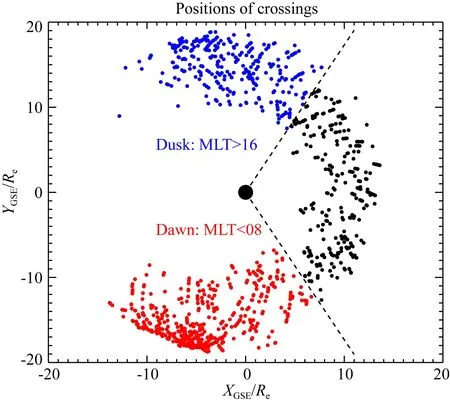
图5 磁层顶穿越位置投影至GSE坐标系下 X-Y面上的分布图 其中红点为晨侧穿越事件的穿越位置分布，蓝点为昏侧， 黑点为日侧，虚线标明了晨昏分界线.Fig.5 The crossing locations which are projected to the distribution map on the X-Y plane in the GSE coordinate system Where the red dot is the crossing location distribution of the dawn side crossing event, the blue dot is the dusk side, the black dot is the dayside, and the dotted line indicates the dividing line between dawn and dusk.

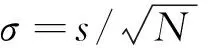
将前文计算得到的磁层顶运动速度绝对值、磁层顶厚度、电流密度以及上游β值等参量进行统计，结果如表1所示.

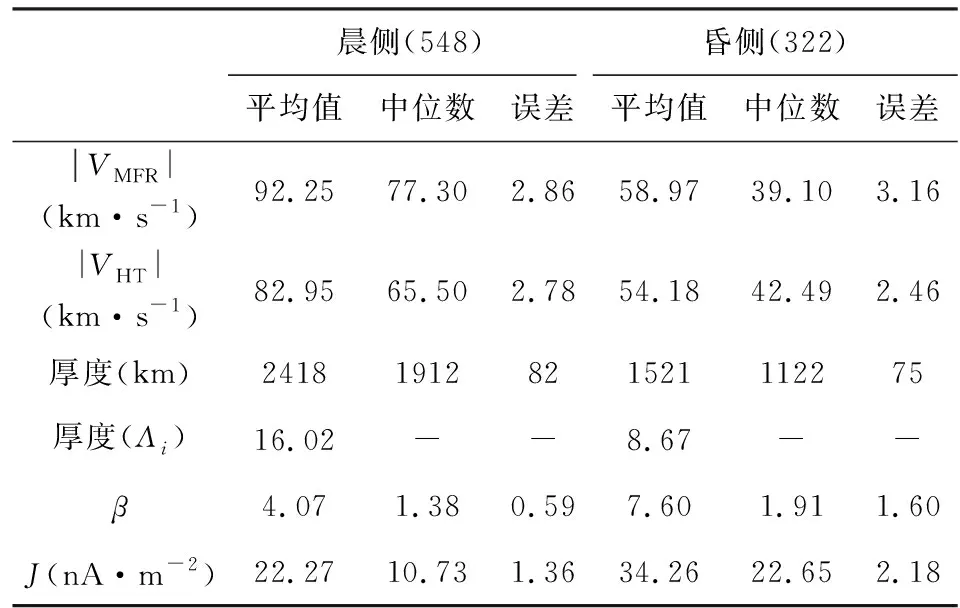
表1 基于Cluster C3卫星数据的磁层顶主要参数Table1 Key magnetopause parameters based on Cluster C3

2.1 磁层顶运动、电流密度及其厚度

从表1可以看出，磁层顶的厚度、运动速度以及电流密度在晨昏两侧存在明显的不对称.即

(1)晨侧磁层顶电流片的厚度更厚，从离子惯性尺度表征的磁层顶厚度来看，晨侧磁层顶的厚度甚至接近达到了昏侧的二倍；

(2)晨侧磁层顶电流片在其法向方向上的运动较之昏侧更为活跃；

(3)晨侧磁层顶电流片的电流密度较之昏侧的更小.

在将晨昏两侧磁层顶电流片电流密度的平均值和厚度相乘后得到了大致相等的值，这可以一定程度上说明磁层顶区域整体电流守恒.值得注意的是，本研究中两种方法计算得出的磁层顶运动速度的统计结果大致相当的，但与之前其他研究的结果相比(Haaland et al.，2014)，晨侧磁层顶的运动速度更大，相应的厚度也更厚，这可能是由穿越事件的选择以及计算方法的不同导致的.

本文将磁层顶晨昏两侧，按类似于磁地方时的方法，以其穿越时刻卫星位置到正午的角度，每15°一个扇区进行分区，给出了磁层顶晨昏两侧区域的厚度和速度在其各扇区内的中值和平均值，角度越大，表示越接近磁尾.

如图6，纵坐标为取绝对值后的磁层顶运动速度，横坐标为各事件中发生磁层顶穿越的位置到正午的角度，虚线和实线分别表示晨侧磁层顶运动速度绝对值在各分区的中位数和平均数，点虚线和点划线分别表示昏侧磁层顶运动速度绝对值在各分区的中位数和平均数，横坐标每15°分一个扇区进行统计.

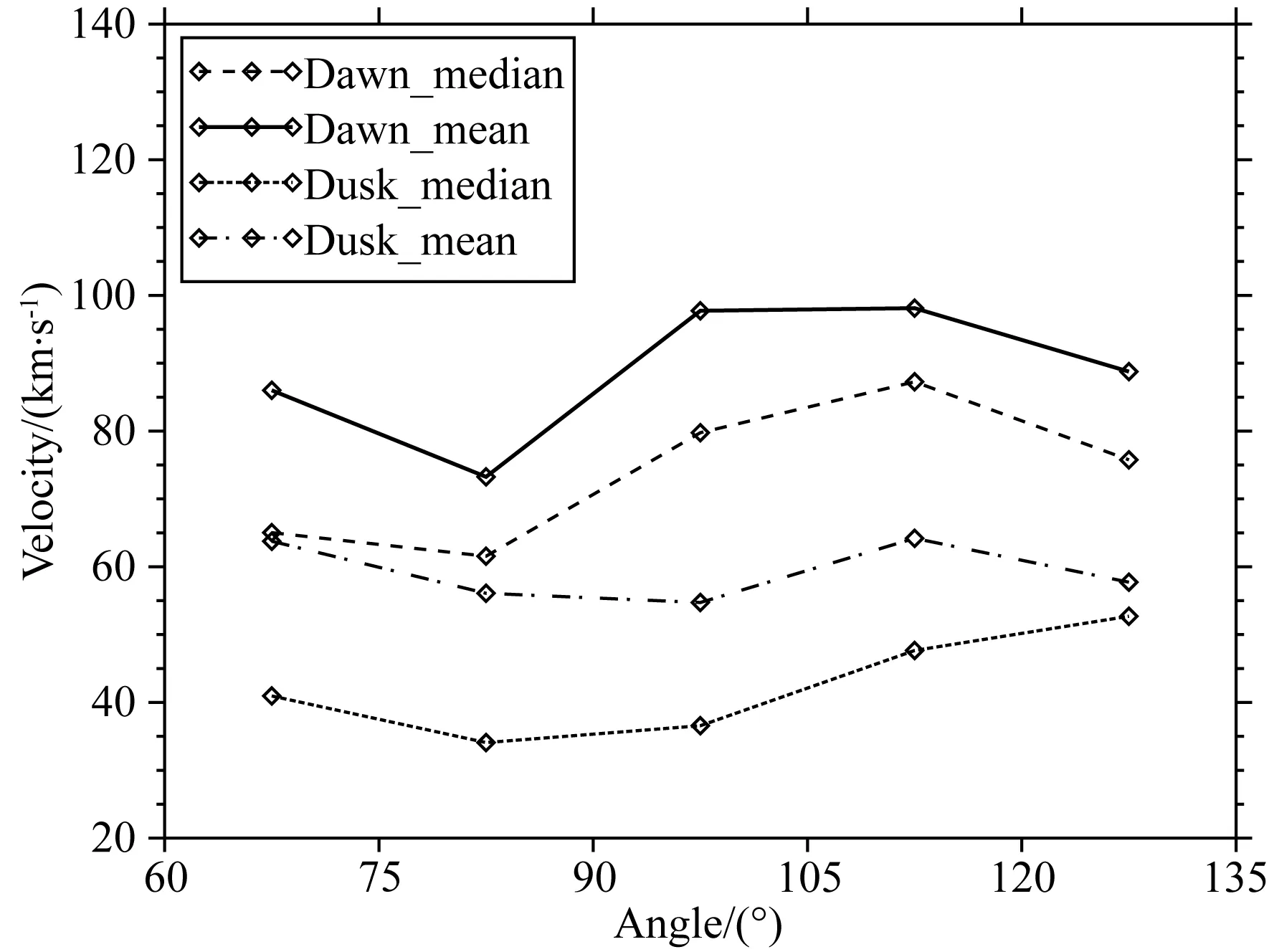
图6 磁层顶运动速度分布图Fig.6 Distribution of magnetopause motions

图7的横坐标与图6类似，纵坐标为计算得到的磁层顶厚度.由图6和图7可以看出，磁层顶的一些特征参数存在明显的晨昏不对称，无论速度还是厚度，晨昏两侧的统计结果均表现出明显的分离，具体的不对称情况将在2.3节中进行详细的分析和说明.与此同时，由近日侧到磁尾，磁层顶的运动速度在晨昏两侧在整体上都表现出上升趋势，且在近日侧区域就展现出较大的差别.磁层顶电流片的厚度由近日侧到尾部也呈上升趋势，在近日侧区域，晨昏两侧磁层顶厚度差别不大.

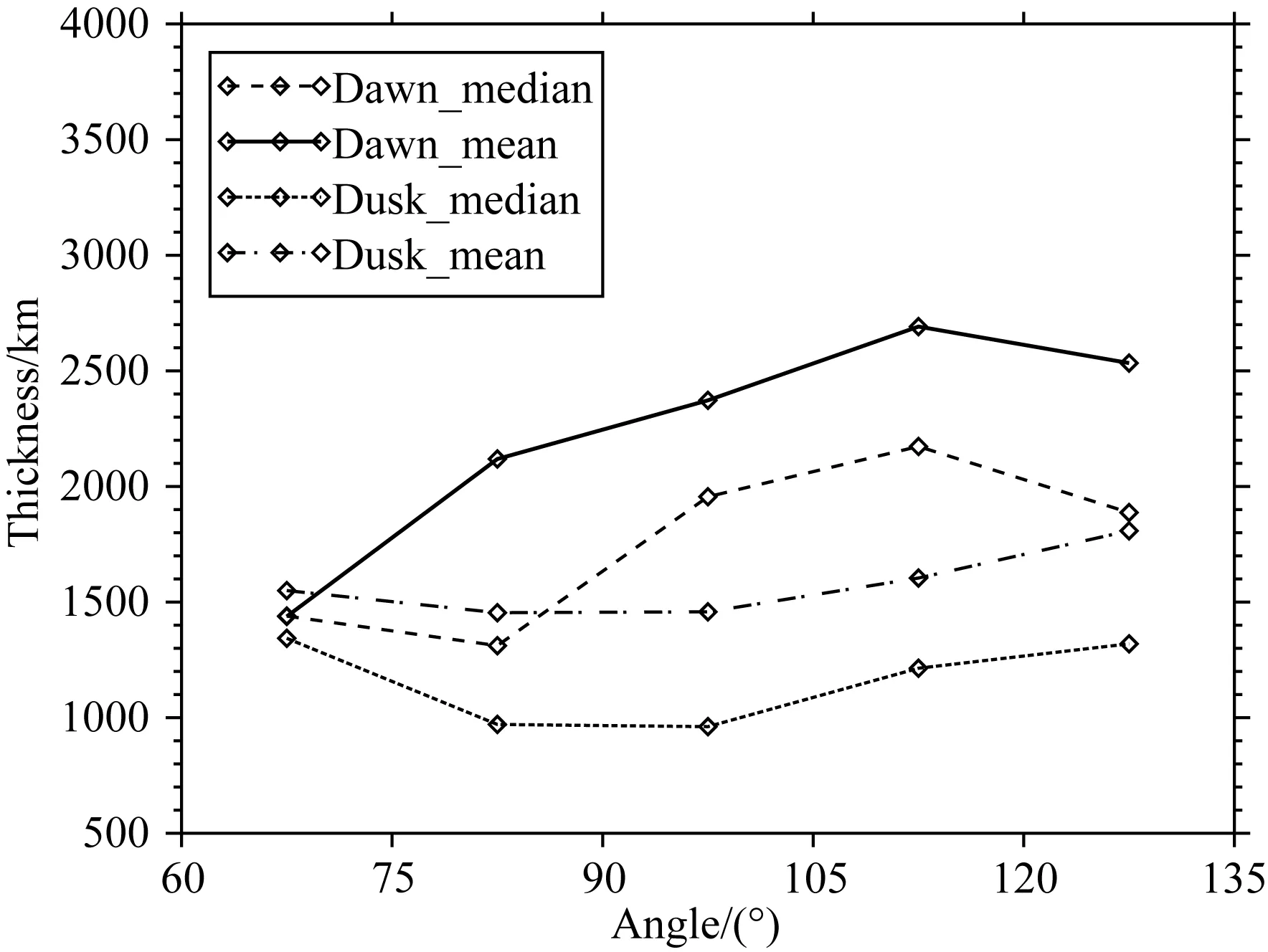
图7 磁层顶厚度的分布图Fig.7 Distribution of magnetopause thickness

2.2 磁层顶磁鞘侧β值情况

由表1可以发现磁层顶磁鞘侧的β也存在晨昏不对称，晨侧的上游β值要小于昏侧的上游β值.本文统计了晨昏两侧β的分布，结果如下图所示.

如图8, 灰色条带代表晨侧结果，黑色条带代表昏侧结果，横坐标为上游β值，纵坐标为占对应数据集的百分比.结果表明，晨昏两侧的上游β值均集中在小于2的区域内，我们将β值小于2的事件定义为低β事件，将β值大于2的事件定义为高β事件.晨侧低β事件所占比例明显高于昏侧同类型事件占其总事件数的比例.同时，β值大于15的事件在晨昏两侧都不多见.

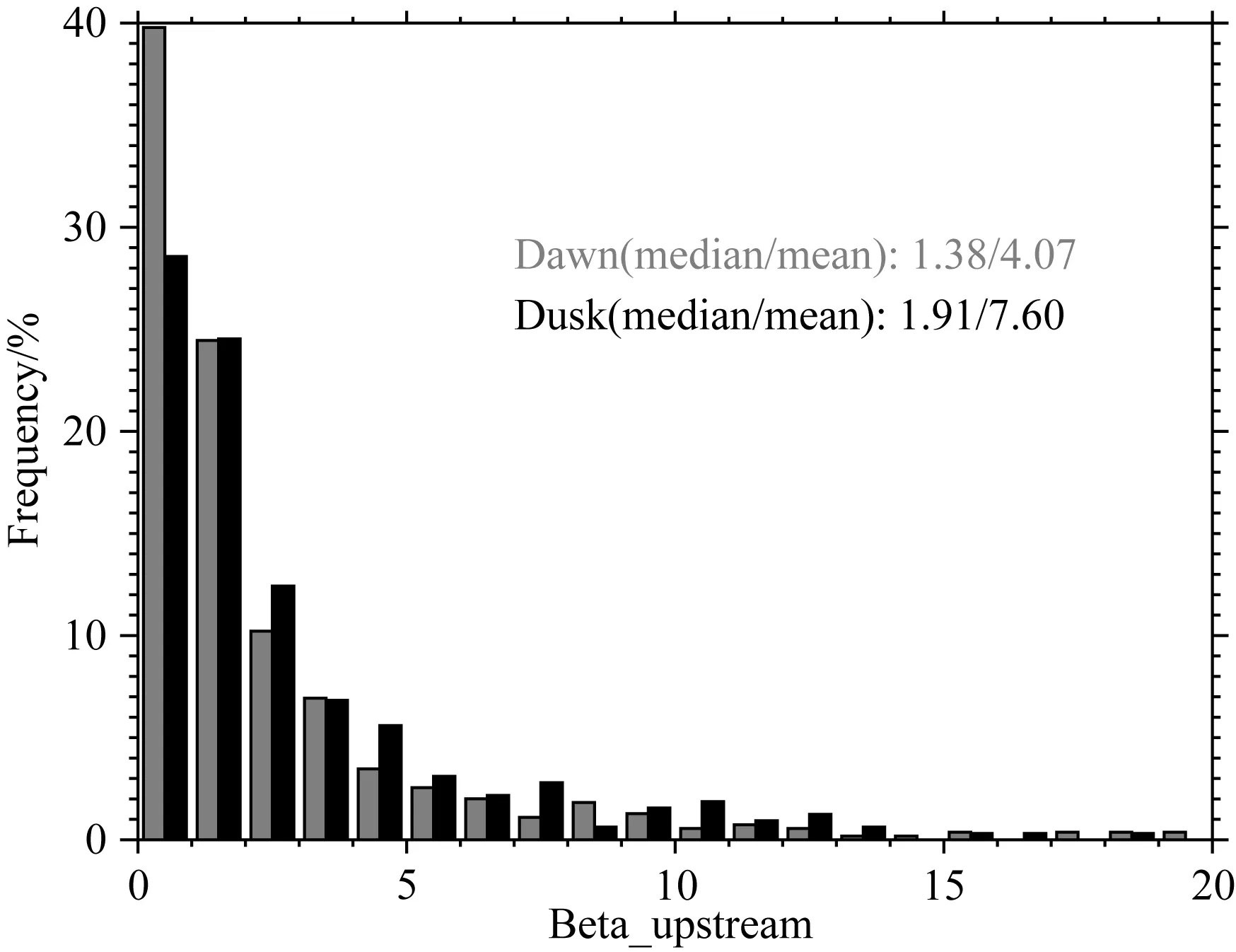
图8 上游β值的统计结果Fig.8 Statistical result of upstream β

类似于磁层顶的厚度和运动速度，如图9，本文也研究了磁层顶上游β值由近日侧到尾侧的数值情况，横坐标与图7的横坐标类似，纵坐标为上游β值，虚线为晨侧中值结果，点划线为昏侧中值结果.

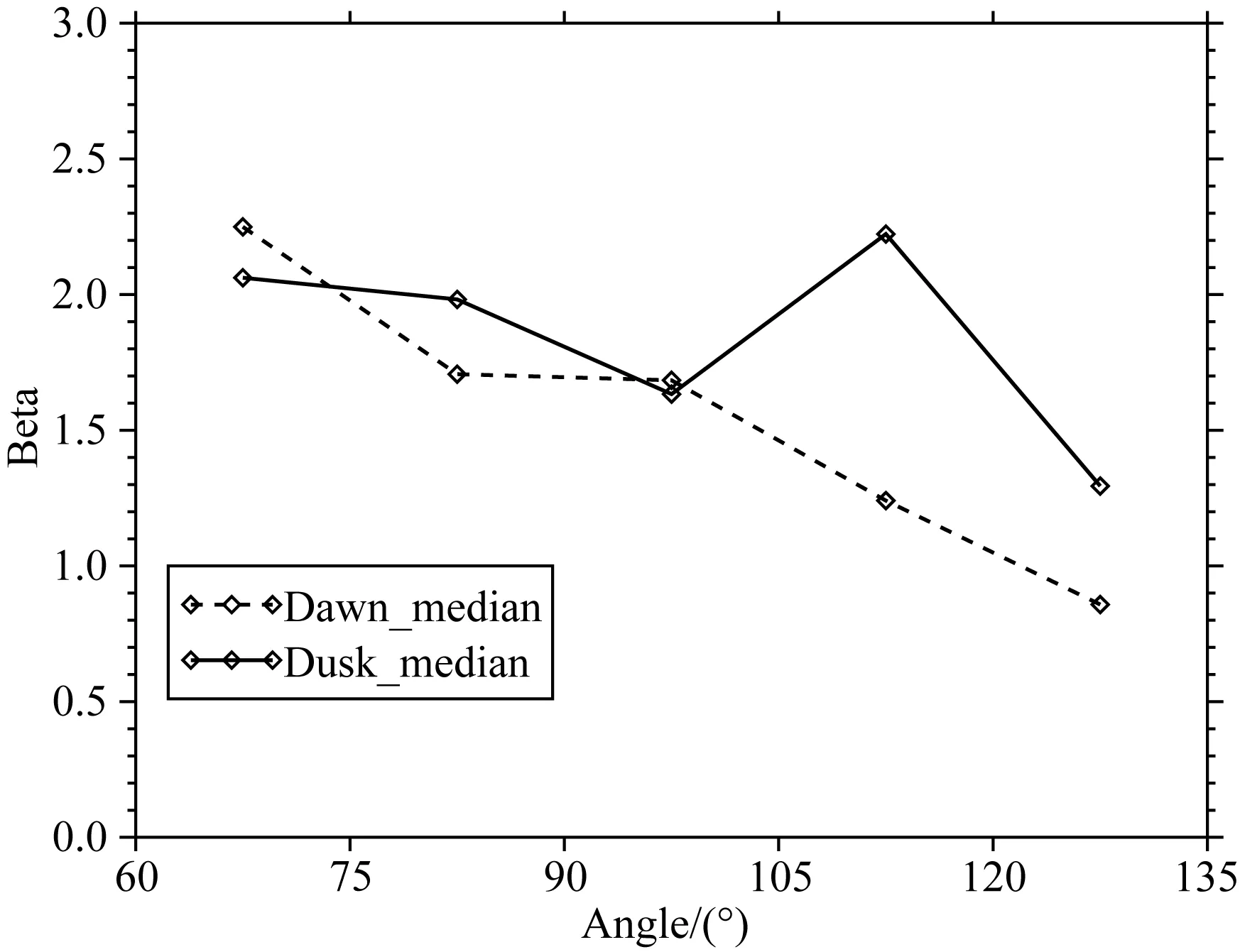
图9 上游β值分区统计结果Fig.9 Partitioned statistical result of upstream β

如前文提到的，由于β值一般都比较小，其均值受个别大值的影响较大，因此在这里仅用中值对β的分布进行表征.本文在这里发现了一个有意思的现象，虽然晨昏两侧β在整体趋势上都随着角度的变大而减小，即约接近尾部区域，β值越小，但是在昏侧的105°～120°扇区，β值出现了一个明显的跃升，具体原因有待进一步分析研究.

2.3 上游β与侧翼磁层顶参数的关系

这部分我们研究上游β对磁层顶侧翼特征参数，即磁层顶厚度和磁层顶运动速度的影响.由于晨昏两侧的特征参数存在不对称性，因而将它们分开进行研究和分析.如图10和图11所示，我们将事件分为高β值事件和低β值事件，画出了磁层顶厚度和运动速度的比重图.

如图10，横坐标代表磁层顶的厚度区间，每1000 km分一区，纵坐标是满足各区间厚度数值的事件占总事件数的比例.灰色条带是高β值事件的统计结果，黑色条带是低β值事件的统计结果.结果显示，高β值情况下，晨昏两侧的磁层顶厚度均展现出厚度小的情况占比提高，即β值更低，磁层顶厚度更大.这与Phan等(1996)提出的低纬日侧磁层顶厚度的结果一致.

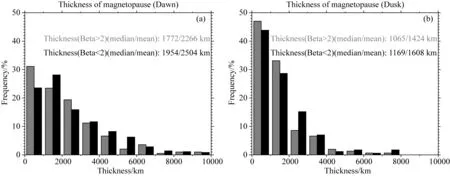
图10 上游β值对磁层顶厚度的影响 (a) 晨侧磁层顶的统计结果; (b) 昏侧磁层顶的统计结.Fig.10 Effect of upstream β values on magnetopause thickness (a) The result of the dawn side magnetopause; (b) The result of the dusk side magnetopause.

类似地，如图11，本文分析了上游β值对磁层顶侧翼运动速度的影响，结果表明，与低β值情况相比，高β值情况下，晨昏两侧的磁层顶速度均表现出速度小的情况占比提高，即β值更低，磁层顶运动速度更大.这与Phan等(1996)提出的低纬日侧区域，更高β值对应更高的磁层顶运动速度的结果相悖.

通过上述分析可以发现，上游β值与磁层顶侧翼的厚度和速度呈现出一定的相关性，晨侧磁层顶上游β值更小，而该区域的磁层顶运动速度更快，厚度更厚.为分析磁层顶的大尺度晨昏不对称是否是由上游β值造成的，本文对这三个参量由近日侧到尾侧的不对称进行了量化和表征.

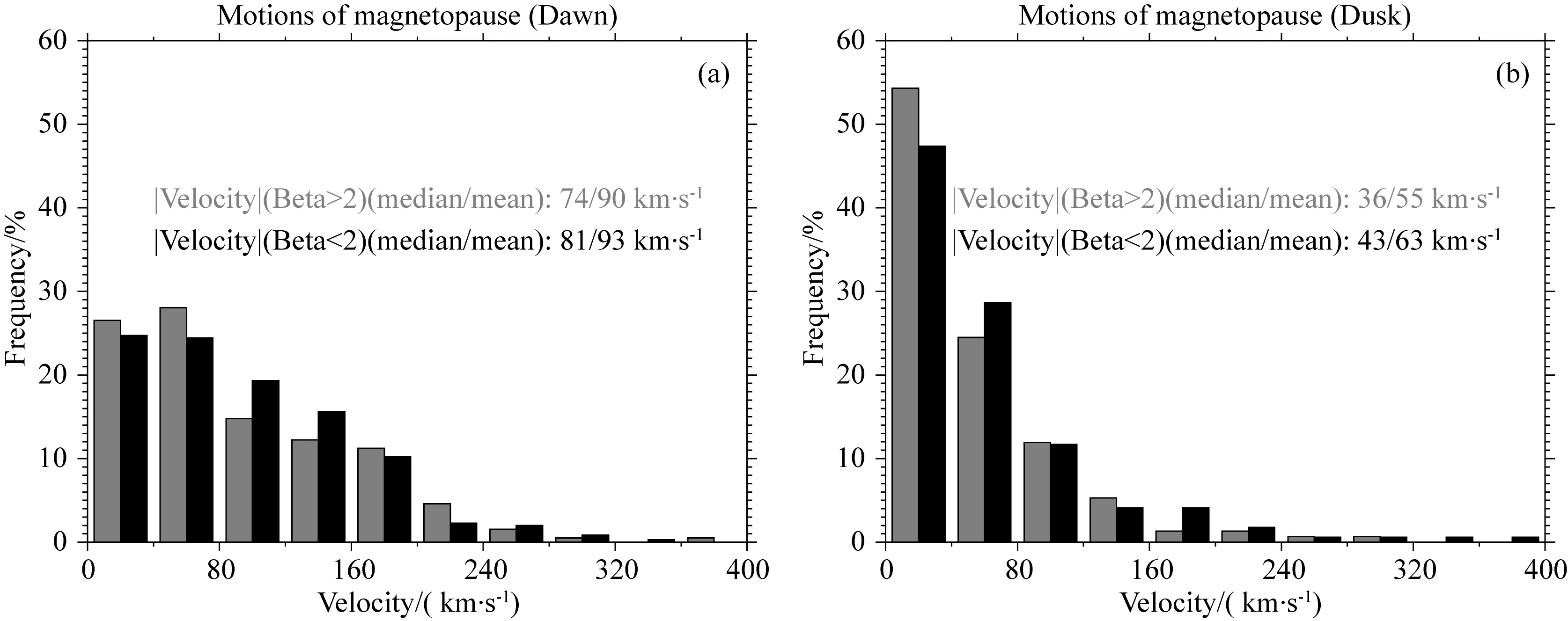
图11 上游β值对磁层顶运动速度的影响 (a) 晨侧的结果; (b) 昏侧的结果.Fig.11 Effect of upstream β values on magnetopause motions (a) The result of the dawn side magnetopause; (b) The result of the dusk side magnetopause.

如图12，横坐标是穿越位置到正午的角度分区，纵坐标是各参量的晨昏不对称度A，该值由下列公式计算得到：

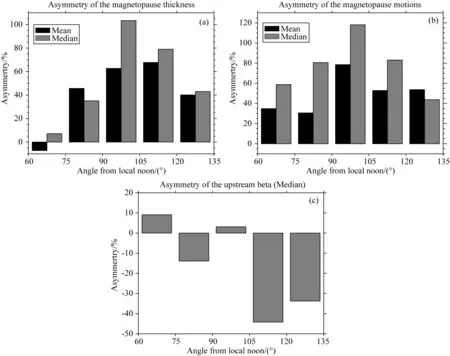
图12 参数晨昏不对称按位置的分布情况 (a) 磁层顶厚度不对称; (b) 运动速度不对称; (c) 上游β值不对称.Fig.12 The distribution of the dawn-dusk asymmetry of the parameters by position (a) Asymmetry of the magnetopause thickness; (b) Asymmetry of the magnetopause motions; (c) Asymmetry of the upstream β.

式中下标表示晨昏区，G表示某一参量在对应区域内的均值或中位数，灰色条带表明中位数，黑色条带表明平均数.A值绝对值的大小代表对应扇区的不对称程度，值越大，不对称越明显.若A大于0，则表明晨侧的参数更大，若A小于0，则昏侧的参数更大.

结果表明，磁层顶的运动速度和厚度在近日侧不对称度较小，之后逐渐加大，大概在90°～105°扇区内达到最大，随后至尾部又逐渐减小，中位数和平均值给出的结果大致一致.

与上文同样的原因，对于上游β值的不对称性仅用其中位数进行计算.结果显示，在105°扇区之前，晨昏两侧上游β的不对称并不明显，即不对称主要集中在近尾区域.在105°～120°扇区处不对称程度突然剧增，而后降低.与磁层顶运动速度和厚度的不对称程度分布相对比，不对称的分布区域并不相匹配，说明磁层顶上游β值的不对称可能并不是造成磁层顶厚度和运动速度不对称的主要原因.

2.4 旋转不连续和切向不连以及上游β对侧翼瓦伦关系的影响

本文采用特征参数|Q|对磁层顶两侧参数的瓦伦关系进行表征.|Q|区间为[0,1]，其值越接近1，表明瓦伦关系越好，穿越前后速度变化越接近阿尔芬度速度的变化，并依此划分了旋转不连续和切向不连续，结果如图13所示.

如图13,横轴为各事件计算得到的Q值的绝对值，纵坐标为所占比例，灰色条带为晨侧结果，黑色条带为昏侧结果.结果表明，|Q|在晨昏两侧均主要集中在0～0.1区间，这说明侧翼区域的磁层顶多为切向不连续.于此同时，相对昏侧，晨侧的|Q|值更接近1.

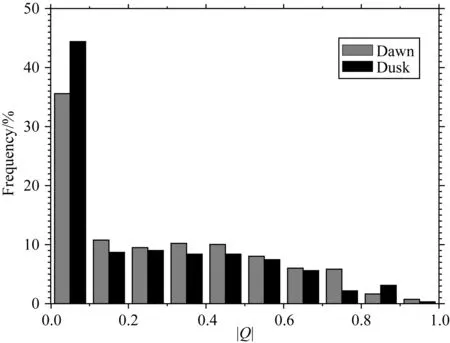
图13 瓦伦关系指示参数|Q|值的分布情况Fig.13 Statistical result of |Q|

本文以0.5为阈值划分切向不连续和旋转不连续，统计发现，磁层顶晨昏两侧旋转不连续事件个数占其对应区域事件总数的比例均在20%左右，晨侧略高，为22.3%(548个事件中有122个)，昏侧为18.6%(322个事件中有60个).

β对磁层顶重联活动的影响已经在之前的研究中被频繁提出，同时有研究表明在日侧区域，磁层上游的高β值对Walén关系有破坏作用.本文下面针对侧翼磁层顶区域上游β值对瓦伦关系的影响进行统计分析.

如图14，本文对晨昏两侧磁层顶分别进行了讨论，横坐标为上游β值，纵坐标为|Q|值，|Q|的阈值0.5已被横虚线画出.从图中可以看出，无论晨昏，当β值高于10时，几乎没有旋转不连续的情况发生.这表明，在低纬磁层顶的侧翼，磁层顶的上游高β值对瓦伦关系依然有破坏作用.

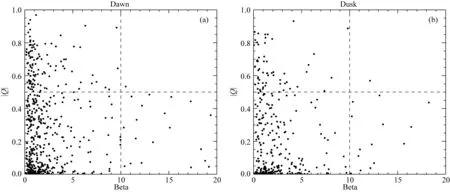
图14 上游β值对瓦伦关系的影响 (a) 晨侧结果; (b) 昏侧结果.Fig.14 The effect of upstream β value on Walén relation (a) The result of the dawn side magnetopause; (b) The result of the dusk side magnetopause.

3 总结和讨论

本文使用Cluster C3卫星的数据，主要应用MFR法对低纬侧翼磁层顶的运动速度、厚度等大尺度特征进行了计算，同时统计了对应区域磁层顶上游的β值，并分析了β对磁层顶大尺度参数的影响，讨论了上游β晨昏不对称影响磁层顶大尺度特征晨昏不对称的可能性，同时应用指示参数|Q|对磁层顶的TD和RD进行划分，分析了上游β值对瓦伦关系的影响，主要结果如下：

(1)低纬磁层顶侧翼的特征参数，如磁层顶厚度、速度、电流密度表现出明显的晨昏不对称性，即晨侧磁层顶更厚，电流密度更小，运动也更活跃.其不对称程度由近日侧到尾侧呈现先高后低的趋势.研究区域内的磁层顶厚度、速度绝对值由近日侧到尾侧均呈现递增趋势；

(2)低纬磁层顶侧翼上游β值主要集中在[0,2]区间，由近日侧到尾侧在整体上呈现递减趋势，有趣的是在昏侧距正午105°～120°扇区内，该值出现剧增.同时β值也呈现晨昏不对称，但是其不对称多集中于近磁尾区域，在105°扇区之前，晨昏两侧上游β的不对称并不明显；

(3)在低纬侧翼磁层顶区域，高上游β值对应更薄、更活跃的磁层顶，其区域的上游高β值对该区域的瓦伦关系有破坏作用；

(4)低纬磁层顶晨昏两侧区域的RD事件占比大致相当，均在20%左右.

对于磁层顶大尺度参数晨昏不对称形成的原因，尚未有定论.目前对可能造成这种不对称现象的几种猜测是：(1)近晨昏两侧磁层顶磁鞘区域内的动压和磁场场强存在差异；(2)晨昏两侧磁层顶受磁层内部物理过程影响；(3)晨昏两侧磁层顶附近的等离子体相对磁场速度不同.另外，考虑到太阳自转造成的行星际磁场的悬臂结构，本身可能也存在统计上的晨昏不对称现象，我们统计了磁层顶外侧激波为准平行和准垂直这两种情况的频率，以及两种情况下的磁层顶的特征参数.结果表明，两种情况在晨昏两侧出现的频率相差不是很大，同时两种情况下的晨昏不对称性均比较明显，且无太大差距，一定程度上表明上游磁鞘区域的激波方向可能不是造成晨昏不对称的主要原因.因此，我们认为观测到的磁层顶大尺度参数的晨昏不对称可能并不是由单一的上游等离子体参数造成的，很可能是多参数共同作用的结果.在今后的研究中，可以考虑联合其他的相关参数进行进一步的分析和研究，也可以考虑应用模拟的方法排除其他变量可能造成的影响，进而相对明确地判别可能造成这种磁层顶大尺度晨昏不对称的原因.

对于观测到的昏侧105°～120°扇区的上游β值异常抬升，有可能是由于C3卫星数据本身受某些因素或事件的影响造成了偏差，需要应用其他卫星进行进一步的验证.或者，也有可能是在该扇区存在特殊结构，这有待进一步研究.

致谢我们感谢欧洲航天局Cluster科学档案提供的Cluster卫星相关数据(https:∥csa.esac.esa.int/csa-web/#search).Karlheinz Trattner, Steven Petrinec和Stephen Fuselie提供并被收录于欧洲航天局Cluster科学档案的磁层顶穿越列表(https:∥www.cosmos.esa.int/web/csa/bow-shock-magnetopause-crossings-2001—2013).