含水砂岩蠕变损伤模型的二次开发及工程应用

赵立财

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300354； 2.台湾科技大学 营建工程系，台北 10607； 3.中铁十九局集团第三工程有限公司，沈阳 110136)

1 研究背景

岩石蠕变是指外界应力恒定的情况下，应变随时间增长而缓慢累积的现象[1]。岩石蠕变特性是岩石力学中的核心内容之一，由于其与岩体工程的长期稳定性紧密关系，受到国内外众多学者的广泛关注[2]。本构模型最主要描述岩石材料蠕变特性的方式，同时也是将蠕变试验研究成果用于工程实践的必经环节[3]。

现对于岩石蠕变的研究已有较多成果，Nedjar等[4]将损伤与Kelvin-Voigt模型耦合，建立了描述石膏岩石材料长期蠕变的损伤模型；王其虎等[5]提出裂隙岩石塑性变形体元件，建立了考虑初始损伤和蠕变损伤的蠕变本构模型；Jia等[6]以黏土岩为研究对象，引入损伤、渗透率演化和自愈建立渗流耦合蠕变本构模型，并通过ABAQUS进行二次开发；胡光辉等[7]引入岩石细观单元时效损伤的应力腐蚀模型，建立了基于离散元方法的岩石时效变形损伤破裂模型，进行数值模拟与室内试验的对比，证明所建立时效变形损伤破裂模型的合理性；胡浩[8]基于分数阶微积分理论建立蠕变本构模型，通过FLAC3D进行二次开发,并用隧道注浆加固的算例验证二次开发的有效性。

目前关于蠕变本构模型的研究已经达到硕果累累的地步，但对于二次开发及工程应用的系统研究较少。鉴于此，以某砂岩隧道为研究对象，开展砂岩饱和状态下的三轴压缩蠕变试验，建立考虑含水率的蠕变损伤模型，并将其推广为三维情形。将本构模型三维差分化，通过C++和FISH语言在FLAC3D中实现了二次开发。还原实际试验条件，进行仿真验证，证明二次开发成功及模型参数求取的正确性。建立隧道三维模型，调用自定义蠕变本构模型，进行不同蠕变时间下的数值计算，验证本文蠕变损伤模型在岩体工程应用中的可行性。

2 砂岩蠕变试验

蠕变试验采用RLW-2000型三轴流变试验系统，取样地点为某国家重点铁路项目隧道，该隧道长期处于富水环境，砂岩在水作用下蠕变变形显著，取砂岩制备成Φ50 mm×100 mm的圆柱样。首先进行常规三轴压缩试验，根据p=ρghk(p为压强，ρ为密度，g为重力加速度，h为深度，k为侧压力系数)，将k取为0.5(据经验)[9]，将围压σ3设置为4 MPa。假定岩石长期强度是三轴抗压强度的75%～80%[10]，据此进行蠕变试验各级偏应力水平的设置，将偏应力水平设为5级，分别为三轴抗压强度的40%、50%、60%、70%和80%。经玻尔兹曼线性叠加处理[1]，围压4 MPa下饱和状态的分别加载蠕变曲线如图1所示。通过等时偏应力-应变曲线取拐点的方法确定长期强度[11]，如图2所示。

图1 分别加载蠕变曲线Fig.1 Creep curves under separate loading

图2 等时偏应力-应变曲线Fig.2 Isochronous deviatoric stress-strain curves

由图1可看出，砂岩在加载瞬间产生瞬时变形，接着出现衰减蠕变阶段，该阶段历时不超过10 h，应变率逐渐降低，随即岩石进入应变率基本恒定的稳定蠕变阶段，当达到破坏偏应力水平时，还表现有加速蠕变阶段。

由图2可知，岩样在1 h时间节点时，偏应力-应变关系为线性，11 h以后的偏应力-应变关系均表现出明显的非线性特征，曲线逐渐偏于应变轴。

3 考虑含水率的蠕变损伤模型

3.1 考虑含水率的损伤变量

蠕变损伤变量中考虑含水率的影响，对于研究不同含水状态下的岩石蠕变及损伤特性具有重要的意义。根据损伤力学理论中能量损伤按弹性模量变化[12]定义的方法，将含水率引入其中，认为工程岩体在初始状态下的弹性模量为E0，受扰动或水岩作用影响下，岩石材料的弹性模量逐渐衰减直至一个稳定值，由此提出一种考虑含水率的负指数蠕变损伤表达式，即

D(t,ω)=1-e-δωt。

(1)

式中：D为损伤变量；ω为含水率；t为时间；δ为与损伤程度有关的参数。

根据上式定义3种状态：①当t=0或ω=0时，损伤变量D=0，此时材料无损；②ω的增加会增强损伤累积，但是岩石的ω一般情况下不会超过15%，不会存在趋于无穷大的情况；③当t→∞时，损伤变量D=1，此时材料完全损伤。当时间t逐渐增长时，损伤变量D逐渐趋于1。

假设岩石材料为各向同性损伤，则有

PD=P0[1-D(t,ω)] 。

(2)

式中：PD为考虑损伤的流变参数;P0为无损状态的流变参数。

3.2 考虑含水率的蠕变损伤模型构建

在构建蠕变损伤模型之前，首先进行砂岩流变性态分析。本文砂岩在加载瞬间首先产生瞬时弹性变形，岩石表现为瞬时力学形态，可以用H体来描述。由图2可知，岩石的等时应力-应变关系非线性特征显著，这表征出岩石具有一定的黏弹性，可用开尔文体(H|N结构)进行描述。瞬时变形之后，岩石进入衰减蠕变阶段，相比瞬时弹性变形，其蠕变速率急剧下降，当应力水平小于长期强度时，蠕应变在稳定蠕变阶段会趋于一个恒定值，说明岩石还具有一定黏性，可用N体进行描述。而当应力水平超过长期强度，岩石进入加速蠕变阶段，应变快速增长，经过较短时间最后破坏，这体现出岩石的黏塑性，所以模型中应有宾汉体。综上所述，认为本文砂岩的流变性态为黏性-黏弹性-黏塑性，通过统一流变力学模型理论[13]确定其模型结构为H-N-H|N-N|S，如图3所示。

图3 H- N -H|N -N|S模型示意图Fig.3 Schematic of H- N-H|N-N|S model

当σ0<σS(σS为长期强度)时，黏塑性体失效，模型退化为H-N -H|N结构，变为传统的Burgers模型，相应的状态方程为

(3)

相应的蠕变方程为

(4)

式中：σ0为初始应力；σ1、ε1、E1、η1分别为Maxwell体的应力、应变、瞬时弹性模量和黏滞系数；σ2、ε2、E2、η2分别为Kelvin体的应力、应变、弹性模量和黏滞系数；σ3、ε3、η3分别为宾汉体的应力、应变和黏滞系数;上标圆点为变量对时间t的一阶导数,下同。

当σ0≥σS时，黏塑性体发挥作用，模型相当于西原模型中黏塑性体与传统的Burgers模型的结合，相应的状态方程为

(5)

相应的蠕变方程为

(6)

式(4)和式(6)为H- N -H|N -N|S结构模型的蠕变本构方程，本文认为当应力水平超过长期强度时，此时损伤迅速累积[12,14-15]，所以对塑性元件进行损伤演化。根据Lemaitre等效应力原理[16]，对式(4)和式(6)进行损伤演化可得

(7)

式(7)即为本文所建考虑含水损伤的一维蠕变本构模型。

3.3 蠕变损伤模型三维拓展

岩石多处于二维、三维的应力状态，难以描述岩石在多向应力状态下的蠕变行为，因此需将式(7)拓展为三维情形。假设岩石为各向同性体，根据广义Hooke定律，三维应力状态下的本构关系为

(8)

式中：σm为球应力张量；Sij为偏应力张量；K为体积模量;εm和eij分别为球应力和偏应力张量所对应的应变;G为剪切模量。分解岩石内部的应力张量，于是有

σij=Sij+δijσm。

(9)

式中：σij为应力张量；δij为单位张量。

一般认为，在三维应力下，岩石体积蠕变近乎为0，本文三维蠕变方程中不考虑体积蠕变，仅考虑瞬时体积变形，并引入屈服函数F来描述岩石的屈服。由此将式(7)推广为三维应力状态，即

(10)

式中：(Sij)0为初始偏应力张量；(Sij)S为长期强度对应的偏应力张量；F0为屈服函数的初始值；Q为塑性势函数。

屈服函数可以取如下形式：

(11)

式中J2为应力偏量第二不变量。

在等围压三轴压缩应力状态下，中间主应力与围压量值相等，于是有

(12)

令屈服函数初始值F0=1，相关联的流动法则Q=F[17]，将式(12)代入式(10)可得

ε11(t)=

(13)

式(13)即为本文所建立考虑含水率的三维蠕变损伤模型的轴向蠕变方程。

3.4 模型参数确定

本文所建考虑含水率的三维蠕变损伤模型有G1、G2、K、η1、η2、η3、δ、ω和(σ1-σ3)S共9个参数。其中(σ1-σ3)S为岩石长期强度，通过等时应力-应变曲线法已确定为19.84 MPa，岩石试验确定含水率ω为3.47%。另外7个参数则利用数学优化软件1stOpt，选取BFGS(Quasi-Newton)算法，通过式(13)辨识图1中的分别加载蠕变曲线，得到模型参数如表1所列。

表1 模型参数Table 1 Model parameters

4 蠕变损伤本构模型二次开发

4.1 模型三维差分化

参照文献[18]中内置Cvisc模型部分内容以及该模型的C++程序源代码推导了蠕变损伤模型(示意图如图4所示)在三维条件下的中心差分形式。

图4 蠕变损伤模型示意图Fig.4 Schematic diagram of creep damage model

该模型将Maxwell模型、Kelvin模型和一个考虑含水损伤的黏塑形体串联，包括了弹塑性体积应力应变行为和黏弹塑性偏应力应变行为，其中偏应力应变行为可由以下公式反映，即

(14)

Maxwell体、Kelvin体及黏塑性体(黏塑性体以服从Mohr-Coulomb(简称M-C)准则的塑形元件表示)的偏应力-应变本构关系方程分别为：

(15)

(16)

(17)

体积应力-应变关系为

(18)

式中：evol和Svol分别为体积应变张量和体积应力张量，带圆点的变量表示对时间的一阶微分；g为M-C单元的塑性势函数；λ为待定系数；K和G分别为岩石的体积模量和剪切模量；η为黏滞系数。

M-C单元的破坏包络线服从M-C准则，屈服准则f=0，其表达式为:

(19)

(20)

式中：σ1、σ3分别为最大主应力和最小主应力；c、φ、ψ分别为黏聚力、内摩擦角和剪胀角。

以增量形式表示式(14)为

(21)

对式(15)中心差分可得

(22)

式(15)和式(18)可写为

(23)

(24)

(25)

(26)

式中上标N和O分别表示一个时间增量步内新、老量值。

将式(25)和式(26)代入式(22)可得：

(27)

(28)

将式(23)、式(27)代入式(21)，再结合式(25)、式(26)可得：

(30)

(31)

式(24)可以写为

(33)

其中：

(34)

(35)

以上就是蠕变损伤模型的三维差分形式。

4.2 编程概要

基于推导得到的蠕变损伤模型三维差分形式，利用 FLAC3D软件提供的本构模型二次开发程序接口，采用C++语言在Visual Studio 2008平台上对Cvisc模型源代码进行修改。私有变量须事先定义好dω1，dδ1(ω为含水率，δ为与损伤累积有关的参数)等及6维数组中间变量dMekd[18]。程序文件中还须对模型结构、Property函数、State函数、Initialize函数、Run函数等程序文件进行修改。程序文件编写完成后，将自定义本构模型代码编译成动态链接库文件，在 FLAC3D软件中调用该文件即可应用自定义本构模型。

4.3 仿真验证

为了验证蠕变损伤本构模型的合理性和正确性，基于FLAC3D进行仿真模拟，数值模型以实际岩样规则为准，建立直径50 mm，高100 mm(设为Z方向)的圆柱形试样模型(如图5所示)，共划分为876个节点，660个单元。计算模型底部施加Z方向的约束作用，顶部施加均布荷载，这里的均布荷载是指轴向应力(轴向应力为偏应力与围压之和)。侧面施加与三轴压缩蠕变试验相同的均布径向荷载，围压设为4 MPa，应力条件与实际三轴压缩蠕变试验保持一致。

图5 仿真模型示意图Fig.5 Simulation model

为验证蠕变损伤模型在FLAC3D程序中的模拟结果的正确性，根据不同应力水平三轴蠕变模拟试验，将表1中的模型参数写入FISH命令，通过仿真计算得到试件顶部中心的竖向位移量，换算成轴向应变量，与试验曲线进行比较，得到模拟效果如图6所示。

图6 模拟效果Fig.6 Simulation results

由图6可看出，模拟结果与试验曲线较为吻合，拟合效果较好，通过这样的方法反演验证了蠕变模型参数的正确性，同时证明蠕变损伤模型在FLAC3D程序中二次开发成功。

5 工程应用

研究区隧道为国家铁路重点工程项目，围岩具有较强流变特征，现隧道已通车运营近2 a，将本文考虑含水率的蠕变损伤模型应用于该隧道，以验证模型有效性。

5.1 工程概况

研究区隧道进口里程DIK4+868，出口里程DIK6+000，隧道全长1 132 m，隧道最大埋深52.91 m。

隧道DIK5+250—DIK5+450段200 m范围内依次下穿环城公路及人行天桥基础，其中DIK5+337下穿环城公路，与公路垂直相交，隧道埋深18～22 m。隧道穿越J3jf砂岩地层，砂岩地层上覆砾岩。由于雨水与超重货车通行影响，砾岩渗透率高，进而导致下层砂岩遇水软化现象发生，导致隧道围岩变形增大。隧道支护截面如图7所示。

图7 隧道支护截面Fig.7 Section of tunnel support

由图7可看出，隧道支护手段为“锚固组合式预应力锚杆+初衬+二衬+可压缩层”，其中隧道支护所用锚杆有别于传统锚杆，该锚杆为锚固组合式预应力锚杆，锚杆尾端和可压缩泡沫混凝土连接在一起，形成的压缩区将形成岩体的承载拱(环)。由于拱效应作用，在锚杆上施加相对较低的预应力后，围岩的自承能力就能得到了充分调动，对拱外侧围岩的抗力得到极大提升。

5.2 模型建立

为减小边界条件的影响，模型左右边界到隧道中心的距离取为隧道5倍洞径，隧道下部边界取为隧道2倍洞径进行建模，隧道内半径7.98 m，外半径8.93 m和9.18 m，整体尺寸取为90 m(宽)× 70 m(高)，隧道中心到公路路面距离为18 m，公路两侧边坡高度为9.76～7.38 m，隧道底部以下为20 m，左右边界分别离隧道中线45 m，纵向延伸50 m，隧道位于模型的正中心。隧道模型(图8)共划分97 868个六面体实体单元，106 106个节点。

图8 隧道模型Fig.8 Tunnel model

可压缩泡沫混凝土、初期支护、二次衬砌材料均采用Mohr-Coulomb本构模型、可压缩泡沫混凝土采用crush-form本构模型，砾岩、砂岩层均采用自定义蠕变损伤本构模型，已开挖部位为null model空模型。路面定义为壳单元(shell)，隧道初期支护、二次衬砌定义为衬砌单元(liner)，预应力锚杆定义为单元锚索单元(cable)，建模时砂岩层、砾岩层、初期支护、二次衬砌、可压缩泡沫混凝土均定义为六面体实体单元。砂岩、砾岩饱和状态瞬时物理力学参数及蠕变模型参数分别如表2和表3所示。初期支护参数、二次衬砌及可压缩层参数如表4所列，锚杆加固区力学参数如表5所列，环城公路路面参数如表6所列。

表2 砂岩、砾岩饱和状态瞬时物理力学参数Table 2 Transient physical and mechanical parameters of saturated-state sandstone and gravel

表3 砂岩、砾岩饱和状态蠕变模型参数Table 3 Creep model parameters of saturated-state sandstone and gravel

表4 隧道初期支护、二次衬砌和可压缩层力学参数Table 4 Mechanical parameters of primary support, secondary lining and compressible layer of tunnel

表5 锚杆加固区力学参数Table 5 Mechanical parameters of anchor reinforcement

表6 路面相关参数Table 6 Related parameters of pavement

5.3 数值计算结果

模型蠕变时间设定为1 a、5 a和20 a，在拱顶、拱腰等部位设监测点。蠕变时间1 a的位移场云图如图9所示。现场位移监测设置照片如图10所示。

图9 蠕变1 a的位移场云图Fig.9 Displacement field with one year of creep

图10 现场位移监测设置Fig.10 Setup of field displacement monitoring

由图9可看出，拱顶部位的位移最大，拱底位移最小，拱顶部位是隧道的危险位置。将蠕变1 a的模型拱顶监测与隧道实际营运1 a的拱顶监测位移进行对比，如图11所示。

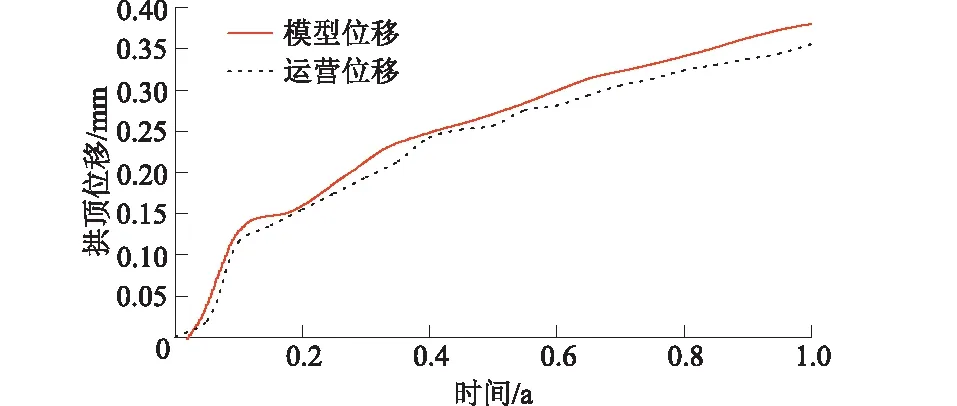
图11 蠕变1 a的拱顶位移监测对比Fig.11 Comparison of monitored displacement of vault with one year of creep

由图11可看出，模型拱顶监测位移与实际运营监测位移较为吻合，前者略高于后者，可为隧道围岩变形控制提供一定的安全预留空间。蠕变时间1 a的数值模拟较为成功，由此证明本文隧道数值模拟方法及蠕变损伤本构模型的可行性，接下来数值分析蠕变时间5 a和20 a的情况，可为隧道后期安全营运提供参考。蠕变5 a和20 a的位移场云图如图12所示。

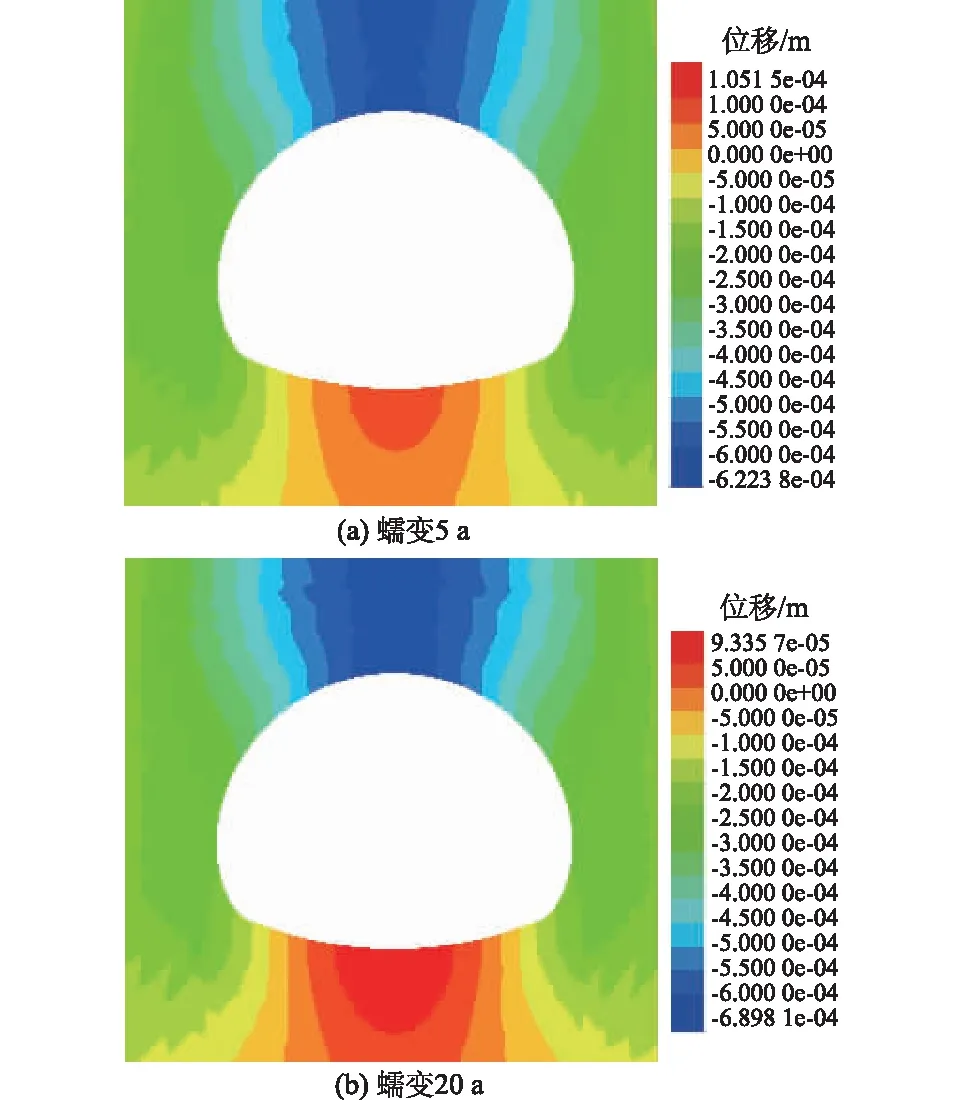
图12 蠕变5 a和10 a的位移场云图Fig.12 Displacement fields with five years and ten years of creep

由图12可看出，蠕变时间5 a和20 a时，拱顶位移始终最大，拱底位移始终最小。由此说明该隧道拱顶位置的安全监测需重点关注。蠕变20 a时数值模型拱顶预测位移如图13所示。

图13 蠕变20 a拱顶位移预测结果Fig.13 Predicted displacement of vault with 20 years of creep

由图13可看出，蠕变20 a时模型拱顶预测位移达到0.668 mm，蠕变时间从0到5 a，位移以较快速率累积，从5 a到20 a时，拱顶位移呈现缓慢增长的趋势。当蠕变时间达到20 a时，拱顶位移趋于收敛，由此可认为“锚固组合式预应力锚杆+初衬+二衬+可压缩层”的支护手段能满足隧道长期运营安全需求。

6 结 论

(1)砂岩流变性态为黏性-黏弹性-黏塑性，通过统一流变力学模型理论确定砂岩蠕变模型结构为H- N -H|N -N|S，以此为基础模型从而进行改进。

(2)建立考虑含水率的负指数蠕变损伤表达式，应用于H- N -H|N -N|S结构元件模型，并推广到三维应力状态，从而得到新的蠕变损伤本构模型。

(3)将蠕变损伤模型三维差分化，通过C++和FISH语言在FLAC3D中实现了二次开发。还原实际试验条件，进行仿真验证，模拟值与试验值较为吻合，证明了二次开发成功及模型参数求取的正确性。

(4)以实际隧道工程为研究对象，建立三维模型，调用自定义蠕变本构模型，进行蠕变1 a、5 a和20 a的数值计算。蠕变1 a时，模型拱顶监测位移与实际运营监测位移较为吻合，由此证明本文隧道数值模拟方法及蠕变损伤本构模型的可行性。

(5)蠕变20 a时模型拱顶监测位移达到0.668 mm，此时位移趋于收敛。证明本文采取“锚固组合式预应力锚杆+初衬+二衬+可压缩层”的支护措施的有效性，且该支护措施能满足隧道长期运营安全需求。

本文自行构建了岩石蠕变损伤本构模型，在FLAC3D中进行二次开发，调用自定义本构进行砂岩隧道数值分析，证明了本文模型在砂岩隧道蠕变分析中的可行性。由于本文模型基于砂岩蠕变数据而构建，该模型能否用于描述其他种类岩石的蠕变行为待验证，故该模型在其他地层岩性隧道中的适用性待进一步考证。本文隧道围岩处于富水环境，后续研究中隧道数值分析还应考虑流-固耦合作用的情况。