分流量区间BMA方法在小流域暴雨山洪模拟中的应用——以官山小流域为例

刘杨合，程 磊，张云帆，张艳军，卫晓婧

(1.武汉大学 水资源与水电工程科学国家重点实验室， 武汉 430072； 2.武汉大学 水利水电学院， 武汉 430072)

1 研究背景

山洪是突发性降雨导致的山区径流陡涨陡落的自然现象，受降雨强度和下垫面等因素影响，可能伴有泥石流和滑坡等灾害的发生，严重威胁着国民经济增长和人民生命财产安全[1]。小流域山区洪水具有突发性、局地性和频次多等特点[2]，不同流域山洪致灾机理差异性较大，受地形条件和资料缺乏所限，以及人为因素影响，小流域山区洪水一直存在着模拟精度低、预报精度差的问题[3-4]。因此，开展小流域山区洪水模拟的相关研究对保障社会经济增长、维护人民生命财产安全等具有至关重要的作用。

秦巴地区是我国重要的山洪灾害防治区，1950—2000年防治区内共有小流域2 411个，山洪沟1 765条，山洪灾害次数共8 251次，其山洪灾害严重程度仅次于江南丘陵和华南丘陵地区[3-4]。本研究选取的官山小流域，以中小丘陵为主，多暴雨和长历时降雨，具有典型的秦巴地区气候和地形特征。官山小流域内山洪频发，自1975年以来，发生了12场危害性较大的山洪灾害。其中1975年山洪冲毁河堤24.2 km，受淹农田面积2 426 hm2；2012年8月5日山洪冲毁公路160 km，毁坏桥梁29座，转移人口约7 000人，直接经济损失达2.3亿元。

作为秦巴地区的典型流域，官山小流域洪水模拟相关研究已初步开展，韩培等[5]利用GIS技术获取了官山小流域的地形、坡度、植被覆盖度、土地利用类型等下垫面特征，为洪水模拟提供了基础数据支撑。王以逵等[6]研究了官山河两河口河段的暴雨洪水顶托效应。黄艳等[7]比较分析了改进的SCS(Soil Conservation Service)、TOPMODEL和新安江模型在官山河流域洪水模拟中的应用效果。然而当前官山小流域洪水模拟仍然存在以下2个问题：①传统水文模型洪水模拟精度较低；②各模型模拟不同场次洪水的能力差异大，水文模型挑选难。

本研究利用官山小流域2009—2015年10场降雨径流关系较好的场次洪水，分别采用新安江、TUWMODEL和TOPMODEL等模型进行模拟。基于各模型模拟结果，采用分流量区间BMA(Bayesian Model Averaging)方法[8]综合计算官山小流域场次洪水过程，并与3种单一模型模拟精度进行比较分析，以期提高官山小流域山洪模拟精度，为提高秦巴地区洪水预报精度提供技术支撑。

2 研究区概况

官山小流域坐落于汉江中上游、丹江口市西南部，位于110°48′00″E—111°34′59″E，32°13′16″N—32°58′20″N，出口孤山水文站控制的流域面积为332 km2，流域人口密度达241人/km2。以山地丘陵为主，海拔240～1 606 m，平均高程690 m，河道平均坡降5.7%，多年平均流量7.78 m3/s。流域降雨以局地性暴雨和连阴雨为主，年降水量为1 100 mm。山洪及其造成的泥石流和滑坡灾害频发。研究区降雨由孤山站、袁家河站、大马站和西河站的降雨观测数据通过泰森多边形法计算得到，流量数据选用孤山站的水文监测数据。研究区的地理位置、雨量站和水文站的分布如图1所示。

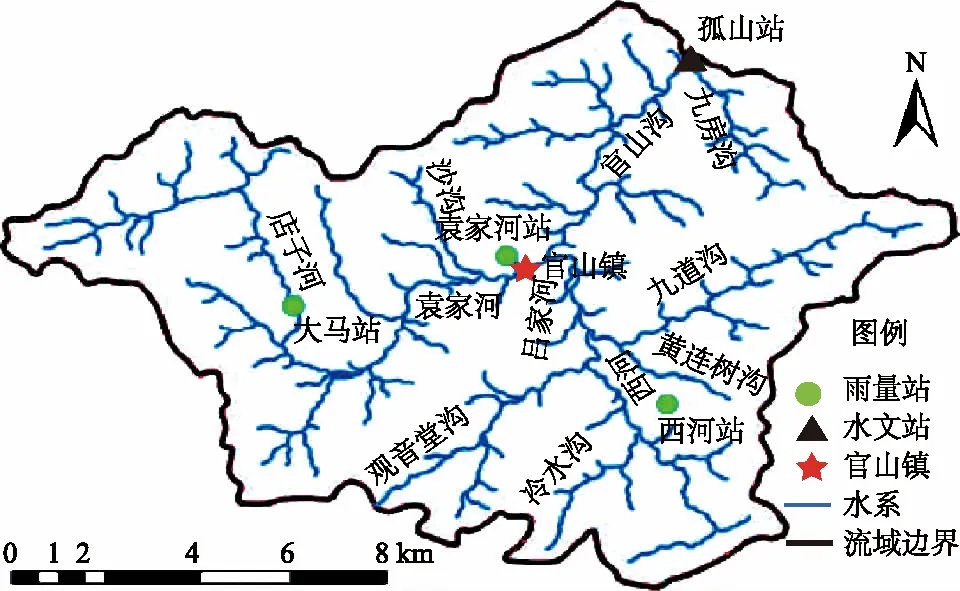
图1 官山小流域地理位置Fig.1 Location of Guanshan small watershed

3 研究方法

3.1 TOPMODEL模型

TOPMODEL模型是一个基于地形的半分布式水文模型，由Beven和Kirkby于1979年提出[9]。模型自提出以来，已在水文领域得到了广泛应用，其核心在于利用地形指数ln(α/tanβ)来反映以径流运动分布规律为主的流域水文现象[10]。其中,α为流域面积，β为流域坡度。

TOPMODEL模型主要采用饱和产流机制，即地下水达到地表时，土壤含水量达到或超过饱和含水量，流域产生饱和坡面流。模型具有3层结构，分别为植被根系层(Srz)、土壤非饱和层(Suz)和饱和地下水层(D)；将目标流域划分为多个单元网格，降水首先按一定速率下渗进入植被根系层补给该部分的土壤缺水量，植被根系层的水分损失为蒸发和下渗，当降水满足该层的土层储水能力和蒸发损失后，剩余部分水分下渗进入土壤非饱和层。土壤非饱和层中的水分按一定重力排水速率VG下渗进入饱和地下水层，并最终经由侧向径流形成壤中流Qb。饱和地下水层受到土壤非饱和层的补给后，随着地下水位的上升，流域下游河道会产生饱和坡面流Qs。流域总径流Q等于壤中流和坡面流的总和，即Q=Qb+Qs。

3.2 新安江模型

新安江模型是集总式水文模型，由赵人俊于1984年提出[11]。该模型结构简单，模型参数概念明确，且已在我国南方湿润流域的水文模拟研究得到广泛应用。模型核心为蓄水容量曲线，首先计算各蓄满单元流域的产汇流，得到各单元流域的出口流量过程后，进行出口以下的河道洪水演算，叠加各单元流域的出流过程，进而获得流域总径流过程。模型的蒸散发结构为3层；产流计算过程采用严格的蓄满产流模式，以田间持水量为控制条件，流域单元土壤含水量达到田间持水量，流域单元内净雨全部转化为径流；总径流为地表径流、壤中流和地下径流三者之和；地表径流汇流计算采用单位线法；壤中流和地下径流的汇流计算采用线性水库法。

3.3 TUWMODEL模型

TUWMODEL模型是维也纳工业大学开发的集总式水文模型。模型的核心是产流随土壤湿度呈指数变化。该模型包含融雪模块、土壤水模块和径流模块。融雪模块通过简单的度日因子法计算融雪过程；土壤水模块表示产流和流域土壤水的变化。产流机制与新安江模型不同，模型采用接近蓄满产流的概念，产流量主要受土壤湿度控制，是土壤湿度的指数函数，与降雨强度无关，土壤越湿，越容易产流；径流模块包含上下层水库，土壤水模块的水量可以下渗到上层水库，上层水库的水分会产生地表径流和壤中流并可以通过下渗进入下层水库，下层水库以一个较小的速率产生径流。上下层水库产生的径流三角函数进行汇流计算。

3.4 分流量区间BMA方法

3.4.1 BMA方法

BMA方法是通过加权平均多个模型的模拟结果以期获得更为可靠的综合模拟结果[12]。基于BMA方法原理，可以根据k个模型(f1,f2,f3,…,fk)的独立分布，计算综合各模型模拟流量Q的总概率分布P(Q|OBD)，进而计算综合各模型模拟结果的模拟流量Q。其计算过程如下。

总概率分布为

式中：OBD为观测流量样本数据；fi为所选模型；pi(Q|fi,OBD)为所选模型的后验分布。

综合模拟流量Q通过计算总概率分布的均值获得，即

式中：g(Q|fi,σ2)为模型fi同观测流量做线性回归获得的分布；σ为所得分布的标准差。令p(fi|OBD)=ωi，则可得

(3)

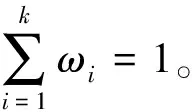
3.4.2 流量区间划分

各模型结构和产汇流机制不同，导致了不同模型在模拟不同量级的洪水流量过程时，往往具有不同的表现能力和相对优势。相较于传统的BMA方法，分流量区间BMA方法考虑不同模型模拟不同量级洪水过程时相对优势的差异，为模型分配一个随洪水流量量级发生变化的模型权重，可以更好地发挥不同模型模拟不同量级洪水过程的优势，提高洪水模拟精度[8]。本研究首先将率定期内所有场次的雨洪过程拼接成长序列的雨洪过程，以该长序列的降雨流量数据分别率定新安江、TUWMODEL和TOPMODEL水文模型。按分位数(10%、25%、50%、75%、90%、100%)将长序列流量过程划分为6个子区间，分别提取出3个单一模型在对应子区间模拟的流量过程。在6个子区间内，以划分出的实际流量过程为BMA方法中的观测样本数据(OBD，见3.4.1节)，以模型模拟的流量过程为模型后验分布(pi(Q|fi,OBD)，见3.4.1节)，基于BMA方法分别计算各子区间内新安江、TUWMODEL和TOPMODEL各水文模型的模型权重。检验期洪水计算则根据洪水流量所处区间，采用分区间BMA方法计算的模型权重和检验期模型模拟的流量过程，加权平均各模型优势的模拟流量过程。

3.5 模型参数率定与评价指标

模型误差评价指标如下：

(1)纳什效率系数NSE计算公式为

(4)

(2)水量平衡系数VE计算公式为

(5)

(3)洪峰流量相对误差Qe计算公式为

(6)

式中：Qe为洪峰流量相对误差；Qp,sim和Qp,obs分别为洪峰流量模拟值和观测值。本研究中流域洪峰流量平均相对误差为所有场次洪峰流量相对误差的均值，许可误差为实测值的±20%[15]。

(4)洪量相对误差Ve计算公式为

(7)

式中：Ve为洪量相对误差；Vsim和Vobs分别为洪量的模拟值和观测值。本研究中流域洪量平均相对误差为所有场次洪量相对误差的均值，许可误差为实测值的±20%[15]。

(5)峰现时间误差Te计算公式为

Te=Tsim-Tobs。

(8)

式中：Te为峰现时间误差；Tsim和Tobs分别为峰现时间的模拟值和观测值。本研究中流域平均峰现时间误差为所有场次峰现时间误差绝对值的均值，许可误差为3 h[15]。

(6)合格率QR计算公式为

(9)

式中：QR为合格率；N为合格的模拟次数；M为总的模拟次数。

针对以上各指标，纳什效率系数越接近于1,说明该模型模拟洪水流量的整体过程越好；VE越接近于0,说明该模型模拟洪水过程中水量平衡模拟得越好；洪峰流量、洪量相对误差和峰现时间相对误差越接近于0，说明该模型模拟的洪峰流量、洪量和峰现时间越准确；洪峰流量、洪量和峰现时间合格率越接近于100%，说明使用该模型模拟的洪峰流量、洪量和峰现时间的可靠性越高。

4 结果分析

图2对比分析了分流量区间BMA方法和3个水文模型的流量模拟结果在率定期和检验期的水量平衡系数和纳什效率系数之间的差异。结果表明：分流量区间BMA方法在检验期的纳什效率系数显著高于3个单一水文模型，率定期和检验期的中位数分别为0.87和0.79；水量平衡系数中位数分别为-8.8×10-11和0.02，比3个单一水文模型的水量平衡系数的中位数更接近0。

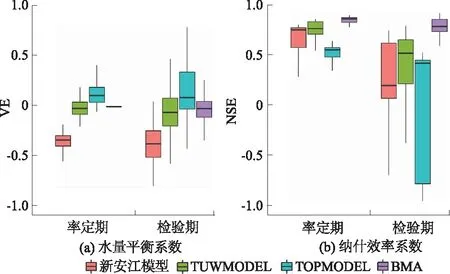
图2 率定期及检验期各模型评价指标对比Fig.2 Comparison of evaluation indices in calibration period and verification period among different models

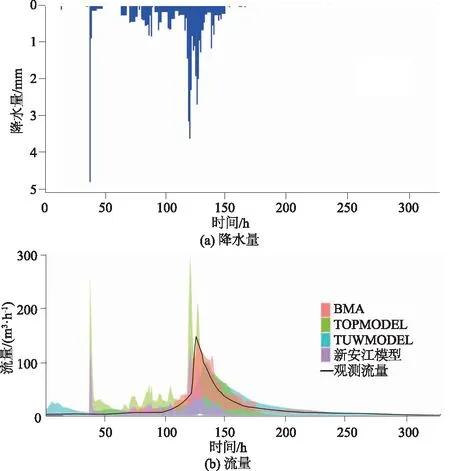
图3 20100825号洪水期间降雨径流过程 Fig.3 Rainfall and runoff processes during flood event 20100825

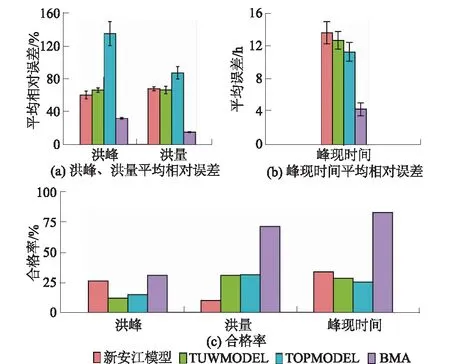
图4 检验期洪峰、洪量及峰现时间平均相对误差和合格率Fig.4 Averaged relative errors and pass rate of flood peak, flood volume, and time of peak in verification period

5 讨 论

分流量区间BMA方法可以计算出模型在各流量区间的模型权重，分析模型权重在不同区间的相对大小，可以为官山小流域挑选适用水文模型的提供参考。图5显示了分区间BMA方法估计的新安江模型、TUWMODEL和TOPMODEL在不同流量区间的模型权重。由图5可以看出，新安江模型仅在流量区间为90%～100%时具有较高的模型权重。TUWMODEL在各区间的模型权重的中位数(除90%～100%外)均大于新安江模型和TOPMODEL，且在50%～75%和75%～90%区间内高达0.85和0.82。TOPMODEL在各区间的模型权重中位数均较小，其模型权重中位数仅在25%～50%区间内略高于新安江模型。其原因可能在于不同区间洪水的产汇流机制不同，各模型仅在符合自身产汇流假设的条件下得到更好的模拟效果，从而被分配到较高的权重。新安江模型采用蓄满产流机制[16-17]，故仅在降雨量较高，流域发生大洪水时，官山小流域的土壤含水量趋近于饱和时具有更高的模型权重。TUWMODEL采用的产流机制不是严格的蓄满产流，其产流量是土壤含水量的指数函数，受降雨强度约束较小，主要受土壤湿度控制，土壤越湿流域越容易产流[16, 18-19]。该产流机制可能比较符合官山小流域的暴雨山洪产流特性。虽然TOPMODEL考虑了地形因素，但因其模型的表现受洪峰影响较大，而所选的10场洪水，洪水量级差异明显，故在模型率定过程中难以确定最优参数，致使模型表现性能较差[7, 20]。

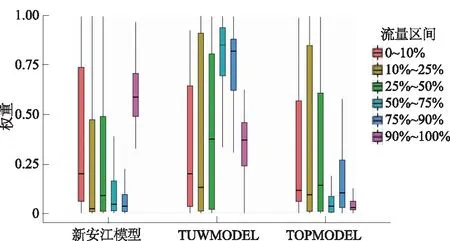
图5 新安江模型、TUWMODEL和TOPMODEL权重Fig.5 Weights of Xin’anjiang model, TUWMODEL, and TOPMODEL

6 结论与展望

针对小流域山区洪水模拟精度较低及缺乏水文资料带来的洪水模拟可靠性低的问题，本研究以秦巴地区内的典型小流域官山小流域为例，选取了2009—2015年10场降雨径流关系较好的场次洪水，将其中任意7场作为率定期，剩余3场作为检验期，分别率定了新安江模型、TUWMODEL和TOPMODEL。基于以上3种模型的模拟结果，利用分流量区间BMA方法估计了综合各模型优势的模拟洪水流量过程，并对比了该方法的模拟结果和其他3种单一模型的差异。结果显示，分流量区间BMA方法相比于其他3种单一水文模型更好地模拟了该区域的洪水过程。其检验期纳什效率系数的中位数为0.8，远高于其他3种单一水文模型。其检验期的洪峰流量、洪量和峰现时间合格率分别为30.6%、70.8%和82.2%，高于其他3种单一水文模型，较于最优水文模型分别高出4.5%、39.7%和48.9%。模型的权重结果显示，TUWMODEL相较于其他2种水文模型在官山小流域更为适用，其原因在于TUWMODEL的产流机制更符合官山小流域。

本研究仅选取了3个水文模型运行分流量区间BMA方法，未来的研究中可以增加水文模型的数量，选取更多的具有不同产汇流机制的水文模型运行分区间BMA方法；也可使用不同目标函数率定的水文模型运行分流量区间BMA方法，来全面分析不同目标函数对不同流量区间官山小流域流量过程的影响。此外，分流量区间BMA方法在产汇流机理相比于产汇流假设固定的单一水文模型，在复杂的山区小流域具有较好的适用性，对于雨洪资料匮乏、产汇流机制研究不完善的山区小流域，使用分流量区间BMA方法可以综合各模型模拟优势，提高山区小流域的洪水模拟精度。对于资料比较丰富、能够有效进行分析和推断产流机制和山洪形成过程的流域，应该更多从物理机制入手，建立合理的物理过程模型。