分析力学中变分原理阐述与应用

薛皓翔

（兰州大学核科学与技术学院，甘肃兰州 730000）

0.引言

分析力学是一门以广义坐标为描述质点系的变量，以虚位移原理和达朗贝尔原理为基础，运用数学分析问题的角度出发，从而研究宏观现象中的力学问题。分析力学的基本内容是阐述力学的普遍原理，由这些原理出发导出质点系的基本运动微分方程，并研究这些方程本身以及它们的积分方法。分析力学是经典物理学的基础之一，也是整个力学的基础之一。它广泛用于核结构分析，航天力学以及各种动力学分析的实际工程应用中。作为其核心的变分法，透彻研究其分析问题的机理也具有较高地实际意义。

1.变分原理

所谓变分法，通俗地讲，即研究泛函极值的一种手段或者说是方法，那么泛函又是函数的函数，更一般地说，在我们分析力学中所研究的泛函（I）指的是一个函数的集合（M）映到实数（R）的一个映射[1]。

那么为了更加清晰明了地阐述或者说表达我们所说的变分原理，我们假定有两个曲线

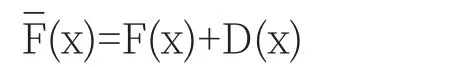
我们将D(x)中拿出一个系数ε，则可以写为D(x)=εξ(x)，而我们将D(x)称之为F(x)的变分，记为δF(x)，其中ε为一个常数，当然通常在用变分法研究泛函极值的时候，ε通常为一个无穷小量，ξ(x)是自变量为x的任意函数，另外一曲线ξ(x)那么我们可以把ξ(x)看作是引起变分的一种扰动，此时我们对泛函变分问题的认识可能会更加具体，

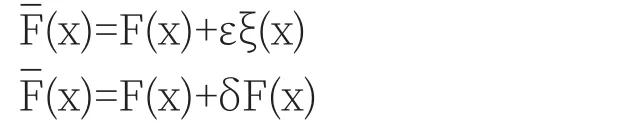
变成了一个只有一个常数ε的函数组，即我们之前所提到的函数的集合，为了更清晰的认识这个问题，我们以最速曲线为实例，可以更好的说明我们想要表达的问题。

考虑最速曲线的实例，那么-F(x)则为其他的各种可能性（这种可能性是任意的），这也就是我们之前所提到的函数组，此时ξ(x)需要满足两个条件[1]：

（1）ξ(x)在A、B两点处为零，即δF(x)在A、B处为零，否则我们所讨论的问题将会改变，以至于接下来的讨论将没有意义；

（2）ξ(x)连续，其1、2阶导数存在。

接下来我们来讨论一下上式，其中的ε我们可以将其认为成控制因子，只有在ε=0的，取得极值，而ε为无穷小量也正是变分法的精妙之处，而ξ(x)即为我们之前所提到的一种扰动，它决定着趋于零的方式。

2.最速曲线

不同的ε对应不同的曲线，相应的与泛函所对应的不同的实数值，其中的ε1、ε2、ε3所对应的时间T也不相同，只有当ε=0（或者说无穷趋向于0）时，函数组-F(x)趋向于最速曲线所对应的F(x)，而我们提到的ξ(x)则决定着趋向于零的不同方式，当然这种趋向方式也是任意的。

而对于我们所要求的最速曲线的问题，其实就是算出，

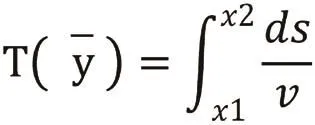
所对应的极小值，其中，

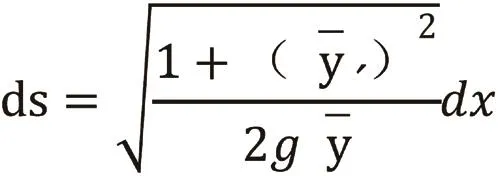
当我们把它写成一种更为一般的形式时，我们所求泛函即为：

该式被称作单宗量Euler方程[2]，同样的我们也能更为明了地理解变分的原理，对比两式后我们发现在泛函取得极值时（或者说系统趋于稳定时）与我们转化为函数极值问题得到相同的被积函数的形式，就可以更加深入地了解变分的原理。当然，凡事总是由一及多，由之前所推得的单宗量Euler公式，不难将其衍生到s个广义坐标上去，容易得到：

此时，系统为s个自由度，被积函数变成了L（qα，qα'；t）（α=1、2、3……），上式也就变成了保守了体系下的Lagerange方程。

当我们分析整个过程的时候不难发现，我们的逻辑顺序由自变量的变分出发，到函数变分，最后作用于泛函I的变分，而对于被积函数F的变分，δF=F(y+εξ，y'+εξ'；x)-F(y，y'；x)

此时的泛函S（qα，qα'）也就是我们定义的Hamilton作用量，确定泛函S的极值问题，就是最小作用量原理，有时也泛称为变分原理，那么这也是由数学向分析力学的一种延伸。

3.约束

当然至此，我们还忽略了一个十分重要的问题，那就是任何实际的问题都存在约束f（qα，qα'；t）=0，那么这个约束的意义[2]是什么呢？通俗地讲就是给我们假想的这种广义坐标或者说广义速度的变化给了限制，以虚功原理为例，假定在一管内，一静止小球，在理想约束的条件下我们假想一个虚位移δr时，δr只可能沿着x方向，不可能有y方向的分量，原本在没有约束的条件下我的δr可以是任意的，但当约束条件存在时，我的虚位移的变化变少了（更为科学地表述应当是自由度的减少），并且只能沿着特定的方向（即约束许可的轨迹）。同样的对比虚功原理与达朗贝尔原理，从理论上讲是对于静力学问题的虚功原理和动力学问题的达朗贝尔原理，分析其本质上的原理是没有能量的输入。

而至于说对于变分法的另一种形式的理解，假定我们所取的u（y，z；x）和v（y，z；x）在其本质上可以为

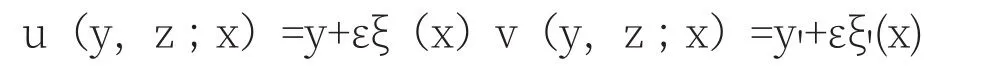
由于ξ（x）的函数形式和ε的取值是任意的，所以u，v也可以是x，y，z的任意函数，当然在讨论到泛函极值的问题是，ε为一个无穷小量，u和v在此时也就趋近于y和y'了。

4.结语

本文在阐述变分的原理时，以数学原理入手，从数学本身的角度来表述对于变分原理的看法，从对泛函极值的分析，转化为我们所熟悉的函数取极值的问题，以此继续在泛函取极值的情况下（转化的函数取极值）推导出单宗量的Euler-lagrange方程，以此为基础，考虑s个广义坐标下的Lagrange方程，并考虑对于被积函数的变分从而引入的Hamilton原理，在取得泛函极值的情况下的最小作用量原理，并结合变分原理表达对于虚功原理与达朗贝尔原理的认识。