增强型投影双胞支持向量机设计

郑世平,席文飞,王 梁

(1.内蒙古电力(集团)有限责任公司,内蒙古 呼和浩特 010020;2.华中科技大学材料科学与工程学院,湖北 武汉 430074)

0 引言

支持向量机[1](support vector machine,SVM)是一类基于核理论的学习模型。相对于神经网络,SVM 基于最大间隔思想,引入正则化技术,进而实现了模型的结构风险极小化准则。通过求解二次规划问题,它拥有全局最优解。同时,SVM 在处理小样本数据上性能卓越,因而受到了学术界与工业界的青睐,且已被成功应用到各大领域,比如图像识别、信号分析、故障检测、医学诊断等。然而,在处理异构数据分布学习任务上,SVM 的学习性能受到了较大的影响。为解决此问题,Jayadeva 等[2]在机器学习期刊TPAMI 上提出一种全新的双胞支持向量机(twin support vector machine,TWSVM)模型。相对于原始的SVM,基于非平行思想的TWSVM 模型[2]在处理异构数据问题上表现出卓越的泛化能力。因此,TWSVM 得到了国内外很多学者的关注,并后续提出了很多优秀的模型。例如双胞界限支持向量机(twin bound support vector machine,TBSVM)[3]、最小二乘双胞支持向量机(least squares twin support vector machines,LSTSVM)[4]、半监督近端向量机(manifold proximal support vector machine,MPSVM)[5]、多标签双胞支持向量机(multi-label twin support vector machines,MLTSVM)[6]、非平行支持向量机(nonparallel support vector machines,NPSVM)[7]等支持向量机模型。

投影双胞支持向量机(projection twin support vector machine,PTSVM)[8]是近年来被提出的一个非平行学习分类方法,拥有优秀的泛化能力。然而,PTSVM 模型的对偶问题存在矩阵求逆运行,加重了模型的训练负担。此外,矩阵求逆也将导致PTSVM 模型的不稳定性。为此,受NPSVM 模型[7]启发,提出一个新的增强型投影双胞支持向量机模型(improved projection twin support vector machine,IPTSVM)。该模型旨在寻找一对最优非平行投影方向,使得新投影空间的每个投影上,同类别的样本点尽量聚集在类内投影中心附近;另一方面,其他类样本尽量远离当前类别中心。在IPTSVM 模型中,使用等式约束对类内样本的损失函数进行了重构。然后,为提高模型稳定性,正则项被引入IPTSVM 模型。相对于PTSVM 模型,IPTSVM 模型对偶问题不再有矩阵求逆,进而提高了模型的训练效率。

1 投影双胞支持向量机回顾

本文符号约定如下:所有的向量都为列向量;上标“T”表示转置;I表示单位矩阵;0 和e分别表示全0 向量和全1 向量。

针对n维实数空间Rn的二分类学习任务[1],给定训练数据集:

式中:l为训练数据集规模;xi为在Rn空间中的第i个训练样本点,xi∈Rn;yi为xi所对应的类别输出,yi∈{-1,+1}。

记矩阵A和B分别为正类和负类样本集,记I1和I2分别为属于正类和负类的样本集合索引,其规模分别为l1和l2。

采用PTSVM 模型[8]构造如下二次规划问题:

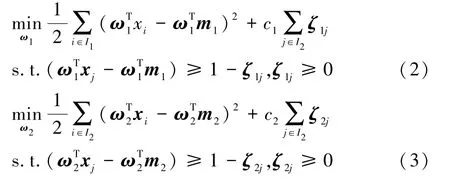
式中:c1、c2为模型的罚参数,c1≥0,c2≥0;ζ1和ζ2为样本的松弛变量,用于度量样本犯错程度;m1为正类样本中心,;m2为负类样本中心,。

为简化问题,分别定义正类和负类的类别散度矩阵:

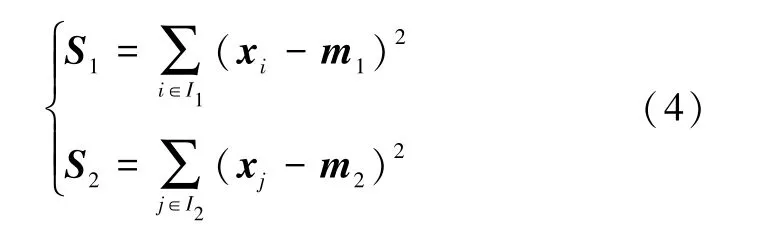
则问题(2)和问题(3)可转换为如下的矩阵形式:

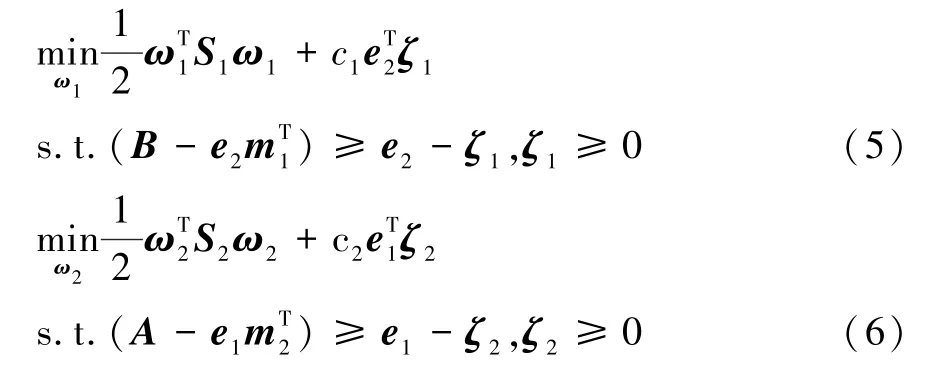
为求解式(5)和式(6)的最优解,将其转换为对偶问题:

求得对偶问题(7)和对偶问题(8)的最优解和,可根据式(9)、式(10)求得原始问题(5)和原始问题(6)的解:

2 增强型投影双胞支持向量机原理

由式(7)和式(8)可知,对偶问题中的Hessian 矩阵存在运算量较大的求逆操作。这将导致PTSVM 模型[8]的训练效率较低,且并不适合处理大规模学习问题。为此,受NPSVM 模型[7]启发,提出了新的IPTSVM 模型。IPTSVM 模型的核心思想是,旨在寻找一对最优的非平行投影方向w1和w2,使得新投影空间的每个投影上,同类别的样本点尽量聚集在类内投影中心附近;另一方面,其他类样本尽量远离当前类别中心。

为度量样本点与类别中心的偏移量,定义如下投影函数:

式中:k为1 或2。

为每个类别分别构造如下的经验风险函数:

式中:c1、c2为惩罚参数,用于调节损失函数式(12)和式(13)中各项损失的权重,c1>0,c2>0。

为度量类内散度,分别为正类和负类样本引入松弛变量η1和η2,即类内样本点离类中心越远该松弛变量就越大,反之亦然。为此,结合经验风险函数式(12)和式(13),IPTSVM 的模型可表示为:

为提高模型的泛化能力,在IPTSVM 模型中引入Tikhonov 正则项,用于控制模型的复杂程度。进一步,IPTSVM 模型的原始优化问题可表示为:

式中:λ1、λ2为正则项权衡参数,用于调节损失函数和正则项权重,λ1>0,λ2>0。

针对IPTSVM 模型的正类优化问题(17),给出详细的几何解释。

①第1 项和第1 个约束条件使用了最小二乘法损失函数,实现正类样本的经验风险函数。对于偏离类别中心的正类样本点xi,通过引入松弛变量η1i度量其误差。极小化该项,在新的投影空间中,期望所有正类样本能聚在正类中心附近。

②第2 项和第2、第3 个约束条件使用了Hinge 铰链损失函数,实现负类样本的经验风险函数。极小化该项,在新的投影空间中,期望负类样本尽量地远离正类别中心;如果距离小于1,则通过引入松弛变量来度量其误差。d1(xj)越大,则代表负类样本与正类中心的间隔越大,那么模型的泛化能力将会越强。

IPTSVM 模型的几何解释如图1 所示。

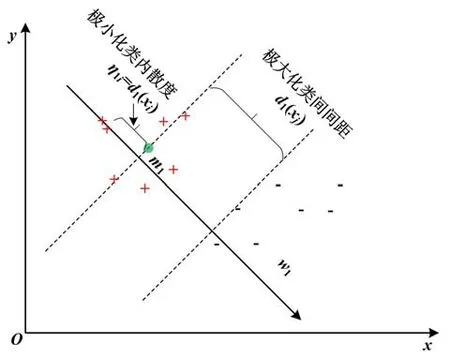
图1 IPTSVM 模型的几何解释Fig.1 Geometric interpretation of the IPTSVM model

3 模型优化与求解

为简化计算,针对模型求解优化问题(16),首先定义各类数据到类别中心mk的偏差矩阵:

则优化问题(16)与优化问题(17)可进一步转换为如下的矩阵形式:

由于优化问题(16)与优化问题(17)具有类似形式,篇幅有限,下文只关注优化问题(16)的求解。优化问题(17)可采用类似的方法。考虑优化问题(16)的Lagrange 函数:

式中:α1、β1、γ1为Lagrange 乘子。

根据Wolfe 对偶理论[1],对L(ω1,η1,ζ1,α1,β1,γ1)关于变量ω1、η1、ζ1、α1、β1、γ1求偏导,并令它们的偏导为0。由此可得如下karush-kuhn-Tucker(KKT)充分必要条件:

由此可得:

将上述参数代入L(ω1,η1,ζ1,α1,β1,γ1),并结合KKT 条件(23)和KKT 条件(30),可得优化问题(20)的对偶问题:

对偶问题(34)的最优解(α1,β1)可由二次规划(quadric programming,QP)工具包求解。当得到最优解(α1,β1)后,可根据式(31)得到原始问题(16)的最优解ω1。

同理,针对优化问题,可推得其对偶问题:

当得到问题的最优解(α2,β2)时,可根据式(37)得到原始问题的最优解ω2。

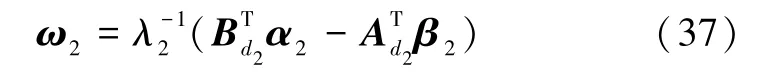
对于新样本x的预测,其类别的判别依据如下决策函数:

4 试验结果分析

所有试验均以Matlab 2017a 为软件平台,以Intel Core i3 处理器、8 GB 内存的计算机为硬件平台。为验证本文所提的IPTSVM 模型的有效性,以分类准确率和训练时间为指标,选取来自加州大学尔湾分校(University of California Irvine,UCI)的9 个公共数据集,对SVM[1]和PTSVM[8]进行性能对比试验。SVM、PTSVM 和IPTSVM 的优化问题都采用Matlab 二次规划求解器quadprog 求解;PTSVM 的Hessian 矩阵求逆采用求逆‘/’运算符。选择径向基函数(radial basis function,RBF)核作为非线性学习核函数:k(x1,x2)=。其中,φ为核参数。为简化寻参过程,试验中设置PTSVM 的参数c1=c2=c、IPTSVM的参数c1=c2=c和λ1=λ2=λ。模型的选参使用十折交叉验证法[1]。参数包括:SVM 模型中的c;PTSVM 模型中的c、IPTSVM 模型中的c、λ、非线性RBF 核参数φ,选参范围为{2-6,2-5,...,25,26}。

表1 给出了SVM、PTSVM 和IPTSVM 模型在UCI数据集的分类准确率。

表1 SVM、PTSVM 和IPTSVM 模型在UCI 数据集的分类准确率Tab.1 Classification accuracy of the SVM、PTSVM、IPTSVM models in UCI dataset %

表1 中,最好的分类准确率以加粗标识。试验结果表明:本文所提出的IPTSVM 模型,拥有与原PTSVM模型相近的分类性能。在9 个UCI 数据集中,有6 个数据上分类性能超过PTSVM。例如在Cancer 数据集上,相对于PTSVM 为96.13%,IPTSVM 的准确率为96.81%。从分类稳定性上看,本文所提的IPTSVM 模型在大部分的数据集的十折分类方差都比PTSVM 模型低。这主要归因于正则项的引入控制了IPTSVM 模型的复杂度,可防止模型过拟合,进一步提高了IPTSVM 模型的稳定性。

图2 给出了SVM、PTSVM 和IPTSVM 模型在UCI数据集的平均学习时间。

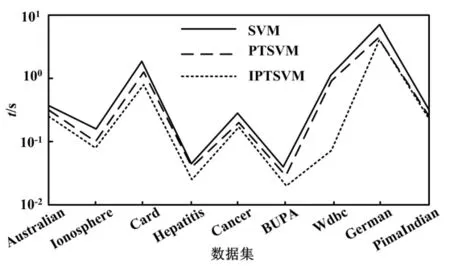
图2 SVM、PTSVM 和IPTSVM 模型在UCI 数据集的平均学习时间Fig.2 Average learning time of the SVM、PTSVM、IPTSMVM models in UCI dataset

试验结果表明:本文所提的IPTSVM 模型的训练时间最短,其次是PTSVM,而SVM 训练时间最长。由于PTSVM 在构造二次规划问题时,需要对Hessian 矩阵进行求逆运算,大大增加了训练负担;而IPTSVM 模型的改进使得其对偶不存在求逆,进而提高了模型的学习效率。此外,SVM 通过构造一个优化问题来求解分类超平面,而PTSVM 和IPTSVM 则继承了非平行学习范式,将较大规模的问题分解为较小规模的问题求解,使得它们的学习效率相对SVM 更高。

上述试验结果验证了IPTSVM 模型的有效性。

5 结论

PTSVM 模型的求逆运算加重了模型的训练负担,容易引起模型的不稳定性。为此,本文提出了新的增强型投影双胞支持向量机,即IPTSVM。该模型旨在寻找一对最优非平行投影方向,在新的投影空间中,使得在每个投影上同类别的样本点尽量聚集在类内投影中心附近,而其他类样本尽量远离当前类别中心。该模型有效地避免了矩阵求逆问题,提高了模型的训练效率。模型中的正则项提高了模型的泛化能力,保障了模型解的稳定性。UCI 公共数据集的仿真结果验证了IPTSVM 模型的有效性。