基于机器学习算法的冬小麦始花期预报方法

徐 敏，赵艳霞，张 顾，高 苹，杨荣明

（1.江苏省气候中心，南京 210008；2.中国气象科学研究院，北京 100081；3.江苏省气象服务中心，南京 210008；4.江苏省植物保护植物检疫站，南京 210036）

0 引 言

小麦赤霉病防治时期不同，用药效果差异较大，始花期是其最佳防治期。在小麦扬花6.0%～37.5%时施药，病指防效可达72.0%～79.0%；过早或过迟用药，病指防效均低于 45.0[1-4]。赤霉病是威胁小麦产量和品质的重大流行性病害，而且已成为小麦生产可持续发展的重要影响因素之一[5-6]，因此，开展小麦始花期预报研究对赤霉病精准防治具有重要意义[7]。

以意大利山洪预警系统为例，欧盟一些国家所建设的山洪预警系统主要包括三个方面的内容：一个可视化的便于操作的平台；具有不同功能的模块，包括服务器优化计算分析模块，实时数据接收和存储模块，雷达数据管理和处理模块；综合形成预警信息的决策信息生成系统。在监测预警系统建设中，欧盟非常重视基础工作，例如建立相对比较详细的自然和社会经济数据库，开展降雨与流量的耦合监测和分析，进行山洪灾害事件现场调查和数据整编入库等。

两种针刺工艺路线主要区别在于进入预刺之前，PPS含基布滤料会作为夹心层铺在净气面（底层）上，然后迎尘面 （面层）纤网会铺在PPS基布上，形成三层结构，PPS无基布滤料在进入预刺之前不会有放卷PPS基布在两层纤网中间，针刺环节只会发生纤维与纤维之间的抱合。由于无基布滤料没有基布作为加强层，在针刺工艺参数设置上，会适当降低针刺密度，增加针刺深度，增加针刺机工作辊速度，增加梳理机喂入量，以降低对纤维的损伤，同时保障纤维之间的抱合力。

根据冬小麦生长发育与气象条件之间的关系及自身的生理特性，国内外学者针对其生育期监测预测开展了系列研究，方法主要有 3类：一是通过冬小麦生育期模型进行预测，二是通过卫星遥感监测资料提取冬小麦关键物候期，三是通过统计预报法或经验进行预测。生长模型充分考虑了冬小麦生长发育的生理过程，因此在本地化应用之前需要大量的试验数据为基础，对敏感参数进行校正，还要针对研究区域的气候特征和冬小麦品种等，调试出不同品种的模型参数，而冬小麦品种繁多，所以作物模型在实际应用中还存在一定难度和限制[8]。遥感技术的发展为大面积监测作物关键物候期提供了新的手段[9]，如2016年杨琳等[10]利用MODIS NDVI数据提取了冬小麦返青期、抽穗期、成熟期的普遍期，由于采用动态阈值法提取物候期需要人为设定阈值，并且没有考虑阈值的空间变化，会影响物候提取的精度。20世纪80年代起，中国农业气象工作者在作物发育期预报方面总结了积温法[11]、温湿法[12]等统计预报方法，还总结了平均间隔法、物候学法等经验预测法，统计方法和经验法较前 2种方法相对简单易算，但由于影响生育期的多重因子之间存在较为复杂的非线性关系，在一定程度上限制了预报精度的提升。前人的研究为冬小麦生育期预报研究奠定了基础，但在预报精度、实际应用可操作性等方面还有待改进，而且专门针对冬小麦始花期预报方法的研究尚未见详细报道。因此，本文将利用机器学习算法在客观度量各预报因子重要性的基础上，考虑因子间的非线性作用，建立始花期预报模型，拟进一步提高预报精度，且具有可行性。

1)MOR方案和MY方案的模拟的结果在雨带的走势上与实况十分吻合,都成功模拟出东北—西南走势的雨带,但在雨带的位置上,MOR方案模拟的效果要更接近实际情况;对于最大累积降水量的模拟,MOR方案和MY方案的最大累积降水量都超过实际情况,但相比于MOR方案,在最大累积降水量的模拟上,MY方案效果与实际更为接近。

结合上述“地平线欧洲”和“地平线2020”比较分析，可以看出“地平线欧洲”的四大重大转变同中欧科技合作的共识契合度高，是支持未来中欧科技合作的有力政策执行工具。对欧科技合作中，中国科技界可以在中欧科技合作共识基础上，结合中国科技发展自身利益需求，充分利用“地平线欧洲”这一欧盟科技政策执行工具，特别是该计划下的资金、资源和政策，推动和实现双方在共同利益领域互利互惠的科技合作。启示建议如下：

1 资料与方法

1.1 数据资料

冬小麦生育期观测资料和气象观测资料均来自于江苏省气象局，其中，江苏省冬小麦生育期观测资料普遍始于20世纪80年代初期，观测站点共10个：昆山、如皋、兴化、大丰、盱眙、滨海、淮安、沭阳、赣榆、徐州。冬小麦播种期、出苗期、三叶期、分蘖期、越冬期、返青期、起身期、拔节期、孕穗期、始穗期、抽穗普遍期、始花期、开花普遍期、乳熟期等，均由专业的农业气象技术人员按照《农业气象观测规范 冬小麦》（QX/T 299-2015）观测所得，一般发育期在下午观测，开花期在上午观测，其中抽穗与开花期每日观测，穗期和花期是以观测的总株（茎）数进入发育期的株（茎）数所占的百分率确定，当第一次进入开花期的株（茎）数百分率≥10%时，该日期记录为始花期。

气象数据为各站点生育期观测年份对应的逐日气象观测资料，主要包括平均气温（℃）、≥0℃活动积温（℃）、最低气温≤0℃的累计日数（d）、降水量（mm）、降水日数（d）、日照时数（h）、日照百分率≥60%的日数（d）。

2.3.2 基于BP算法建立始花期预报模型

在大数据时代的背景下，机器学习算法在预测模型构建及特征变量重要性评估等方面开始凸显优势[13]，已成为现代农业气象科研和业务发展的重要工具[14]，如随机森林、神经网络等，这些算法不要求样本数据满足特定的分布形式，具备解决高维变量的能力[15]，已在玉米发育程度自动识别[16]、大豆精细识别[17]、梨花花期预报[18]、油菜花期预报[19]、赤霉病病穗率预测[20]中进行了较好地应用。本文采用随机森林算法、反向神经网络算法、多元线性回归算法分别建立冬小麦始花期的预报模型，并对模型精度进行较为全面的比较。研究结果可为优选较合适的算法建立冬小麦始花期预报模型提供依据，同时也为进一步提高预报精度提供了新思路。

1.2 资料预处理和区域划分

始花期数据采用日序法转换为数值型数据，即1月1日、1月2日、1月3日……分别为1、2、3……，其余类推。由于江苏南北跨度较大，气候条件的差异影响着始花期的迟早，按照气候相似性原则，结合农业区划，以淮河灌溉总渠和长江为界线，分为苏北、苏中、苏南3个区域，文中搜集到10个观测站点，按照所在地区，徐州、赣榆、淮安、沭阳、滨海可作为苏北地区的代表站点，大丰、如皋、兴化、盱眙可作为苏中地区的代表站点，昆山可作为苏南地区的代表站点。

1.3 方法介绍

1.3.1 随机森林算法

药士歉然一笑，回道：“小姐错了，孕者脉相为滑脉，即脉往来流利，应指圆滑，呈连珠滚玉盘之状，并非是两个脉。此女子脉相特殊，体内如有两颗心脏，同跳同止，频率一致，但她的心子，确实只有一颗，这种怪相，我也从来未曾遇见过。”

随机森林（Random Forest，RF）算法是以决策树为基分类器的一个集成学习模型｛H(x,θk);k=1,…｝，｛θk｝表示独立同分布的随机变量，输入特征变量X时，每一棵树只投一票给其认为最佳的分类结果。所谓决策树[21]，是单个分类器，是一种从无次序、无规则的训练样本中推理出决策树表示形式的分类规则的方法，相当于一种布尔函数。RF的分类结果由每棵树投票中得票数最多的类确定[22]，最终分类决策模型见公式（1）：

式中H(x)表示随机森林模型；hi(x)表示每个决策树分类器；Y为目标变量，即始花期；I(hi(x)=Y)为指示性函数，采用R语言进行编程计算。

随机森林的样本数据集由影响始花期的气象因子、播种期日序、始花期日序构成。首先采用随机抽样的方法，按照一定比例确定训练集和测试集；然后通过自助法从原始样本集采样得到构建N棵树所需的N个子集，每次未被抽到的数据称为袋外数据，用来进行内部误差估计和特征变量重要性评价。选用“精度平均减少值”，含义等价于“均方差增加值”（Increase in Mean Square Error，IncMSE）[23]作为特征变量重要性的评价指标，IncMSE值越大，说明该变量越重要，反之则相对不重要。通过特征变量重要性排序，可筛选出对始花期影响较大的变量，删除一些和始花期无关或者冗余的特征变量，从而简化特征数据集，使得预测模型更精确。

1.3.2 反向神经网络算法

反向传播（Back Propagation，BP）神经元网络算法是基于 Delta 学习规则[24]，利用梯度搜索技术，通过反向传播来不断调整网络的权值和阈值，最终实现网络的实际输出与期望输出的均方差最小化。文中采用 3层拓扑结构，即含输入层、隐含层、输出层，其中隐含层节点数采用经验公式法[25]根据输入层因子个数来设定，训练过程中，设置模型收敛误差为0.001，最大迭代次数为1 000次。

2.3.3 基于多元线性回归算法建立始花期预报模型

多元线性回归算法[26]（Multiple Linear Regression，MLR）是根据自变量的取值来预测因变量的取值。文中采用“步进法”，即需对方程中引入的每个新变量进行检验，纳入自变量的显著性概率P值需小于0.05，剔除自变量的概率P值需大于0.1，以此类推，直至方程稳定。采用“德宾-沃森”法检验自变量之间的自相关性，若检验值接近0或4时，则存在自相关；若越接近2，则不存在自相关；采用容差的倒数（VIF）诊断自变量之间的共线性程度，0＜VIF＜10、10≤VIF＜100、VIF≥100分别表明不存在多重共线性、存在较强的多重共线性、存在严重的共线性问题。对整个回归方程采用F检验，若F值对应的Sig值小于0.05，则表明建立的回归方程有效。

以转归为因变量。经单因素Logistic回归分析，在α=0.10水平上，年龄、性别、肺部疾病史、原患疾病、ILD发生时间共5个指标有显著性影响，可能作为吉非替尼致ILD死亡的危险因素。见表1。

采用决定系数（Coefficient of Determination，R²）、均方根误差（Root Mean Square Error，RMSE）和预报准确率（Ratio of Accuracy，RA），对始花期预报模型的精度进行评价，其中决定系数R2是用来衡量预测模型对观测值的拟合程度，它的值越接近1表明模型效果越好。

式中n为样本总数，yai、ysi分别表示实际始花期和模拟始花期，、分别表示实际始花期平均值和模拟始花期的平均值。式（4）中Nj表示偏差天数为j天的年数，j表示始花期模拟值与实际值的偏差天数（j≤3 d）。

2 结果与分析

2.1 冬小麦始花期基本特征

从表1可见，10个站冬小麦始花期历史最迟与最早相差天数都在21 d以上，不同区域间始花期存在差异，苏北、苏中、苏南地区的平均始花期日序分别是120、115、110 d。标准差大小可以表示始花期的离散度，苏北和苏中地区始花期的标准差都是 5～6 d，苏南地区始花期标准差是7 d。有观测记录以来历史极端最早始花期是2002年4月5日，发生在昆山站，历史极端最迟始花期是2012年5月13日，发生在沭阳站。各站冬小麦始花期存在年际波动，且标准差较大，所以有必要通过建立预报模型对始花期进行预报。从总的变化趋势来看，滨海、淮安、昆山、如皋有较明显的提前趋势，线性倾向率分别为 4.3、3.2、3.2、2.6 d/(10 a)；徐州、赣榆、大丰略有提前趋势，主要集中在 2010年以来；沭阳、兴化、沭阳变化趋势不明显。采用偏度和峰度检验法[26]，对各站历年始花期出现的时间序列进行正态分布性检验，首先计算出始花期时间序列的偏度、偏度标准误差、峰度、峰度标准误差，然后计算相应的Z评分（Z-score），即偏度Z-score=偏度值/标准误差，峰度Z-score=峰度值/标准误差，在α=0.05的检验水平下，发现10个站的偏度Z-score和峰度Z-score均在±1.96之间，则表明各站冬小麦始花期资料符合正态分布的特征，说明可以通过建立多元线性回归模型对始花期进行预报。

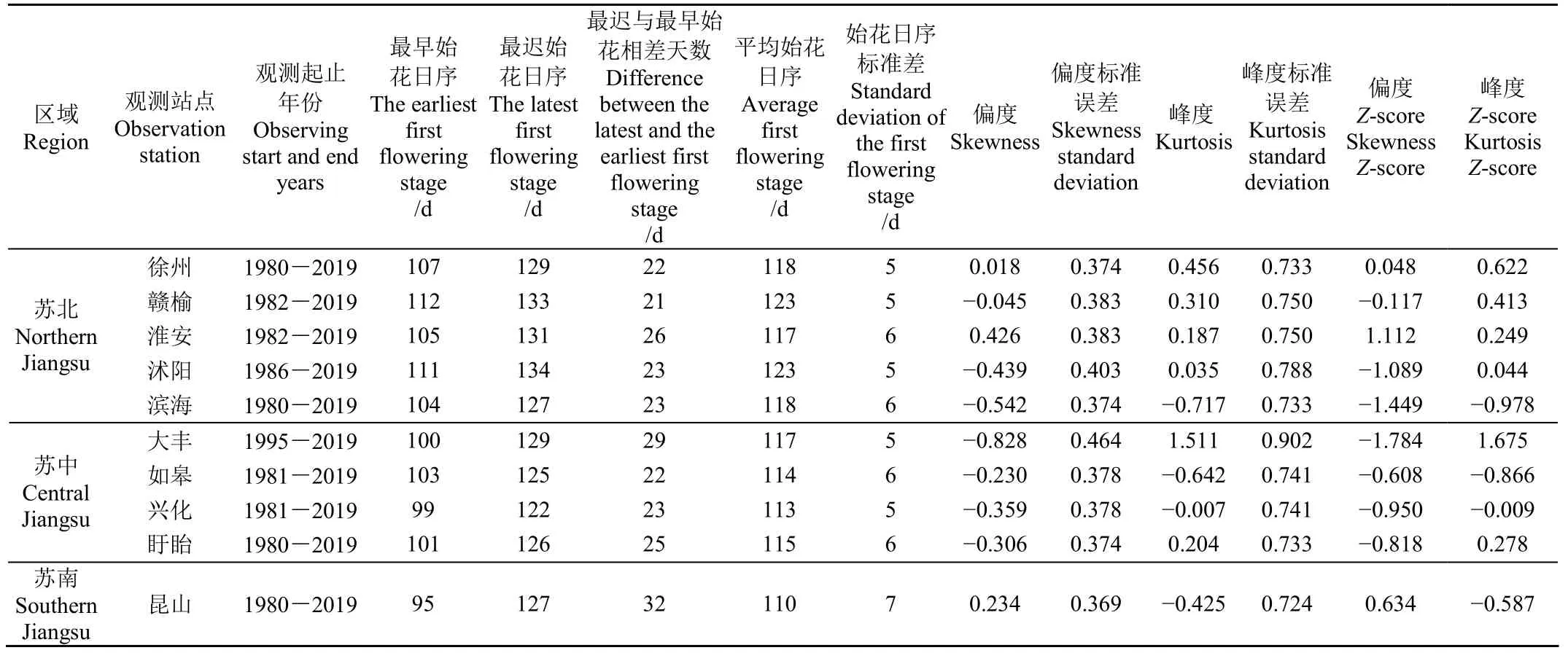
表1 冬小麦始花期观测时段和特征信息Table 1 Observation period and characteristic information of the first flowering stage of winter wheat

2.2 影响始花期的预报因子筛选及其评价

冬小麦在生长过程中需要具备一定的热量、光照和水分，光温水条件的匹配程度影响着生育进程的快慢，因此，为了筛选出对始花期有影响且符合生物学意义的气象因子，将温度、降水、日照 3类因子均作为预报因子的初选因子。考虑到所选预报因子距离实际始花期应有一定提前量，因此预报因子的统计终止日期设定为 3月末，选用的具体气象因子见表2。利用建立的始花期预报模型在4月1日对各站的始花期进行预测，由于始花期历史极端最早日期是4月5日，因此所建立的预报模型可以提前 5 d进行预测；最迟始花期中兴化站日期最早，为5月2日，预报模型最早可以提前32 d。另外，考虑到播种期的早晚对生育进程也会有一定影响，因此将播种日序（记为D）也作为预报因子。

表2 影响冬小麦始花期的气象因子Table 2 Meteorological factors affecting the first flowering stage of winter wheat

以27个气象因子（表2）和播种日序作为RF算法的输入向量，树节点预选的变量个数Mtry根据28个预报因子总数分别设定为7、8、9、10、11，决策树棵数Ntree设定为600，以始花期为输出向量，利用RF算法分别对10个站点的输入向量进行重要性排序，计算各特征向量的IncMSE。在成百上千次的机器学习过程中，并非每一次计算出的变量重要性排序结果都完全一致[27]，此时可通过计算 IncMSE平均值来避免个别预报因子排位靠前的偶然性。对每个Mtry参数各计算50次，则各站需计算250次，针对苏南、苏中、苏北3个区域，将各区域内对应站点的IncMSE进行平均，得到IncMSE区域平均值，以此进行各区域预报因子的重要性排序，筛选出重要特征变量再进行 RF建模可降低不重要变量对模型精度的干扰。

1.3.4 模型精度评价方法

从图1可见，苏南、苏中、苏北地区影响冬小麦始花期的因子中排在前列的重要因子基本一致，排在前五位的均为温度类因子，分别为上年12月—当年3月日均温≥0 ℃活动积温、上年12月—当年3月平均气温、上年12月—当年3月最低气温≤0 ℃的累计日数、当年3月平均气温、上年12月—当年2月日均温≥0 ℃的活动积温，这5个因子的IncMSE累计占比在苏南、苏中、苏北地区分别为64.0%、59.3%、64.8%，说明这5个因子对始花期的影响作用最为明显。选取苏南、苏中、苏北地区代表站点，即以昆山、如皋、徐州为例，计算始花期与各预报因子的相关系数，发现以上 5个因子与始花期存在高相关性，上年12月—当年3月日均温≥0 ℃活动积温、上年12月—当年3月平均气温、上年12月—当年2月日均温≥0 ℃的活动积温、当年3月平均气温与始花期呈现显著的反相关，相关系数绝对值均在0.643以上，通过了0.001的显著性检验，其中上年12月—当年3月日均温≥0 ℃活动积温与始花期的相关性最高，相关系数分别为−0.834（昆山）、−0.839（如皋）、−0.781（徐州），上年12月-当年3月最低气温≤0 ℃的累计日数与始花期呈现显著的正相关，相关系数分别为0.790（昆山）、0.742（如皋）、0.643（徐州），这5个因子与始花期的相关系数普遍高于其他预报因子。当IncMSE值出现明显拐点，可将出现拐点前的特征变量确定为相对重要的变量，可见苏南、苏中、苏北地区降水类和日照类因子对始花期影响的重要性均明显弱于温度类因子，从相关系数数值上也反应出了 3类预报因子间同样的重要性差异特征。结合冬小麦生育期生长发育特点，出苗、分蘖、越冬、返青、拔节、孕穗等生育阶段，热量条件都是最为重要的外界环境因子，温度过低会抑制其生长甚至造成冻害，温度偏高则会使得发育期提前。

大部分地区上年12月日照百分率≥60%的日数和当年1月日照百分率≥60%的日数与始花期呈弱的正相关，这可能与该阶段小麦处于春化阶段有关，春化阶段需要有一定的低温时段，这样才有利于完成营养生长向生殖生长的过渡，若日照时数较多往往意味着天气晴朗，气温通常会相对高一些，则完成春化的时间相对稍长一些，则易推迟抽穗开花，3月日照百分率≥60%日数与始花期均是呈弱的负相关，因为此时冬小麦处于光照阶段，若日照时数多，则利于光合产物积累，易使抽穗期提前，则始花期也相应提前。总体来看始花期与日照长短的相关性明显弱于气温因子与始花期的相关性，这与品种特征有关，因为江苏大部分地区种植半冬性小麦、小部分地区种植春性品种，半冬性品种对日照长短的反应大多数属于中等型，而春性品种则属于反应迟钝型，即日照时数多少主要影响光合作用，对发育进程的影响相对弱一些[28]。

不同时段降水量与始花期的相关性不同，这与冬小麦生长过程中的水分需求特性总体是一致的[29]，12月的降水量与始花期呈弱的负相关，因为此时正值播种出苗期，水分需求量较大，充足的水分利于播种出苗，反之若水分不足则易出现旱情，使得出苗不齐，生长放缓；1—2月冬小麦处于越冬期，需水量小，而此时江苏也通常处于少雨季，因此该阶段的降水量与始花期几乎不存在相关性；3月的降水量与始花期呈弱的正相关，此时进入春季，暖湿气流开始活跃，降水开始增多，若降水过多易导致湿渍害，尤其是里下河地区，地势较为低平，更容易出现湿渍害，影响根系生长，使得小麦发育延迟。

2.3.1 基于RF算法建立始花期预报模型

从IncMSE来看，苏南、苏中、苏北播种期的重要性分别排在第7位、第23位、第11位；从相关系数来看，各地区播种期与始花期基本呈弱的正相关，南部地区的相关性稍高于北部地区，这可能与播期早晚有关，苏南地区播种期以11月上旬居多，要晚于苏中和苏北地区，而苏南地区始花期通常又早于其他 2个地区，所以苏南的播种期对始花期的影响相对要稍微大一些。

直接接触式膜蒸馏实验结果如图 1和图 2所示。由图 1可知，膜通量随着实验的进行逐渐减小，最后膜通量趋于零。这是因为随着原料液中的水进入透过侧，进料侧盐溶液的浓度逐步增大，盐溶液的蒸汽分压不断减小，导致膜两侧的蒸汽压差下降直至趋于零。与其他膜相比膜1的通量9 h时达到最低点之后膜通量又开始上升，图 2中膜 1的盐截率在500 min前稳定在0.999，从500 min后逐渐下降至0.9左右。所以，大约从9 h时盐截率下降，膜失去部分疏水性，膜通量上升。

综合考虑IncMSE和相关系数，结合冬小麦生育期生物学特性，筛选出各地区始花期的关键预报因子（见表3），其中温度类因子11个、降水类因子3个、日照类因子4个。同时兼顾人为播种早晚的影响，所以仍保留播种期这一影响因子。

2.3 基于3种算法的始花期预报模型构建和精度对比

操动机构由手动或者电动的方式完成合闸，而合闸能量可以转变成电磁能和弹簧的位能及重力位能等，可以促动断路器的动作。提高断路器结构与传动机构的机械性能，一旦机构发生故障，就会使断路器发生拒动，而电磁操动机构是由螺管电磁铁执行动作，电磁铁线圈电压与电流可以说是影响电磁铁处理能力重要的因素[1]。

以表3中筛选出的影响始花期的重要特征变量为输入向量，树节点预选的变量个数Mtry根据预报因子总数19而分别设定为 4、5、6、7、8，决策树棵数Ntree设定为600，始花期为输出向量，利用RF算法分别建立10个站的始花期预报模型，为了避免高相关模型的偶然性，均重复建模50次，每次建模均随机抽取3/4的样本作为训练样本、1/4的样本作为测试样本。各站建立的50个始花期预报模型，其模拟值与实际始花期的相关系数存在差异，由于训练样本的相关系数均很高，基本都在0.96～0.98之间，所以根据测试样本相关系数的高低来挑选RF模型，测试样本相关系数最高的RF模型称为最优模型，由于参数Mtry设定了5个值，因此每个参数值将得到一个最优RF模型，分别记为RF1、RF2、RF3、RF4、RF5，将筛选出的5个最优模型进行等权重集成，在一定程度上可以减少模型的随机误差和高相关的偶然性[30]。

表3 筛选出的影响冬小麦始花期的重要特征变量Table 3 Important characteristic variables affecting first flowering stage of winter wheat

受篇幅所限，以苏南、苏中、苏北的代表站点为例，图2可见，无论是单个最优模型的模拟值还是最优模型集成后的模拟值，均很好地模拟出了近四十年实际始花期的波动趋势，波动幅度与实际始花期在极端年份存在一定差异，即对于始花期明显提前和推迟的极端情况，模拟幅度小于实际变化幅度。

另外，由于筛选出的温度特征量存在相互重叠的现象，因此在实际计算中尝试了选取不同温度特征量的组合进行建模，发现将表2中筛选出的11个温度因子全部放入时，预报精度相对高一些，这可能与RF算法本身有关。

经历了家道中落的鲁迅厌恶了周围熟悉的人群,为摆脱这种旧有的人事关系和改变自己的命运，1898年，鲁迅前往南京寻求别样的人生,并先后进入江南水师学堂、江南陆师学堂附设的矿路学堂学习。在此期间，学习的鲁迅接触到维新变法的宣传刊物《时务报》，作为热血青年的鲁迅，救国救民的壮志开始生根，受惠于维新变法派留学生的变法举措留学日本。就这样，鲁迅抱着寻求新知、拯救过敏的热情来到了东京。鲁迅进的第一所预备学校是东京弘文学院,并加入了革命团体浙学会，成为一个激进的革命者，且颇为勇敢。从剪辫子事件就可看出，在剪辫之后不仅毫无畏惧，还特地“断发照相”，以资纪念，并题了一首诗——自题小像，赠给友人许寿裳。诗云：

通常移动式筛分站上的输送机液压驱动滚筒结构有两种：一种结构是液压马达+联轴器(或者减速机)+滚筒，如图2；另一种是马达直接通过联接法兰和滚筒联接，如图3。但这两种方式都无法解决输送机轴向尺寸过大的问题，也有一种内藏式液压滚筒[2]，但这种滚筒损坏后维修较为困难。因此在第二种结构形式的基础上，采用特定的轴承和液压马达，设计了一种半内藏式液压马达驱动滚筒，如图4。既解决了输送机轴向尺寸过大的问题，在维修方面也比全内藏式液压滚筒简单方便。

基于BP算法的始花期建模步骤是：首先将筛选出的影响始花期的预报因子（表3）进行归一化处理，作为输入层；然后对影响因子数据集进行网络训练，隐含层神经元传递函数采用非线性变换函数—Sigmoid函数，该函数特点是本身及其导数都是连续的，因而在处理上十分方便，神经节点的变量个数Net根据预报因子总数19而分别设定为37、38、39、40、41，均重复建模20次，每次建模均随机抽取样本的 75%进行模型训练；输出层神经元传递函数采用线性函数 Purelin，训练函数采用Trainlm，随机抽取样本的 25%用于模型测试。计算各站建立的 20个始花期预报模型模拟值与实际值的相关系数，发现无论是训练样本还是测试样本，相关系数差异比较大，同样按照RF算法中的最优模型筛选思路，根据模拟效果的高相关系数筛选出每个神经节点下模拟效果最好的模型，由于参数Net设定了5个值，因此每个参数值将得到一个最优BP模型，分别记为BP1、BP2、BP3、BP4、BP5，将筛选出的5个最优模型进行等权重集成。

从图3可以看出，无论是单个最优模型的模拟值还是最优模型集成后的模拟值，均较好地模拟出了近 40 a实际始花期的波动趋势，但波动幅度均明显大于实际变化幅度，而且对于始花期较为极端的年份，不同最优模型之间差异也比较大，5个最优模型集成后的模拟效果总体好于单个最优模型。

1.3.3 多元线性回归算法

在利用多元线性回归算法建模时，若将表2中所有的因子直接作为自变量进行建模，则自变量之间易出现严重的多重共线性问题，而且计算量大、模型准确率偏低，因此在建模前，根据RF算法计算出的IncMSE值，将出现明显拐点前的特征变量作为多元线性回归中自变量的初选因子。建立的回归模型如下：

式中Y为冬小麦始花期，其下标为站名。

始花期预报模型（5）～（14）总体模拟效果均通过了F检验，自变量均通过了T检验，预报模型自变量个数≥2时，自变量之间的VIF基本都小于10，即不存在共线性问题。各模型始花期历史拟合值与实际值的相关系数在0.543～0.944之间，均通过了0.001显著性检验，其中昆山站和如皋站相关系数最高，分别为0.944、0.904，对始花期波动特征模拟效果相对较好；盱眙站和沭阳站相关系数最小，分别为0.592、0.543，对始花期极端低值模拟偏差比较大。模拟效果与入选的自变量密切相关，从各模型最终入选的自变量可以看出，均含有温度因子，尤其是上年12月－当年3月日均温≥0 ℃活动积温是最主要影响因子，昆山站入选的自变量有4个，个数最多，其次是如皋站3个，这2个站的德宾-沃森值均接近2，说明预报模型的自变量之间不存在自相关，其余站点的自变量个数仅有1～2个，这与“步进法”中严格的自变量筛选标准有关，当原来引入的解释变量由于后面解释变量的引入变得不再显著时，则将其删除，所以模型中最终只能保留对始花期影响显著的自变量。

其中公式（5）、（7）、（8）中Tave.winter和Tave.12前面的符号为正号，这与冬小麦生长过程中的生理特性有关，小麦在幼苗阶段需要通过一定的低温时期，即需要经过春化作用，才能正常开花，进而完成营养生长向生殖生长的过渡，是小麦发育过程中一个重要的质变过程[31-32]。公式（5）和（8）中Tave.winter是指冬季平均气温、公式（7）中的Tave.12是指12月平均气温，这2个因子都处于春化阶段，若平均温度高，说明低温时段相对偏少，则春化阶段需要较长的时间，则易导致开花期推迟。

2.3.4 3种算法的模拟精度比较

如果在中文检测不出结果，但该研究结果又是该论文的核心内容，则要考虑是否是直接从外文学术文献中翻译过来的。方法是将核心压缩出来的内容翻译成英文，语法和表达式并不重要，但对其中的关键词和数据翻译必须准确，翻译完成后，复制到谷歌(英文版)上搜索。该方法的准确率要看责任编辑的总结能力以及英语翻译能力。

教学查房是临床实践教学的一个重要环节，是医学生培养的必经过程。通过教学查房，留学生开始进入医生角色，深入临床实践。在肿瘤学教学查房中，教师应不断提升自身教学水平，应用适应于留学生特点的方式进行教学活动，鼓励学生积极参与、主动思考，培养学生综合能力，促进师生协作交流，完善教学中的不足，最终提高留学生教学质量。

通过计算决定系数（R2）、均方根误差（RMSE）、预报准确率（RA），比较3种算法下的始花期模拟精度。从表4可见，RF、BP、MLR算法下各站的R2分别在0.850～0.932、0.599～0.930、0.295～0.892之间，RF算法下R2明显整体大于其他2种方法，数值更接近于1，说明 RF算法下的模型对始花期波动趋势拟合度最好，MLR算法对不同站之间的趋势拟合度高低差异最大，对于同一个站点，R2数值高低排序为RF＞BP＞MLR；RF、BP、MLR算法下各站的RMSE分别在3.9～6.5 d、3.5～7.9 d、4.0～6.4 d之间，3种算法下的模型对始花期波动幅度的模拟均存在一定偏差，而且不同站点的偏差幅度有高有低，对于同一个站点，RMSE数值高低排序为BP＞MLR＞RF，即BP算法下总体的波动幅度模拟偏差更大一些；RF、BP、MLR算法下各站的 RA分别在76.5%～92.5%、60.0%～92.1%、40.0%～85.0%之间，对于同一个站点，RA数值高低排序为RF＞BP＞MLR，即 RF算法下模型预报准确率最高，大部分站点都在 85.0%以上，BP算法次之、大部分站点在82.0%以上，MLR算法仅有 3个站的预报准确率在82.1%～85.0%之间，其余均在 76.3%以下。因此，综合考虑3种算法下模型对始花期变化趋势、波动幅度、准确率的模拟能力，RF算法模拟精度最高，BP算法次之，MLR算法相对低一些。

表4 基于3种算法的冬小麦始花期预报模型模拟精度对比Table 4 Comparison of simulation accuracy of forecasting model of first flowering stage of winter wheat based the three algorithm

3 讨 论

预报因子的初步筛选是冬小麦始花期预报模型建立的基础，RF算法具有筛选重要特征变量的优势，得出的预报因子重要性排序与预报因子和始花期相关系数的高低相吻合，经过比较，3种算法下，将筛选出的重要特征变量作为预报因子，均可降低不重要变量对模型精度的干扰，从而提高模型模拟性能，因此，特征变量的筛选是训练始花期预报模型的基础和提升预报模型精度的有效方法，这与刘峻明等[33]、岳继博等[34]的研究结论一致。RF和BP两种机器学习算法的模拟精度要高于MLR算法的模拟精度，因为预报因子和始花期之间的关系并不是简单的线性关系，而是存在较为复杂的非线性关系，所以MLR算法中入选的自变量个数普遍偏少，过少的自变量无法较好表征对始花期的影响。RF算法收敛规则遵循大数定律、泛化误差具有收敛性，训练速度快，且不易产生过拟合；BP算法采用梯度下降的原理，收敛速度慢，易陷入局部极值点，导致神经网络的分类精度下降，所以RF算法下的建模速度要快于BP算法，且精度更高，但对于始花期极端年份的模拟过于“保守”，而BP算法则存在始花期波动幅度模拟过大的问题。RF算法中的树节点个数Mtry、BP算法中的神经节点个数Net是这两种机器学习算法中的重要参数，两种算法在训练模型时均是采取了随机抽样的方法，每次建立的模型精度存在差异，RF算法下训练样本的模拟精度均很高，BP算法下训练样本的模拟精度则不稳定，选取每个节点数对应的最优模型，对其预报结果集成能有效提高模型精度、减小随机误差。由于冬小麦始花期不仅与气象因子、播种期有关，实际还与田间管理、肥料的施用、作物品种等因素有关，因此，机器学习算法下的预报结果仍然存在一定的偏差，在实际应用时还需要结合田间实际情况。

综合而言，文中利用机器学习算法建立始花期预报模型的思路为预报冬小麦始花期提供了新的方法和思路，而且对 RF、BP、MLR三种算法的模拟精度的对比分析结果，可为选用更合理的预报模型提供依据。RF机器学习算法可在冬小麦始花期预测中进行应用，建立的预报模型较BP和MLR算法更具可靠性和准确性。预报结果可为农业部门抓住用药最佳时机提供指导，增强防治效果，保障小麦质量安全，减少盲目用药，减轻农药面源污染。

4 结 论

本文以冬小麦始花期为研究对象，利用随机森林机器学习算法，以精度平均减少值为评价指标，结合冬小麦生育期生长发育特点，筛选出对始花期影响较为重要的因子，分别利用随机森林算法和反向传播神经网络算法，随机选取训练样本和测试样本，经过成百上千次的学习，建立最优预测模型，并进行模型模拟精度的验证；同时还利用多元线性回归算法进行建模，比较了 3种算法下模型的模拟精度，得到以下主要结论：

1）冬小麦始花期存在较为明显的年际波动，大部分地区有提前趋势，各地冬小麦始花期历史最迟与最早相差天数都在21 d以上，不同区域间始花期存在差异。

2）随机森林算法重要性度量表明，温度类因子对始花期影响的重要性明显大于降水类和日照类，重要性排在前5位的因子是：上年12月－当年3月日均温≥0 ℃活动积温、上年 12月-当年 3月平均气温、上年 12月-当年3月最低气温≤0 ℃的累计日数、当年3月平均气温、上年12月-当年2月日均温≥0 ℃的活动积温。

3）3种算法建立的始花期预报模型，均可在4月初对冬小麦始花期进行预报，按照历史上始花期的极端年份，则最迟可以提前5 d预报，最早可以提前32 d预报。RF算法模拟精度最高，BP算法次之，MLR算法相对低一些。