结晶器凝固参数的正交分析*

杜风娇 刘建刚，2

(1武夷学院机电工程学院 福建南平 354300；2浙江理工大学机械与自动控制学院 浙江杭州 310018)

1研究背景

连铸坯钢与传统的模铸钢进行比较优点明显，如结晶器的振动技术在整个拉坯生产过程中，保护渣在坯壳与结晶器之间起到有效的“润滑”作用。结晶器振动能够使铸坯顺利的脱模，并且防止在钢坯在生产过程中其铸坯的表面和结晶器的内壁面发生粘结，及铸坯拉裂导致漏钢等严重现象的发生，研究负滑脱时间有利于钢坯连铸脱模。

王伟[1]采用Fluent数值模拟软件，对断面为180mm×610mm板坯连铸结晶器浸入式水口底部结构、浸入深度和拉速等工艺参数进行了优化研究，并对数值模拟结果进行了冷态水模拟验证。邹涛等[2]采用1∶2.2水模型试验与数值模拟对结晶器浸入式水口结构的改进与优化进行探究。通过不同铸坯断面下C型水口与A型水口对结晶器流场影响效果进行比较，得出水模试验与数模试验结果一致。谢集祥[3]对涟钢185 0mm×230mm板坯连铸结晶器流场和温度场进行了系统的数值模拟，研究了不同吹氩量(0～7 L/min)、不同水口浸入深度(110～150mm)和不同拉速(0.9～1.2m/min)对结晶器内钢液行为的综合影响，结果表明，随着吹氩量增加，自由液面的钢液流速和温度总体呈现降低的趋势；随着水口浸入深度增加，自由液面的钢液流速先降低后增加；随着拉速增加，自由液面的钢液流速增加；水口浸入深度和拉速对温度场的影响较小。薛瑞[4]采用Fluent软件对断面为160mm×160mm小方坯结晶器建立了三维稳态数学模型，模拟研究了160mm×160mm小方坯结晶器在不同拉速条件下相适应的水口浸入深度，并对数值模拟结果相应地进行了水模拟验证。朱苗勇[5]提出新一代高效连铸机应具有克服这些缺陷的固有特性，结晶器、二冷区和凝固末端等3个冷却区的新技术开发及应用代表了其发展方向，应成为连铸机升级发展的标配技术，根本上解决连铸生产过程频发的裂纹、偏析及疏松等凝固缺陷是制约其高效化发展的瓶颈。综上所述，目前国内研究者对结晶器内多种参数做了一定研究与优化，但是都是研究结晶器水口处的形状等参数。基于此，文章采用正交设计的方法探讨结晶器振动参数(振动振幅、振动频率、拉皮速度)对方坯连铸机结晶器内凝固工艺参数(负滑脱时间、液态渣膜消耗量、钢坯振痕深度)变化关系，利用Fluent软件对正交优化设计后的结晶器内钢水凝固进行仿真。

结晶器的振动规律有：梯形速度、矩形速度、非正弦速度、正弦速度。文章采用正弦振动方式，即采用四连杆机构的半板簧振动机构如图1所示。该振动机构工作原理为：将板簧取代四连杆机构当中的连杆，实现结晶器的振动轨迹为近似的圆弧轨迹，用板簧代替连杆还可以减少使用轴承的个数及降低因轴承使用时的间隙所带来的运动误差，从而将进一步提高结晶器振动的轨迹精度。

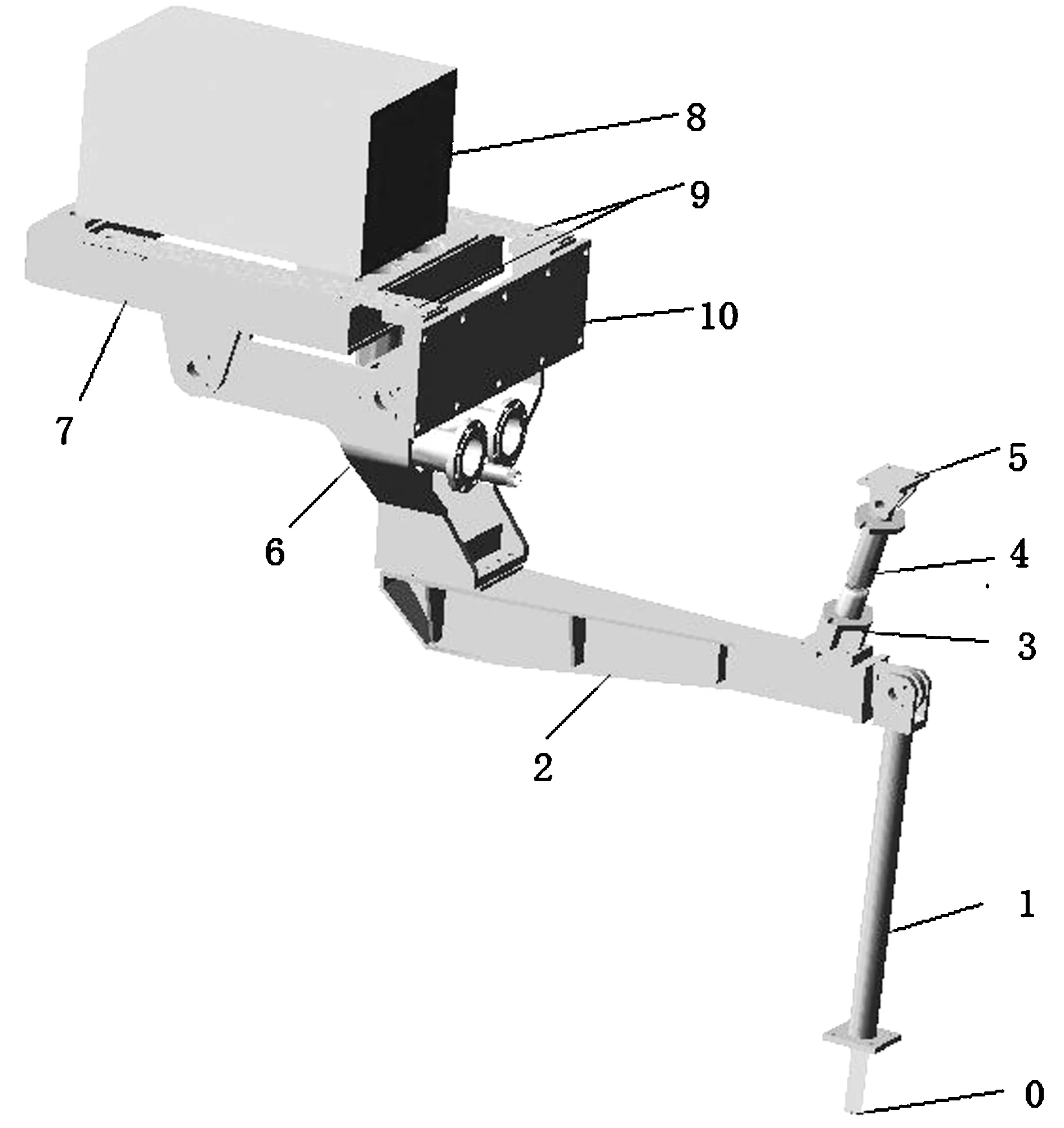
0-曲柄偏心轴，1-连杆，2-传动臂，3-下支座，4-弹簧座，5-上支座，6-摆动臂，7-振动台，8-结晶器，9-支座，10-支座

2结晶器凝固工艺参数的理论分析

结晶器内钢水的凝固是一个非常复杂的多相流问题，而负滑脱时间、液态渣膜的厚度、振痕深度直接影响铸坯的质量。而液态渣膜消耗量对振痕深度与液渣膜消耗量存在直接关联，且负滑脱时间与拉坯速度也存在匹配关系，所以液态渣膜厚度的计算、及负滑脱时间对钢水凝固的效果和铸坯质量至关重要，

2.1液态渣膜厚度的确定

液态渣膜厚度hx直接影响结晶器内摩擦力。液态渣膜厚度由结晶器内壁面的弯月面处的间隙的宽度和钢水凝固的收缩所形成的缝隙宽度所组成。

假设保护渣凝固温度低于已凝固固态铸坯表面温度，钢水凝固收缩缝隙宽度为所求的缝隙宽度(即为渣膜的总厚度)。为简化铸坯与结晶器内壁面之间缝隙，文章假设不考虑铸坯的其它固态相变过程，奥氏体是钢水在结晶器内唯一存在的金相模式，忽略凝固坯壳之间的力学作用。结晶器内因钢水凝固的收缩所形成的缝隙宽度等于液态渣膜的厚度[7]。

(1)

式(1)中：E—钢的线收缩系数0.0001，1/℃；θmould—结晶器倒锥度的0.8%；i—铸坯坯壳节点数；Ti—坯壳节点温度，℃；x—距弯月面的距离，mm；Ts—固相线温度，℃；i′—最后凝固节点数；L—结晶器宽度，mm。

由于钢水液面下弯月面附近的钢水为液态的形式，结晶器弯月面的间隙宽度，文章忽略钢水凝固收缩导致的铸坯与结晶器壁面之间的间隙，在此文章引用Bikerman提出的在弯月面处的钢水处于静态形状时的方程来计算结晶器内壁面的弯月面处的间隙的宽度[8]。

(2)

式(2)中：a—间隙宽度的计算时的虚拟参数；x—沿结晶器深度方向钢水距离结晶器上表面的距离。

(3)

式(3)中：σs-f—钢渣截面的张力，N/m；；g—重力加速度，m/s2ρslag—保护渣密度，kg/m3；ρsteel—固态钢密度，kg/m3。公式(3)简化为如公式(5)所示

(4)

式(4)中的间隙宽度中的参数取值：L1=7mm，d1=15mm，d2=0.2mm，由于距结晶器内的弯月面的距离7mm以下的dmeniscus基本趋近于零，因此铸坯和结晶器壁面之间的缝隙宽度的计算模型简化公式(6)所示计算。

hx=Gap+dmeniscus

(5)

由(1)、式(2)和式(5)可得结晶器的液态渣膜的厚度值。

2.2 等负滑动时间匹配控制模型

等负滑脱时间相匹配[9-10]控制模型如公式(6)所示。给定一个不变的负滑脱时间tn的值，可以计算与其匹配的拉坯速度。

(6)

图2为负滑脱时间为0.08 s、振幅为4mm工作条件下的拉坯速度与结晶器的振动频率之间的匹配关系图。由图2可知，对应拉坯速度随着振动频率的变大而变小。

图2 负滑脱时间为0.08 s，振幅为4mm时拉速与振动频率之间的匹配关系图

3负滑脱正交分析

利用正交试验对负滑脱进行正交设计分析。文章中3个因素都各取4个水平。3个因数分别是结晶器振动振幅和结晶器振动频率。振动频率取：175，195，215，235次/min；振幅取：2、3、3.5、4mm；拉坯速度取：1.4 、1.8 、2.0、3.0m/min。负滑脱时间的计算表达式[4]如下所示

(7)

式(7)中：vc—拉坯速度，m/min；f—振动频率，Hz；a—振幅，mm；tn-负滑脱时间。

钢铁大学(steeluniversity.org)是由国际钢铁协会发起成立的，是一个对钢铁厂的连铸连轧冶炼过程进行数值模拟网站，该网站可以进行钢铁连铸在线模拟分析，文章利用钢铁大学网站模拟正交设计中结晶器在不同振动参数和拉坯速度下的负滑脱时间，结果如表1所示。

表1 负滑脱时间的正交分析表

对正交结果数据进行方差分析可得：极差值(Range)的大小反应着变量对实验的结果的影响程度，又有F值=(因素的平均差方和(Average)/误差的平均差方和(DevSq))，Fratio=(F值/相应显著水平下的Fvalue)，Fvalue可以由F分布表[11，12]中查得。振动频率的Fratio：Fratio=0.462；振动振幅的Fratio：Fratio=1.154；拉坯速度的Fratio：Fratio=1.385。由极值结果可知：三个振动参数影响因数中对负滑脱时间影响力排序应该为vc、a、f；由Fratio值结果可知：vc、a对tn影响都显著；f对tn无明显影响。

由表1可知，在拉坯速度、振动频率同等条件下，负滑脱时间变化规律为：随结晶器的振动振幅增大而增大；在相同的振动频率、振动振幅同等情况下，负滑脱时间变化规律为随拉坯的速度增大而减小；

在拉坯速度、振幅同等条件下，负滑脱时间变化规律为随振动频率的增大而增大。

不同的振动频率下，给定tn值后，可以得出振幅与拉坯速度之间的关系。利用Matlab软件绘制负滑脱时间的等值线图(不同振动频率的的负滑脱时间等值线图)如图3-图6所示。根据图片后处理Datatip工具在图3-图6的负滑脱等值线图上标注关键点的对应的坐标取值。

图3 负滑脱时间等值线图(振动频率为175次/min)

图4 负滑脱时间等值线图(振动频率为195次/min)

图5 负滑脱时间等值线图(振动频率为215次/min)

图6 负滑脱时间等值线图(振动频率为235次/min)

由图3-图6可知，结晶器振动时连铸坯的负滑脱时间的变化规律如下：在相同的拉坯速度及相同的振动频率情况下时，其负滑脱时间随着振动振幅变大而变大；在相同的振动振幅及相同拉坯速度的情况下时，其负滑脱时间随着振动频率的增大而增大；在相同的振动频率及相同的振动振幅情况下时，其负滑脱时间随拉坯的速度增大而减少。

4铸坯振痕深度

影响铸坯表面质量因素复杂多变，铸坯振痕深度和振痕宽度是铸坯产品的表面质量的重要决定因素，针对不同振动参数下的振痕深度。振痕深度的计算模型[13]如式(8)所示。

L=3.14×cos(1.8β)×S

(8)

式中：L—振痕间距，mm；S—振程(振幅的两倍)，m；β—负滑脱率%；同理可得，利用钢铁大学网站数值模拟功能针对结晶器不同振动参数的液渣膜消耗量及振痕深度进行仿真，振痕深度计算结果如表2所示。

表2 振痕深度正交表

对正交的结果进行方差研究分析可得：振动频率的Fratio：Fratio=0.054；振动振幅的Fratio：Fratio=2.732；拉坯速度的Fratio：Fratio=0.214，由极值结果可知：影响的变量因数中对振痕深度影响力排序应该为a、vc、f；由Fratio值结果可知：a对振痕深度影响非常显著，vc、f对振痕深度影响不明显。

利用Matlab软件绘制振痕深度等值线图，振痕深度的等值线图如图7-图10所示(图中level的值为振痕深度值)。

图7 频率175次/min振痕深度等值线图

图8 频率195次/min振痕深度等值线图

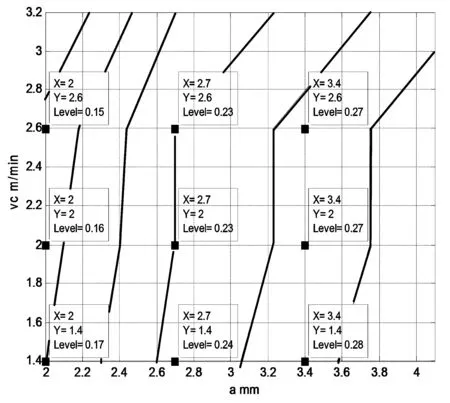
图9 频率215次/min振痕深度等值线图

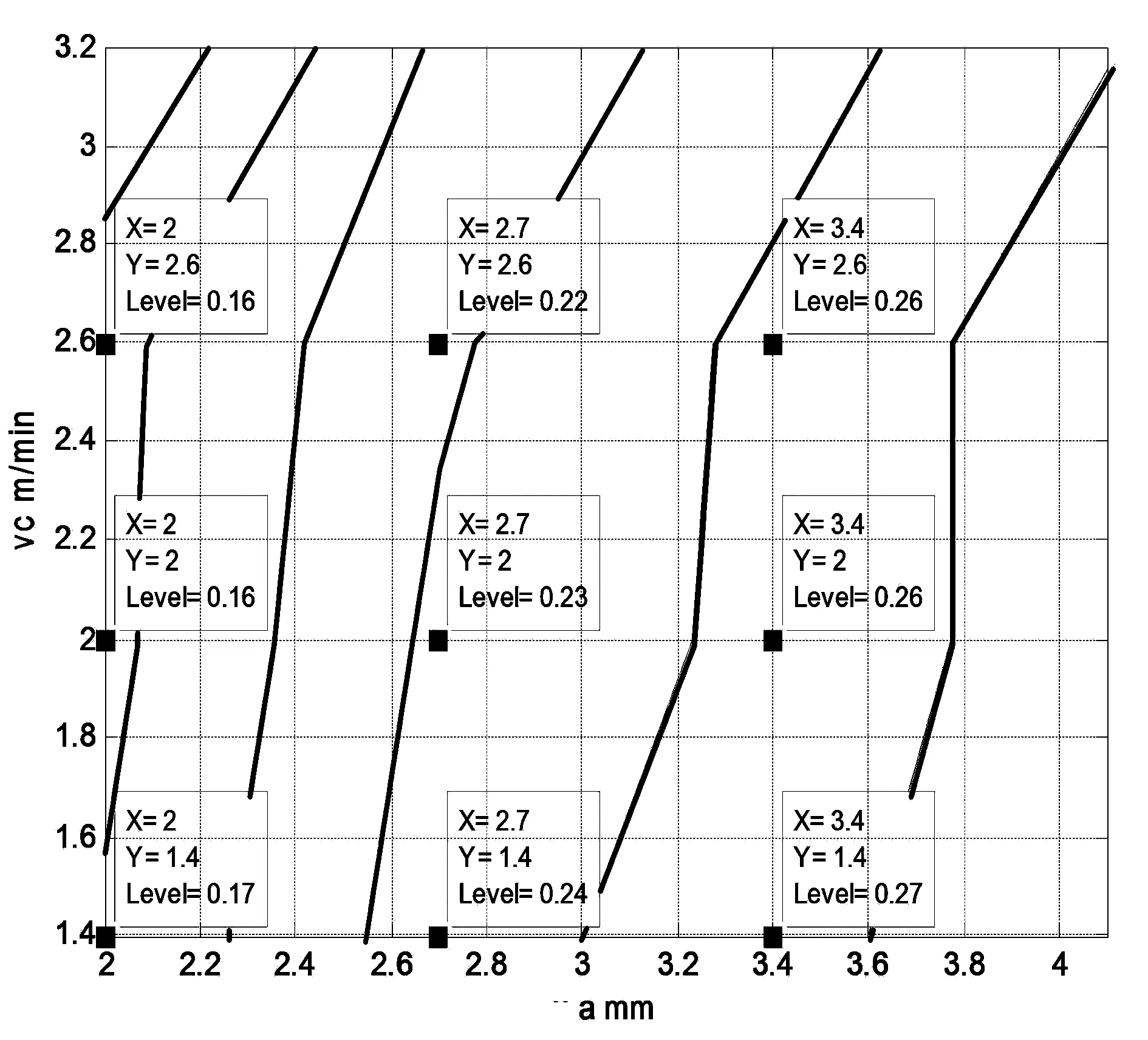
图10 频率235次/min振痕深度等值线图

根据图7-图10的走势形状可知，结晶器振动频率的改变对结晶器内的保护渣消耗量影响关系不明显。根据图7-图10的振痕深度的等值线的纵、横坐标比值可知，拉坯速度增大，铸坯表面的凝固效率减少，表面振痕深度变浅，振幅通过对铸坯的割伤程度影响和改变振痕深度，振痕深度越大，满足同等振痕深度前提下，可调整结晶器的振幅和拉速之间的关系，振痕深度随振动振幅变化非常敏感。

5液渣膜消耗量

振痕深度与保护渣的消耗量存在关联，保护渣的消耗量计算模型[14-15]如式(9)所示。

(9)

式中：Q—保护渣的消耗量，kg/m2；vc—拉坯速度m/s；f—频率，min-1。液渣膜消耗量的多少对钢坯的润滑情况影响敏感，随液态渣膜消耗量的增大润滑越改效果越明显，但过多消耗必液渣膜将对钢坯纯度带来负面的影响，钢坯的杂志过多会改变钢坯的力学性能，液渣膜消耗量随拉坯速度及振幅、频率的正交情况如表3所示。

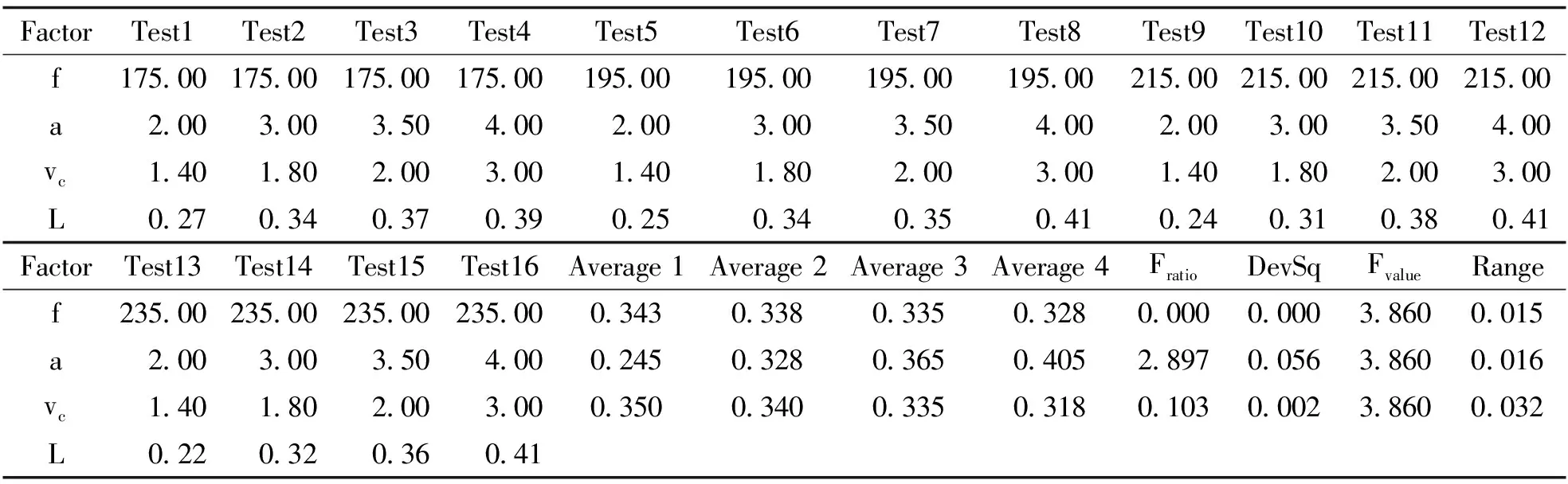
表3 保护渣消耗量正交设计表

对保护渣消耗量正交结果进行方差研究分析可得：振动频率的Fratio：Fratio=0；振动振幅的Fratio：Fratio=2.897；拉坯速度的Fratio：Fratio=0.103；由极值结果可知：影响因数对振痕深度影响力排序应该为a、vc、f；由Fratio值结果可知：a对Q有显著性非常明显，看不出vc对Q显著性的影响。f对Q没有任何显著性。

利用Matlab软件绘制结晶器内钢水的液态保护渣消耗量的等值线图，不同振动频率，保护渣消耗量的等值线图如图11-图14所示(图中level的值为保护渣消耗量值)。

图11 频率175次/min保护渣消耗量等值线图

图12 频率195次/min保护渣消耗量等值线图

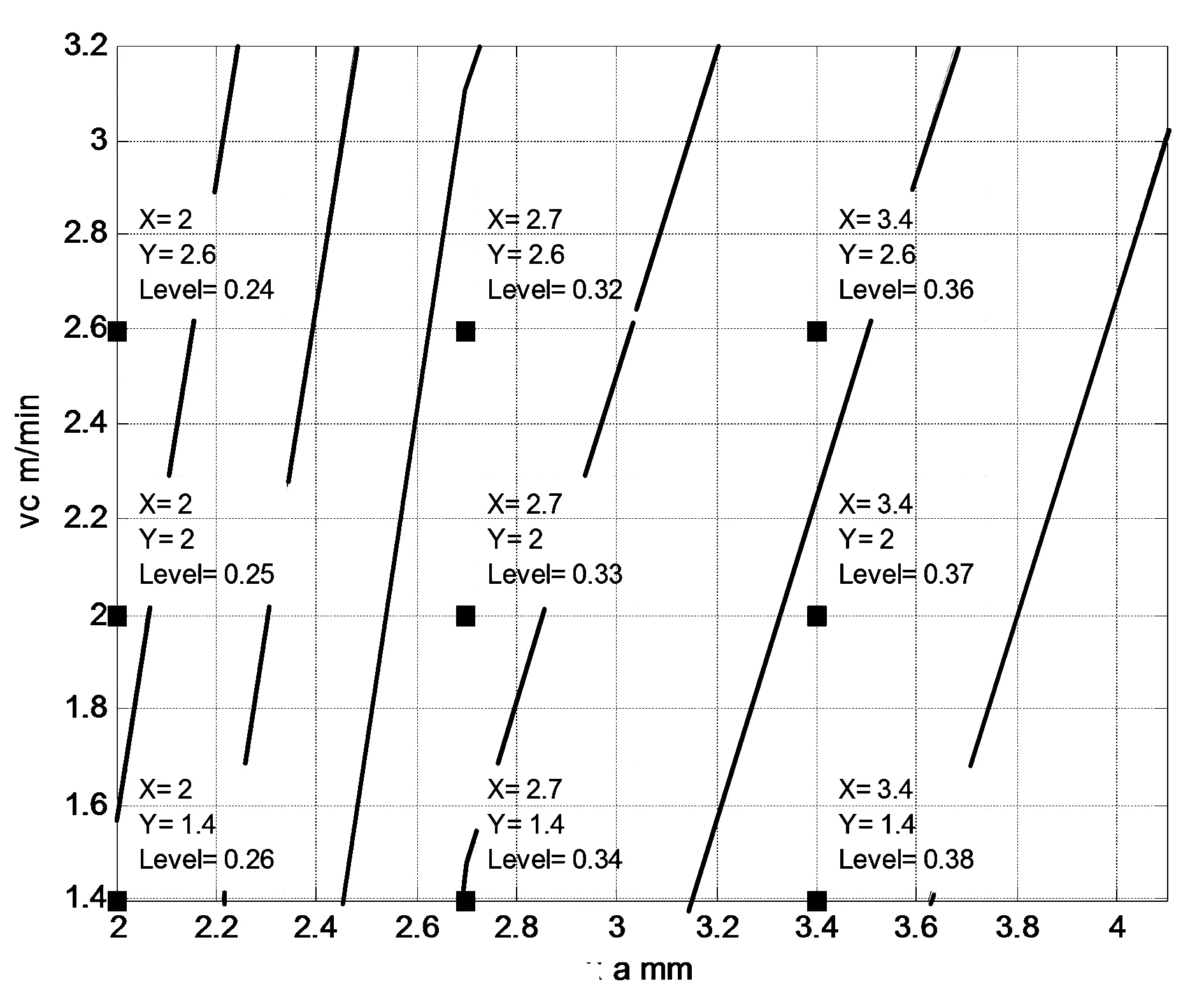
图13 频率215次/min保护渣消耗量等值线图

图14 频率235次/min保护渣消耗量等值线图

由图11-图14可知，保护渣的消耗量受结晶器振动频率的影响不明显，保护渣消耗量的等值线斜率变化关系可知，拉坯速度对结晶器内保护渣的消耗量影响非常敏感，可通过调整拉坯速度和振动振幅的匹配关系来保证保护渣的消耗量。

由以上结晶器振动装置振动参数(振动振幅、振动频率、拉皮速度)对结晶器内钢水的凝固工艺参数(负滑脱时间、液态渣膜消耗量、钢坯振痕深度)的变化关系，基于专家经验，得出正交优化最佳匹配的结晶器振动参数为：振动频率f=175次/min，振幅a=1.8mm，拉坯速度vc=2.4m/min。对应结晶器凝固工艺参数为：负滑脱时间tn=0.0361s，保护渣消耗量Q=0.2277kg.m^2，振痕深度h=0.113mm。

6基于Fluent软件结晶器内钢水仿真

利用Fluent软件对正交设计优化后参数进行凝固模拟仿真，观察和验证此振动参数下钢水的凝固、结晶器钢水的入口处的速度、结晶器内钢水的运动轨迹、结晶器内钢水的流场等情况以及温度场的变化关系，钢水物性参数及结晶器振动参数设置如下所示：方坯边长160mm；钢水的动力黏度0.006 Pa·s；总钢坯模拟长度960mm；液相线温度179 3.5℃；有效结晶器长度900mm；潜热272 220 J·kg-1；水口浸入式深度40mm；固相线温度176 3.5℃；钢水的浇铸温度181 3.5℃；拉坯速度0.988m·min-1；比热容690 J·(kg·℃)-1；，振动振幅0.0012m，振动频率216(Hz)，仿真结果如图15-图20所示。

图15 结晶器内钢水中间截面液相系数分布图

图16 结晶器内钢水中间截面入口处速度图(放大10倍)

图17 Y轴截面钢水温度分布图(℃)

图18 钢水等温线图(℃)

图20 结晶器内沿y方向(x=z=0)截面颗粒的轨迹

利用后处理Tecplot软件进行处理后，得出结晶器内钢水的等温线图如图18示。由图18可知，结晶器内浸入水口的温度变化不大，结晶器的周边温度≤1763.5 ℃，已经达到钢水的凝固点，说明结晶器内壁面的钢水已经凝固成固态的钢坯金相组织。

由图18和图19可知结晶器内中心温度最高，越靠近结晶器外表壁面温度呈现降低的关系，由图15结晶器内凝固的液相系数图可知，结晶器内钢水靠近壁面部分已经达到钢水的凝固状态，而结晶器的中心钢水还以液态状态呈现，通过对比可知，钢水已经为固态的、凝固的单边厚度有明显的改善；由图16可知，结晶器入口处速度靠近浸入水口附近有两个漩涡，此处的漩涡方便液态渣膜漂浮到钢水表面上，减少了钢水中的杂质含量。由图20可知，钢水在结晶器内的运动轨迹良好。

由图21和图22可知，结晶器中心处的轴向速度分布最大，而越靠近结晶器周边，速度分布越小。这样结晶器内钢水的流动速度关于结晶器的垂直方向就会出现一个梯度。

图21 结晶器垂直y轴任意截面y向速度关于z轴的速度分布图

图22 结晶器垂直y轴任意截面y向速度关于z轴液相系数分布图

7结论

文章对结晶器内凝固参数进行了正交分析，以振动频率、振动振幅、拉坯速度为正交设计变量。利用钢铁大学(steeluniversity.org)网站分别仿真不同正交参数下结晶器内负滑脱时间、振痕深度、保护渣消耗量变化关系。根据结晶器内负滑脱时间、振痕深度、保护渣消耗量随振动频率、振动振幅、拉坯速度变化关系，确定一组最优的振动频率、振动振幅、拉坯速度参数组合。利用Fluen对最优参数组合进行模拟仿真，得出结晶器内钢水的凝固状况：液相系数、温度场分布、颗粒的轨迹、结晶器入口处速度分布、结晶器内钢水的速度分布图。根据Fluent仿真结果验真正交优化设计的准确性、合理性。