基于姿态角信息的载体升沉位移测量

李 鹏，魏宗康，石 阳，李海兵，3，罗 骋，3

(1.北京航天控制仪器研究所，北京 100039；2.火箭军装备部驻北京地区第四军事代表室，北京 100039；3.青岛海洋科学与技术试点国家实验室，青岛 266237)

0 引言

水面舰船或水下潜航器开展作业任务时往往受海浪波动的影响，会产生升沉及摇摆运动。水面舰船及作业平台的升沉对其作业任务存在较大的影响[1-4]，需要实时测量升沉信息，进行升沉补偿。由于水下潜航器无法通过GPS进行水下导航定位，因此一般使用深度计修正高度通道。但是，由于水下环境复杂多变，高度通道失去外部测量信息后无法获取精确信息，直接影响了水下潜航器的定位精度。因此，对水面及水下载体的升沉信息进行精确测量具有重要的现实意义。

载体的升沉运动不仅包含天向的位移运动，还包含了横摇、纵摇及艏摇等姿态变化。升沉位移可以通过天向的加速度信息经过两次积分获得，但是惯性导航系统在高度通道发散，因此需要对高度通道的信息进行滤波，将Schuler周期、Foucault周期及其他低频噪声进行滤除，从而得到精确的升沉位移。传统的测量方式可使用外部参考信息进行组合定位，但是面对复杂的水面和水下环境，定位的精度和实时性不高。另一种测量方式可通过高通滤波器实现精确的升沉位移测量，但是存在较大的滞后性。文献[5]引入了加权Fourier组合算法(WFLC)对IIR高通滤波器的超前特性进行校正，从而实现了对线运动信息的精确测量。文献[6]提出了一种基于NARX神经网络的船舶升沉运动实时预测方法，在复杂海浪环境中具有良好的适应性。文献[7]提出了一种互补性无延时高通滤波器设计方法，该方法解决了信号的延时问题，为工程作业提供了一种切实可行的方式。文献[8]在此基础上提出了自适应滤波方法，使得滤波效果更贴近实际情况，但是没有对海浪波动特性的提取途径及适用性进行详细说明。由于载体的姿态变化与海浪波动频率相近[9]，因此本文提出通过三个姿态角信息提取海浪波动频率，进行加权处理，获得滤波器截至频率，通过窗口滑动提取频率实现自适应滤波，最后通过实测海试数据进行验证，结果显示测量误差为厘米级，证明该方法切实有效。

1 载体升沉位移测量原理

一般情况下，水面舰船及水下潜航器均配有惯性导航系统，而姿态角、升沉加速度信息可由惯导系统获得。首先根据姿态信息获得海浪波动特性，实现自适应滤波器设计，接着对升沉加速度进行滤波-积分，获得升沉方向的速度信息，然后再进行滤波-积分，获得升沉方向的位移信息，最后再进行滤波，最终获得精确的升沉位移信息。载体的升沉位移测量原理如图1所示。

图1 升沉位移测量原理Fig.1 Principle of heave displacement measurement

2 海浪波动特性提取

2.1 姿态角获取

本文通过对载体姿态角信息进行分析，来提取海浪波动特性。姿态信息的精度与初始对准精度紧密相关，本文以动基座初始对准为例，说明姿态角测量及姿态角与海浪波动特性的关系，为滤波器设计提供依据。

不论水面舰船还是水下潜航器，初始对准阶段均可在水面上进行，通过GPS获取位置经纬度等初始信息。为了实现动基座下的快速精对准，本文通过H∞控制理论[10]分别对水平通道和方位通道进行控制器设计，实现姿态信息的快速精对准。东向姿态通道和北向姿态通道的控制回路如图2、图3所示。

图2 东向姿态对准回路Fig.2 Diagram of east orientation attitude alignment loop

图3 北向姿态对准回路Fig.3 Diagram of north orientation attitude alignment loop

由于两个方向的姿态控制回路相近，故可使用同一个控制器。经过对性能界函数参数选取，得到水平方向对准回路的控制器如式(2)所示，其开环传递函数Bode图如图4所示。

图4 水平通道控制回路开环传递函数Bode图Fig.4 Bode plot of open loop transfer function of horizontalchannelcontrolloop

由控制器可知，水平通道的开环截止频率为50rad／s，虽然系统带宽较大，但是在保证姿态精度的前提下还原了载体的运动状态。经过海试试验，水平通道的精对准结果如图5所示。由图5可知，水平通道未发散，Schuler周期等低频成分均被控制器阻尼掉了。

在初始对准过程中，捷联惯导系统一般先进行水平对准，待水平对准稳定后，再进行方位对准。考虑到性能界函数，方位对准回路的方框图如图6所示。

通过设置性能界函数，使得方位对准回路的控制器如式(3)所示，对应的开环传递函数Bode图如图7所示。在水平对准100s后进行方位对准，对准结果如图8所示。

图5 水平通道精对准结果Fig.5 Fine alignment results of horizontal channel

图6 方位对准回路Fig.6 Diagram of azimuth alignment loop

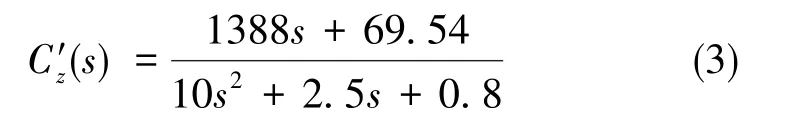
图7 方位通道控制回路开环传递函数Bode图Fig.7 Bode plot of open loop transfer function of azimuth channel control loop

图8 方位角精对准结果Fig.8 Fine alignment result of azimuth angle

2.2 海浪波动特性提取及分析

海浪的波动使得载体产生横摇、纵摇以及艏摇，同时波浪的起伏使得载体产生同周期的升沉运动，波浪的幅值即为载体的升沉位移，因此载体的姿态信息里包含了海浪的波动特性。海浪的波动可以看作由无限个振幅、频率、初始相位不等的简谐波叠加而成，这些简谐波便构成了海浪谱，通过分析载体姿态角的频谱特性，便可提取引起载体运动的海浪谱信息，三个姿态角的频谱特性如图9～图11所示。

图9 滚动角功率谱密度Fig.9 Power spectral density of rolling angle

图10 俯仰角功率谱密度Fig.10 Power spectraldensity of pitch angle

图11 方位角功率谱密度Fig.11 Power spectraldensity of azimuth angle

由姿态角的谱密度曲线可以看出，三个方向的姿态角含有多个谐振峰，各姿态角的主要频谱特性如表1所示。

由表1可知，姿态角的频谱特性较为一致，在0.05Hz、0.12Hz、0.22Hz、0.46Hz、12.42Hz附近高度重叠，其对应的峰值正好反映了姿态变化中的噪声水平。其中，12.42Hz处的峰值非常低，对载体运动的影响可忽略不计，由此可确定载体所处的环境特征，进而通过设计滤波器实现载体升沉的精确测量。

表1姿态角频谱分析Table1 Spectrum analysis of attitude angle

3 自适应滤波器设计

相较其他典型滤波器，Butterworth滤波器的频率响应曲线在通频带内具有最大的平坦度，没有起伏，在阻频带则逐渐下降为零，该滤波器适用于包含低频成分的信号随时间累计积分而缓慢发散的滤波问题。传统的滤波器则直接采用高通滤波形式滤除低频成分，但这种高通滤波方式会带来不小的时延问题。互补型高通滤波器的主要设计思想是以Butterworth滤波器为基础，先设计低通滤波器，那么经过滤波的信号可表示为

式(4)中，yl(z)为滤波后的低频信号，Hl(z)为低通滤波器，x(z)为输入信号。为了滤除低频成分，可以利用下式反向求取高频信号yh(z)。

式(5)可转换为

式(6)中，Hh(z)＝1－Hl(z)，Hh(z)即为所要设计的高通滤波器。当滤波器的阻带衰减足够大时，对高频信号的滤除能力就越强。根据互补性可知，经过反向处理后，Hh(z)可让高频信号顺畅通过，并且延时也会小到可忽略不计。

在自适应滤波器的设计中，需要对滤波器参数进行设置，包括通带截止频率fp、阻带截止频率fs、通带衰减Ap和阻带衰减As。其中，Ap和As选取较为容易，重点是如何实现fp和fs的设置。根据姿态角频率特性分析结果，载体主要受到频点约为0.05Hz、0.12Hz、0.22Hz和0.46Hz的海浪谱影响。本文将各姿态角最小谐振频率对应的谱密度峰值按照式(7)进行归一化处理，可以得到通带截止频率的影响因子，进而按照式(8)计算fp。

式(7)中，Aep、Anp、Aup分别为各姿态角的第一个谐振主峰的幅值，即表1序号1一行中滚动角、俯仰角和方位角对应的峰值；Kep、Knp、Kup分别为滚动角、俯仰角和方位角的通带截止频率影响因子。

式(8)中，fep、fnp、fup分别为滚动角、俯仰角和方位角的第一个谐振主峰对应的谐振频点，即表1序号1一行中滚动角、俯仰角和方位角对应的频率。

同理，根据表1序号4一行中各姿态角对应的频率和峰值，即最后一个主峰对应的频点和幅值，可以计算出滚动角、俯仰角和方位角的阻带截止频率影响因子和阻带截止频率。根据上述方法，可得到fp＝0.058996Hz、fs＝0.4663Hz。

根据上述确定的滤波参数，按照式(9)对低通Butterworth滤波器的滤波阶数N和截止频率ωc进行计算，最后可得到相应的低通滤波器Hl(z)以及互补后的高通滤波器Hh(z)。

式(9)中，f为系统的采样频率。那么在载体升沉周期内的某个固定时间窗口期内，按照上述方法，通过姿态角信息进行海浪波动特性提取，即可实现自适应的滤波器参数设置，进而实现自适应滤波。

4 海试验证

随机截取某次海试试验部分数据进行验证。其中，图12(a)为滤波前的升沉速度和升沉位移。可以看出，升沉速度及升沉位移随时间而发散，不能体现载体实际的升沉信息变化。

通过对截取的数据进行分析，得到的低通滤波器如下所示

滤波器互补后，其高通滤波器如下

经过滤波计算，升沉信息如图12(b)所示。可以看出，载体的升沉高度变化约为0.05m，高度通道的发散被有效地阻尼掉了。对升沉信息进行谱分析，结果如图13所示。可见，升沉信息的谐振频率与姿态信息中的谐振频率一致，而小于截止频率的信息得到了有效抑制。

图12 升沉信息提取前后的对比Fig.12 Comparison of heave information before and after extraction

图13 升沉信息的功率谱密度Fig.13 Power spectraldensity of heave information

图14 升沉运动试验结果比对Fig.14 Comparison of heave motion test results

本文使用Matlab中的零相位滤波器函数filtfilt对样本数据进行升沉信息提取，用于升沉位移比对基准，图14为船体在700s～900s的数据比对情况。其中，升沉速度信息几乎重合，升沉位移信息与基准信息重合度高。由对比曲线可知，该自适应滤波器的延时很小，可忽略不计。取全部滤波数据与基准数据进行比对，其最大误差为1.6cm，升沉位移的均方根为0.42cm。同样以filtfilt的滤波结果作为基准数据，比对固定频率参数的滤波器处理结果，其最大误差为3.4cm，升沉位移的均方根为1.29cm。

5 结论

对舰船及水下航行器因海浪而产生的升沉位移进行精确测量，可有效保证航行中载体执行任务的可靠性，具有重要的现实意义。本文首先通过惯导系统获得精确的姿态角，提出了自适应滤波器，该滤波器从固定周期内的姿态信息中提取海浪波动特性，然后通过影响因子分配各滤波频率的权重。此外，该滤波器采用互补方式，具有超低延时的特点。通过该滤波器，最终获得低延时、高精度的载体升沉位移。本文通过海试数据，以精对准过程作为海浪波动特性获取来源，进行自适应滤波。通过Matlab中的filtfilt函数进行事后的无延时滤波处理，并将处理结果作为基准数据。通过比对分析，证明本文提出的自适应滤波器设计方法可行、有效，相位误差可忽略不计，测量误差为厘米级，均方根精度显示该滤波方式更优越。