多源融合导航系统的因子图算法综述
罗子岩,陈 帅,王国栋,赵海飞,马永犇
(1.南京理工大学自动化学院,南京 210094;2.北京航天控制仪器研究所,北京 100039)
0 引言
导航定位技术是现代战争中不可或缺的关键技术,在精确打击和协同作战中发挥着重要作用,同时也在无人驾驶等民用领域广泛应用。目前,随着对导航定位性能的要求越来越高以及导航环境的日益恶劣,集成在一起的传感器种类和数量也不断增加,导航手段已从单一导航方法发展到多源、全源组合导航系统阶段,多传感器的组合导航系统已经逐渐成为各种复杂环境下长时间高精度导航的主要方式。
在多传感器数据融合方面,目前采用较多的方法是联邦Kalman滤波算法。但是,多传感器数据融合系统往往各个传感器的频率不同,误差特性也不同,传统的Kalman滤波算法为了保持数据的同步往往需要丢弃一部分测量值,这样会造成信息的浪费。同时,标准Kalman滤波器只能解决线性问题,而大多数传感器模型都包含了非线性成分。扩展Kalman滤波算法应用于非线性状态估计系统中虽然已经得到了学术界认可并被广泛使用,然而该种方法也带来了两个缺点:1)当强非线性时其违背局部线性假设,Taylor展开式中被忽略的高阶项带来大的误差时,扩展Kalman滤波算法可能会使滤波发散;2)由于在线性化处理时需要用Jacobi矩阵,其繁琐的计算过程导致该方法实现相对困难。
然而在因子图框架下,每个传感器的测量值被编码成为一个因子,只需在产生测量值时加入组成框架图,通过对这些连接起来的因子使用Bayes推理来完成数据融合和参数估计。这种方法显然适用于处理异质异构非周期数据融合问题,具有很高的灵活性,能够以即插即用的方式配置、组合传感器,如果有传感器失效,也可以从因子图框架中及时删除。因此在多源组合导航中,因子图的身影出现得越来越频繁,其在无人机、自主水下潜器(Autonomous Underwater Vehicle,AUV)、无人驾驶等领域都有相应的应用,并且逐渐出现了各种基于因子图的改进算法[1]。本文将对因子图模型理论以及因子图算法的应用情况进行研究,并展望其发展前景。
1 因子图模型
将一个具有多变量的全局函数因子分解,得到几个局部函数的乘积,以此为基础得到的一个双向图叫做因子图。因子图是概率图模型的一种,其不仅可以被用来解决数学概率问题,还能被用来解决人工智能、信号处理、数字通信等其他领域的复杂问题[2]。当处理包含许多变量的全局函数时,通常采用的方法是利用给定函数的因子作为一个局部函数,然后由许多个局部函数的乘积表示全局函数。因子图便是表示这样的因式分解的二分图模型[3],因子图模型由变量节点、因子节点以及联系两者的边组成。若包含多变量的全局函数g(x1,x2,…,xn)可被分解为局部函数的乘积,则有

式(1)的因式分解可以使用因子图表示,且在此双向图中,xn表示为一个变形节点,局部函数fj表示为因子节点,Xj表示第j个局部函数fj(·)的自变量点集,再由表示相互关系的边将因子节点与相应的变量节点联系起来,下面给出一个具体的例子。
设g(x1,x2,x3,x4,x5)为一个包含五个变量的全局函数,同时该函数还可以被表示为:g(x1,x2,x3,x4,x5) =fA(x1,x2)fB(x2,x3,x4)fC(x4,x5), 则其对应的因子图如图1所示。

图1 因子图结构示意图Fig.1 Structure diagram of factor graph


导航系统中,量测函数通常可以根据状态变量估计预测出传感器的量测值。而因子节点计算预测的测量值和实际测量值之间的差值通过构建相应函数获得状态变量估计,因子节点获取预测的量测信息和实际量测信息的差值构建相应的指标函数从而获取代价函数,即

式(3)中,hi(Xi)为与状态变量有关的量测函数,zi为由传感器得到的实际测量值,L(·)为代价函数。对于Gauss噪声分布,L(·)为平方马氏距离,定义为L(e)=eT∑-1e,∑通常取量测噪声方差阵R[4]。
2 基于因子图的多传感器信息融合实现
2.1 卫星惯性组合导航实现与因子图算法可行性分析
文献[5]以发射惯性系为导航坐标系,选取SINS基本误差和惯性器件误差参数构成15维系统状态向量,在全软化仿真平台系统中通过轨迹发生器和卫星信号模拟器依次模拟生成导弹的惯组数据和GPS中频信号,再对生成的角速率和比力数据进行惯导解算,将GPS中频信号注入软件接收机进行导航解算,建立发射惯性坐标系下惯性/卫星松组合导航状态方程,采用传统的Kalman滤波算法和因子图算法进行信息融合。实验显示,运用因子图融合算法的三轴位置均方误差绝对值均比传统Kalman滤波算法的误差略小,较传统滤波结果有一定的改善。结果表明,因子图算法可以保证导航系统的正常使用且导航精度可以得到保障。文献[6]则以惯性卫星紧组合导航为背景对因子图算法代替Kalman滤波的可行性进行了研究,假设每个卫星就是一个传感器,提供一组量测信息,同时通过因子图来表示状态的递推与更新。通过Gauss-Newton迭代法求解优化方程,得到最优的状态修正量,实验结果同样证明了因子图算法的有效性。
2.2 因子图算法国外研究现状
2012年,美国Georgia理工学院的Indelman等针对美国国防高级研究计划局(DARPA)提出的全源定位导航项目并参照Dellaert等的一些平滑定位算法提出了基于因子图框架的多源导航传感器融合算法[7-8]。2013年,美国SRI国际公司的Chiu等[1]在美国Georgia理工学院研究的基础上针对机器人自主导航问题给出了基于因子图的组合导航系统,该系统包含了57种不同的传感器。其后,德国Chemnitz工业大学的Lange等[6]将基于因子图框架的增量平滑多源导航传感器融合方法应用到装配有惯性测量单元、光流传感器和无限反高度表的四旋翼无人机中,并与传统的扩展Kalman滤波方法进行对比,仿真实验结果验证了基于因子图的增量平滑算法相比传统滤波算法的优势。
目前来说,国外的学者对基于因子图框架的多源数据融合方法已经进行了深入的研究,并且可以较好地处理异步、多速率数据。但是,研究的应用背景多以小场景多动态SLAM问题为主,尚未在实地大场景下进行验证。
2.3 因子图算法应用
组合导航系统面临无人机、导弹、水下潜器等多种使用场景,以及卫星信号被干扰、不同传感器的使用等各种特殊的情况。因此,因子图算法被应用于多种使用场景并衍生出基于因子图算法的各种改进算法。
没有就算了。村长适时接过话头。八斗丘补偿问题,村委过些天会研究,你不要到处找人说事。特别是不要找那样专门戳漏洞的什么狗屁记者。
(1)无人机
王慧哲等[9]以民用无人机为背景,结合全源导航需要快速集成并重新配置任意导航传感器的要求,对全源导航的关键技术展开研究,构建了如图2所示的基于因子图的多传感器融合框架,其中涉及的传感器包括IMU、GPS、气压高度计、光流传感器、磁航向传感器、星敏感传感器。

图2 基于因子图的多传感器融合框架Fig.2 Diagram of multi-sensor fusion framework based on factor graph
在接收IMU观测信息后定义因子节点fIMU,连接tk和tk+1两个不同时刻的变量节点即导航状态xk和xk+1, 因子节点IMU可表示为
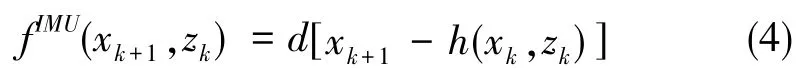
在tl时刻接收到GPS观测信息后,定义因子节点fGPS

同理,在其他时刻接收到高度计、星敏感器等传感器观测信息后,定义相应因子节点拓展因子图,根据相应的观测方程和代价函数进行变量节点的状态更新。实验以Matlab为平台实现对飞行器轨迹的设计,模拟不同传感器的数据输出以及对文中提出的算法进行仿真验证。运动轨迹仿真通过抬头、爬升、平飞、转弯、倾斜、俯冲等机动动作模拟飞行器真实的飞行状况,并且设置GPS在500s~1000s内不可用、星敏感器在800s~1200s内不可用、光流传感器在1300s~1400s内不可用,以模拟飞行过程中的故障情况。仿真结果表明,因子图算法能对异步异质传感器的数据进行有效融合,并适应传感器在运行过程中可用性发生变化的情况。
文献[10]以无人机MINS/BDS/磁罗盘/气压高度表组合导航系统为例构建了因子图信息融合模型,通过车载跑车试验采集导航传感器原始数据进行离线仿真,将因子图融合算法与分散式联邦滤波算法进行误差对比,验证了因子图算法作为无人机信息融合方法的可行性,并且该方法在高度定位以及航向角测姿上展现了更高的精度。
针对密集集群无人机的协同导航问题,文献[11]提出了一种基于因子图优化的无人机群协同导航方法,结合无人机自身的导航信息和无人机之间的测距信息,将无人机群协同导航信息融合问题转换成因子图模型,给出了基于消息迭代策略的因子迭代方法,为每架无人机建立局部因子图,实现了协同导航信息分布式处理和位置优化。仿真试验结果表明,所提出的方法可有效提高密集集群等多无人机应用场景下的定位精度。
(2)AUV
对于自主水下潜器(AUV)的水下组合导航信息融合技术,国内外众多研究学者作了大量的研究,其中的分布式Kalman滤波应用最为广泛。文献[12]则针对AUV所在水下复杂多变的环境与任务需求提出了基于因子图的AUV多传感组合导航算法,对捷联惯性导航系统、Doppler计程仪、磁航向仪、地形辅助导航设备进行建模,构建了基于因子图的信息融合框架。仿真结果同样表明,因子图方法能够连续稳定地输出较高精度的导航结果,有效实现了惯性导航系统与不同导航传感器的非等间隔融合,且具有很好的灵活性与扩展性。
文献[13]则提出了一种基于因子图的多AUV协同导航定位算法,根据当前时刻AUV的领航与跟航关系构建相应的变量节点、函数节点和因子图模型。之后,针对因子图中的消息传递形式推导了和积算法,随后对基于因子图的多AUV协同导航定位算法进行描述和推导。最后的仿真结果表明,算法可以有效估计出AUV的位置信息,且在弱噪声情况下的定位准确度要优于扩展Kalman滤波算法。另外,在大规模多AUV协同导航定位系统中增减AUV时只需添加对应的局部因子图模型,因此因子图方法具有很好的扩展性。
(3)卫星拒止条件下的应用
目前,几乎所有军用和民用系统都依靠基于卫星的组合导航系统来获取导航定位信息。但卫星信号在复杂环境下容易受到干扰,在室内、地下等环境中衰减严重。因此,针对卫星导航在一些特定环境和条件下的局限性,国内外学者均对卫星信号拒止环境下的新导航技术展开了多项研究,基于因子图的导航技术就包括其中。文献[14]提出了一种基于因子图协同定位辅助的单星定位方法,利用多个定位目标之间的高精度测距信息建立协作因子图,并利用该协作因子图辅助单星定位系统的定位结果,从而提高定位精度。
文献[15]定义了IMU、BDS和里程计量测因子后构建了基于因子图的多传感器融合框架。在跑车实验中,令五个时间段内北斗卫星信号丢失,在行驶600s后导航精度依旧可以得到有效保障,卫星拒止环境下可以将剩余传感器信息快速有效融合,实现了多传感器的即插即用。
2.4 改进的因子图算法

当GNSS、OD的测量频率与系统输出频率不同以及存在时延时,文献[16]构建了如图3所示的因子图模型。
上述构建组合导航系统因子图模型的过程表明,组合导航系统中各传感器的因子节点在因子图模型中是相互独立的、互不影响的。当GNSS突然失效时,只需要抑制GNSS因子节点的继续添加,便转换为INS/OD因子图模型;而当GNSS变为有效时,只需要重新加入GNSS因子节点,便恢复为INS/GNSS/OD因子图模型。这说明采用因子图模型描述组合导航问题可以灵活地处理传感器有效性的动态改变,基于因子图的组合导航算法具有很强的灵活性和实时性。

图3 INS/GNSS/OD存在时延时的因子图模型Fig.3 Factor graph modelof time delay in the presence of INS/GNSS/OD
文献[17]提出了如下所示的自适应因子

式(8)中,Φ(Λk)为自适应可信度调节函数,其值为[0,1]之间的标量。从因子图拓扑网络角度来看,基于可信度的值,可以启用或禁用与其关联的约束边,从而实现在拓扑中加入或删除的操作。构建新的自适应因子图模型,如图4所示。

图4 自适应因子图模型Fig.4 Diagram of adaptive factor graph model
在仿真实验中,分别采用传统因子图算法和基于可信度的自适应因子图算法与真实轨迹及惯性/卫星子系统轨迹对比,尤其通过比较卫星拒止区域的定位精度可以看出:基于可信度的自适应因子图算法能够自适应调整因子图拓扑结构,从而保证了复杂动态场景下多源融合导航算法的鲁棒性和环境自适应性,提升了自主无人系统跨场景导航模式切换和连续可靠的导航定位能力。
在因子图算法中,应用Bayes推断进行状态量估计的范围可以是整个因子图网络。但是,遍历估计的方法使得算法在运行过程中的计算量不断增大,而且最新得到的观测值对早期变量估计准确性的提高也并不显著。因此,通过对因子图的优化范围加窗,即限定参与优化的因子节点范围,能够有效减少算法计算量,提高算法的效率。
滑动窗使得因子图的全局最优化过程仅发生在最新生成的若干个节点间,它的引入不仅提高了融合算法的估计速度,而且还减少了算法的计算量。


图5 基于滑动窗口的因子图模型Fig.5 Diagram of factor graph model based on sliding window
3 总结与展望
如今,单一的导航系统已经不能满足对导航精度以及抗干扰能力的需求,组合导航技术成为载体导航与定位的主流方法[19]。与单个传感器信息相比,多种传感器组合信息显然能够提供更精确、更具鲁棒性的导航结果[20]。基于因子图的多传感器信息融合导航算法可以方便地融合多种传感器的数据,可以满足传感器的即插即用和快速配置。从对因子图算法的可行性进行分析到其在无人机、水下潜器等上的应用再到多种改进的因子图算法的提出,国内外已经开展了很多关于因子图算法的研究,本文也对其进行了一定程度的阐述。但由于理论水平和技术水平有限,目前的研究仍然存在如下的一些改进空间:
1)因子图算法中,随着时间的增长,图中的变量节点也逐渐增加,进行计算的时候,数据维度也逐渐增加,这需要消耗大量的空间资源和时间成本[21]。因此,需要对此进一步进行研究从而提高导航系统的实时性。
2)目前,基于因子图的多传感器融合算法大多都是基于松耦合结构的,建立紧耦合融合框架理论上可以提高导航精度,可以作为接下来的一个发展方向。
因子图算法在即插即用等方面的巨大优势注定它存在很大的发展空间和实用价值[22],但迄今为止针对因子图算法的研究仍只停留在实验仿真阶段,尚未应用于实际系统,同时研究也存在诸多问题,因此仍需要大量的理论工作和工程实践。

