基于ISM模型的地下环形隧道通行能力影响因素研究

肖新波 马 腾 焦宇帆 胡美娜

(1.中国市政工程中南设计研究总院有限公司 武汉 430010； 2.长安大学运输工程学院 西安 710064)

近年来，随着城市化的快速发展，土地利用趋于饱和与交通拥堵日益严重相冲突、车辆运行带来的噪声和废气污染等问题难以解决，同时，在地下空间规模化发展、轨道交通快速发展的多重背景下[1]，人们逐渐将目光转向地下交通，这促进了地下道路建设的迅速发展。地下环形隧道(以下简称地下环隧)作为城市地下空间开发的重要组成部分，其建成与使用能够打造立体化城市交通网络，减少道路系统的功能重叠，提升区域交通的畅通性、便捷性。同时，地下环隧可以与城市大型地下车库之间设有连接通道，这也为解决中心城区停车难的问题提供了新的手段。对于节约土地资源、打造高质量城市用地属性有着极为重要的意义[2]。

目前，国内外学者在城市道路、高速公路的通行能力方面已有不少的研究，大多从交通环境[3-4]、人为因素[5]、交通管理[6]、气候条件[7]等方面着手，深入分析其对道路通行能力的影响程度及相互关系。但对城市地下环隧的研究并不深入，尤其是在地下环隧的通行能力方面。

开展地下环隧通行能力影响因素的研究有利于从全局角度着眼影响因素-通行能力的关系，研究地下环隧运行状况与通行能力，对提高地下环隧的服务水平与提升驾驶员满意度具有重要的现实意义，除此之外，探究影响地下环隧通行能力因素的主次关系也有利于为地下环隧的设计提供参考。

解释结构模型(interpretative structural modeling,ISM)又被称为ISM分析法，是John.N.Warfield在1973 年为了分析经济系统而开发的分析方法，可以解决复杂的系统问题[8]。引入ISM模型可将系统复杂的影响因素间关系进行定性分级分层，解释各影响因素间的相互影响、相互制约、相互联系。本文采用ISM分析法，对城市地下环隧通行能力的影响因素进行归类和分析，解释各影响因素之间的相互关系及其影响程度，以期提高城市地下环隧的通行效率。

1 地下环隧的主要影响因素

地下环隧作为一个完整的交通系统，主要包括出入口、隧内路段、转弯路段和服务接入点及各段连接处，而对城市地下环隧通行能力影响因素的分析是一个复杂的过程。目前，地面道路通行能力的影响因素一般选取道路、交通、控制、环境条件等。道路条件通常是指道路的几何特征，包括车道数、侧向净宽、平纵线形等；交通条件则是指道路交通特征，包括车型比例、交通流量等；控制条件是指道路交通管制设施的形式和设置，比如，交通信号的设置、标志标线的设置、车道的使用管理等；环境条件大多指气候条件、光照环境等等。考虑到地下环隧与地面道路的差异性，引入地下环隧出入口数量、服务区接入点车道长度等作为其通行能力的影响因素。在参考国内外有关地下隧道、高速公路隧道等文献[9-10]的基础上，通过与交通规划与设计专业技术人员及有关专家的沟通和交流，确认了影响城市地下环隧通行能力的主要影响因素，详见表1。

表1 城市地下环隧通行能力的主要影响因素

以上影响城市地下环隧的因素体系中，部分因素之间存在相互影响、相互制约的关系。如车道数与出入口数量的增加可吸引更多的车辆进入地下环隧，而车辆数的增加引起流量的增加，当地下环隧的车辆数达到一定程度时，会引起交通流密度过大，从而引起车速的降低，造成延误。众多影响因素之间的关系复杂模糊，很难对其进行准确的描述，而ISM模型可有效地解决此类问题。

分析各影响因素之间的相互关系，建立关联模型，ISM分析法常使用V、A、X、O来表示其相互联系的方向性，并建立二元关系表。其中：V为该行代表的影响因素影响该列代表的影响因素；A为该行代表的影响因素受该列代表的影响因素的直接影响；X为该行与该列代表的影响因素直接存在相互影响的双向关系；O为行与列代表的影响因素直接不存在关联。地下道路影响因素二元关系表见表2。

表2 地下道路影响因素二元关系表

2 建立ISM模型

将二元关系表转化为邻接矩阵A，转换原则为：当表2中元素为V时，aij=1且aji=0；当元素为A时，aij=0且aji=1；当元素为X时，aij=aji=1；当元素为O时，aij=aji=0，另外对角元素为0。转化结果如下列矩阵A所示。

邻接矩阵表示的是各因素之间的直接影响关系，将邻接矩阵A根据布尔运算规则，迭代终止条件如下。

令A(1)=A+E，A(2)=(A+E)2，…，A(K)=(A+E)K。

当A(K+1)=A(K)≠A(K-1)时，迭代终止，此时可得到可达矩阵M。

在可达矩阵M中，若mij=1(或mji=1)，表示行对列(或列对行)有直接或间接影响，若mij=0(或mji=0)则表示行对列(或列对行)相互独立无影响关系，依据ISM的规范方法，要确定区域内要素所处的层次地位，即级位划分，首先需要进行区域划分。得到每个元素的可达集R(Si)、先行集A(Si)、共同集C(Si)。在对城市地下环隧通行能力影响因素的可达矩阵进行分析后，得到该系统各要素的可达集、先行集、共同集表见表3。

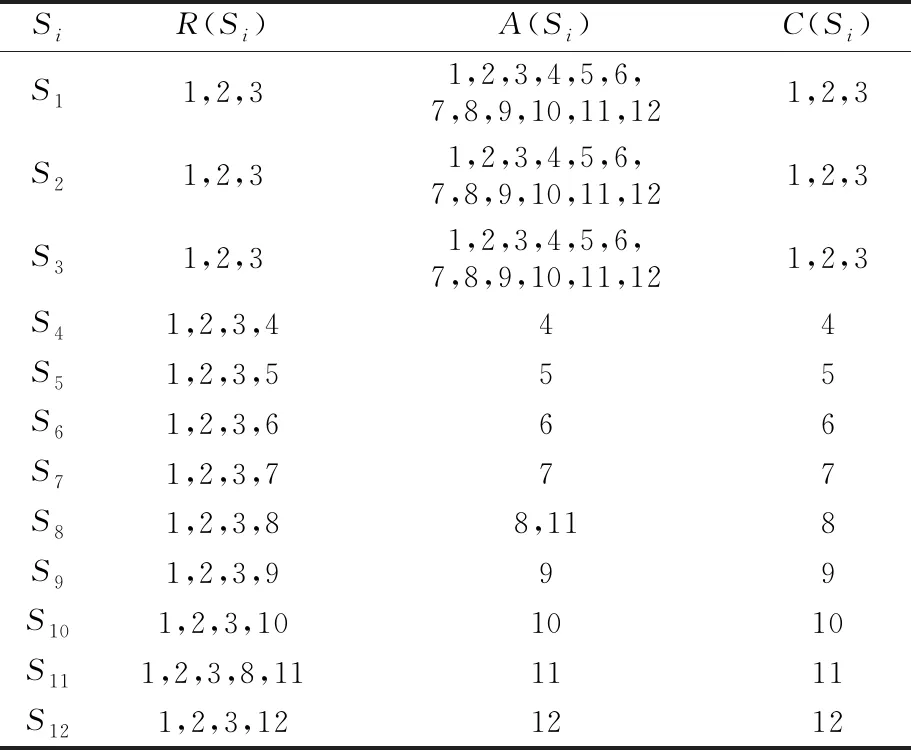
表3 ISM模型的可达集、先行集与共同集

级位划分的基本方法是：找出整个系统要素集合的最高级要素后，将该要素所在的行和列划去，再求得剩余要素集合中的最高要素。依此类推，直到确定出最低一级要素集合。依照级位划分的方法，求得城市地下环隧通行能力影响因素系统的级位划分结果为：L1={S1，S2，S3}，L2={S4，S5，S6，S7，S8，S9，S10，S12}，L3={S11}。依据上述的分析结果，建立城市地下环隧通行能力影响因素多级递接结构模型，该模型中影响因素多级递接结构图见图1。

图1 城市地下环隧通行能力影响因素多级递接结构图

3 ISM模型分析与建议

由图1可知，城市地下环隧的影响因素体系可分为3层。这3个层级反映了地下环隧影响因素之间的关系，根据层级关系可将其划分为车流特性因素、环境因素与天气因素，具体分析如下。

3.1 ISM模型分析

第一层的车流特性条件包括车速、流量与密度3个因素。地下环隧作为一个完整的交通流系统，交通流三要素是直接衡量地下环隧通行能力的指标，同时在很大程度上，速度、密度与流量之间的关联与制约关系也使地下环隧的通行能力变化复杂。

第二层级因素众多，主要包括：侧向净空、光照、服务接入点车道长度、出入口数量、车型比、曲率、车道数、信号灯设置，此类因素包括道路条件、管制条件、交通条件等，为了能够更好地对其进行分析，将其统一归类为环境条件。第二层级的影响因素一旦被确定，交通设施的通行能力即可确定，任一环境因素的改变都会引起地下环隧通行能力的改变。

第三层级影响因素为天气，将其归类为气候条件。地下环隧不同于传统的城市道路与高速公路，地下环隧呈现的是狭窄的视觉空间，出入口内外行车环境与亮度的变化，以及“黑洞效应”与“白洞效应”的发生会引起驾驶者生理心理行为的变化，从而引起驾驶行为的改变。微观交通行为的变化引起宏观交通流的变化，从而对通行能力产生影响。另外，雨雪天气下地下环隧进出口处受坡度的影响，安全性降低，驾驶员趋于降低进入地下环隧的速度，此时更容易发生拥堵，造成延误。

由上述分析可见，ISM模型将影响地下环隧通行能力错综复杂的因素进行了有效划分，将其分为3个层级，每个层级包含的指标代表的含义不同，其影响地下环隧的通行能力的程度及原理也不同。第一层级的影响指标通过控制地下环隧的动态车辆输入，直接影响整个地下环隧的通行能力，而第二层级则聚焦于环境影响，通过影响驾驶员驾驶行为而间接改变地下环隧通行能力。第三层级的影响机制附着于第二层级的同时，具备其特殊性。

3.2 建议

1) 通过使用ISM模型，对影响地下环隧通行能力的因素进行分层，整体而言，第一层级的影响最直接最主要，因此在对地下环隧整体通行能力进行控制时，第一层级指标的重要度最高。

2) 对地下环隧交通流三要素的分析与判断，得出地下环隧交通流运行状况最佳的车速、密度与流量，并以此作为交通管制手段的依据之一，通过限速限行、优化地下环隧及其上游的信号灯相位设置、改变地下环隧上游绿波带等手段，使地下环隧中的交通流处于和谐高效的运行状态中。

3) 在设计城市地下环隧时，充分考量环境因素对其通行能力造成的影响，充分挖掘地下环隧交通基础设施的潜力，最大程度为驾驶员提供最佳的驾驶环境，在保障安全的前提下，使地下环隧的实际通行能力最接近理想通行能力。

4) 在考虑气候条件对地下环隧造成的影响时，可将不同天气情况下最佳光照强度进行量化，通过对地下环隧出入口处光照的智能调节，降低“黑洞效应”“白洞效应”对驾驶员视觉改变造成的影响，使出入口段的车流运行状况更加稳定。

4 结语

本文对城市地下环隧影响因素间关系进行探究，通过定性描述二元影响关系与矩阵定量分析的方式建立ISM模型，将12个影响因素分为3个层级：车流特性条件、环境条件和气候条件，并构建层次递阶结构图。结果表明，交通流三要素为地下环隧通行能力的直接体现，而环境条件与气候条件造成的影响也是不容忽视的。为进一步证实各影响因素对地下隧道通行能力的影响并获得定性影响程度指标，尤其是针对车速、密度与交通量等因素，下一步的研究可以利用实际调查所得的地下环隧数据，建立通行能力影响模型，从而为地下环隧的设计及管制手段提供可靠的决策基础。