典型倒装式基层沥青路面结构力学响应对比研究

牛敏强 王安怀 邓明超 苑苗苗

(1.广东省南粤交通仁博高速管理中心新博管理处 惠州 516899；2.广东省南粤交通投资建设有限公司 广州 510623； 3.华南理工大学广州学院 广州 510800)

半刚性基层沥青路面结构是我国高等级公路最常用的一种路面结构形式，由于半刚性基层具有刚度大、强度高、材料来源丰富及价格经济等优点，已在我国路面结构中广泛使用[1-4]。然而，经过多年的实际工程应用，半刚性基层沥青路面的缺陷也逐渐显露出来。在温度、湿度等综合因素作用下，半刚性基层容易出现温缩、干缩疲劳开裂，在行车荷载作用下裂缝逐渐贯通基层并反射到沥青面层，从而导致沥青面层出现一些早期损害[5-7]。针对该问题，国内外道路工作者提出了较多解决方法，其中一种方法是采用倒装式基层沥青路面结构，即在半刚性基层与沥青面层之间增设一层级配碎石基层，目的是减少由于半刚性基层开裂引起的反射裂缝[8-10]。该种沥青路面结构在不增加面层的厚度情况下，同时使得半刚性基层下卧更深，改善了路面受力特性，取得了较好的应用效果。

在沥青面层与半刚性基层之间设置一层级配碎石层或者ATB和级配碎石层，路面结构受力特性发生了较大变化。为了更好地分析并了解该种路面结构的受力变化，深入了解倒装基层沥青路面结构力学机理，本文依托广东省境内新博高速试验段的3种倒装式基层沥青路面结构形式，采用ABAQUS有限元工具，分别模拟了沥青路面在双轮标准轴载作用下的力学响应，分析3种倒装基层沥青路面结构的各自受力特性，为倒装基层沥青路面结构组合设计提供参考。

1 有限元模型建立

本研究基于新博高速试验段的3种倒装基层沥青路面结构进行分析，路面结构组合及结构层材料参数见表1。

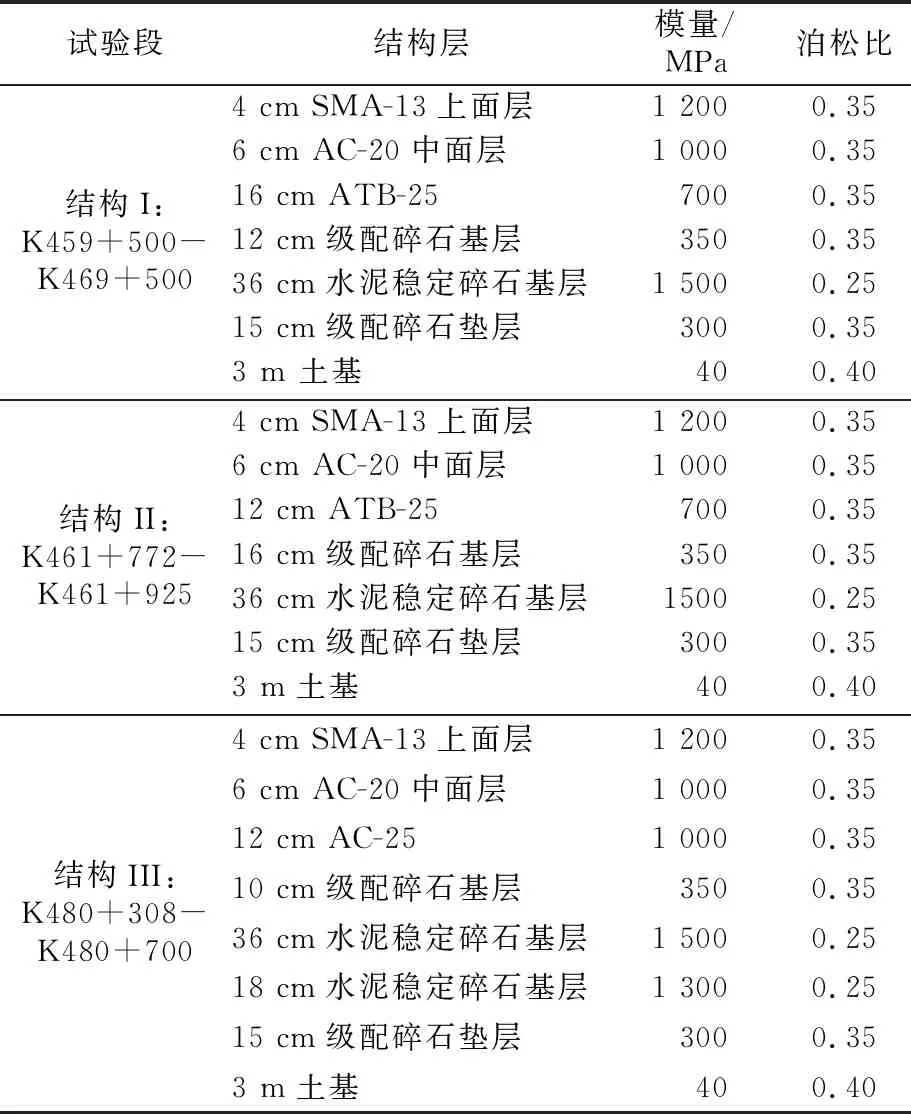
表1 试验段倒装路面结构层厚度及材料参数

为简化计算，将各结构层假定为连续的、完全弹性的、各向同性的匀质体，结构层之间接触假定完全弹性，模型底面为完全约束，侧面仅约束垂直于侧面的水平位移而表面无约束。路面模型在水平方向和深度方向取其有限尺寸，其中长度和宽度各为5 m，土基厚度为3 m。

沥青层、基层、垫层及土基采用三维实体单元(C3D8R实体缩减积分单元)进行离散处理，划分有限元网格，网格划分的密度选择自由划分。结构I模型单元数量为47 502，节点数量为58 800；结构II模型单元数量为47 502，节点数量为58 800；结构III模型单元数量为53 157，节点数量为66 000。为了便于模型计算，轮胎与路面接触面理想化为18.9 cm×18.9 cm的正方形，双轮中心距32 cm，计算轴载为标准轴载BZZ-100，轮胎接地压为0.7 MPa。具体的有限元模型图见图1。

图1 三维有限元模型

2 路面结构力学响应对比分析

本研究选用的力学响应计算点位置图见图2。

图2 力学响应计算点位置示意图

其中：A点为车轮中心；B点为车轮迹边缘；

C点为两轮胎中心；D点为B点与C点的中点(称为车轮隙r/4处)。基于建立的模型对3种倒装基层沥青路面结构进行力学分析，并对比3种模型的路表弯沉、沥青层层底拉应变、半刚性基层层底拉应力，以及土基顶面压应变。

2.1 模型验证

本研究以路表轮胎中心处弯沉值作为验证指标，通过对比试验段建成后的实测弯沉值和有限元模型计算弯沉值，验证本文三维有限元模型的可行性和有效性。通过ABAQUS有限元软件计算3种结构的路面弯沉计算云图见图3。

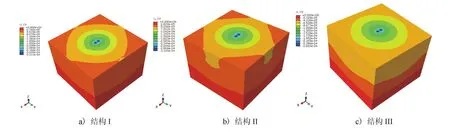
图3 3种倒装结构路面弯沉云图(单位：m)

利用落锤式弯沉仪(FWD)对3种结构的试验段路表弯沉值进行检测，倒装结构路表弯沉值数据见表2。

表2 3种倒装式基层沥青路面结构路表弯沉值对比 0.01 mm

由表2可知，结构I和结构II的路表实测弯沉值和计算弯沉值非常接近，而结构III的两者之间的弯沉值存在一定差异，主要原因是实测弯沉测量于2018年12月份开展，温度偏低，各结构层材料模量偏大，但实测弯沉只比计算弯沉减少8.8%。因此，可以认为3种有限元模型具有较高的可靠性，计算结果能较好地满足分析要求。

2.2 路面弯沉对比分析

分析通过双轮中心距模型边缘不同距离处的路面弯沉值，路面弯沉分析结果见图4。

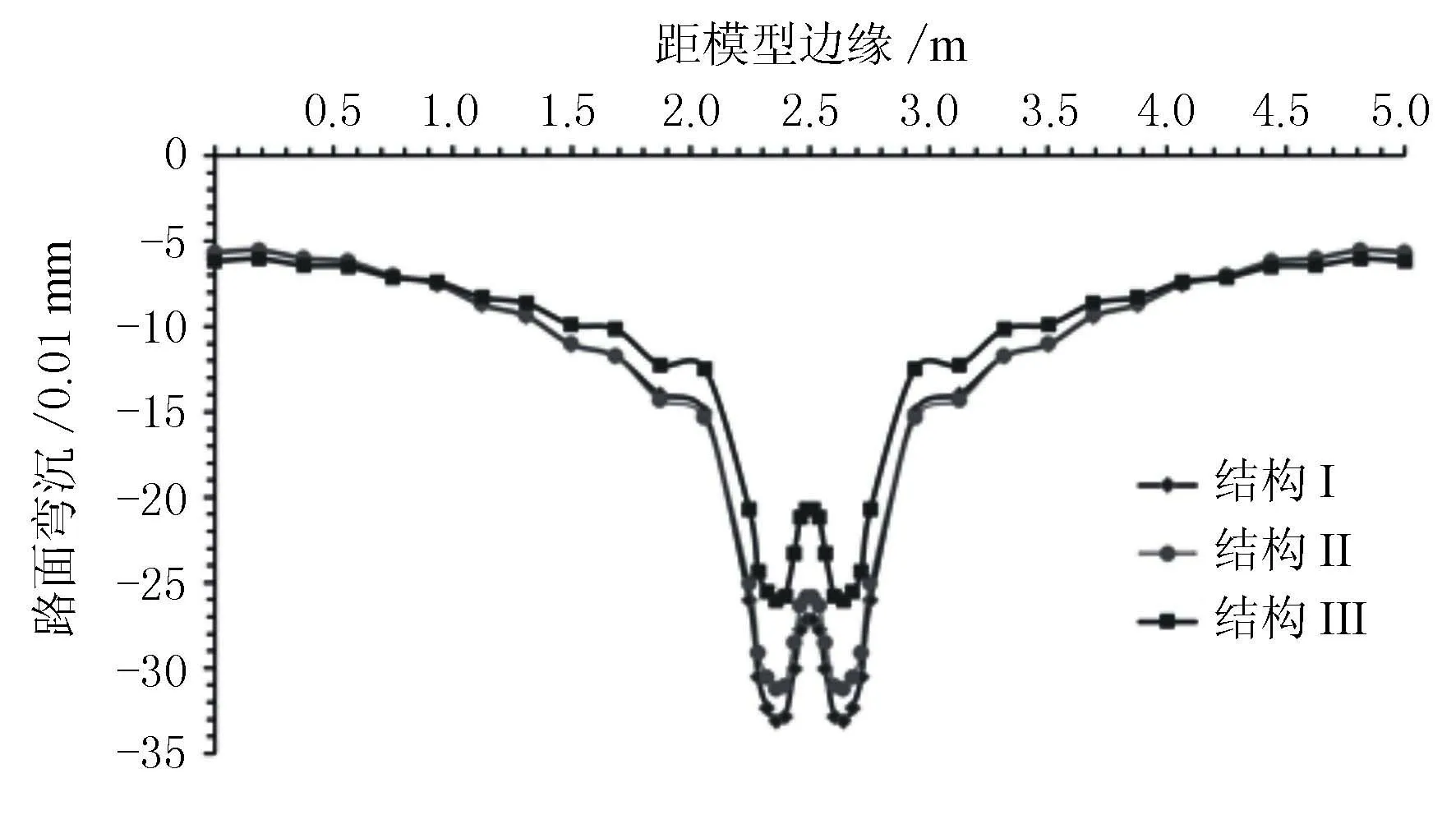
图4 路面弯沉

由图4可知，路面弯沉出现在2个轮胎中心处，结构I的轮胎中心处最大弯沉为33.1(0.01 mm)，结构II的轮胎中心处最大弯沉为31.3(0.01 mm)，结构III的轮胎中心处最大弯沉为26.0(0.01 mm)。由此可见，结构I和结构II的路面弯沉非常接近，2种结构区别在于ATB-25和级配碎石基层的厚度不一致，但两层总厚度及模量一样，从降低工程造价角度来说，可适当减少ATB层的厚度增加级配碎石基层厚度但保持两层总厚度不变。相比结构II，结构III最大的区别在于增加了1层18 cm的水泥稳定碎石底基层，其计算的路面弯沉下降了16.9%，对于减少路面弯沉效果明显。因此，从路面最大弯沉对比来看，结构III优于结构I和结构II，而结构I和结构II区别不大。

2.3 沥青层层底拉应变对比分析

3种路面结构模型沿行车方向的水平应变云图见图5。

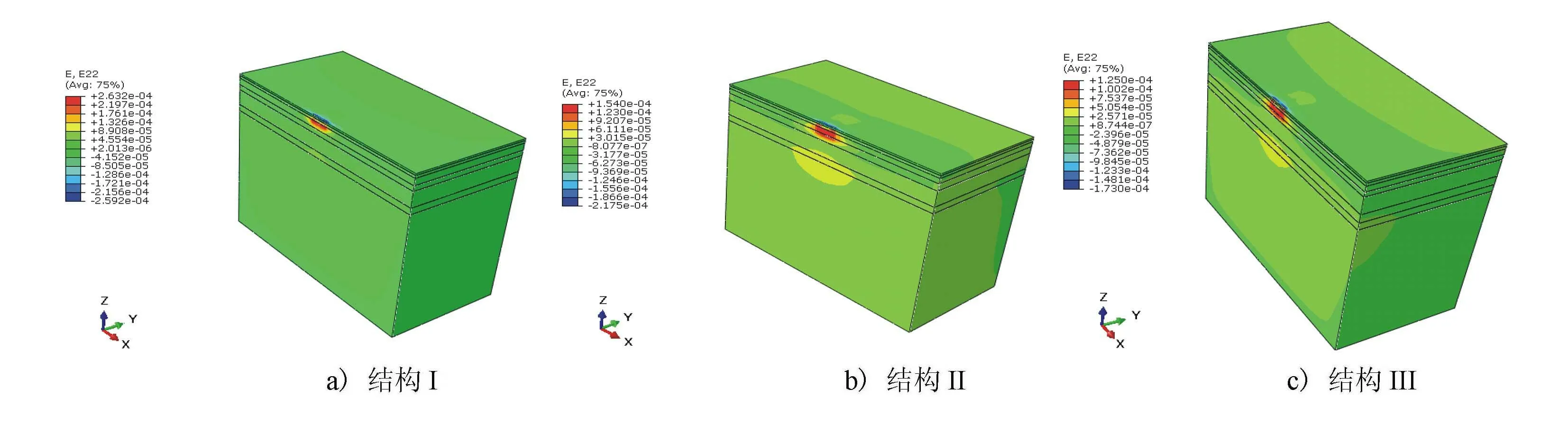
图5 路面结构剖面应变云图

由图5可见，结构I和结构II的沥青面层最大层底拉应变出现在AC-20沥青层层底，且处于轮胎荷载中心正下方；结构III的沥青面层最大层底拉应变出现在ATB-25沥青层层底，但处于车轮迹边缘正下方。分别分析轮胎荷载中心正下方AC-20和ATB-25沥青层层底距模型边缘不同距离处的拉应变，比较3种路面结构的差异，分析结果见图6。

图6 AC-20沥青层层底沿行车方向水平应变

结构I的沥青层层底最大拉应变为256.8×10-6，结构II的沥青层层底最大拉应变为235.9×10-6，结构III的沥青层层底最大拉应变为124.4×10-6。结构II的沥青层层底最大拉应变较结构I减少了8.1%，而结构III的沥青层层底最大拉应变降低了51.6%。因此，结构III的面层抗疲劳性能最优，而结构I和结构II差异较小。

结构I和结构II的ATB层沿行车方向水平应变见图7所示。

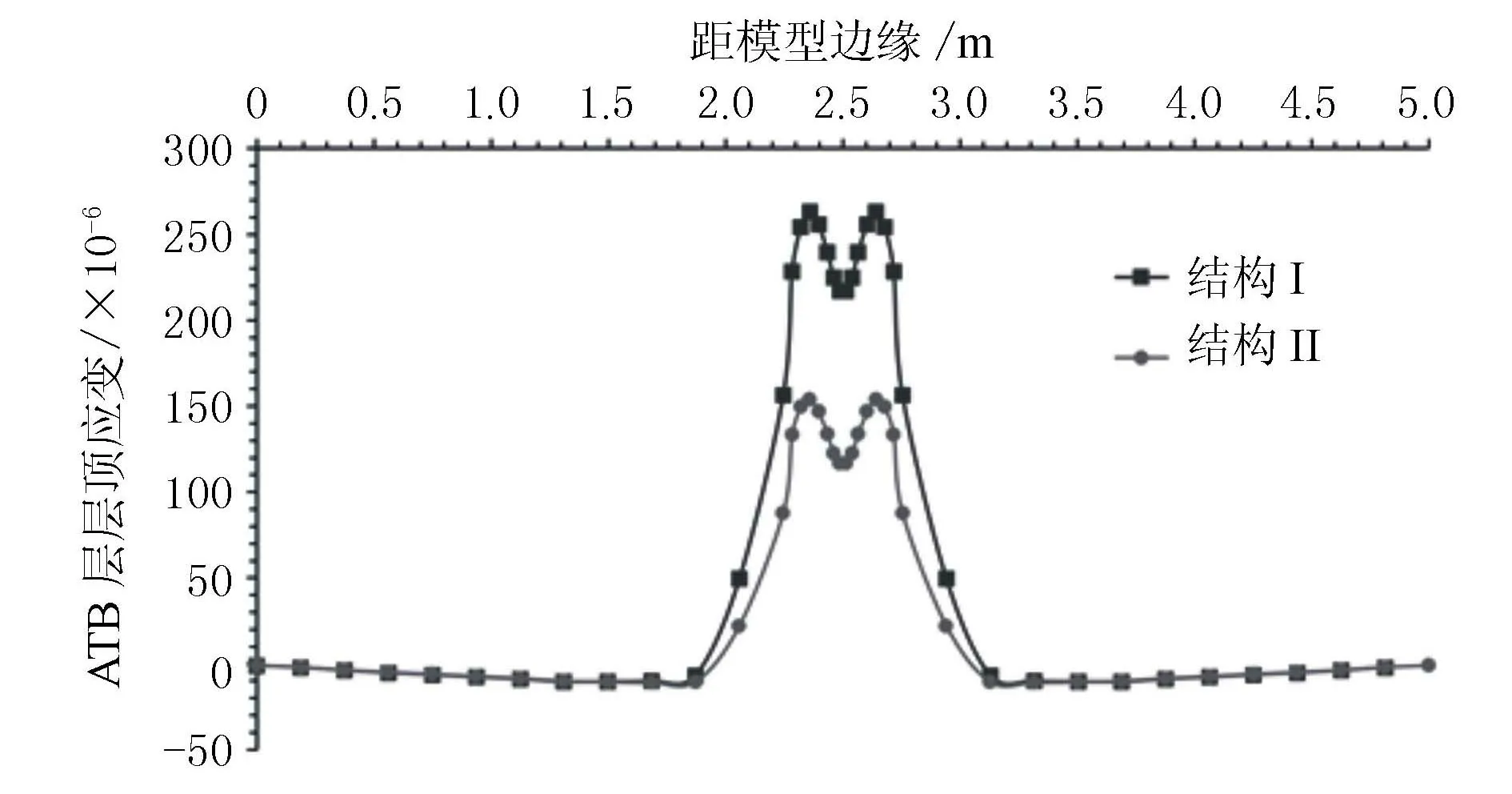
图7 ATB层沿行车方向水平应变

由图7可见，对于结构I，沿行车方向的最大水平拉应变出现在ATB层上表面，为263.2×10-6。对于结构II，沿行车方向的最大水平拉应变出现在AC-20沥青层层底，而对于结构II的ATB层沿行车方向的最大水平拉应变出现在ATB层上表面，其值为154×10-6。换句话说，要求结构I的AC-20和ATB层均具有较好的抗疲劳性能，结构II的AC-20层具有较高的抗疲劳性能。

2.4 半刚性基层层底拉应力分析

3种路面结构模型沿行车方向的水平应力云图见图8。

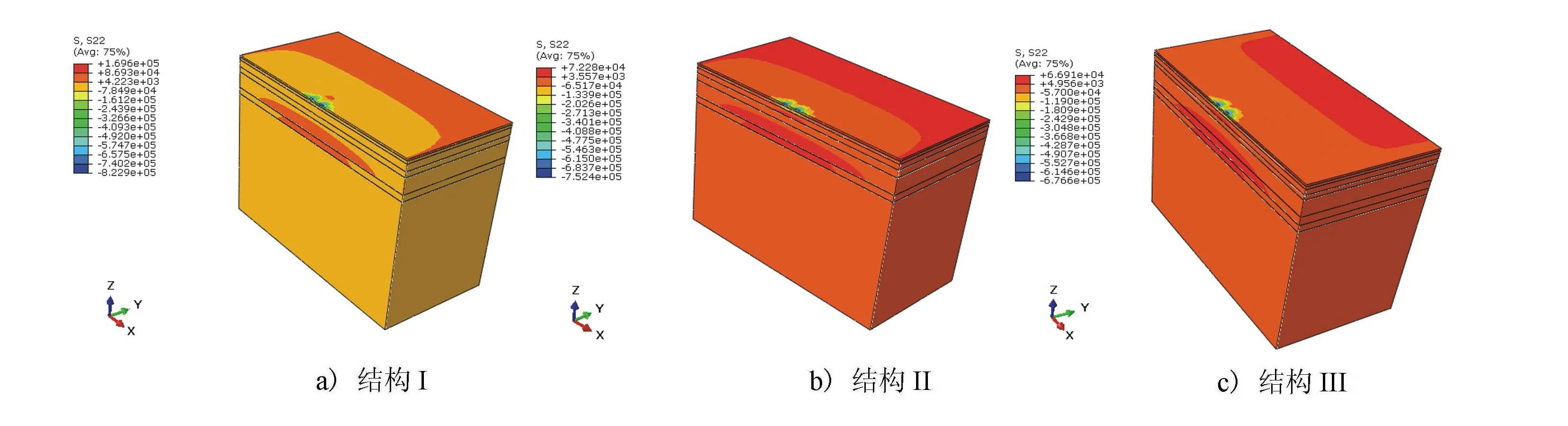
图8 路面结构应力云图(单位：Pa)

由图8可见，半刚性基层最大拉应力出现在半刚性基层层底。双轮中心距模型边缘不同距离处的半刚性基层层底拉应力见图9。

图9 半刚性基层层底沿行车方向水平拉应力

由图9可见，半刚性基层层底沿行车方向的最大拉应力出现在2个轮胎中心正下方，结构I和结构II的半刚性基层层底最大拉应力几乎相等，最大值分别为0.072 6 MPa和0.072 3 MPa。结构III的半刚性基层层底最大拉应力为0.050 9 MPa。虽然结构III的半刚性基层层底最大拉应力较结构I和结构II减少30%左右，但3种结构的半刚性基层层底最大拉应力均非常小。

2.5 路基顶面竖向压应变分析

3种路面结构模型路基顶面竖向压应变云图见图10。双轮中心距模型边缘不同距离处的路基顶面竖向压应变见图11。

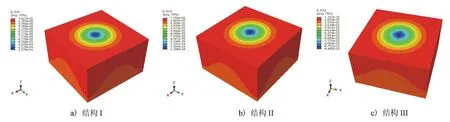
图10 路基顶面竖向压应变云图

图11 双轮中心距模型边缘不同距离处的路基顶面竖向压应变

由图10、11可见，路基顶面竖向最大压应变出现在2个轮胎中心正下方，结构I和结构II的路基顶面竖向最大压应变差别不大，最大值分别为127.9×10-6和130.6×10-6。结构III的路基顶面竖向最大压应变为94.5×10-6。结构III的路基顶面竖向最大压应变较结构I和结构II分别减少26%和28%左右，这主要是由于结构III设置了2层半刚性基层，因而具有较好的荷载扩散能力，路基顶面竖向最大压应变相对其他2种结构降低明显。

3 结语

本文依托实际工程对3种典型倒装沥青路面结构的力学响应进行对比分析，通过ABAQUS有限元软件建立3种倒装结构的力学模型，在标准轴载BZZ-100下，进行了沥青路面结构力学模拟计算，对比分析了3种倒装沥青路面结构的路面弯沉、沥青层层底拉应变、ATB层层顶拉应变、半刚性基层层底拉应力及路基顶面竖向压应变，得到以下结论。

1) 结构I、结构II及结构III的轮胎中心处最大弯沉分别为33.1(0.01 mm)，31.3(0.01 mm)，26.0(0.01 mm)，从路面最大弯沉对比来看，结构III优于结构I和结构II，而结构I和结构II区别不大。

2) 结构I、结构II及结构III的沥青层层底最大拉应变分别为256.8×10-6，235.9×10-6，124.4×10-6。因此，结构III的面层抗疲劳性能最优，而结构I和结构II差异较小。

3) 结构I和结构II沿行车方向的最大水平拉应变出现在ATB层上表面，其值分别为263.2×10-6，154×10-6。因此，结构I的AC-20和ATB层均应具有较好的抗疲劳性能，结构II中需要AC-20层具有较高的抗疲劳性能。

4) 结构I、结构II及结构III的半刚性基层层底最大拉应力分别为0.072 6，0.072 3，0.050 9 MPa，3种结构的半刚性基层层底最大拉应力非常小。

5)结构I、结构II及结构III的路基顶面竖向最大压应变分别为127.9×10-6，130.6×10-6，94.5×10-6，结构III的路基顶面竖向最大压应变相对其他2种结构降低明显，因而具有较好的荷载扩散能力。