基于ARIMA模型的城乡居民收入差距预测分析——以湖北省为例

吴 琴

(湖北民族大学 数学与统计学院，湖北 恩施 445000)

改革开放四十年来，随着我国经济持续快速发展，居民收入水平随之不断提高，但是城乡居民之间的收入差距整体上却在持续扩大。[1]城乡关系的不协调不仅有碍于社会公平与和谐稳定，而且也不利于经济的健康可持续发展。[2-4]美国经济学家库茨涅兹曾提出了著名的倒U型理论，即收入分配差距会随经济发展进程呈现倒U型形状，[5]那么我国城乡居民收入差距未来的走势是否会伴随经济增长到达倒U曲线的拐点然后呈现下降趋势呢？基于此，探究城乡居民收入差距变化的内在规律具有重要的理论和现实意义。湖北省作为中部大省，是长三角经济带的重要发展区域，也是国家中西部战略发展的龙头省份。因此，本文选取湖北省城乡居民收入的时间序列数据，运用ARIMA 模型对两者差距进行分析和预测，为研究各地区城乡居民收入差距问题提供借鉴。

目前，针对城乡居民收入差距问题，学者们采用的方法主要有指数平滑法、人工神经网络模型、灰色预测法、ARMA模型等，[6-8]研究思路大都是将城镇居民收入和农村居民收入作差或作比，然后对差值或比值序列的趋势进行分析和预测，[9]如田垠采用灰色预测和神经网络的组合预测模型对我国城乡居民人均收入绝对差距进行分析和预测，得出的结论是我国城乡居民收入差距在未来两年会持续增长；[10]龚承刚、王梦、谢航采用的是ARIMA模型对湖北省城乡居民收入比进行分析和预测，得到的结论是湖北省城乡居民收入差距将会小幅度缩小。[11]但考虑到城镇居民收入和农村居民收入两个序列虽有一定的内在相关性，但也都有各自的发展规律，为了保留各自的特点，提高预测精度，本文采取的思路是分别建立农村居民收入和城镇居民收入的ARIMA模型，然后分别进行预测，最后将预测结果作差和作比，得出城乡居民收入差距的发展趋势。

一、湖北省城乡居民收入差距的现状分析

本文选取的城乡居民收入指标分别为城镇居民人均可支配收入和农村居民人均纯收入，[12]样本区间为1991—2019年，其中2018年以前的数据来源于湖北省各年统计年鉴，2019年的数据来源于湖北省统计局发布的报告。由相关数据得到图1和图2。

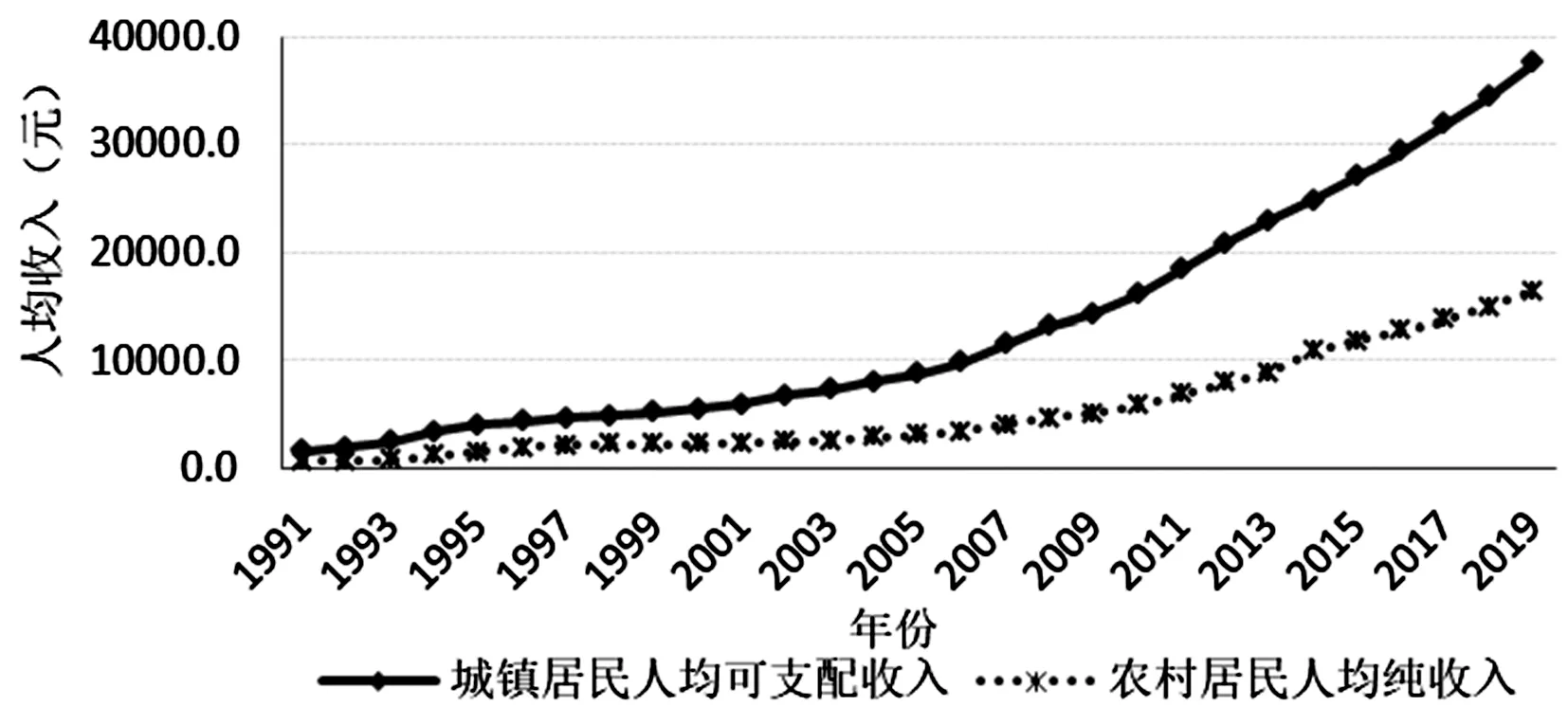
图1 湖北省城乡居民收入趋势图

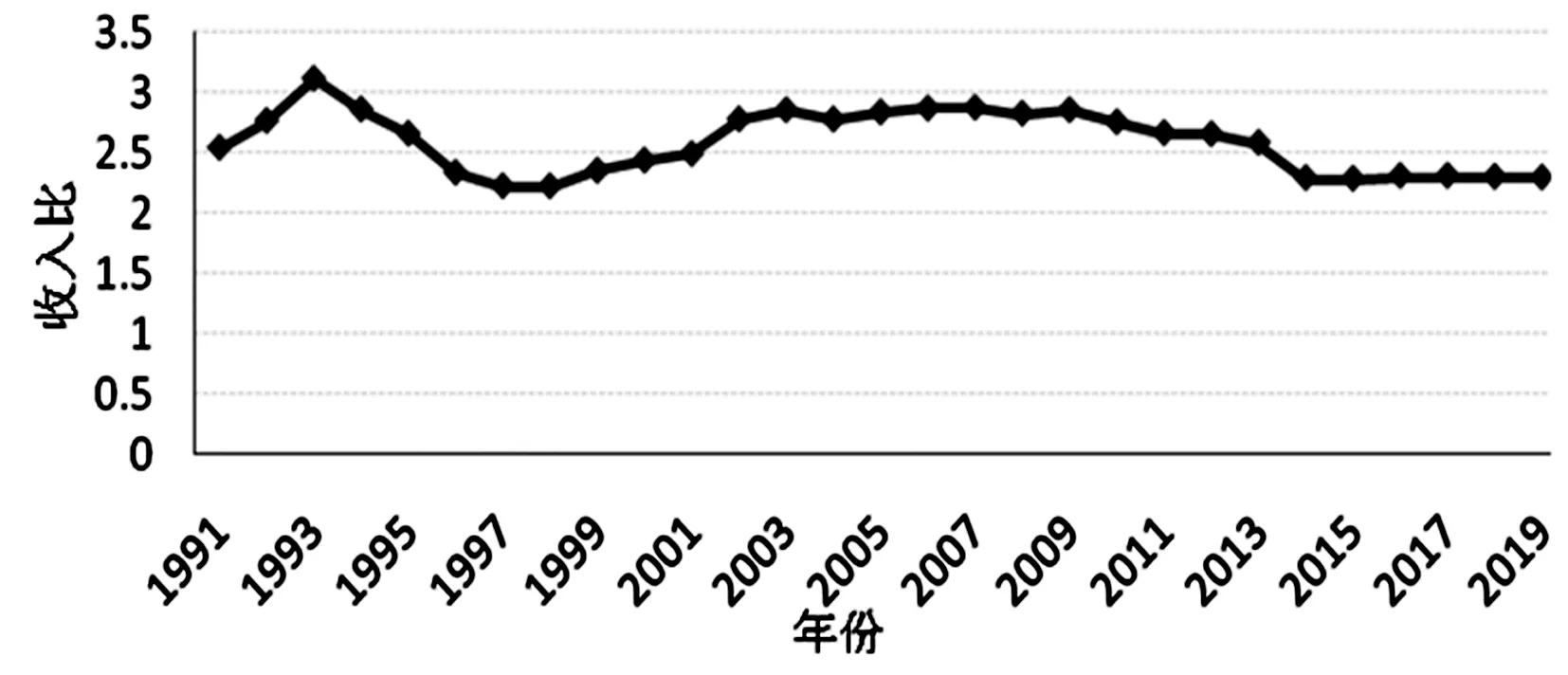
图2 湖北省城乡居民收入比

由图1可知，1991—2019年湖北省城乡居民收入逐步提升，其中城镇居民人均可支配收入由1991年的1 592.9元增加到2019年的37 601.6元，年均增长率11.95%；农村居民人均纯收入由1991年的626.92元增加到2019年的16 385.74元，年均增长率12.36%。湖北省城乡居民收入绝对差距呈逐步扩大趋势，但农村居民收入增长率快于城镇居民收入增长率。

由图2可知，从相对收入差距来看，城乡居民收入比呈小幅波动，其中：1991—1993年呈上升趋势，1993年达到最大值3.1，之后经历“逐渐下降—平稳波动”阶段，2012年后缓慢下降，在2016—2019年稳定在2.3左右，但与发达国家城乡居民收入比1.5，及世界劳工组织公布的1.6的标准相比，湖北省现阶段城乡收入比相对较大。若考虑城镇居民隐形福利收益，城乡居民收入实际差距可能更大。

二、基于ARIMA模型的预测分析

1.ARIMA模型

ARIMA模型全称为差分自回归移动平均模型，是由Box和Jenkins提出的专门用于非平稳时间序列分析和预测的一种方法，也是时间序列分析中最常用到的线性模型之一，适用于短期预测。ARIMA(p，d，q)模型的表达形式如下：[13](P142-145)，[14](P119-128)

(1)

式(1)中，▽=(1-B)，B表示为延迟算子，d表示为使非平稳时间序列成为平稳序列所做的差分次数；Φ(B)=1-φ1B-…-φpBp，为平稳可逆ARMA(p，q)模型的自回归系数多项式；θ(B)=1-θ1B-…-θqBq，为平稳可逆ARMA(p，q)模型的移动平滑系数多项式。

2.平稳性检验

由ARIMA模型原理可知，建模序列需是平稳序列，因此首先检验城镇居民可支配收入UIt序列和农村居民人均纯收入RIt序列的平稳性。根据UIt序列和RIt的时序图(见图1)，两个序列均有明显的增长趋势，因此大致可判断出原序列UIt和RIt均为非平稳时间序列，在建立模型之前需要对原序列进行平稳化处理。

为精确判断序列的平稳性并进行平稳化处理，运用Eviews9.0软件采用ADF单位根检验法进行进一步的检验和差分选择。[15](P175-184)由表1的检验结果可知，UIt序列ADF检验统计量值为2.3851，p值为0.9999，1%、5%、10%临界值分别为-3.6999、-2.9763、-2.6274，不能拒绝存在单位根的原假设，故UIt序列不平稳。所以对序列进行一阶差分得到△UIt序列，再对△UIt序列进行ADF检验，结果显示检验的p值为0.9453，不能拒绝存在单位根的原假设，即一阶差分序列不平稳。继续对△UIt序列作差分处理得到二阶差分序列△2UIt，再对△2UIt序列进行ADF检验，检验的P值=0.0005<0.01，拒绝原假设，因此二阶差分序列在1%的显著性水平下是平稳序列。

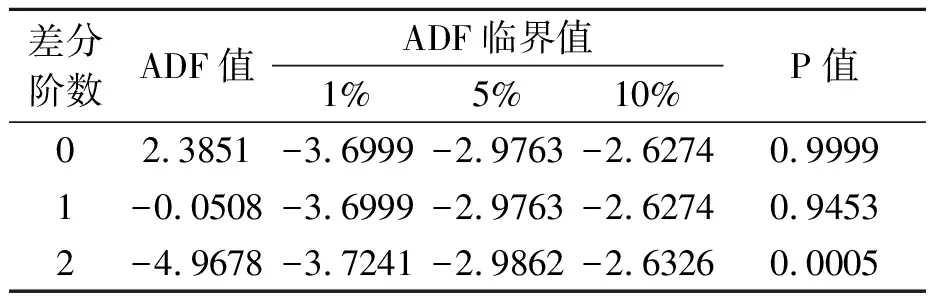
表1 UIt序列的ADF检验结果

同理，运用ADF单位根检验法对RIt序列进行平稳性检验，结果如表2所示，RIt序列和一阶差分序列△RIt为非平稳序列，二阶差分序列△2RIt在1%的显著性水平下是平稳序列。

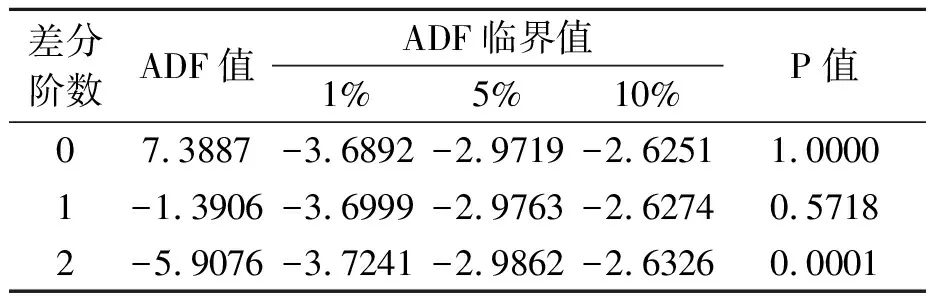
表2 RIt序列的ADF检验结果

3.模型识别

对城镇居民人均可支配收入UIt序列建立ARIMA(p，d，q)模型，由平稳性检验结果，UIt序列和一阶差分序列△UIt为非平稳序列，二阶差分序列△2UIt是平稳序列，因此d=2，再根据△2UIt序列自相关系数和偏自相关系数的性质判定模型的阶数p和q。

△2UIt序列自相关函数和偏自相关函数如图3所示。从图3可以看出，△2UIt序列的偏自相关系数在滞后2阶时表现出拖尾，而自相关系数在滞后5阶时落在了2倍标准差的边缘，从图3很难直观的确定模型中的两个参数，因此通过大量的试验和对比分析，根据AIC和SC越小越好的准则并观察模型参数的显著性，最终确定出来的相对最优模型为疏系数模型ARIMA(0，2，(1，2，5))。

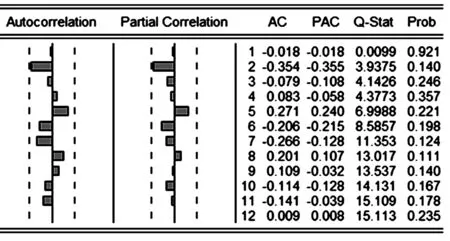
图3 △2UIt序列的自相关和偏自相关图

同理，对农村居民人均纯收入RIt序列建立ARIMA(p，d，q)模型，根据平稳性检验结果，ARIMA(p，d，q)模型中d=2。二阶差分序列△2RIt自相关函数和偏自相关函数如图4所示。

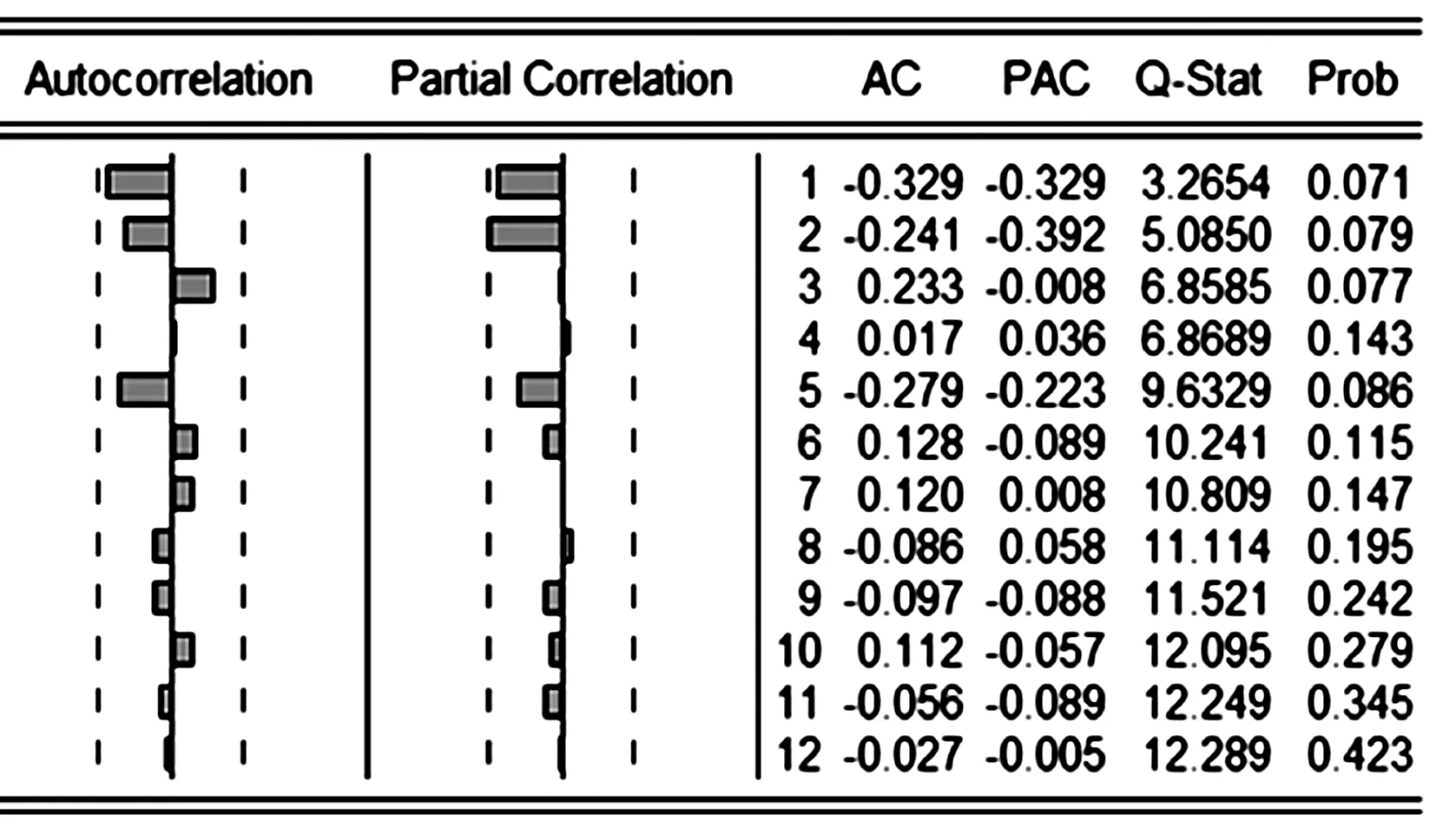
图4 △2RIt序列的自相关和偏自相关图

根据图4，△2RIt序列的自相关函数和偏自相关函数均表现出拖尾性质，经过反复试验和对比分析，最终确定的相对最优模型为ARIMA(0，2，2)。

4.模型参数估计和诊断

利用最小二乘估计法分别对UIt序列所建立的ARIMA(0，2，(1，2，5))模型和RIt序列所建立的ARIMA(0，2，2)模型进行参数估计。 ARIMA(0，2，(1，2，5))模型估计结果如下：

Δ2UIt=110.01+εt-0.28εt-1-0.69εt-2+0.59εt-5

(2)

t=(3.36) (-2.53) (-5.68) (12.80)

ARIMA(0,2,2)模型估计结果为：

Δ2RIt=53.92+εt-0.56εt-1-0.40εt-2

(3)

t=(5.05) (-2.94) (-2.10)

模型参数估计出来后，还需对模型的拟合效果进行检验，即对模型的残差序列进行白噪声检验。对UIt序列所建立的ARIMA(0，2，(1，2，5))模型的残差序列进行白噪声检验，残差序列滞后6阶、12阶的Q统计量的p值分别为0.557和0.876，均大于显著性水平0.05，不能拒绝原假设，即残差序列是白噪声序列，说明模型信息提取充分，拟合模型显著有效。

同理，对RIt序列所建立的ARIMA(0，2，2)模型的残差序列进行白噪声检验，结果表明：残差序列滞后6阶、12阶的Q统计量的p值分别为0.614和0.629，均大于显著性水平0.05，故残差序列是白噪声序列，数据信息已全部提取，拟合模型显著有效。

5.模型验证与预测

利用以上对UIt序列所建立的ARIMA(0，2，(1，2，5))模型和对RIt序列所建立的ARIMA(0，2，2)模型，对1991—2019年样本区间内城镇居民人均可支配收入和农村居民人均纯收入进行预测，然后再作差和作比，求出湖北省各年城乡居民收入绝对差距及收入比的预测值，并与实际数据进行比较，计算出两个值之间的相对误差。结果表明：整个样本区间内城乡收入绝对差距平均相对误差为5.13%，收入比平均相对误差为4.23%，预测精度较高，说明模型拟合效果较好。因此，利用拟合的模型对湖北省2020—2022年城乡居民收入绝对差距及收入比进行短期预测，预测结果见表3，其中样本区间内只列出了2016—2019年的预测结果。

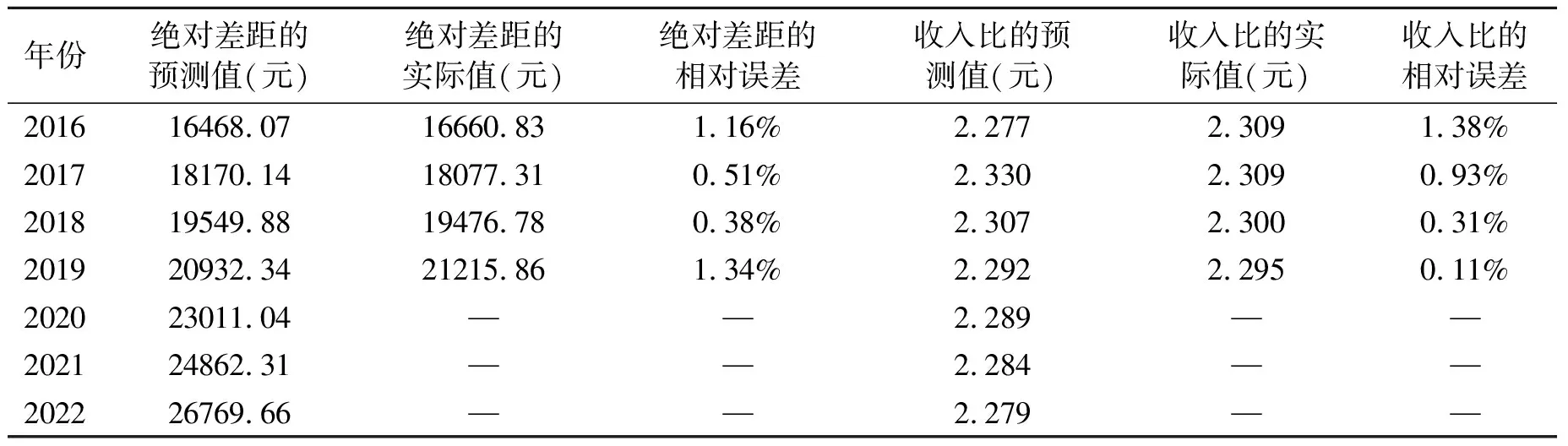
表3 城乡收入差距预测值与实际值的对比

从表3的预测结果可以看到，利用UIt序列所建立ARIMA(0，2，(1，2，5))模型和RIt序列所建立的ARIMA(0，2，2)模型可以对湖北省2020—2022年的城乡居民收入差距进行短期预测。2020年、2021年和2022年湖北省城乡居民收入绝对差距预测结果均大于2019年实际值且呈逐年扩大态势；收入比预测结果分别为2.289、2.284和2.279，相比2019年的实际值2.295略微有所下降趋势，但不明显，基本维持在2.28左右的水平，波动幅度较小。

三、结语

根据以上研究，运用ARIMA模型对湖北省城乡居民收入差距进行预测分析，预测值和实际值之间的平均误差百分比较小，表明模型预测精度较高，因此模型可用来对湖北省2020—2022年的城乡收入差距进行短期预测。预测结果表明：未来三年湖北省城乡居民收入绝对差距将进一步扩大，相对差距略微呈现下降趋势但下降幅度较小，城乡收入比相较于世界劳工组织公布的标准仍然偏高。可见，未来几年湖北省城乡居民收入差距悬殊问题虽略微有所改善但形式依然严峻，因此多渠道增加农村居民收入水平，及时有效扭转收入差距扩大态势，实现城乡经济更均衡平稳的发展是目前湖北省经济发展中亟待解决的重大问题之一。