超临界水对流换热的宽范围数据分析及换热关联式的建立

蔡文熠，匡　波

超临界水对流换热的宽范围数据分析及换热关联式的建立

蔡文熠，匡波

（上海交通大学，上海 200240）

由于超临界流体在拟临界区复杂的物性变化，其管内流动的对流换热模式与亚临界流体有很大不同。除实验研究和理论分析外，许多学者建立了用于预测换热系数的超临界流体换热关联式，但现有的关联式均不能在宽广的参数范围上取得满意的预测效果。因此，在建立了超临界水竖直上升流宽范围换热实验数据库的基础上，运用机器学习方法分析了影响换热的典型无量纲数与努塞尔数的关系，建立客观评价指标，选出适当的关联形式并建立新的换热关联式。换热关系的非线性分析结果表明，其非线性特征在密度比上的表现最为显著。结合非线性特征的趋势和客观评价指标的对比，在换热关联式中引入对数型的密度比项，由此提出宽范围的超临界水竖直上升流换热关联式，其在数据库上的预测表现明显优于现有关联式。

超临界水；换热关联式；宽范围换热实验数据库；机器学习

当压力高于临界压力时，流体会失去气相与液相的分界，这种单相状态被称为超临界。处于超临界状态的流体具有良好的传热和流动特性，在动力工程领域有广泛的应用前景。然而，在被称为拟临界区的温度范围内，超临界流体的物性会发生剧烈变化，传统的单相换热关联式无法准确预测其换热系数，这给超临界流体的工程应用带来很大困难。

根据现有研究，拟临界区的流体在径向和流向上易出现陡峭的密度梯度，从而引发浮力效应和加速效应，对换热强度产生复杂影响[1]。然而，对于这种影响关系的具体形式还未能给出准确的定量表述，学者们只能尝试在关联式中加入物性比、浮力因子、加速因子等修正项并用实验数据拟合出修正关联式。一方面大部分修正关联式都没有在较宽广的参数范围内（尤其是拟临界区）取得令人满意的效果，另一方面对于这些修正变量与换热强度的关系，少有学者利用数据科学的工具进行数据分析和讨论，以筛选出重要的修正变量及适合的关联形式。因此，需要在宽广参数覆盖范围的换热实验数据集上进行深入的数据分析，确定应引入关联的变量组合及恰当的关联形式，以获得更好的预测精度。

1　数据库建立及均衡化处理

本文针对超临界水管内竖直上升流的换热实验工况，从1963—2016年的文献[2-23]中共搜集到18 079个有效数据样本。样本包含管径、压力、质量流密度、热流密度、流体温度b或焓值b、壁面温度w这六项原始实验参数。

由于文献目的及获取途径的不同，原始样本数在各数据来源间差异很大（最大数据源数据量为5 088，最小源只有77）。样本量较大的数据源会使模型向它过度“偏移”，而样本量较小的数据源则容易被模型“忽视”，这对后续建模十分不利。

在样本量小的数据源上随机选取样本视为新样本加入数据库，以平衡数据分布，这种方法称为随机过采样。本文中当某数据源样本量小于最大数据源的四分之一时，需要对该数据源进行一定比例的过采样，且最大采样倍数不超过10。经随机过采样后，得到规模为26 358的均衡化数据集，后续的建模和评价都将在均衡化数据集上进行。

2　无量纲自变量的筛选

前人基于假设、理论推导或实验拟合，得到了许多不同类型的无量纲数作为修正因子引入换热关联式中，主要包括反映物性变化的因子、反映浮力效应的因子以及反映热加速效应的因子。一方面，由于关联式表现不佳，更多变量被引入试图反映出不同因素对换热的影响；另一方面，过多的变量容易导致关联式系数不稳定，模型失真，外推能力变差。这就需要对自变量作得当的筛选，以选取尽可能少但又能充分反映换热关系特点的自变量。

参考不同学者提出的换热关联式及其中因子，挑选出以下9个相对较多学者使用的无量纲数作为待筛自变量（见表1）。

表1　选取的待筛选自变量

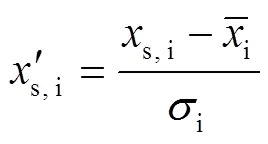
最终模型是否包含这些变量，还需要结合数据进行筛选。自变量筛选需要考虑两方面因素：

（1）该变量对于影响程度的大小，即变量与的关联度；

（2）变量之间是否存在相关性，内部相关性强的变量组将使模型参数估计值不稳定，影响预测效果。

用Lasso回归方法可以筛去与目标函数关联度较低的变量并保留内部相关性弱的变量组[24]。Lasso线性回归模型的损失函数如下：

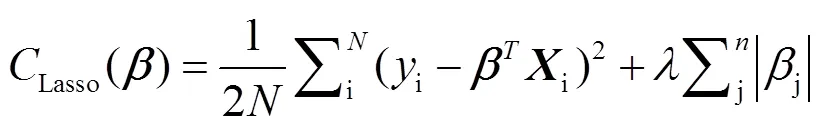
表2　各变量在Lasso回归中的系数估计值

r、r、+、*这4个变量因与模型关联度不显著或与保留变量组有较强相关性而被剔除，、、r、p,r、B这5个自变量被保留。

3　换热关系中的非线性成分分析

3.1　线性模型的评价

使用Lasso回归保留下来的自变量组及相应系数建立线性模型，并引入下列指标来评价模型预测效果：

其中为平均相对误差，2为决定系数。另外，还定义10、20、30分别表示相对误差在10%、20%、30%以下的数据比例。在评价中采用交叉验证的思想，随机选取均衡化数据集中的70%样本作为训练集，余下的30%作为测试集，模型在训练集上得到其参数，并在测试集上评估效果。这样确保建立好的模型从未“见过”评价它所用的样本，有效防止过拟合的模型获得较高评价。

线性模型的评价指标如表3所示，其在测试集上的详细表现如图1所示。经过变量筛选后的线性模型已经能在一定程度上预测，但从图中看，仍有较多样本的预测相对误差超过30%，且一些样本的误差非常大。这说明线性模型不能较充分地表示换热关系。

表3　Lasso线性回归模型的评价

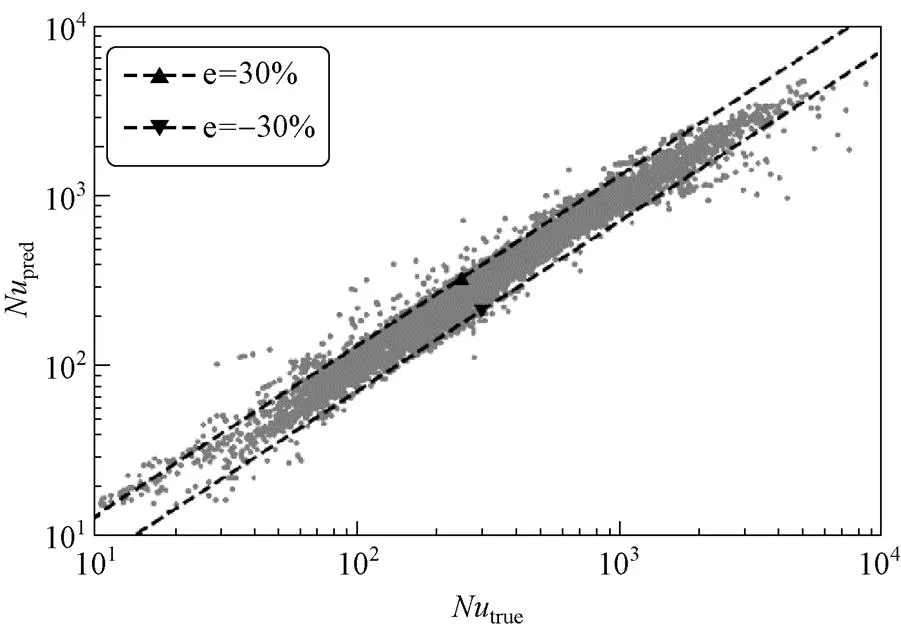
图1　Lasso线性回归模型的预测效果

3.2　非线性成分说明和验证

为进一步分析各变量在不同参数子空间上对换热关系的影响，根据超临界流体的物性状态把超临界流动工况分为三个不同温区，分别是拟临界温度附近、物性变化剧烈的拟临界区，温度远高于拟临界温度的拟气体区，以及温度远低于拟临界温度的拟液体区。Zahlan[25]用以下准则划分这三个区域：

其中临界压力c=22.064 MPa，拟临界温度pc单位为。

标准回归系数SRC（Standard Regression Coefficient）是标准化后的自变量与目标函数的线性回归系数，其相对大小反映了自变量与因变量之间关联关系的强弱。不同物性状态分区中自变量与的SRC如图2所示。可以看到，不同分区的SRC差异较大，尤其是r、B在不同区域有数倍的差异。由于线性回归系数可以看做是一个复杂关系在一定范围内一阶偏导数的期望值，因此，本文认为无量纲数与换热强度的关系可能由某个复杂的非线性关系所表达，而这一非线性关系的一阶偏导数平均值在各物性状态分区内并不相同，这就形成图2中的分区表现。

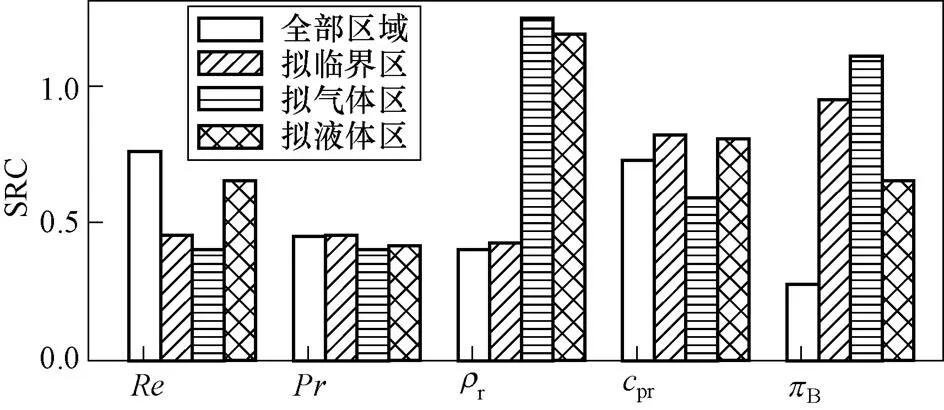
图2　不同物性状态分区各变量SRC

为验证换热系数与自变量组的非线性关系，引入核岭回归法。岭回归法相对Lasso回归改用用了模型系数的2-范数作惩罚，约束了变量间的共线性对模型系数的影响：

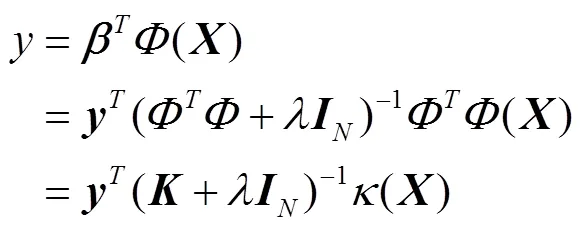
表4　本文选取的常用核函数

表5　各核函数所建立模型的评价

3.3　非线性关系的变量间比较分析

定义Lasso模型的残差为：

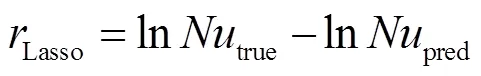
决策树逐级生成判断条件，以条件的“是”和“否”将变量空间不断二分，最终把变量空间划分为若干个对应着不同输出结果的子空间，每个判断条件应使得当前层级上“是”空间和“否”空间的信息增益（即信息熵在空间二分后的熵减，本问题中使用绝对误差衡量信息熵）最大化：

决策树较易陷入过拟合，随机森林通过引入随机性构造多颗不同的决策树并输出各决策树平均结果改进了模型的泛化性能，更适合于实际工程应用。随机森林模型中，可以根据变量带来的信息增益之和来衡量变量对于目标问题的重要度：

表6　不同树深度下的变量重要度

4　换热关联式的建立

4.1　非线性关联形式探究

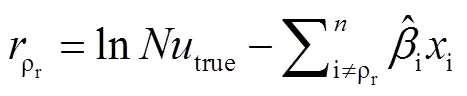
在引入后计算公式（12），可以把非线性关系更“集中”到密度比这一变量上。画出各数据样本上与之间的趋势如图3所示。

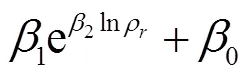
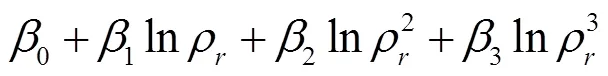
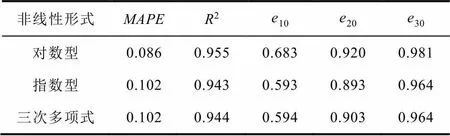
表7　猜想非线性形式的评价

显然对数型的非线性模型效果最优，于是把对数型的非线性模型写成公式（16）。值得一提的是，此时给出的最终公式（16）是对数型非线性模型在整个均衡化数据集上优化的结果，而非训练集。

根据本文数据库的覆盖范围，公式（16）的推荐使用范围为：=0.006～0.038 m，=22.4～31.03 MPa，=200～3 500 kg/m2·s，=37～2 000 kW/m2，b=256～2 968 kJ/kg。

4.2　关联式评价

用得出的关联式对本文数据库中的样本进行预测，效果如图4所示。

图4　新关联式的预测效果

本文挑选了9个现有关联式与本文关联式进行对比，包括早期研究中评价较好的Yamagata、Watts的关联式，以及7个在大规模数据集上得到的宽范围关联式，计算这些关联式的5项评价指标、2、10、20、30，见表8。前文关联式中Jackson，Mokry，刘鑫，Yu的关联式效果相对较好；而本文关联式的相比其余中最好的Mokry关联式还下降了近一半，2达到0.9以上，并且在各个误差带内都显示出了明显的优势。

表8　本文关联式和其他关联式的评价对比

进一步地，针对超临界流动传热较难预测的拟临界区传热强化和传热恶化两类典型特征，本文挑选了Lei[11]的传热强化和传热恶化实验数据各一组，展示现有关联式和本文关联式在该区域内对的预测能力，如图5和图6所示。样例实验的不确定度如表9所示。可以看出本文提出的关联式在全范围内能够较为紧密地跟随传热强度的突升和突降趋势。

图5　不同关联式对传热强化数据预测能力的比较

图6　不同关联式对传热恶化数据预测能力的比较

表9　样例实验的不确定度

5　结论

本文在搜集、整理并建立超临界水竖直管内上升流换热实验数据库的基础上，运用机器学习方法进行数据分析，并得到以下结论：

（2）通过密度比非线性成分的趋势分析和客观评价指标的比较，建立了基于对数型密度比项的超临界水换热关联式，新关联式的预测结果与数据库的实验数据符合较好；较以往此类关联式，新关联式预测能力有较大提升，尤其在以往预测效果不佳的拟临界区。

［1］ Jackson J D．Models of heat transfer to fluids at supercritical pressure with influences of buoyancy and acceleration［J］．Applied Thermal Engineering，2017，124：1481-1491．

［2］ Swenson H S，Carver J R，Kakarala C R．Heat Transfer to Supercritical Water in Smooth-Bore Tubes［J］．Journal of Heat Transfer，1965，87（4）：477-483．

［3］ Vikhrev Y V，Barulin Y D，Kon’Kov A S．A study of heat transfer in vertical tubes at supercritical pressures［J］．Thermal Engineering，1967，14（9）：116-119．

［4］ Ackerman，J．W．Pseudoboiling Heat Transfer to Supercritical Pressure Water in Smooth and Ribbed Tubes［J］．Journal of Heat Transfer，1970，92（3）：490．

［5］ Yamagata K，Nishikawa K，Hasegawa S，et al．Forced convective heat transfer to supercritical water flowing in tubes［J］．International journal of heat and mass transfer，1972，15（12）：2575-2593．

［6］ Griem H．A new procedure for the prediction of forced convection heat transfer at near-and supercritical pressure［J］．Heat and Mass Transfer，1996，31（5）：301-305．

［7］ Mokry S，Pioro I，Kirillov P，et al．Supercritical-water heat transfer in a vertical bare tube［J］．Nuclear Engineering & Design，2010，240（3）：568-576．

［8］ 胡志宏．超临界和近临界压力区垂直上升及倾斜管传热特性研究［D］．西安：西安交通大学，2001．

［9］ 徐峰，郭烈锦，毛宇飞，等．超临界压力下水在垂直加热管内传热特性的实验研究［J］．西安交通大学学报，2005，39（5）：468-471．

［10］黄志刚，李永亮，曾小康，等．竖直圆管通道内超临界水传热实验及数值模拟研究［J］．原子能科学技术，2012（07）：35-39．

［11］ Lei X，Li H，Zhang W，et al．Experimental study on the difference of heat transfer characteristics between vertical and horizontal flows of supercritical pressure water［J］．Applied Thermal Engineering，2017，113：609-620．

［12］ Zhang G，Zhang H，Gu H，et al．Experimental and numerical investigation of turbulent convective heat transfer deterioration of supercritical water in vertical tube［J］．Nuclear engineering and design，2012，248：226-237．

［13］王飞，杨珏，顾汉洋，等．垂直管内超临界水传热实验研究［J］．原子能科学技术，2013，47（6）：933-939．

［14］潘杰，杨冬，董自春，等．垂直上升光管内超临界水的传热特性试验研究［J］．核动力工程，2011，32（1）：75-80．

［15］赵萌．典型流道内超临界水流动传热实验和数值模拟研究［D］．上海交通大学，2017．

［16］王磊．垂直圆管内超临界水的传热特性研究［D］．上海：上海交通大学，2012．

［17］张思宇，陈佳跃，赵萌，等．超临界压力下竖直圆管内不同流体的传热特性［J］．原子能科学技术，2016，50（8）：1395-1401．

［18］ Jackson J D，Cotton M A，Axcell B P．Studies of mixed convection in vertical tubes［J］．International Journal of Heat & Fluid Flow，1989，10（1）：2-15．

［19］ Shitsman M E．Temperature conditions in tubes at supercritical pressures［J］．Teploenergetika，1968，15（5）：72-77．

［20］ Herkenrath H，Mörk-Mörkenstein P，Jung U，et al. Wärmeübergang an Wasserbei Erzwungener Strömungim Druckbereichvon 140 bis 250 bar［J］．EURATOM，EUR，3658．

［21］ Alferov N S，Rybin R A，Balunov B F．Heat transfer with turbulent water flow in a vertical tube under conditions of appreciable influence of free convection［J］．Thermal Engineering，1969，16（12）：90-&．

［22］ Lee R A，Haller K H．Supercritical water heat transfer developments and applications［C］//International Heat Transfer Conference Digital Library．Begel House Inc.，1974．

［23］王大荣，张忠占．线性回归模型中变量选择方法综述［J］．数理统计与管理，2010（04）：615-627．

［24］ Zahlan H，Tavoularis S，Groeneveld D C．A look-up table for trans-critical heat transfer in water-cooled tubes［J］. Nuclear Engineering and Design，2015，285：109-125．

［25］唐亘．精通数据科学：从线性回归到深度学习［M］．北京：人民邮电出版社，2018：227-241．

［26］ Watts M J，Chou C T．Mixed convection heat transfer to supercritical pressure water［C］//International Heat Transfer Conference Digital Library．Begel House Inc.，1982．

［27］ Cheng X，Yang Y H，Huang S F．A simplified method for heat transfer prediction of supercritical fluids in circular tubes［J］．Annals of Nuclear Energy，2009，36（8）：1120-1128．

［28］刘鑫，匡波．竖直上升管中超临界水的宽范围换热关联式［J］．核科学与工程，2012，32（4）：344-353．

［29］ Yu J，Jia B，Wu D，et al．Optimization of heat transfer coefficient correlation at supercritical pressure using genetic algorithms［J］．Heat and Mass Transfer，2009，45（6）：757-766．

［30］文青龙，王弘扬，赵萌，等．垂直圆管内超临界水传热关联式研究［J］．核动力工程，2017，38（2）：15-18．

Wide-range Data Analysis of Supercritical Water Convection Heat Transfer and Establishment of Heat Transfer Correlation

CAI Wenyi，KUANG Bo

（Shanghai Jiao Tong University，Shanghai 200240，China）

Due to the complex physical property changes of supercritical fluid in the pseudo-critical region，the convective heat transfer mode of the tube flow is very different from that of subcritical fluid．In addition to experimental research and theoretical analysis，many scholars have established supercritical fluid heat transfer correlation for the prediction of heat transfer coefficient，but none of the existing correlation can achieve satisfactory prediction results over a wide range of parameters．Therefore，based on the established heat transfer experiment database of the vertical upflow of supercritical water，the machine learning methods are used to analyze the relationship between the typical dimensionless numbers that have impact on heat transfer and the Nusselt number．According to objective evaluation indicators，appropriate correlated form is selected and a new heat transfer correlation is established．The results of non-linear analysis of heat transfer relationship show that this nonlinearity is most pronounced in the density ratio．Combining the trend of the non-linear characteristics and the evaluation results of objective indicators，the logarithmic density ratio term is introduced into the heat transfer correlation，thereby a wide-range heat transfer correlation of the vertical upflow of supercritical water is established and its prediction performance on the database is much better than existing correlations．

Supercritical water；Heat transfer correlation；Wide-range heat transfer experiment database；Machine learning

TK124

A

0258-0918（2021）03-0471-08

2020-07-21

蔡文熠（1995—），男，福建三明人，硕士研究生，现主要从事反应堆热工方面研究