基于全速度差模型的城市快速路合流区交通流特性研究

郭海兵，曲大义，洪家乐，赵梓旭

(青岛理工大学 机械与汽车工程学院，青岛 266525)

城市快速路是城市交通的动脉，建设布局加快了城市发展速度，但随着车辆需求不断增长，快速路的畅通受到影响和挑战，特别是早晚高峰时段，在快速路合流区、分流区及交织区经常出现拥堵现象，形成了常发性瓶颈路段，存在诱发交通流失效问题等隐患。研究城市快速路常发性瓶颈路段交通流特性，深入分析交通拥堵产生机理，对于制定瓶颈路段交通管理措施、有效缓解交通拥堵具有十分重要的意义和价值。

国内外学者对此展开的研究主要有：CASSIDY等[1]认为快速路合流区汇入段上游路肩车道交通流密度增大到一定值后，车辆向快速路车道换道行为增多，引发交通流崩溃及通行能力下降问题，并且换道行为是引发拥堵和流出率下降的主要原因；JIAN等[2]利用上海市快速路数据研究交通流失效问题，利用换道数据研究分析了合流区道路交通流的早发性失效问题；WANG等[3]通过实证研究认为换道行为对交通流的影响表现为换道打破了与跟驰车辆间的平衡状态，从破坏到恢复的持续时间为25 s；LAVAL等[4]建立了粒子运动模型，描述车辆换道后对目标车道后随车的影响；KESTING等[5]用跟驰模型的加速度函数进行换道行为激励和安全约束，实现以较少的参数确保模型的精准度，使换道模型与跟驰模型集成；杨小宝[6]提出了考虑换道实施过程模型，定量分析换道行为对交通流的影响；何梦辰[7]研究后认为换道行为是导致合流区交通流从稳定状态向不稳定状态转变的重要影响因素，应用突变理论推导车队在瓶颈处速度变化非连续性；郭涛[8]应用流量、速度和密集度研究快速路合流区交通流时空变化特性，认为合流区车辆间由于存在着复杂的交互跟驰与强制换道行为，匝道车辆汇入行为对处于同步流状态的主线交通流造成干扰，其中对外侧路肩车道交通流的干扰最严重。

本文研究合流区交通流特性主要侧重于研究合流区车辆强制换道对主线交通流的影响，在这种环境下主线交通流由饱和流向拥挤流过渡，匝道车辆为达到换道目的强制向主线车道并线，必然对主线上游车辆正常行驶产生不利影响。考虑合流区车辆并入主线换道行为是一个跟驰和换道综合驾驶过程，利用全速度差模型[9](FVDM：Full Velocity Difference Model)描述主线后随车与完成强制换道前车的跟驰行为特性，并运用数值仿真方法，构建快速路合流区交通环境，模拟从车辆换道进入目标车道时刻开始，目标车道交通流拥堵形成及消散过程，使用速度、车头间距及位移指标分析合流区交通流特性，揭示合流区常发性瓶颈路段交通拥堵产生及消散机理。

1 城市快速路合流区交通流特性

快速路合流区车辆换道行为包括自由换道、协作换道和强制换道，自由换道指主线车道车流处于自由流速度状态，车辆换道不受主线车道车辆影响；协作换道指主线后随车与换道车辆之间距离在现有行驶状态下将会在合流区发生冲突，换道车辆发出换道请求后，后随车为避免冲突发生，预先采取减速或换道方式协助其完成换道；强制换道指主线车道车辆密度较大，道路使用空间压力增大，同时汇入车辆在加速车道面临行驶空间狭小，不断减速并迫于停车压力强制并入主线车道的行为。以上换道行为中协作换道和强制换道均会使当前车道上游及目标车道上游交通流受到扰动，其中强制换道由于换道车辆的强行并线，主线车道后随车被迫采取紧急制动减速，导致其上游车辆相继减速，上游交通拥挤严重时容易引发交通流失效，极有可能诱发道路交通事故。合流区换道车辆与主线车道的车辆交互行为如图1所示。

图1 城市快速路合流区瓶颈路段车辆交互行为示意

2 合流区交通流全速度差模型

城市快速路合流区换道行为实质是一个跟驰与换道综合驾驶过程，换道行为对目标车道上游车辆产生的影响具体表现为：换道过程中车辆减速后，导致后随车及其上游车辆陆续减速，形成减速波向上游蔓延，引发上游车道交通流扰动，当车流密度超过饱和密度后往往容易引发交通流失效现象。根据以上分析，基于全速度差模型描述主线后随车与完成强制换道前车的跟驰行为特性，FVDM模型公式为

a(t)=κ[V(Δx(t))-v(t)]+λ·Δv(t)

(1)

式中：a(t)为t时刻目标车道后随车加速度；κ，λ为驾驶员速度敏感系数；Δx(t)为前后相邻车头间距；V(Δx(t))为最优速度函数；v(t)为t时刻后随车速度；Δv(t)为t时刻换道车辆与目标车道后随车速度差。

最优速度函数定义为

(2)

式中：V0为后随车期望速度；ln-1为换道车辆长度；b,β为常量参数。

本文利用NGSIM数据对模型参数完成标定，并分析换道行为对目标车道后随车影响。

3 模型参数标定

选定NGSIM实测数据集US101道路7：50—8：05时段数据进行模型参数标定。

3.1 数据筛选

为保证参数标定后模型具有理想的预测精度和泛化能力，首先按照以下条件筛选数据：

1) 研究涉及的相关车辆均为小汽车，换道车辆为上匝道后向主线路肩车道并线车辆，道路交通流密度为非自由流密度条件，主线后随车与换道车辆保持跟驰车间距≤50 m。

2) 由于跟驰过程中后随车加速度与前后车相对速度具有正相关性，根据GAZIS等研究[10]，筛选出皮尔逊相关系数值较大的10组样本。皮尔逊相关系数如式(3)所示：

(3)

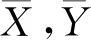
3) 车辆换道进入目标车道后，选择后随车连续稳定跟驰行驶时间在20 s以上作为样本数据。

根据以上条件筛选出样本数据10组共计6704条，数据精度为0.1 s。

3.2 参数标定

匝道车辆从进入目标车道后开始，筛选出换道车辆与后随车的行驶数据，并根据式(1)、式(2)计算后随车在各时间段行驶轨迹，计算模型输出值与观测值间的误差指标，误差指标中含有模型参数值，计算误差指标最小值时对应的模型参数值即为确立的最终标定模型参数值。

选用计量经济学中Theil不等式系数进行性能指标误差评价[11]，Theil函数式如下：

(4)

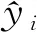
应用Matlab中optimtool遗传算法工具箱求解Theil优化函数最小值[12]，每次标定重复10次，选取误差最小值作为参数最终标定结果。算法参数设置为：初始种群数量500，最大进化代数300，交叉概率0.8，变异概率0.2，初始惩罚因子10，收敛容许误差10-6，停滞代数100。

观测数据中每一时刻的行驶轨迹取决于上一时刻的行驶轨迹，因此产生的误差将不断积累，为真实反映累计误差对误差评价的影响，基于跟驰全过程进行参数标定和验证，即目标车道后车在跟驰过程中每一时刻的行驶轨迹均根据前车各个时刻的实测数据和后车初始时刻的实测数据进行推导，推导中采用牛顿运动学速度、位移公式：

v(t+Δt)=v(t)+a(t)×Δt

(5)

(6)

式中：Δt为时间步长。

选择车头间距指标进行误差评价，将筛选的10组数据分别代入式(4)中，利用遗传算法工具箱函数求出标定参数，参数范围参照文献[13]确定，模型标定情况见表1。

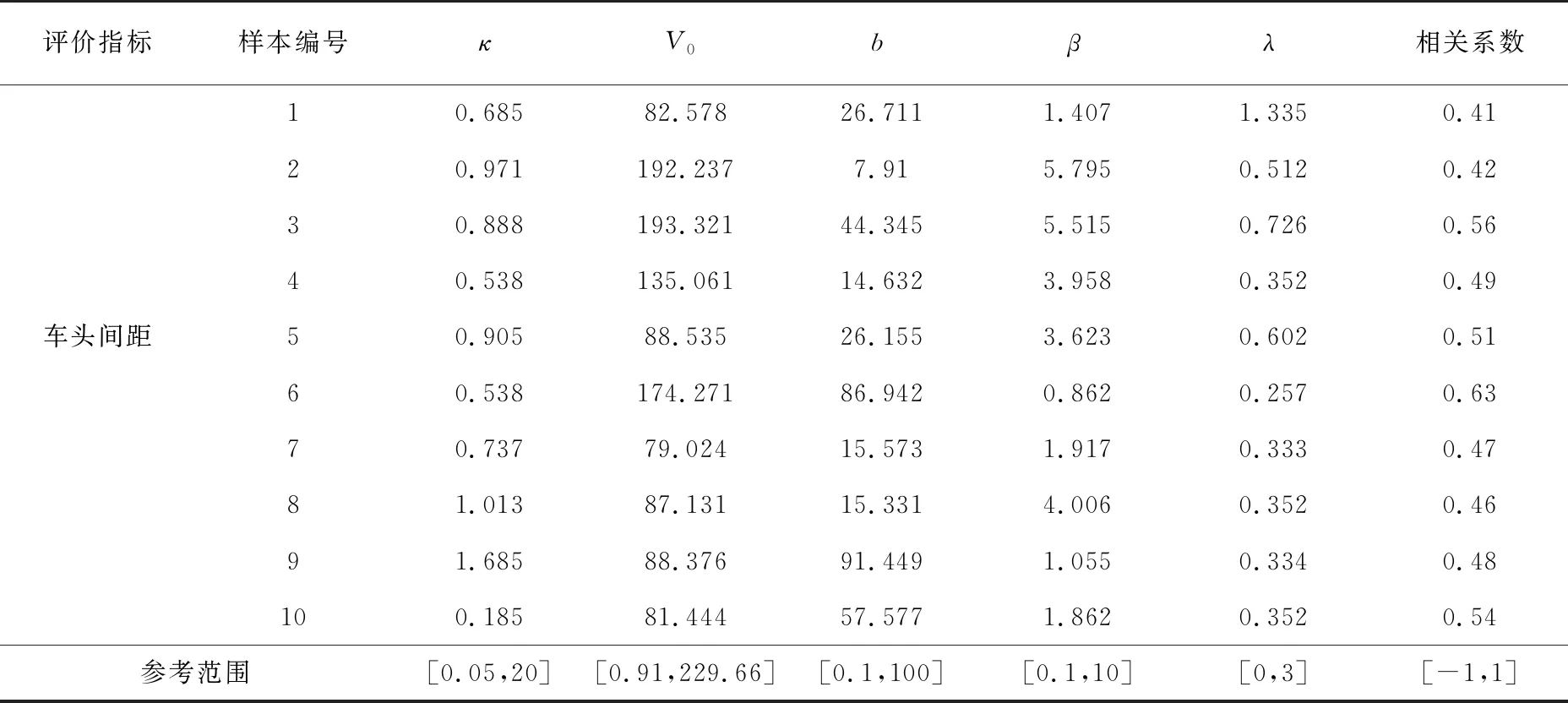
表1 模型参数标定结果

4 模型有效性验证

根据模型标定方法计算出待定参数，由测试数据中的前车行驶轨迹和后车初始轨迹仿真计算出后车全过程行驶轨迹，比较仿真轨迹与实测轨迹，通过相关误差指标进行模型有效性评价验证。最优参数选定过程为：①确立样本组1为训练集，其他9组样本为测试集，分别得到加速度、速度、车头间距、位移数据仿真值各9组；②确立样本组2为训练集，其他9组样本为测试集；③通过依次循环迭代10次得到仿真数据共计4×90组；④综合计算速度、车头间距、位移参数误差指标，选取误差值最小时的标定参数值作为模型最终标定参数值。

4.1 模型评价

考虑均方根误差具有反映数据偏离真实值大小程度的特点，确立均方根误差ERMS作为验证模型参数有效性指标：

(7)

建立均方根误差评价函数模型，根据文献[12],由于加速度指标敏感性高、不稳定，不易作为误差评价指标，以速度、车头间距和位移为误差评价指标，为消除指标间量纲的影响，采用min-max离散标准化方法进行数据归一化。

(8)

建立误差评价函数式E：

(9)

式中：v为后车速度；Δx为前后车的车头间距；d为后车位移。

具体过程为：每组样本作为训练集，其他9组作为测试集，循环运算10次，每次循环运算得到9组估计值，分别与实测值对应，计算9组测试样本的均方根误差并取平均值，分别求出速度、车头间距、位移的均方根误差归一化值。按照式(9)建立的误差评价模型，计算出每次循环计算得到的均方根误差归一化值，选取最小值作为最优参数值。每次循环计算得到的评价指标均方根误差归一化值见表2。

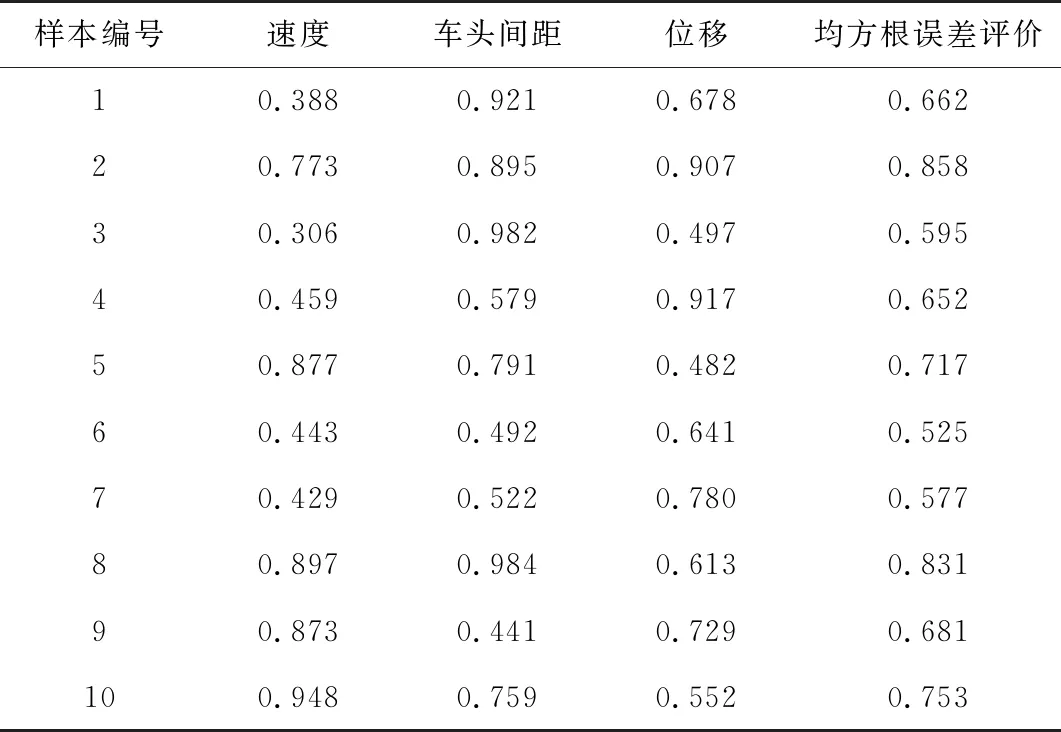
表2 均方根误差归一化值

由表2可知，样本组6作为训练集得到的均方根误差最小，选取样本组6标定参数为模型标定最优参数值。样本组6对应其他9组测试集，从中随机选择样本组8数据，对比样本观测值与模型仿真值误差关系，见图2。

样本组8的速度指标模型仿真值与观测值的均方根误差为2.067 m/s，车头间距指标的均方根误差为3.642 m，位移指标的均方根误差为4.387 m。从图2中看出，速度和车头间距的模型输出值在初始时段误差较大，原因可能是受驾驶员驾驶风格影响，跟驰后随车驾驶员驾驶风格较为激进，前方换道车辆进入目标车道后，仍保持与前车车辆较小的车头间距行驶；行驶轨迹由于受上一时刻位置的影响，在行驶过程中产生的误差不断累积，行驶位移在后期出现较大误差，但模型输出值总体上与实测数据走向吻合，说明模型能够较好地模拟车辆行驶轨迹。

4.2 模型仿真验证

为进一步研究分析快速路合流区换道行为对主线车道交通流影响，现设计数值仿真实验如下：设置一条长度为1200 m的单车道闭环道路，模拟合流区瓶颈路段，路段分布80辆车，车身长度均为5 m，整个实验过程包括换道后拥堵形成及拥堵消散2个阶段。

4.2.1 车队拥堵流形成阶段

车队头车设置为换道车辆，加速度为模型加速度值的1/2，速度为2.3 m/s，其他车辆初始速度设置为4.6 m/s，车辆初始时刻位置为

(10)

由于仿真步长0.1 s，时间间隔小，车辆速度更新按式(5)运算，车辆位置、车头间距更新可以近似按式(10)、式(11)仿真运算：

(11)

sn(t+Δt)=x(n-1)(t+Δt)-xn(t+Δt)

(12)

仿真运行时间为2000 s，仿真结果见图3。

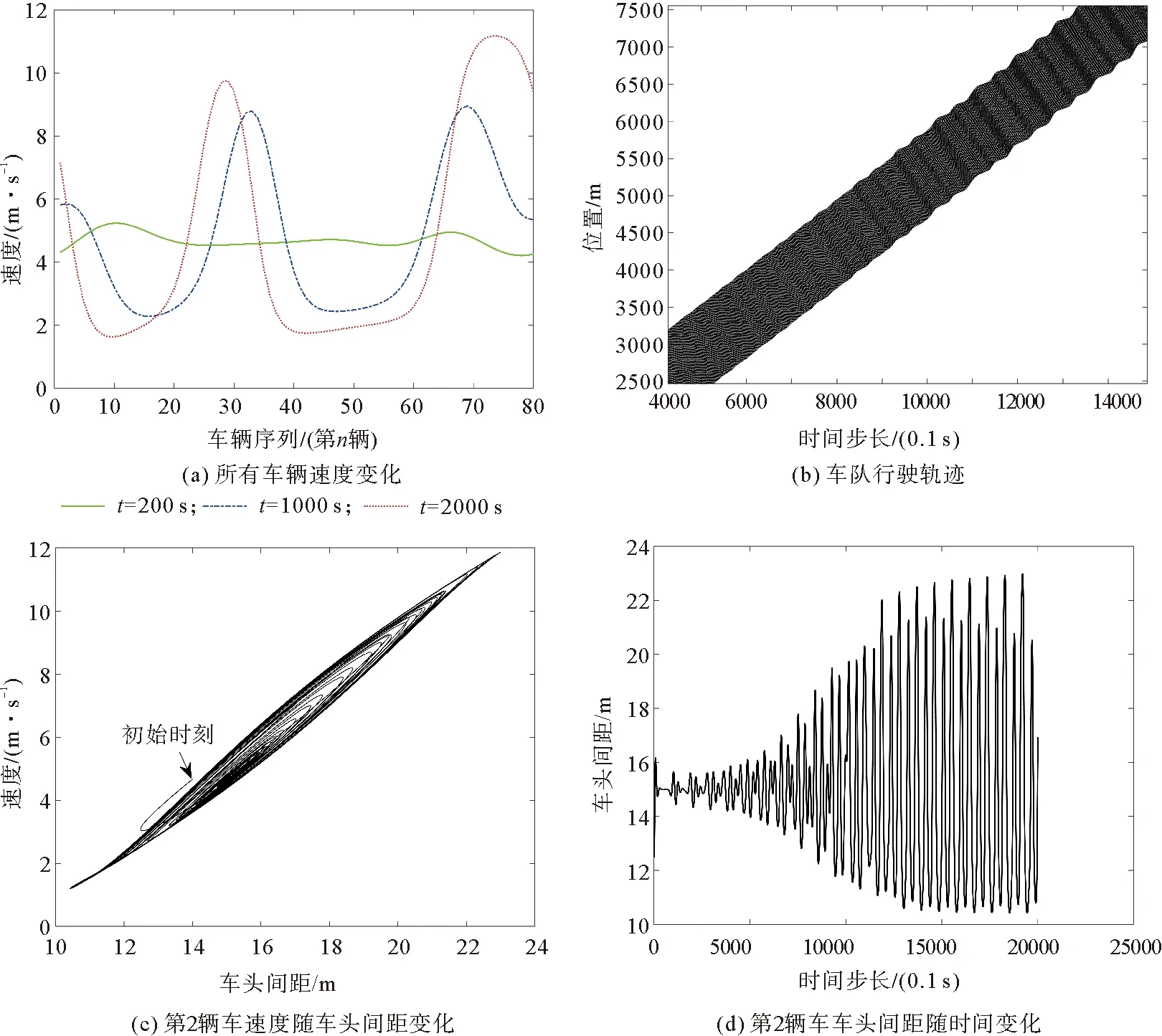
图3 车队交通拥堵流形成阶段

图3(a)分别提取200，1000，2000 s 3个时刻所有车辆的速度值，可以看出匝道车辆进入主线车道初始阶段，主线车道上游车辆在初始时段内彼此间能够保持既有速度和车间距离，速度波动较小，行驶状态比较稳定；车辆换道后由于没有及时调整速度和加速度，打破了上游车道车辆间的行驶平衡状态：首先后方紧随车辆在车头间距变小情况下，为自身安全考虑采取了制动减速行为，导致上游车辆相继采取减速措施，形成减速波向上游传播，导致出现交通流振荡，并且随着时间推移车辆间速度差越来越大，交通流振荡现象愈加剧烈，在2000 s时刻部分车辆速度值接近0，拥堵现象严重，交通流接近失效。图3(b)为车队所有车辆的行驶轨迹，在最初600 s时间内所有车辆行驶轨迹比较平稳，从600 s开始车队出现扰动，车辆由前至后相继减速随后依次加速，从900 s开始交通流振荡现象表现显著，并且随着时间推移交通流的振荡幅度在不断加大。图3(c)为车队第2辆车的速度与头车车头间距变化关系，由图可以看出车头间距与速度呈现环形线圈式振荡变化，在初始时间内环形线圈变化幅度小，表明第2辆车与头车车头间距及速度变化范围小，行驶状态较稳定；随着时间推移，环形线圈内径不断增大，在仿真终了时刻内径最大，此时出现车头间距与速度的两个极端值分别为：车头间距最大值22.97 m、车辆速度最大值11.85 m/s，车头间距最小值10.46 m、速度最小值1.209 m/s，表明此时第2辆车处于急加速与急减速的行驶状态，反映出整个车队拥堵状态比较严重，交通流接近失效。图3(d)为第2辆车在仿真时间内与前车车头间距随时间变化情况，验证了对图3(c)的结论分析。

4.2.2 车队拥堵流消散阶段

仿真设置车队头车仍为换道车辆，各车辆初始位置、初始时刻速度及与前车的车头间距设置与上一仿真时段2000 s时刻设置相同，头车加速度增加至2倍，模拟换道车辆开始加速行驶；其他车辆速度、车头间距、行驶位移计算规则不变，仿真运行600 s，并分别提取30，200，600 s时刻所有车辆行驶速度、行驶轨迹及第2辆车速度、车头间距变化情况见图4。

图4 车队交通拥堵流消散阶段

从图4(a)可以看出在初始时刻所有车辆间速度差距较大，在30 s时刻最大速度达到8.8 m/s，最小速度为2.3 m/s；随着时间推移，在600 s时刻所有车辆速度均在4.7 m/s左右，说明此时所有车辆基本保持相同速度匀速行驶，交通流恢复到稳定平衡状态。图4(b)为所有车辆随时间行驶轨迹，可以看出随着时间推移，车队速度波动逐渐减弱，大约在300 s以后车队所有车辆处于匀速稳定行驶状态。图4(c)为第2辆车速度随与前向车头间距变化关系，由图可以看出在初始时间阶段，第2辆车与其前车车头间距及自身速度变化幅度最大，出现了车头间距、速度的两个极端值分别为：车头间距最大值21.84 m、速度值11.20 m/s，车头间距最小值12.52 m、速度值2.516 m/s，说明第2辆车在初始时段内速度受车头间距影响不稳定，车辆处于振荡行驶状态，随着时间推移其车头间距振荡环内径不断减少最终消失，表明车辆最终达到稳定行驶状态。图4(d)为第2辆车车头间距随时间变化情况，变化范围验证了对图4(c)的分析。

5 结论

本文以城市快速路合流区为研究场景，研究匝道车辆换道行为对目标车道上游交通流扰动影响，在全速度差跟驰模型(FVDM)基础上，分析主线后随车与换道前车的跟驰行为特性，利用NGSIM数据使用遗传算法进行模型参数标定，并通过对比分析样本观测值与模型输出值误差，验证了标定后的模型能够较好地模拟车辆行驶轨迹；最后设计数值仿真实验，模拟合流区换道导致的拥堵流形成及消散过程。

合流区换道行为对主线上游车道交通流扰动影响机理为：合流区达到饱和流量后，主线道路空间资源减少，匝道车辆强制换道导致出现换道车辆与主线上游车道后随车的博弈，这种博弈行为程度越激烈，换道车辆速度越小，完成换道所需时间就会越长，从而给上游车道车辆带来的延误时间越长，由此引发交通流失效的风险越高；车辆换道后只有及时采取加速措施，拥堵流才会尽快消散。

通过研究分析进一步证明合流区匝道车辆换道行为是导致瓶颈路段交通流失效的主要原因，研究可为加强快速路合流区常发性瓶颈路段交通安全管控、缓解交通拥堵问题提供理论参考。此次研究过程中理论分析及仿真实验设计过程中主要考虑主线路肩单车道交通环境，假设车辆均为小汽车，条件理想化，与实际复杂道路场景存在一定差距。随着智能网联和自动驾驶技术的发展，城市道路上将会出现无人驾驶车辆与有人驾驶车辆混合行驶现象，在城市快速路路段如何实现无人驾驶车辆与有人驾驶车辆间协同并保证行车安全是下一步的研究方向。