基于ABAQUS软件的海底电缆反应力锥切削仿真及切削参数优化

曲爱涛， 高常青， 余 超， 吴绍聪， 杨 波

(济南大学 机械工程学院， 山东 济南 250022)

反应力锥的切削是大长度海底电缆在制作软接头时的重要工序， 具体操作是将绝缘层切削成锥状， 预留足够长度的铜导线。 目前反应力锥主要依靠人工进行切削， 随着海底电缆等级的提高， 截面绝缘层加厚， 人工切削效率低下。 为了提高切削效率， 相关切削设备逐渐涌现。 赵谦益[1]研究了双刀切削绝缘锥套的加工方式， 在加工绝缘锥套时， 先对锥面进行粗车，然后采取双刀对称的方式细车；该方式能够解决单面切削时因受切削力影响而造成锥套变形的问题，但是车刀的材料去除效率较低，不适用于大截面反应力锥的切削。邢忠海等[2]设计了电缆切削装置，包括驱动机构和切削机构，切削机构包括圆筒状的连接段和锥状的切削段，切削段的内壁上设有至少1个刀片，另一端与驱动机构相连并设有手持机构；与现有人工相比，切削出的反应力锥的表面形状更加规则，但是仍需要人工保持装置的平衡。姚德利[3]设计了一种新型反应力锥剥切器，主要结构由刀体、手柄、刀片、调节螺母等组成；刀片能够灵活调节，用于切削不同尺寸的反应力锥；设备优势在于适应性较好，可以切削多种规格的电缆，但是切削力仍由人工控制。综合分析已有的切削装置，大都以刀片、车刀为切削末端配合人工辅助操作，切削力由人工控制，切削表面质量易受人工影响。

作为切削设备的执行端，切削刀具的选择及切削力的稳定性尤为重要。合适的切削方式不仅能提高切削效率，还能改善反应力锥表面质量。本文中通过分析反应力锥的形状及材料性能，选择合适的切削刀具及切削方式。采用ABAQUS软件的显式模块，对切削过程中所需要的扭矩进行仿真，并建立切削力响应曲面模型，选取合适的切削参数，保证切削过程的平稳性。

1 反应力锥

1.1 反应力锥结构

海底电缆是用绝缘材料包裹的电缆，铺设在海底，主要用于水下大功率电能的传输[4]。在制作接头之前，需要将电缆端部绝缘层切削成锥状，切削出的反应力锥表面要求形状规整。如果切削表面存在缺陷，在电场影响下极易形成放电通道，导致表面放电，进而造成击穿[5-6]。图1所示为切削后的海底电缆反应力锥结构。

图1 切削后的海底电缆反应力锥结构

反应力锥的表面形状理论上是复对数曲线。在实际的工厂切削中，不易切削出复杂曲线，因此企业规定了一定的工艺尺寸，由直线代替反应力锥曲线。

1.2 绝缘层材料性能

海底电缆绝缘层一般采用交联聚乙烯(XLPE)材料。绝缘材料XLPE的应力-应变曲线如图2所示。从图中可以看出，应力-应变曲线分为弹性区和塑形区2个部分，弹性区对应曲线刚开始阶段，应变基本不变，应力急速增大，在应力为12 MPa时进入塑性区。塑性区内的应力-应变关系较复杂，试样先后经历应变软化、细颈及趋向硬化的过程。最后在应力为24 MPa时，试样被拉断，对应的应力即为拉伸强度[7]。

图2 绝缘材料交联聚乙烯的应力-应变曲线

2 切削方案制定

2.1 刀具选取

XLPE属于热固性材料，加热后不易熔化。切削热固性材料与切削脆性金属的过程类似，切屑变形时不存在塑性变形区，切屑呈崩碎状[8]。由于塑料的导热系数较小，切削时产生的热量不能及时散发，热量容易聚积于刀刃，因此对于XLPE材料的切削，宜采用前角较大的刀刃工具，并且刀具材料选用导热系数大的高速工具钢[9-10]。

由于海底电缆本身质量大，不能回转，因此需要刀具本身进行自转和公转才能完成反应力锥的切削。考虑到切削效率以及刀具散热问题，选择圆柱形铣刀以及周铣的方式进行切削反应力锥。图3所示为齿数为12的圆柱形铣刀的主视图与侧视图。

(a)主视图

圆柱形铣刀具有刀齿多、刀刃前角大、刀刃总长度大、多刃旋转切削温度低等特点。切削方式采用更容易切下切削层的顺铣方式，切削过程中切削层厚度由大到小，刀齿磨损较少，在保证反应力锥表面质量的同时提高刀具耐用度[11]。

2.2 切削方式确定

切削反应力锥过程中应避免刀具伤及线芯。 线芯出现损伤后， 在实际应用时会导致电荷集中， 劣化接头电气性能， 同时综合考虑切除效率以及反应力锥的形状， 因此切削形式采用螺旋进给的切削方式， 如图4所示。 在切削绝缘过程中， 刀具转速为n， 刀具轴线与海底电缆轴线夹角固定并围绕电缆旋转， 转速为ω， 同时沿海底电缆轴线螺旋进给， 进给速度为v。

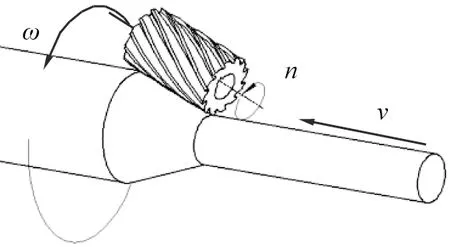
v—轴向进给速度； n—刀具转速； ω—回转角速度。

3 基于ABAQUS软件的切削仿真

3.1 切削力分析

在刀具总切削过程中，主运动的回转轴线所产生的扭矩为切削力，直接影响着工件质量、刀具寿命、机床动力消耗等因素。切削力的变化通常与很多因素有关，不同的切削参数以及工件曲率的变化均对刀齿的进刀角、退刀角和切削厚度造成影响，进而影响切削力的大小。研究切削用量的优化选择对减小切削力具有重要的指导意义[12-14]。

圆柱形铣刀切削过程中的切削力如图5所示。铣削力R为主切削力，正交分解为R1、R2，R1、R2分别为工件对刀具的支撑力、进给抗力[15-16]。

vf—工件速度； R—主切削力； R1、 R2—主切削力的正交分力； n—刀具转速。

3.2 有限元模型建立

利用Solidworks软件建立三维模型，并将模型导入ABAQUS软件。在切削过程中，刀具切削宽度逐渐增大，当切削宽度最大，即完全切出锥体时，切削力达到稳定，并且取得最大值。本文中直接建立海底电缆切削力达到稳定时的有限元模型。

建立有限元模型基于以下假设条件： 1)不考虑工件和刀具的振动； 2)不考虑切削温度对切削力的影响； 3)忽略加工过程中受温度导致的材料属性变化。

建立的切削反应力锥有限元模型如图6所示。刀具为解析刚体，工件设定为可变形体。建立参考点及刀具坐标系，以便于施加边界条件及输出切削扭矩。

图6 海底电缆切削反应力锥有限元模型

3.3 材料塑性定义

XLPE绝缘材料参数如下：密度为1 400 kg/m3，泊松比为0.38，屈服应力为12.2 MPa。

分别定义ABAQUS软件中材料的弹性和塑性，塑性定义中的应变指塑性应变，需要用真实应力-应变曲线中的应变减弹性应变得到。一般地，在材料试验测试时，测出的试验曲线是名义应力-应变曲线，真实应力应变可由图2中名义应力-应变曲线转换得到[17]。

真实应变ε与名义应变εnom之间的关系为

ε=ln(1+εnom)

。

(1)

真实应力σ、 名义应力σnom与名义应变εnom之间的关系为

σ=σnom(1+εnom)

。

(2)

选用剪切破坏(shear damage)定义材料失效准则。输入相应的断裂应变、剪切应力率和应变比率，损伤演化的类型为位移，给定值为0，表示一旦有损伤萌生即判定单元失效。材料剪切失效的剪切应力率θs为

θs=(q+kspq)/τmax

，

(3)

式中：q为Mises等效应力；ks为剪切应力系数；p为静水压力；τmax为最大剪切应力。

3.4 网格划分

图7所示为圆柱形铣刀及海底电缆反应力锥模型的网格划分。切削绝缘属于显式三维应力分析，绝缘力锥采用四面体网格划分，网格类型选为C3D10M；以圆柱形铣刀作为壳体，采用三角形网格划分，网格类型选为R3D3；采用种子布局的方式进行网格调整，将刀具与绝缘接触面细化，以提高计算精度，缩短运算时间。

图7 圆柱形铣刀及海底电缆反应力锥模型的网格划分

3.5 边界条件设定

采用圆柱形铣刀进行铣削应力锥时，刀具的进给是围绕海底电缆的圆周运动。由于刀具与海底电缆轴线存在夹角，因此铣刀齿在各处的每齿进给量不同，本文中涉及的每齿进给量均为铣刀远离铜导端的每齿进给量。XLPE材料的布氏硬度HB为100，质地较软。为了研究实际切削力受参数的影响变化，在圆柱形铣刀铣削相应硬度材料的推荐参数的基础上，扩大研究范围。确定参数的范围如下：每齿进给量fz(z为刀具齿数)为0.10～0.30 mm， 切削速度为30～120 m/min， 本文中选取的圆柱形铣刀外径为50 mm， 因此选择转速为200～800 r/min。综合切削反应力锥时切削效率及公件曲率，选择侧吃刀量研究范围为2～6 mm[18-19]。

设定仿真切削初始参数如下：添加铣刀转速为300 r/min，侧吃刀量为6 mm，刀具进给速度为0.011 61 m/s。 为了便于加载，将刀具进给速度等效为海底电缆旋转角速度，取值为0.27 rad/s。

3.6 仿真结果

基于ABAQUS软件的切削仿真结果云图如图8所示，图9所示为刀具切削过程中扭矩随时间的变化。从图9中可看出，刀具在时间步长约为0.005 s时切入工件，在时间步长为0.01 s时，切削刃接触长度达到最大，并且切削扭矩趋于平稳，约为2.0 N·m。

图8 基于ABAQUS软件的切削仿真结果云图

图9 刀具切削过程中扭矩随时间的变化

4 切削力的响应曲面分析

4.1 响应曲面模型建立

响应面中存在对应关系的试验点为(x1,x2,…,xi,y)，其中i为试验因素个数，y为响应指标，本文中因素个数为3，响应指标为切削扭矩。选取试验点的原则有多种，本文中采用应用较广泛的中心复合设计取点法[20]。

根据3.5节中确定的参数研究范围，计算各水平对应的比例数值，建立因素水平表，如表1所示。

表1 切削力的响应曲面因素水平设计

将表1导入Design-expert软件，自动生成试验设计方案。设计方案由6个轴点、 8个析因点、 6个中央点组成。共20组试验方案[21]。表2所示为各因素设计方案及仿真结果。

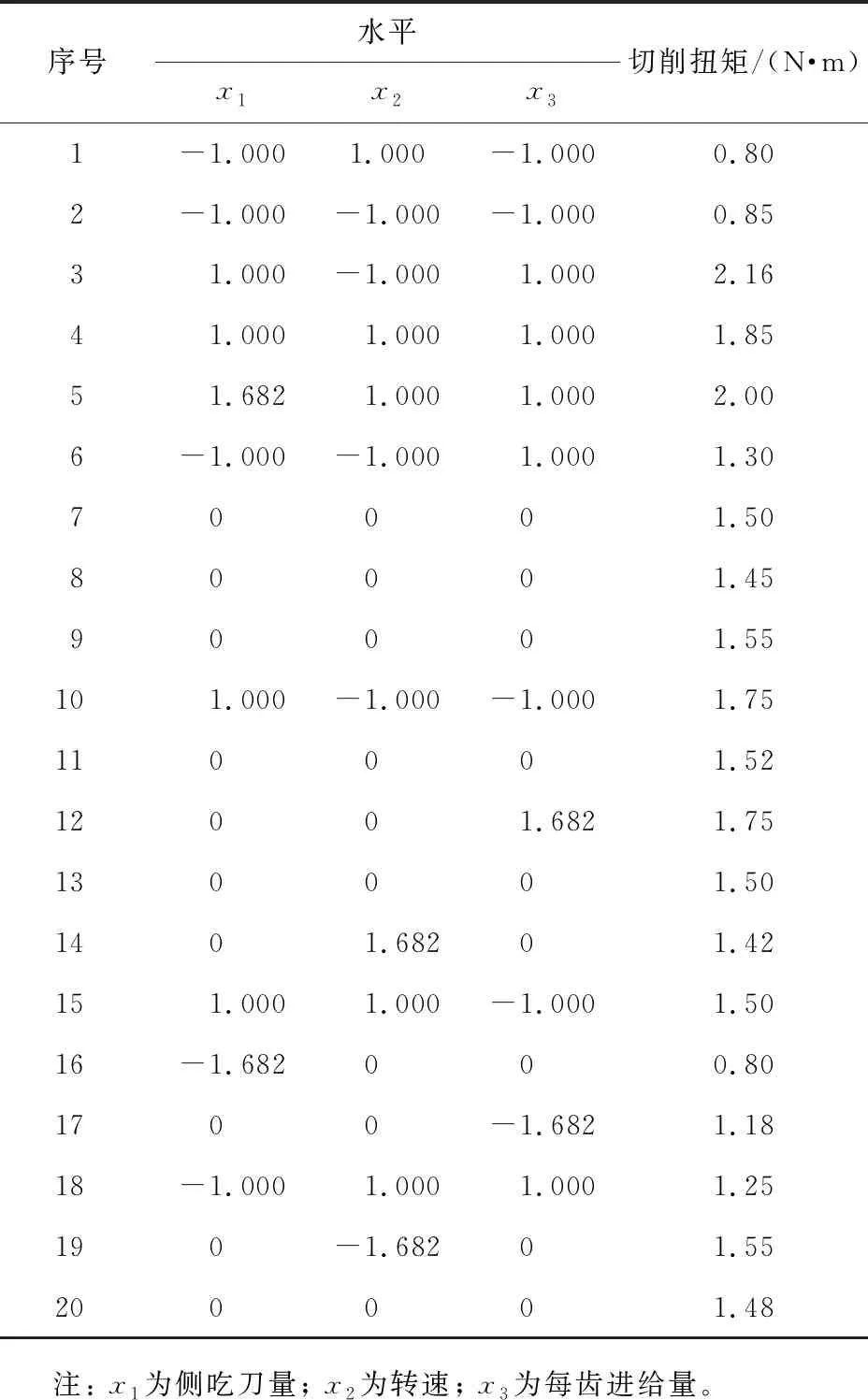
表2 各因素设计方案及仿真结果

利用Design-expert软件对试验点进行回归分析，结果如表3所示。

分析表3中对应项回归关系显著性检验值p值，如果p≤0.05则该项对影响显著；若p≤0.01，则该项对切削扭矩的影响极其显著；若p>0.05，则该项对切削扭矩影响不显著；一般将不显著项剔除，重新进行回归分析[22]。表4所示为修正后回归分析结果。

表3 切削力回归分析结果

表4 修正后回归分析结果

如果拟合模型中p≤0.05， 说明切削扭矩与切削参数的回归关系是显著的； 如果p≤0.01， 说明回归关系是极其显著的； 如果p>0.05， 说明回归关系是不显著的， 建立的回归方程不能用。 从表4中可以得出， 回归方程拟合效果极其显著， 回归方程可用。

建立响应值与自变量之间的拟合表达式，获得切削扭矩的二次多项式回归方程为

y1=1.48+0.37x1-0.067x2+

(4)

式中：x1为侧吃刀量；x2为转速；x3为每齿进给量；y1为切削扭矩的拟合值。

由回归分析的p值可得，各因子的贡献率均很显著，切削扭矩受切削参数影响显著。图10所示为单因素对切削扭矩的影响趋势。从图中可以看出，切削扭矩随着每齿进给量和侧吃刀量的增加而增大，侧吃刀量的影响更大。铣刀转速对切削扭矩的影响最小，转速增大时切削扭矩略有减小。各因素对切削力影响由大到小的排序为侧吃刀量、每齿进给量、转速。

(a)转速

根据表3可以得出，除单因素外，只有侧吃刀量与铣刀转速的交互作用对切削力影响显著。图11所示为交互作用响应曲面模型。从图中可以看出：当侧吃刀量较小时，转速对切削力的影响很小；当侧吃刀量增大时，随着转速的减小，切削力更大。

图11 交互作用响应曲面模型

4.2 切削参数优化

切削参数直接影响切削扭矩的大小。为了保证切削质量以及切削的稳定性，需要制定合理的切削参数以减小切削扭矩。由响应曲面模型分析可知，可以通过减小侧吃刀量和每齿进给量的方式减小切削扭矩，但是切削效率也会随之降低。

切削效率可用切削反应力锥所消耗的时间来衡量。以切削耐压等级为110 kV的海底电缆为例。海底电缆绝缘层外径为86 mm，按照软接头制作要求，单侧海底电缆反应力锥切削后裸露铜导长度约为200 mm，则切削单个应力锥所需时间t(单位为min)为

(5)

式中：d为绝缘层外径；l为裸露导体长度。

将初始切削参数代入式(5)，计算可得切削反应力锥所需时间为36.55 min。

将切削用时和切削力共同作为试验指标。将20组切削试验参数分别代入式(5)，将结果导入Design-expert软件，通过拟合得到切削时间的回归方程为

y2=32.96-13.19x1-17.09x2-10.63x3+4.79x1x2+

(6)

式中y2为切削用时的拟合值。

通过Design-expert软件的响应面优化模块，对切削参数进行优化，参数优化范围及优化目标如表5所示。考虑到绝缘导热系数较小，因此减小切削速度有助于控制切削温度，延长刀具寿命，避免材料粘刀[23-24]。

表5 参数优化范围及优化目标

由Design-expert软件求解得到，当侧吃刀量为2.25 mm，转速为520 r/min，每齿进给量为0.28 mm时，切削扭矩较小，数值为1.18 N·m，切削所需时间为37.92 min。为了验证响应面优化的准确性，利用ABAQUS软件对优化参数进行切削仿真，结果如图12所示。由图可知，所需切削扭矩为1.1 N·m。根据式(5)可得切削时间为40.21 min。拟合值与仿真值的误差约为6%。优化前、 后切削参数及效果如表6所示。由表可知，优化后切削扭矩减小了45%，切削用时延长了9%。

图12 优化后切削扭矩随时间的变化

表6 优化前、 后切削参数及效果

5 结论

1)通过分析XLPE材料性能，选择圆柱形铣刀作为切削刀具，采用围绕海底电缆轴线螺旋进给的方式切削反应力锥。

2)通过ABAQUS软件仿真，得出圆柱形铣刀在给定切削参数条件下切削反应力锥过程中所需要的切削扭矩为2.0 N·m。

3)在保证切削效率的同时减小切削扭矩， 运用响应面优化法对铣削参数进行优化设计， 优化后的切削参数如下： 侧吃刀量为2.25 mm， 转速为520 r/min， 每齿进给量为0.28 mm； 新的切削参数条件下切削扭矩为1.1 N·m， 切削所需时间为40.21 min。 相比优化前， 切削扭矩减小了45%， 切削用时延长了9%。