基于遗传算法-神经网络的豆渣酶解工艺优化及其动力学研究
谢春平,赵良忠, ,李 明,周晓洁,黄展锐,莫 鑫,车丽娜,庾 坤
(1.邵阳学院食品与化学工程学院,湖南邵阳 422000;2.豆制品加工与安全控制湖南省重点实验室,湖南邵阳 422000;3.湖南省果蔬清洁加工工程技术研究中心,湖南邵阳 422000;4.广州佳明食品科技有限公司,广东广州 511458)
豆渣是大豆制品加工过程中的主要副产物,其营养成分丰富[1−2],其中被誉为“第七大营养素”的膳食纤维约占豆渣干物质的60%[3−5]。但由于口感粗糙、水分含量极高(达85%),不易储藏,有效利用率低,大部分豆渣被直接丢弃,不仅浪费资源,还污染环境[6]。据中国豆制品行业协会数据统计,2019年用于豆制品加工的大豆约为800万吨,以加工1吨大豆产生1.5吨湿豆渣计,豆制品加工年产湿豆渣量在1200万吨以上[7−9]。巨量的豆渣如何进行利用,提高其附加值,是值得研究的课题之一。
研究表明,利用酶可提取豆渣中的可溶性膳食纤维(SDF)[10]、不溶性膳食纤维(IDF)[11]、多糖[12]、大豆多肽[13]等。目前酶水解豆渣的研究主要是不完全水解产物(SDF、多糖等)的工艺优化及应用,而植物纤维酶解动力学也是倾向于玉米芯[14]、燕麦壳[15]、小麦秸秆[16]等,关于豆渣酶解生成还原糖的工艺及其酶解动力学的研究鲜为报道。常见优化方法有正交试验设计[17]、响应面优化设计(RSM)[18−19]、人工神经网络(ANN)[20]等,几种方法各有优劣但未见讨论不同优化方法对豆渣酶解效果的影响。
因此,本文主要研究在豆渣酶解过程中p H、纤维素酶添加量、酶解温度和酶解时间对还原糖生成量的影响,通过RSM与GA-ANN两种方法优化出豆渣酶解生成还原糖的最佳工艺。并且在豆渣酶解优化工艺的基础上,进一步研究豆渣的酶解动力学,以期为豆渣高效利用和后期全豆豆腐产品研究提供技术理论支持。
1 材料与方法
1.1 材料与仪器
豆渣 熟浆工艺生产豆浆所得的副产物,豆制品加工与安全控制湖南省重点实验室提供;FDY-2243型纤维素酶 酶活11000 U/mL,夏盛实业集团有限公司。
MZJJ-1型熟浆生产设备 北京康得利智能制造有限公司;QDSJ9000-2型湿法超细精磨机 无锡轻大食品装备有限公司;Atomo3.0型均质机BERTOLI;UV-1780型紫外可见分光光度计 日本岛津公司。
1.2 实验方法
1.2.1 原料预处理 采用机械粉碎的方法处理豆渣。选取新鲜的豆渣(水分含量为79.3%),添加3倍豆渣质量的水进行湿法粉碎,再将粗粉碎后的豆渣液进行均质,均质压力为35 MPa,物料经均质后,待用。
1.2.2 单因素实验 以预处理豆渣液100 g为基准,分别以p H、纤维素酶添加量、酶解温度、酶解时间四个因素进行单因素实验,以还原糖生成量作为评价指标,探究各因素的较优水平。固定p H为5.4、纤维素酶添加量为4%、酶解温度为55℃、酶解时间为2 h,实验水平设定pH为4.5、4.8、5.1、5.4、5.7、6.0;纤维素酶添加量为1%、2%、3%、4%、5%、6%(以豆渣液干物质的量计算);酶解温度为40、45、50、55、60、65℃;酶解时间为1.0、1.5、2.0、2.5、3.0、3.5 h。
1.2.3 响应面试验 在单因素实验基础上,选取各因素较优水平,以还原糖生成量为响应值,根据Box-Benhnken设计原理,进行4因素3水平响应面优化试验。试验设计如表1所示。

表1 响应面试验设计Table 1 Response surface experimental design
1.2.4 人工神经网络(ANN)模型构建 本研究采用3层的ANN模型创构建实验的优化模型,三层网络的结构分别由输入层、隐含层和输出层构成[11,21]。将p H、纤维素酶添加量、酶解温度和酶解时间设定为输入层神经元,还原糖生成量设定为输出层神经元,以“traingdm”为训练函数,29组RSM数据为实际样本,各变量增加±Δi(Δi=0.2%),采用正交L8(27),生成232个虚拟样本,结合29组实际样本,共261组样本作为训练样本,从上至下的230组数据的60%用于训练、20%用于检验、20%用于测试[22]。其中隐含层神经元数目使用经验公式(1)计算得到,其中m为隐含层神经元个数,n为输入层神经元个数,l为输出层神经元个数,a为[1,10]的常数。

1.2.5 遗传算法(GA)优化最佳工艺参数 将遗传算法与ANN构建的模型结合,进行全面仿真实验,以寻求豆渣酶解工艺的最佳工艺参数组合及最大的还原糖生成量的值。设定种群大小为50,最大遗传代数150,代沟0.9,交叉概率为0.5,变异概率为0.05,运行matlab软件程序,得到每代种群适应度及其变化结果。
1.2.6 酶解动力学 假设酶解反应速率与时间呈一种幂函数关系,同时将纤维素酶水解看成拟态一级反应,则酶解动力学可以表示为[23−25]:

其中酶解速率常数为:

式中:S0为初始浓度,g/kg;t为酶解时间;K0为与时间无关的常数;h为分形维数,描述底物颗粒不规则程度的参数;0.9为木质纤维素转变为还原糖的系数。
1.3 还原糖含量测定及生成量计算
按照3,5-二硝基水杨酸法测定[26]。在6支试管中分别加入1 mg/mL葡萄糖标准溶液0、0.10、0.20、0.30、0.40、0.50 mL,补蒸馏水至0.5 mL,然后加入DNS试剂1.5 mL,充分混匀。置沸水浴中煮沸5 min,然后迅速流水冷却,并分别向试管中加入4 mL蒸馏水,混匀。在540 nm处读OD值。以葡萄糖浓度(μg/mL)为横坐标,以OD值为纵坐标制作标准曲线,得到其线性回归方程。吸取0.5 mL样品液,按照上述步骤操作测定OD值,并代入回归方程中计算样品中的还原糖含量。
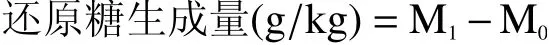
式中:M0为豆渣中初始还原糖浓度,g/kg;M1为酶解反应完成后豆渣中的还原糖浓度,g/kg。
1.4 数据处理
采用Design Expert V 8.0.6、IBM SPSS Statistics22.0、Excel 2017、Origin 2018进行试验设计和数据分析,Matlab 2016a软件实现神经网络和遗传算法。且每组实验重复3次。
2 结果与分析
2.1 葡萄糖标准曲线的建立
以葡萄糖浓度(x)为横坐标,吸光度为纵坐标(y)绘制标准曲线,线性拟合方程为y=0.551x−0.0027(R2=0.9983)(图1)。结果显示葡萄糖标准溶液0~0.5 mg/mL内与吸光度的线性关系较好。
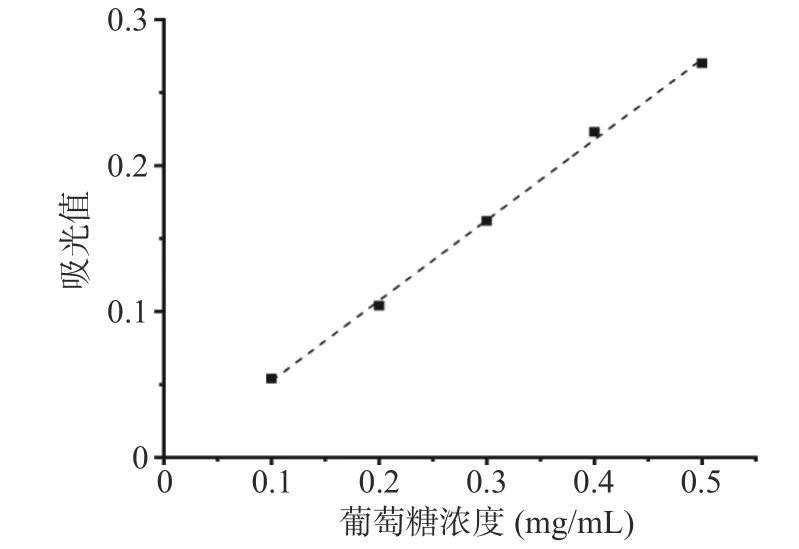
图1 葡萄糖标准曲线Fig.1 Glucose standard curve
2.2 单因素实验结果
由图2A知,当豆渣液p H为4.5~5.1时,豆渣酶解效果随溶液p H的增大而增强;pH为5.1时,豆渣酶解效果最佳;当pH为5.1~6.0时,豆渣酶解效果逐渐减弱。p H会影响酶分子上酸性和碱性氨基酸残基的侧链基团和底物的解离状态,进而影响酶与底物的结合[27−28]。

图2 单因素实验结果Fig.2 Single-factor experimental results
纤维素酶使豆渣中的不溶性膳食纤维分子链被切断,分子量降低,一部分不溶性膳食纤维变成水溶性膳食纤维,然后被水解成还原糖。由图2B知,随着纤维素酶添加量的增加,酶与底物的接触机率增大,从而加速了反应进程[29];纤维素酶添加量达到4%后,还原糖生成量的增加趋势趋于平缓,无显著差异(P>0.05)。这可能是因为随着酶解产物的增加,产物与酶结合,阻碍了底物与酶的结合,减缓了酶解反应进程[30−31]。出于实验成本考虑,选择纤维素酶添加量4%为最适添加量。
由图2C知,随着酶解温度的升高,豆渣酶解效果逐渐加强,当酶解温度达到50℃时,酶解效果达到最佳,继续升高酶解温度,酶解效果显著减弱(P<0.05)。这是因为酶在低于最适温度时,升温会使反应体系内的物质运动加快,提高底物与酶的接触几率,但在最适温度后,维持酶分子结构的次级键就会随着温度的升高开始断裂,酶反应速率降低[32]。
由图2D知,当酶解时间1.0~3.0 h时,还原糖生成量随着酶解时间的延长而明显增多,酶解时间在达到3 h以后,还原糖生成量变化不显著(P>0.05),可能是因为随着酶解时间的延长,酶作用越充分,豆渣浓度降低、部分酶逐渐失活以及酶解产物的反馈抑制作用增强,从而影响酶解反应的进行[33]。因而选择酶解时间3 h为最适反应时间。
2.3 响应面试验
2.3.1 响应面结果 响应面实验结果见表2。以还原糖生成量为响应值,利用Design Expert V 8.0.6统计软件对试验结果进行多元回归拟合,得到关于还原糖生成量与各个因素的回归方程的预测模型:Y=+2.42−0.4A+0.20B+0.1C+0.049D−0.045AB+0.068AC−0.045AD−0.14BC−0.007BD−0.035CD−0.18A2−0.21B2−0.14C2−0.23D2

表2 响应面试验结果Table 2 Results of the response surface experiment
2.3.2 方差分析 以还原糖生成量为响应值进行方差分析,结果见表3。显著性检验结果显示,还原糖生成量回归模型差异极显著P<0.0001,失拟值0.3641(P>0.05),表现为不显著,说明试验值和预测值的误差较小。决定系数R2=0.9580,因变量和自变量之间的线性关系显著,回归方程拟合度较高。模型的校正决定系数R2Adj=0.9161,表明有8.39%的情况不能对该模型进行解释。在对还原糖生成量的影响上,A、B、C、A2、B2、C2和D2均达到极显著水平(P<0.01),BC达到显著水平(P<0.05),其中D、AB、AC、AD、BD和CD均为不显著因素(P>0.05)。由F检验可以看出A、B、C、D四个因素对还原糖生成量的影响为A>B>C>D,即p H>纤维素酶添加量>酶解温度>酶解时间。

表3 回归模型方差分析Table 3 Regression model variance analysis
2.3.3 交互作用分析 响应曲面越陡峭,表明该因素对响应值的影响越大[34],等高线的形状反映两因素之间交互作用的显著程度[35−36]]。由交互作用可知,纤维素酶添加量(B)与酶解温度(C)对还原糖生成量的影响显著(P<0.05,见图3),p H(A)与纤维素酶添加量(B)、p H(A)与酶解温度(C)、pH(A)与酶解时间(D)、纤维素酶添加量(B)与酶解时间(D)、酶解温度(C)与酶解时间(D)的交互项对还原糖生成量的影响均不显著(P>0.05),这与方差分析结果一致。

图3 各因素交互作用对还原糖生成量的响应曲面Fig.3 Response surfaceof the interaction of variousfactorsto the reduction of sugar production
2.3.4 RSM最佳实验结果及验证实验 豆渣酶解工艺经Design Expert.V 8.0.6软件分析得出最佳参数为:p H4.83、纤维素酶添加量为4.33%、酶解温度为51.60℃和酶解时间3.09 h,在此条件下还原糖生成量为2.68 g/kg。根据生产实际调整确定最佳工艺参数为pH4.8、纤维素酶添加量4.3%、酶解温度52℃、酶解时间3.1 h,在此条件下进行豆渣酶解工艺优化的验证实验(n=3),得到RSM实际还原糖生成量为2.54 g/kg。
2.4 ANN模型的建立与训练
由公式(1)与其实际意义得隐含层神经元个数取值范围为[3,13],设定ANN训练学习次数10000次,学习速率为0.35,动量常数为0.54,训练步长100,直至目标误差达到0.00001时训练结束,寻找到测试集MSE的最小值,得到隐含层神经元个数为9。
人工神经网络训练出的模型,其拟合回归系数R值表示目标数据和输出结果的相关程度。由图4可知,训练、验证、测试、与全数据图中r值分别为0.99451、0.99413、0.99374、0.99432,在现有设置的参数下,模型拟合结果具备优良的随机验证效果。r预测>0.90,说明神经网络模型不存在欠拟合状态;因此,可认为该模型具有较强的解释能力和较低的仿真误差,能较好地训练、预测和整体拟合效果。

图4 训练模型适配Fig.4 Training model fit
2.5 GA寻优及验证豆渣酶解工艺结果
通过ANN模型调试函数的适应度,以还原糖生成量作为其函数的输出值,将ANN与GA结合对酶解工艺进行寻优,获取最佳的豆渣酶解工艺。
由图5可得,当进化代数增大至46代时,GA停止选择并得出适应度值最高的个体。运行出的优化结果:最优工艺参数为pH5.22、纤维素酶添加量4.38%、酶解温度51.91℃、酶解时间3.19 h,还原糖生成量预测最大值为2.67 g/kg。考虑实际操作,将工艺修改为p H5.2、纤维素酶添加量4.4%、酶解温度52℃、酶解时间3.2 h,在此条件下进行验证实验(n=3),得还原糖生成量值为2.65 g/kg。

图5 适应度曲线Fig.5 Adaptability curve
2.6 RSM和GA-ANN预测结果对比
RSM和GA-ANN模型预测的还原糖生成量见表4。使用Excel对实测值与预测值作图(见图6),分别计算RSM和GA-ANN的决定系数R2、RSS与RMSE[37−39]],为0.9583、0.1434、0.0703和0.9825、0.0353、0.0349,R2、RSS越高,RMSE越小,模型越稳健、预测效果越好;由表4可知,GA-ANN优化结果比RSM优化结果高,表明使用GA-ANN优化豆渣酶解工艺是可行的,GA-ANN模型比RSM的拟合度高、估计预测能力也相对精准。

图6 模型预测值与实际值对比Fig.6 Compared of model predicted value and actual value

表4 RSM与GA-ANN优化结果比较Table 4 Comparison of RSM with GA-ANN optimization results
2.7 豆渣酶解动力学
用类分形动力学方程式对豆渣酶解实验数据进行一元回归拟合,得拟合曲线如图7和动力学参数k0为0.5372、分形维数h为0.1530,实验数据与方程拟合度达到0.9827,拟合效果良好。酶解速率常数反应过程的快慢,根据所得动力学参数k0与分形维数h,可得酶解速率常数随时间变化的曲线,见图8,由于酶的活性、底物与生成物含量变化等因素影响,酶解反应速率随着酶解时间的增加而不断降低。
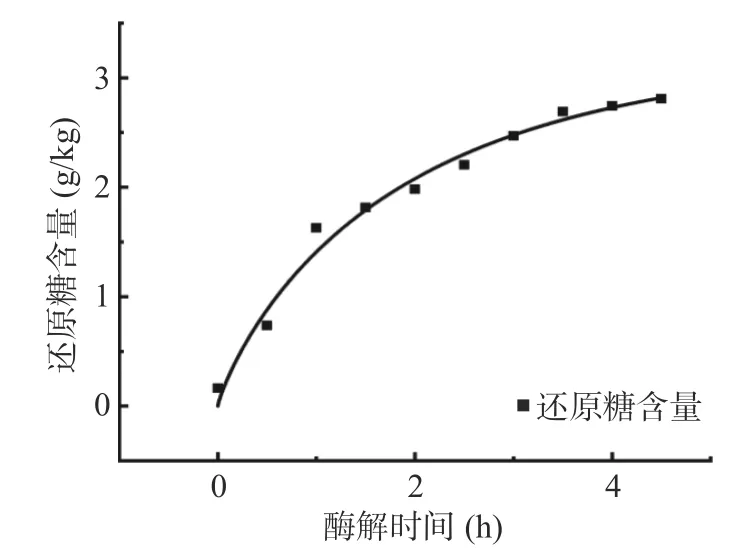
图7 酶解动力学曲线Fig.7 Enzymatic dynamicscurve

图8 酶解速率常数曲线Fig.8 Enzyme rate constant curve
3 结论
本研究通过RSM与GA-ANN两种方法优化出豆渣酶解生成还原糖的最佳工艺为p H5.2,纤维素酶添加量4.4%,酶解温度52℃,酶解时间3.2 h,此条件下还原糖生成量为2.65 g/kg。通过类分形动力学建立了豆渣的酶解动力学模型,该模型的R2达到0.9827,拟合效果良好。本实验为豆渣的高效利用和后期全豆豆腐研究提供了理论支撑,但豆渣酶解生成的还原糖组分及其在全豆豆腐中的作用机制不明,还有待进一步分析研究。

