时差法超声波热能流量表的高精度补偿算法研究
黄军垒,李国文,王普杰,张雷,李银华,袁超
1.郑州斯倍思机电有限公司, 河南 郑州 450007;2.河南开放大学, 河南 郑州 450003;3.郑州轻工业大学 电气信息工程学院, 河南 郑州 450002;4.河南农业大学 理学院, 河南 郑州 450002
0 引言
热能流量计广泛应用于冶金、化工、轻工业等国民经济基础行业[1],对国民经济发展有重要支撑作用.随着企业生产规模不断扩大,生产系统结构越来越复杂,为保证工业生产安全运行,需要对关键生产参数进行实时监控和测量.此外,随着国家节能减排政策的出台,企业对能源综合利用、余热回收计量也提出了更高要求.但受工业现场环境恶劣、生产工艺结构复杂,以及多通道、流量不稳定等因素影响,热能流量计难以准确测量[2-3],无法实现工业过程的稳定控制和及时优化.因此,研究流量计高精度补偿方法,对企业实现智能制造和降本增效具有积极作用.
目前,在工业生产中大多仍采用结构简单的传统机械式仪表,而机械磨损会导致其精度下降、维护成本升高、使用寿命缩短等问题.近年来,随着人工智能、智能仪器仪表等新兴技术的不断发展,超声波热能表、涡轮热能表、涡街热能表等先进传感器在制造业中获得了成功推广和应用[4-10].其中,超声波流量表是一类非接触式仪表,精度高、功耗低、使用寿命长,成为业界研究热点.
超声波流量表的常用测量方法包括时差法、噪声法、多普勒法等.时差法超声波热能流量表是一种新型智能检测仪,但受声道数量、管道内流速稳定性及变化率等因素的影响,仪器在低流速状态下存在检测灵敏度不足、稳定性较差、测量精度低等问题,需要对其进行及时校准和补偿.但该方法依赖技术人员的主观经验,效率低,特别是随着工厂规模的不断扩大,现场包含的大量仪器仪表维护困难,造成技术人员的劳动强度增大.针对上述问题,国内外学者开展了大量研究[11-17].文献[13]提出了基于卡尔曼滤波的数据滤波算法,可显著降低测量误差,提高水表检测精度.文献[14]提出了一种基于BP神经网络的补偿算法,应用于超声波热量表中,取得良好的补偿效果.虽然BP神经网络具有较强的泛化能力,但算法收敛速度慢,且易陷入局部最优解[18].然而,由于工业现场环境恶劣,仪器易受外界干扰,上述方法在实际应用中存在一定局限.
鉴于此,本文拟提出一种基于改进Lagrange算法的时差法超声波热能流量表自适应补偿算法,以期解决仪器低流速状态下检测失效难题,实现高精度检测.
1 时差法测量原理
时差法测量的基本原理是依据超声波在流体中沿同一声道顺向和逆向传播产生的时间差与流体流速之间的线性关系,通过检测流经两个检测装置的时间差测量流速,其测量示意图如图1所示.其中,L为传输长度,t2和t1分别为顺流和逆流时间,α为声道与水流夹角.

图1 时差法测量示意图Fig.1 Schematic diagram of time difference measurement
单管道中,水流平均速度v为
其中,c为超声波速度.
多管道中,水流平均流速va为
其中,ωi是不同管道的权重,vi是不同管道的流速.传统的流量qv计算公式为
其中,K是修正系数,S是管道截面积/m2.
一般情况下,修正系数K是根据流速大小而给定的分段式、非连续常数,为提高小流速状态下测量的准确度,将K值与流速进行相关的连续化处理.
其中,K(va)和K(v)是综合系数函数,则热量Qs计算公式为
其中,qm是流经热量表的水的质量流量/(kg·h-1);ρ是流经热量表的水的密度/(kg·m-3);ΔH是进出口温度下水的焓值差/(J·kg-1);τi(i=0,1,2,…)是时间/h.
以单管道、小流速状态下的热量为目标,可得校正后热量Q为
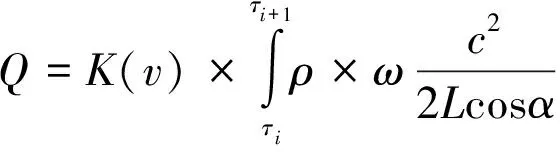
ΔH×dτ=K(v)×Qs
①
2 基于加权Lagrange算法的流量计补偿算法
在公式①中,修正函数K(v)是热量计检测关键,对仪器检测准确性有重要影响.传统线性补偿方法(如分段补偿、最小二乘拟合法则等)能基本拟合修正函数曲线,改善补偿效果,但泛化表达能力有限,对于复杂工业场景,其精度难以满足生产要求[13-14].因此,为解决低流速下检测失效问题,本文基于Lagrange算法的补偿模型,提出了一种新的通过权重因子调节函数分布以实现自适应补偿的算法.
Lagrange算法的原理[19]是以曲线上任取相邻3个点作为插值节点,以二次曲线近似表示原曲线.在任意相邻两节点间作插值,考虑到插值点左右两侧的插值节点不同,曲线的趋势也不同.因此,为增加修正函数K(v)表达能力,提出一种加权Lagrange二次插值算法,其思想是采用加权方式将插值节点两侧的两条曲线融合成一条插值曲线,以获取更加精准的测量信息.
基于加权Lagrange算法的修正函数K(v)表达如下所示:
其中,lm(v)是拉格朗日插值基函数,WL(v)和WR(v)分别是左右两侧的权重因子.其定义式分别为
WL(v)=(v-vm+2)2[2(v-vm+2)+
3(vm+2-vm+1)]/(vm+2-vm+1)3
WR(v)=(v-vm+1)2[2(v-vm+1)+
3(vm+1-vm+2)]/(vm+2-vm+1)3
由于采用的是Lagrange二次插值,即在vk-1、vk、vk+1三点进行二次插值,插值点v∈(vk,vk+1),故二次插值函数为
余项为
R2(v)=f(v)-P2(v)=
设vk+0.5是vk,vk+1的中点,此流速状态下的流速范围是0~1.0 m/s,采样间距为0.1 m/s,则在vk+0.5左右两侧的插值余项分别为
在低流速状态下,由于流速变化较为缓慢,故采样点也相对较多,所以任意相邻两点之间的变化不大,在流速范围内的加权Lagrange抛物线插值补偿公式为
其中
当插值点出现波动时,G(RL,RR)可以确定误差补偿的方向.若RL和RR异号,证明在插值子区间内存在转折点;若RL和RR同号,则选取较小的值作为误差补偿参数,可对误差进行有效补偿.该方法具备一定自适应性.
3 仿真结果与分析
本文选取国内某热力厂实际生产数据进行仿真实验,具体实验环境如下所示:Windows 10 Professional (64 bit) OS; Intel(R) Core (TM) I7-8770 3.20 GHz CPU; RAM 16.0 GB; Matlab version 2018a.
为验证本文加权Lagrange流量计补偿算法的有效性,选取基于常数K校正和Lagrange校正进行仿真对比分析.为合理评价算法性能,选取误差(E)和相对误差(RE)两个指标进行评价,定义如下:
E=y-yi
其中,y和yi分别代表实际值和校正值.
首先,查询Ceebic-4型号超声波热能表中各流速点对应的内设默认K值与传统常数校正K值表.在低流速状态下(0~1.00 m/s),选取的部分流速点及对应修正系数K值如表1所示.

表1 流速点及对应修正系数K值Table 1 Velocity point and correction coefficient K
不同校正算法下K值趋势线如图2所示.由图2可知,常数K校正方法是阶梯型、分段非连续值,泛化能力有限,补偿效果不佳;采用Lagrange算法和加权Lagrange算法的曲线拟合效果较好,说明这两种算法具备较强非线性表达能力;进一步分析可知,基于加权Lagrange算法的曲线平滑度优于常规Lagrange算法,且误差更小,表明加权Lagrange算法具备强拟合能力.
4 实验结果与分析
4.1 实验平台及环境
实验平台采用LGS-200流量标准装置,其主要功能是用于检测超声波热能表流量计量的精确度.在实验中应用4个Ceebic-4型号的时差法超声波热能表,管径DN200,量程为0~500 m3/h,常用流量为250 m3/h.将出厂默认的程序、传统常数K校正程序、Lagrange抛物线K校正程序、加权Lagrange抛物线K校正程序分别写入这4块热能表,并与LGS-250流量标准装置同时放在温度为15 ℃、相对湿度为13%的室内,且置于流速相同的同一管道上,使实验条件完全相同.
4.2 算法误差分析
从图2中采集10种不同流速状态(见表2)进行实验,同时,为保证实验的准确性与可靠性,在相同测试环境下,每一组流速点分别进行50次实验,取其平均值作为最终实验结果.不同流速下的各校正算法流量对比见表2,其中标准流量值y是LGS-200流量标准装置实测值,y1是未校正流量,y2是常数K校正流量,y3是Lagrange校正流量,y4是加权Lagrange校正流量.

图2 不同校正算法下K值趋势线Fig.2 Trend of K value under different methods
根据表2数据可得其误差和相对误差分别如表3和表4所示.由表3可知,y1检测准确度最差,误差值最大,且误差趋势波动剧烈,表明仪器检测数据在未校正情况下往往失真,易造成一定生产风险;采用常数K校正后,误差明显减小,趋势线波动平缓,但校正精度有限,难以满足生产需求;采用Lagrange校正流量后,精度明显优于上述两种结果,这表明采用Lagrange算法具有可行性;基于加权Lagrange的校正在10种不同流速实验下均取得最佳校准效果,且误差曲线波动平缓,表明本算法具有较高可靠性,能够针对不同流速自适应补偿,从而提高检测精度.

表2 不同流速下各校正算法的流量Table 2 Flow value of various correction algorithms at different flow rates m3/h

表3 不同流速下各校正算法的误差Table 3 Correction errors of various correction algorithms at different flow rates m3/h
4.3 相对误差分析
由表4可知,在小流速状态下,基于加权Lagrange算法的超声波热量表相对误差最小,其最大值仅为0.34%,最小相对误差为-0.03%,能够满足实际生产需求.

表4 不同流速下各校正算法的相对误差Table 4 Relative error of various correction algorithms at different flow rates %
为进一步验证算法有效性,对3种型号(DN20,DN50,DN100)超声波热量表进行检验,随机选取10组不同低流速测试点.结果显示,其中最大相对误差为0.37%,最小相对误差为-0.01%.由此可知,在低流速状态下,基于加权Lagrange算法的相对误差在±0.4%以内,测量精度提高,稳定性得以改善.
5 结论
本文提出了一种基于改进Lagrange算法的时差法超声波热能流量表自适应补偿算法.通过建立热量与修正系数之间的补偿模型,提出了一种基于加权Lagrange算法的拟合修正算法,解决了低流速状态下仪器检测失效难题.基于某热力厂生产数据的实验结果表明,本文算法具有较高的检测精度,能满足生产需求,特别是在低流速状态下,具有一定自适应补偿效果.未来将引入深度学习算法以进一步提高检测精度.

