中贫营养湖泊叶绿素a预测模型探讨
刘 宇,朱丹瑶
(牡丹江师范学院历史与文化学院,黑龙江牡丹江157012)
随着经济的高速发展,我国内陆水体的污染不断加剧,致使一些湖泊藻类物质急剧增多,富营养化状况也日趋严重。藻类的富集与死亡不仅会降低湖泊的功能与作用,还可能通过食物链进一步损害人类身体健康[1]。地表水状况与饮水安全已然成为影响生态与社会发展的重要因素。水质监测作为水污染防治与评价的重要依据,其结果直接影响区域生产与居民生活用水[2,3]。传统的水质监测不仅耗时长,费用高,且难以及时地掌握整个研究区水质的空间分布状况。遥感技术凭借其独特优势已被广泛应用到了水质监测中[4,5]。随着遥感监测研究的日益成熟,水体中可监测指标也在不断增加。在众多水质参数当中,叶绿素a 作为藻类物质的重要组成成分之一,一直是内陆水体富营养化状况监测的重要参数指标[6,7]。
目前,国内外已有不少关于内陆水体叶绿素a浓度的遥感监测研究,但无论采用哪种方法,其研究的范围主要集中在富营养状态的水域,对于中/贫营养状态的水域研究较少。如:在传统经验模型中,Gitelson 等[8]利用植物色素在700 nm 附近荧光峰位置与叶绿素a浓度的变化规律进行建模,估算了浑浊水体叶绿素a浓度;Hoogenboom 等[9]在Ljsselneer湖区,通过分析水体光谱数据发现,波段比值Rrs(708)/Rrs(676)在叶绿素a 浓度建模中精度最高;Ricardo 等[10]通过分析FLH(Fluoresce Line Height)算法在MODIS 影像的应用,发现该算法较依赖于波段位置的准确性。马万栋等[11]利用高光谱数据对比研究发现,反射峰面积模型NPA(Normalized Peak Area)较适合用于实测高光谱数据来反演叶绿素浓度。随着水质遥感研究的不断深入,一些半经验半分析模型也被一些学者采用,常用的模型主要有三波段模型、四波段模型等。如:Dall’Olmo等[12]利用三波段模型通过反演叶绿素浓度证实了该模型在内陆水体中的应用。Le 等[13]通过分析太湖水域悬浮物吸收和散射特性,进一步构建了四波段模型,并取得不错的效果。安如等[6]利用归一化叶绿素指数法NDCI(Normalized Difference Chlorophyll Index)对比不同研究区发现,NDCI稳定性与适用性更好。
而对于中/贫营养水体的遥感反演研究,目前主要集中在光学特性较为简单的大洋等开阔性水域。由于水体清洁,内部组成成分较为单一,模型框架算法相对较为成熟。如应用SeaWiFS 数据的CZCS 算法和OC4 算法[14],以及MODIS 数据的蓝绿比值算法等。与大洋水体相比,我国大部分内陆水体光学特性较为复杂。水体组成成分除叶绿素a外,通常还包括悬浮颗粒物和有色可溶有机物。因此,这也导致内陆水体的反演算法适用性不同于大洋水体。
除此之外,部分学者也对内陆水体中/贫营养水域叶绿素a浓度反演做出了初步的探索,如:李苗等[15]对克钦湖叶绿素a浓度模型进行了对比研究,发现波段反射率比值模型Rrs(703)/Rrs(677)对克钦湖叶绿素浓度估算效果最佳。马驰等[16]利用的Landsat 7 ETM+影像对松嫩平原水体叶绿素a 含量进行估算,结果表明波段组合Rrs4/(Rrs2+Rrs3)拟合效果最好。但所使用的算法都为传统的经验模型,简单波段组合缺乏物理依据,并具有一定的随机性[5]。
参照生态部《地表水环境质量评价办法》关于湖泊富营养化评价TLI 指数法,对照单一指标叶绿素a 浓度表明,镜泊湖水体大部分处于中/贫养状态。本文基于高光谱数据,使用包括传统经验模型、半经验半分析模型在内的8种比较成熟的反演方法,通过分析不同模型的适用性来确定适合镜泊湖水域的最优模型。以期为中/贫营养内陆水域叶绿素a 浓度遥感监测提供参考模型。另外,镜泊湖不仅是该地区重要的淡水资源之一,而且位于该地区旅游景区的核心位置。近些年,由于旅游产业的不断发展和人类活动的显著增加,尤其河流上游的农业影响。镜泊湖的环境压力日益明显,湖泊生态系统的平衡也受到了严重的影响。因此,通过对镜泊湖叶绿素a遥感监测,不仅可以实时的、全面地了解其水质状况,同时也可以为镜泊湖开展水资源保护、旅游资源开发等提供重要的数据基础与理论依据。
1 数据选取与方法
1.1 野外采样及数据选取
野外叶绿素a 浓度数据获取时间为2015年9月22日和2018年7月28日。通过GPS 定位,共获取镜泊湖50 个表层水样,经过筛选剔除异常点,最后选取45 个有效采样点。其中1-30 号采样点为2015年数据,作为建模数据库; a-o 号采样点为2018年数据,作为检验数据库,具体分布如图1所示。获取的水样通过热乙醇分光光度法,测得叶绿素浓度范围为0.62~3.21µg/L,平均浓度为1.51µg/L。
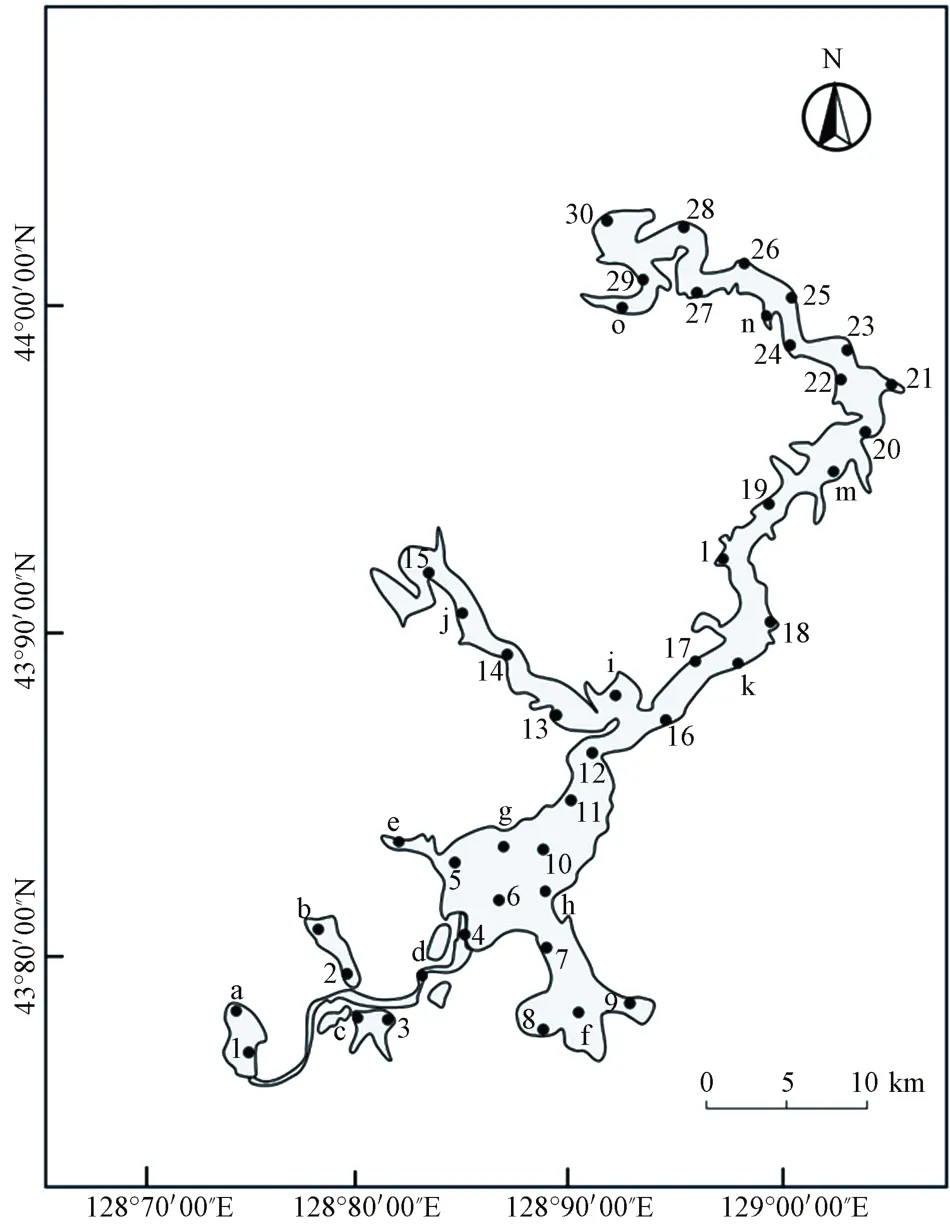
图1 镜泊湖采样点分布图Fig.1 Distribution of sample stations in Jinpo Lake
水体光谱信息获取是使用ASD Field Spec Pro FR 便携式光谱仪,其波长范围为350~1 050 nm,光谱分辨率为3 nm,光谱采集与处理参照唐军武等[17]推荐方法。
1.2 叶绿素a浓度估算模型
1.2.1 波段比值模型
波段比值模型是结合叶绿素a 光谱特征选取2 个波段的比值作为叶绿素a的反演因子,通过构建回归方程来估算叶绿素a 浓度。该模型通常使用近红外波段反射峰值与红光反射谷值的比值来估算叶绿素a 浓度,如L Han 等[18]通过分析3 个不同月份的实测数据对比发现,波段比值Rrs(705)/Rrs(670)模型稳定性较高。
1.2.2 三波段模型
三波段模型是在Gordon 等对生物光学模型研究的基础之上发展起来的,早期用来估算地表植被叶绿素含量。目前,国内外众多学者通过结合研究区不同水体特征,建立了大量水质参数的反演算法。其中,部分水域已经得到了较好的验证[19,20]。该方法原理是利用不同物质的光学特性,建立特定范围的3个波段组合与特定水质参数的相关关系,进而达到尽可能减少其他水色物质干扰的效果。三波段模型可用公式表示:
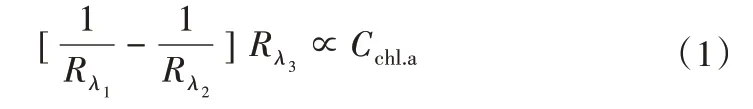
式中:Cchl.a表示叶绿素a 浓度;Rλ1和Rλ2分别代表λ1和λ2处反射率值,其中,λ1应选择在叶绿素a 反射谷附近;λ2应选择在700 nm附近的荧光峰波段。
由于此处对悬浮物和黄色物质的吸收系数与λ1位置相近,因此三波段模型可有效减轻该组分对水体吸收系数的影响。λ3所在的位置主要是用来抵消所受后向散射的影响。三波段模型的适用性较好,并具有相对较高的验证效果。但不同学者选取的3 个波段所在的实际位置并不完全一致。如Gitelson等[21]通过分析Chesapeake 浑浊水体光学特性发现,3 个波段位置分别位于675、695 和730 nm;而Dall′Olmo 等[22]通过大量的实验来确定波段位置及敏感性,研究发现λ1应设置在660~690 nm 之间、λ2应设置在700~750 nm 之间、λ3设置应大于730 nm。
1.2.3 四波段模型
在三波段模型的基础之上,Le 等[13]通过加入第4 个波段,建立了四波段模型。其目的是为了减弱浑浊水体悬浮物及纯水吸收和向后散射的影响。四波段模型一般形式如下:
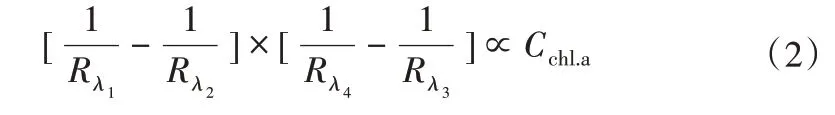
式中:λ1与λ2位置与三波段模型相同,λ3位置通常选择在720~740 nm之间,λ4位置通常选择在740~780 nm之间。具体位置可通过所建模型决定系数最优原则,迭代确定。
1.2.4 NDCI模型
NDCI 是由Maisha 等[23]提出,模型采用归一化形式,主要针对内陆水体复杂的组分而设定。模型简单实用,一般形式如下:
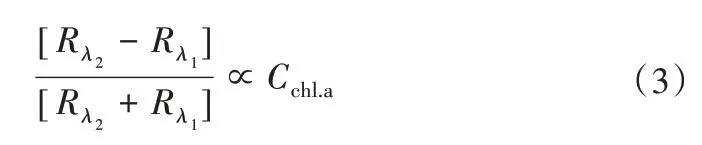
式中:Rλ1和Rλ2分别代表波段λ1与λ2处的反射率值。
为减弱其他组分的干扰,λ1与λ2应选取在叶绿素a导致光谱变化明显波段。另考虑到模型假设悬浮物与有色可溶有机物在所选位置吸收系数相等,故λ1与λ2位置差不能过大。综合考虑2种因素,λ1与λ2分别选取在675 nm 附近叶绿素a强吸收波段和700 nm附近的叶绿素强反射波段。
1.2.5 WCI模型
WCI,即叶绿素a 监测指数,是通过借鉴陆地植被叶绿素监测指数MTCI发展而来[24],模型计算公式为:
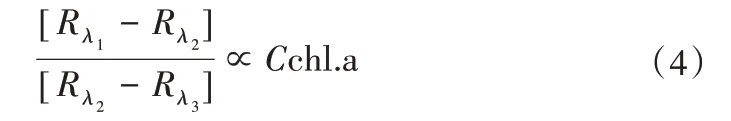
式中:Cchl.a表示叶绿素a 浓度值,λ3应选择在675 nm 附近的叶绿素强吸收波段。
由于不存在陆地植被的红边效应,λ1与λ2应尽量选择在与λ3反差较大的波段。即λ1选择在左侧650 nm左右的反射峰,λ2选择在700 nm 附近的荧光峰。具体的波段位置的确定可通过决定系数最优原则,逐步迭代确定。
1.2.6 荧光峰位置模型
荧光峰是由于植物色素的荧光效应所引起的反射锋,并且叶绿素a浓度与该反射峰的位置成正相关。因此,通常用该波段反射峰的位置来判断叶绿素a浓度。D.Zhao等[25]通过分析400~750 nm 反射光谱与叶绿素a 浓度的相关性,并发现叶绿素浓度由3 mg/L 增加到100 mg/L 时,荧光峰位置相应的从680 nm向715 nm变化,并且峰幅逐渐增加。
1.2.7 荧光峰光高度模型
水体荧光峰高度模型由Gower[26]提出,其原理是通过连接700 nm 附近荧光峰左右两侧反射谷作为基线(见图2)。计算荧光峰位置反射率值与基线高度之差,即基线荧光峰高度,公式如下:
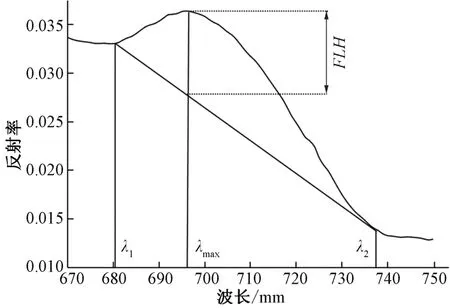
图2 基线荧光高度示意图Fig.2 Illustration of the FLH
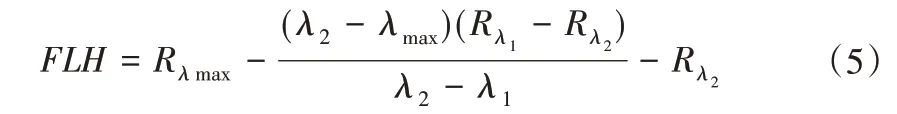
式中:FLH为荧光峰高度;λmax为是峰值波长;λ1、λ2分别为荧光峰左右两侧反射谷的波长;Rλmax、Rλ2和Rλ2分别为λmax、λ1和λ2处光谱反射率值。
1.2.8 荧光峰面积模型
对于荧光峰面积模型目前主要通过选取700 nm 附近荧光峰两侧的吸收谷来计算反射峰面积(见图3),计算公式为:
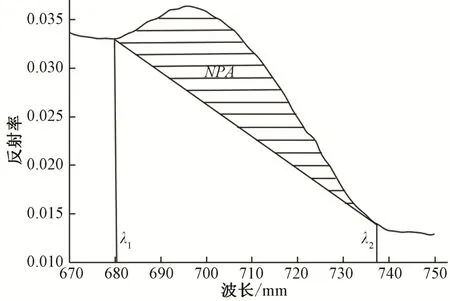
图3 叶绿素a 红波段反射峰面积示意图Fig.3 Illustration of the NPA in red band region of chlorophyll-a
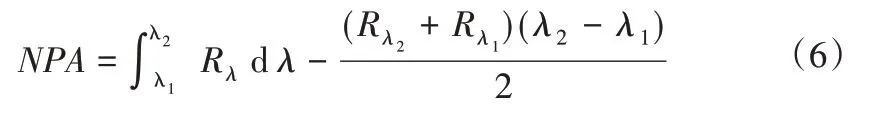
式中:NPA为叶绿素a 荧光峰面积;λ1、λ2分别为荧光峰左右两侧吸收谷的波长,nm;Rλ1、Rλ2分别为λ1和λ2处光谱反射率。
2 数据分析与讨论
2.1 镜泊湖水体光谱反射率特征
图4为本次采集的镜泊湖水体光谱反射率分布状况。可以看出,分布曲线在400~900 nm 波段范围内具有明显的内陆水体特征。其中,由于叶绿素吸收及细胞散射作用形成的反射峰出现在570~580 nm 波段;由藻蓝蛋白色素吸收形成的反射谷出现在670~680 nm 波段;由植物色素的荧光效作用形成的反射峰出现在695~705 nm 波段,该反射峰位置与叶绿素a 浓度成正相关[27]。因此,通常用该波段反射峰的位置和数值来判断叶绿素a浓度。
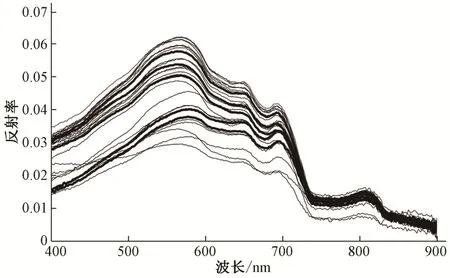
图4 镜泊湖水体光谱反射率曲线Fig.4 Remote sensing reflectance spectra of the Jinpo Lake
2.2 不同模型估算叶绿素a浓度分析
在获取的45 组实测光谱数据与同步叶绿素浓度数据中,本文利用建模数据库(2015年9月获取),使用上述8 种模型进行建模。其中波段比值模型选择荧光峰Rrs(693)与其左侧的反射率谷Rrs(680)比值;三波段和四波段模型则根据R2值最大原则,循环迭代确定最佳波段,经测试λ1、λ2、λ3分别为676、697 和740 nm,四波段λ1、λ2、λ3和λ4分别为681、693、733和766 nm。另外5种模型波段选取参考1.2所述。
在获取的样本数据(30 组)中,将以上最终确定的最优波段特征值作为自变量,同步叶绿素a数据作为因变量,通过相应算法的回归分析后,所建立的叶绿素a 浓度反演模型如表1所示。其中三波段模型拟合度最高,R2值达到0.79,优于波段比值模型的0.74,两个模型的最优回归方程都为一元二次方程,这与大多数学者研究一致[28,29];NDCI 模型和四波段模型的最优模型也为一元二次方程,R2值也分别达到了0.74 和0.69;荧光峰位置模型、光峰高度模型和荧光峰面积模型R2值也达到了0.6 左右,与多数学者观点一致,最优回归方程为指数方程[11,24,29];WCI 模型是本次所选模型中决定系数相对较低的模型,R2值为0.51,但也可以明显地表现出叶绿素a 浓度与光谱值之间的相关性。

表1 不同方法叶绿素a反演模型Tab.1 Chlorophyll-a retrieval model in different methods
使用验证数据库(2018年7月获取)对上述8 种叶绿素a浓度模型的反演精度进行评价。结果见图5。
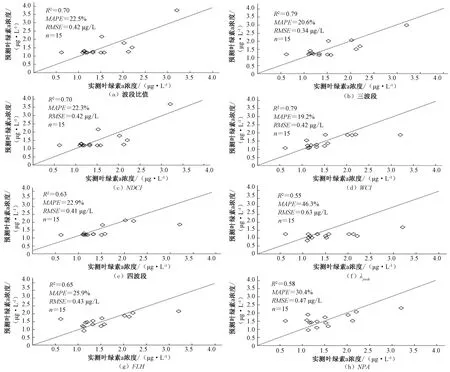
图5 叶绿素a 浓度估算值与实测值的对比Fig.5 Comparison between measured and estimated the chlorophyll-a concentration
可以看出,上述8种方法都能在一定程度上反演出镜泊湖水体的叶绿素a 浓度状况(MAPE为20.6%~46.3%,RMSE 为0.34~0.63 µg/L)。但在不同营养状况的水域,由于水体光学特性的差异,模型适用性有所不同[29]。在本研究区,镜泊湖属于中营养/贫营养水域。检验结果显示,与其他模型相比,三波段模型效果最好,RMSE与MAPE分别为0.34µg/L和20.6%。
三波段模型和四波段模型都是基于内陆水体复杂的组成成分和光谱特性所构建的。模型中波段的选择范围位于红外与近红外波段之间,其中λ1与λ2分别选取在叶绿素a反射谷与荧光峰波段。由于两处悬浮物和有色可溶性有机物的吸收系数相近,因此模型可在一定程度消除两种物质对水体光谱的影响。同时,λ3的加入也可以部分抵消水体后向散射的影响[26]。但是由于不同水域水体组成成分不同,所呈现的光谱特征也往往不同,因而建模的最佳波段具有一定的不固定性。在此基础之上,四波段模型通过加入第4个波段来进一步减弱浑浊水体悬浮物及纯水吸收和后向散射的影响。但本研究四波段模型MAPE为22.9%,RMSE为0.41µg/L,均低于三波段模型的检验效果。其原因一方面,可能是由于镜泊湖水体组成成分和光学特性在时间上与空间上差异较大,当悬浮物在所选波段的吸收系数差异较大时,增加近红外波段的四波段模型也可能带来一定干扰,从而无法改善模型的效果[29]。另外,在近红外区域,三波段模型是以悬浮物颗粒远小于纯水吸收系数为前提,而在高浑浊水域,近红外波段的吸收和散射并不能被忽略,四波段模型也正是基于此改进模型的精度[13]。但镜泊湖水体并非高浑浊水体,因此,加入的第四波段也可能对模型产生一定的干扰。
在NDCI 模型的验证中,RMSE为0.42 µg/L,MAPE为22.3%。由于模型的波段选择与波段比值一致(700 nm 左右反射锋与叶绿素吸收峰),因此反演效果与波段比值模型也比较接近,并没有优于三波段模型。这与安如等[6]对太湖的反演模型结论一致,即NDCI法较适用于叶绿素浓度较高的湖泊水质监测,对于中营养/贫营养状况的镜泊湖反演效果并没有较大的提升。WCI 模型虽拟合效果不高,但在模型验证中,平均相对误差MAPE却达到19.2%。一方面可能是由于本次采集样本数量较少,建模数据的选取也会影响模型的精度;另一方面WCI 模型是在陆地植被叶绿素a 监测模型MTCI 的基础上,通过波段差值的比值来增大叶绿素a 吸收和反射的差异。该研究区具有较高叶绿素a浓度,通过波段的处理,水体叶绿素a特征更加明显[24]。而本研究区属于中营养/贫营养水域,叶绿素a浓度相对较低,通过该模型的波段变换并没有改善叶绿素a 浓度的反演精度。这也体现了在不同类型水体中,模型通用性不确定的特点[2,5,7]。
荧光峰位置模型、荧光峰高度模型和荧光峰面积模型已经被很多学者证明过可以作为反演叶绿素a浓度的传统经验模型[11,24,29]。对比该3 种反演模型的检验效果,荧光峰高度模型与荧光峰面积模型比较稳定,反演精度差别不大,RMSE分别为0.43 和0.47µg/L,MAPE分别为25.9%与30.4%。而荧光峰位置模型的验证精度则相对较低,RMSE为0.63 µg/L,MAPE为46.3%。其主要原因可能为此次采样湖泊水体叶绿素浓度普遍偏低,浓度跨度较小导致建模数据荧光峰位置比较接近,甚至相同,从而影响模型精度。
3 结论
本文结合2015年9月和2018年7月实测光谱数据,对镜泊湖叶绿素a 浓度反演模型的精度进行了评估。以期为中营养/贫营养内陆湖泊的最佳反演模型提供一定的数据支撑。具体结论如下:
(1)在所构建的8种模型中,三波段模型是最适用于中营养/贫营养状况的镜泊湖叶绿素a 浓度估算模型,模型R2值为0.79,MAPE为20.6%,RMSE为0.34µg/L。模型可表示为y=2 864.3x2-107.43x+2.14,x=[Rrs-1(676)-Rrs-1(697)]×Rrs-1(740)。
(2)与三波段模型对比研究发现,在低叶绿素浓度及低浑浊水体中,增加近红外波段的四波段模型也可能带来一定的不确定性,从而降低反演精度,但仍需更多水体样来进一步验证。
(3)WCI 模型的R2值较低,但在模型验证中,MAPE却只有19.2%。是否与中营养/贫营养湖泊叶绿素a浓度较低有关仍需要进一步验证。
(4)对于叶绿素a浓度跨度较小的镜泊湖水域,半经验半分析模型建模精度优于传统的经验模型(如: 荧光峰位置模型、荧光峰高度模型和荧光峰面积模型)。

