应用神经网络动态估计信号交叉口饱和流率

(1.清华大学 土木水利学院， 北京 100084；2.清华大学 交通研究所， 北京 100084；3.北京工业大学 北京市交通工程重点实验室， 北京 100124；4.北京建筑大学 土木与交通工程学院， 北京 100044)

0 引言

饱和流率是通行能力中重要的参数，是指在连续绿灯时间内，进口道上连续车队通过停车线的最大流率[1]。饱和流率是计算通行能力、评价交叉口服务水平和信号配时的重要参数。目前，获得饱和流率常用的方法有2种，一种是模型法，一种是实测法。

国内外对于饱和流率的研究主要集中在饱和流率计算模型以及实测方法两个方面。在饱和流率计算模型方面，国内外学者[2-9]主要分析了本地交通特点，通过实测数据，将常见的修正系数如车道宽度、进口道坡度等进行本地化改进，针对一些特殊影响因素如公交停靠站、导流标线等构建新的修正系数计算模型。在实测方法方面，美国道路通行能力手册(highway capacity manual, HCM)[10]、别一鸣等[1,11]主要集中在车辆饱和状态的判别，通过动态采集饱和流率实时掌握通行能力变化，为交通控制方案制定提供支持。但就饱和流率计算模型而言，影响饱和流率的因素很多，直接从理论上推导某种规律来描述饱和流率是无法完全涵盖的，难以通过传统统计准确表达。就实测方法而言，无法掌握饱和流率变化与交叉口各交通特征之间的关系，对于拥堵难以准确发现其原因并实现精细化改进。因此，构建既能准确描述饱和流率与各影响因素之间关系，又能掌握饱和流率实时动态变化特征的模型，显得十分必要。

考虑到神经网络与传统统计学方法不同，在无先验模型基础上，通过训练学习，自动生成输入与输出的关系表达，能够描述任意复杂的系统。通过神经网络模型研究饱和流率成为可能。本文基于实测数据，提出了基于神经网络的饱和流率估算方法，并与经典的HCM方法对比分析。本文研究成果对于提高饱和流率估算准确性，动态的交通控制方案调整，精细化的交通运行管理具有重要意义。

1 饱和流率估算方法

信号交叉口各进口道的实际饱和流率是由车道组饱和流率叠加而成。因为，进口道饱和流率是随车道数和渠化方案变化而变化。换言之，计算某一条进口道饱和流率需要计算每个车道实际饱和流率，并进行累加。各车道饱和流率可以通过饱和车头时距换算得到如公式(1)，也可通过对基准饱和流率进行一系列修正得到如公式(2)。

(1)

(2)

式中，ht为实测饱和车头时距；S为实际饱和流率；S0为基本饱和流率；fi为不同交通条件、几何条件等对应的修正系数。在实际研究中，饱和车头时距通过人工调查或者采集设备获得，经过公式(1)计算可得饱和流率。无法进行数据采集的交叉口，如规划某交叉口，可通过公式(2)计算获得饱和流率。国家标准《城市道路交叉口规划规范》(GB 50647—2011)[12]也是借鉴公式(2)模型。其关键是确定影响饱和流率因素的修正系数。

1.1 饱和流率影响因素分析

HCM手册第18章[10]列举了影响饱和流率代表性因素，共有11类，分别为车道宽度、大车比例、进口道坡度、路内停车情况、公交停靠站、地区类型、车道利用(多车道交通量分布不均)、左转交通、右转交通、行人与非机动车。每个因素对应的调整系数都是该因素与饱和流率的独立关系表达。如果按照每个周期影响因素的变化情况分，大致可以将其分为动态因素与静态因素。其中，静态因素为车道宽度、进口道坡度、地区类型，其余为动态因素。由此可知，饱和流率并非恒定，而是会随着动态因素的变化而变化。同样，11类的影响因素也无法完全涵盖所有交通特征。HCM手册中11类影响因素主要适用于美国地区交通情况。而在印度这样的发展中国家，交通流组成中两轮摩托车的比例较高，两轮车的车长与性能与小客车有着明显差异，将会直接影响实际饱和流率[13]。同样在中国，由于用地空间限制，交叉口形成短车道，由短车道长度不足引发车辆排队溢出等现象导致饱和流率的变化[14]。但上述交通情况均未在HCM手册中体现。

总体来说，车道饱和流率的影响因素众多，不同车道类型(专用、共用)、不同信号类型(左转时的许可型、保护型)所需要考虑的影响因素也不相同，一些特殊的交通特性也会导致饱和流率的变化。目前，通常做法是，分析新的影响因素与饱和流率的单独关系，建立回归模型[15]，推导形成新的修正系数。但在实际研究过程中发现，控制变量，获得单一因素与饱和流率的直接关系较为困难。实测数据中往往会存在多因素之间的交织。如图1 所示，作者在北京地区实地采集了不同车道宽度、不同大车比例下直行车道的饱和流率，其中“m”为实测直行车道饱和流率，“hcm”为模型对应预测饱和流率。由图1可知，只考虑车道宽度和大车影响下，实际饱和流率的变化与模型计算不符，在窄车道大车比例高的情况下，实际饱和流率下降更加明显，说明车道宽度和大车比例因素间存在着一定交互影响。这也进一步说明，当前HCM模型无法完全表达出各种因素之间的复杂关系。

图1 饱和流率预测值与实测值对比Fig.1 Comparison between predicted and measured values of saturation flow rate

1.2 饱和流率神经网络预测方法

交叉口饱和流率受各种因素的影响，无法直接找到影响的参数与实际饱和流率之间准确的函数表达，而是通过采用单一参数与饱和流率之间的关系构建修正系数，并通过乘积方式对基本饱和流率进行累积，达到预测实际饱和流率的目的。但这种方法往往受随机因素，以及因素之间的交互关系表达不足的影响，无法准确预测实际饱和流率。根据神经网络方法的特点可知，通过神经网络构建的数学模型，经过训练可以很好的表达输入与输出参数的映射关系，无需寻找因素之间的复杂非线性关系。所以本文拟构建基于神经网络的饱和流率动态估计方法。

首先，需要获取相关数据，由于饱和流率是信号配时的关键参数，实时获得饱和流率显得十分重要。饱和流率与交通量特性不同，交通量以5 mim或15 min间隔进行实时统计；而由饱和流率定义可知：“在信号灯连续显示绿灯时间，进口道上一列连续车队通过停止线的最大流率”，其与信号周期相关，采用每个信号周期为统计间隔比较合适。根据神经网络模型特点，需要确定输入与输出参数，本文输入参数是饱和流率影响因素，输出参数是对应的实际饱和流率。对于输出参数而言，可通过在进口道处设置的检测器获得，获得方法借鉴文献[9]，具体步骤如下：①先判断红灯期间排队车辆数是否超过7 veh，如果少于7 veh说明未达到饱和状态，无法直接获得饱和车头时距，不进入提取，否则继续；②判断第4辆车至排队末尾车辆是否为饱和车头时距；③提取当前周期第4辆车到处于饱和状态的最后一辆车的平均饱和车头时距；④根据公式(1)计算饱和流率。对于输入参数而言，主要分为两类，一类是静态参数，一类为动态参数，通过不同方式获得。常见的静态参数为车道功能、宽度、坡度、地区类型等，可以通过人工采集，更新频率为一年或视情况而定。而常见的动态参数为车辆组成(不同车型比例)，左右转车辆比例，行人与非机动车流量等，数据获取采用进口道设置的检测器获得。其次，确定神经网络结构，目前主要思路是通过当下静态与动态参数来预测实际饱和流率。故神经网络的结构主要是，输入层面节点个数为影响具体车道的动静态因素个数；输出层节点个数为1，输出变量为实际饱和流率；隐含层节点个数参考经验公式[16]或者分析选取，常见的公式如下：

(3)

式中,n为输入单元数，m为输出神经元数，a为取值1到10之间的常数。本文结合公式(3)确定隐含层神经元节点数区间，并通过实验测试获得预测误差，以预测误差最小确定最佳隐含层神经元节点数。同样，根据实验选取适合的激活函数、梯度下降函数以及学习速率等参数。最后，神经网络结构确定后，通过部分数据对网络进行训练验证，可以获得用以预测的神经网络模型。考虑网络训练可能需要时间，可以隔一段时间重新对网络进行训练优化。

本文采用神经网络方法预测饱和流率总结可分为以下5个步骤：

Step 1：根据实际情况分析影响当前车道饱和流率的因素，确定输入参数。

Step 2：根据Step1中相关参数，确定神经网络结构，如隐含层神经元个数，激活函数，梯度下降函数，学习速率等参数。

Step 3：选取部分历史数据作为训练集，启动神经网络进行训练优化，经迭代直至收敛，获得神经网络模型。并通过另一部分历史数据进行验证，验证通过后，保存当前神经网络模型参数，各层间的权重矩阵与偏差矩阵。

Step 4：利用训练好的神经网络模型和检测器当前周期相关数据，滚动式预测下一周期饱和流率。

Step 5：判断是否达到网络训练更新时间间隔，如满足转到Step 3，否则转至Step 4。

2 算例分析

为了证明本文提出模型的有效性与可靠性，选取不同复杂程度的交通场景，基于实测数据构建估计饱和流率的神经网络模型、HCM模型并对模型进行对比分析。由交通流运行特征可知，在不同类型车道上，车流所受的影响因素也有所区别。因此，在选择交通场景时应充分考虑交通流特征和影响因素的多少，最终选取了进口道为直行、直左、直右车道的3种场景。其中，场景1(直行车道)位于北京市丰台区石榴庄路与榴乡路交叉口，该交叉口北接南三环，南接南四环与德贤路，高峰时段交通量巨大；场景2(直右车道)位于北京市海淀区车公庄西路与首都体育馆南路交叉口，附近有白石桥南地铁口，行人和非机动车流量较大；场景3(直左车道)位于北京市东城区安定门外大街与外馆斜街交叉口，周围均是居住小区，行人流量较大。

2.1 数据获取

三种场景所在的交叉口是位于北京市中心的信号控制型交叉口，具体渠化如图2所示。各交叉口进口道详细的几何特征和信号配时方案如下：

场景1(直行车道)，石榴庄路与榴乡路交叉口是主干路和次干路相交，南北方道路是主干道，其中，南进口车道为2条左转专用车道，4条直行车道，1条右转专用车道，北进口车道为1条掉头车道，1条左转专用车道，5条直行车道，1条右转专用车道。高峰时段，信号配时方案为4相位，右转车辆不受灯控，左转车辆与直行车辆分开放行，周期时长140 s，直行相位的黄灯时长4 s，左转相位的黄灯时长3 s，所有相位全红时长2 s。南北直行绿灯时长44 s，南北左转绿灯时长15 s，东西直行绿灯时长42 s，东西左转绿灯时长17 s。选取的是北进口与南进口9条直行车道进行分析。

场景2(直右车道)，车公庄西路与首都体育馆南路交叉口是两条主干路相交，其中，东进口车道为1条左转专用道，2条直行车道，1条直行右转车道，1条右转专用车道。高峰时段，信号配时方案同样为4相位，周期时长148 s，所有黄灯时长为3 s，全红时长为2 s，东西直行绿灯时长40 s，东西左转绿灯时长20 s。选取的是东进口1条直右车道分析。

场景3(直左车道)，安定门外大家与外馆斜街交叉口是主干路和支路相交，东西方向为支路，其中，西进口车道为1条直左车道，1条右转专用道。高峰时段，信号配时方案为3相位，周期时长156 s，所有黄灯时间为3 s，全红时间为2 s，东西直行兼左转绿灯时长42 s。选取的是西进口1条直左车道分析。

(a) 场景1交叉口

(b) 场景2交叉口

(c) 场景3交叉口

在3种场景中，饱和流率受到的影响是不同的。图3展示了交叉口使用者争夺冲突空间的示例，进一步说明了各影响因素特征。以直行车道为例，饱和流率受到的影响因素较少，主要受车队内车辆组成影响。但在调查中发现，在多直行车道时，经常发生车辆之间相互干扰，车辆驶离停车线后自由选择出口道位置，会影响后车的平稳运行导致饱和流率的变化，实际干扰情况如图4所示。以直右车道为例，当绿灯亮起时，直行和右转车辆均可通过停车线，因此，饱和流率不仅受车队内车辆组成影响，也会受右转车辆比例影响；当右转车辆到达相交道路出口道时，也会受过街的行人与非机动车的干扰。以直左车道为例，同直右车道相同，也会受到左转比例，行人与非机动车的干扰；但不同的是，绿灯亮起时对向直行车辆也会通过，左转车辆行驶过程中也会受到对向直行车辆干扰造成饱和流率变化。

图3 信号交叉口常见的冲突位置Fig.3 Common conflict zones of signalized intersections

图4 多进口直行车道车辆之间相互干扰情况Fig.4 Interference between vehicles at multiple through approaches

鉴于涉及到数据较多，本文采用视频摄像的方法记录交叉口车辆运行，并通过人工提取方式获得车头时距数据以及相关影响因素数据。使用滚轮仪记录进口道车道宽度以及其他几何特征。使用秒表记录信号周期、相位等信息。为便于分析，在提取过程中，以周期为记录单元，记录每个周期影响因素和对应的饱和车头时距。直行车道主要记录大车比例、车道的宽度、受到邻侧车道影响(受到影响记录1，未受影响记录0)，采集时间主要集中在2019年4月2日至4月4日晚高峰(17:30—19:30)，9条直行车道共采集了420个周期数据。直右车道主要记录大车比例、右转比例、行人有效流率、非机动车有效流率。直左车道主要记录大车比例、左转比例、行人有效流率、非机动车有效流率、对向直行车辆有效流率。采集时间集中在2018年6月12日至6月14日晚高峰(17:30—19:30)，直右和直左车道分别都采集了90个周期数据。

2.2 模型构建与标定

以3层神经网络为基础，结合影响饱和流率的因素数据，进行模型的输入层、隐含层、输出层的参数设计，选取合适的隐含层节点数、激活函数、梯度下降函数、学习速率，以输出结果误差最小为目标，形成饱和流率估算模型。本文所使用的神经网络程序采用由Google开发的TensorFlow开源软件库实现。该软件库有规范化的神经网络架构，且内置多种函数，便于代码编写。同时，通过TensorBoard将计算流程及结果可视化，使得程序优化调试更加容易理解，其界面如图5所示。

图5 TensorBoard 界面Fig.5 TensorBoard interface

首先，要确定输入与输出变量。一般情况下，影响因素作为输入变量，实际饱和流率作为输出变量。根据上节数据获取情况可知，不同场景下实测数据中饱和流率的影响因素不同，即不同场景下输入变量有所差异，输出变量均为实际饱和流率。场景1(直行车道)：3个输入变量分别为车道宽度、车辆组成、多车道横向干扰。场景2(直右车道)：4个输入变量分别为车辆组成、右转比例、行人有效流率、非机动车有效流率。场景3(直左车道)：由于观测时间内没有大型车通过，大车比例每个周期均为0，所以输入变量也为4个分别为右转比例、行人有效流率、非机动车有效流率、对向直行车流率。其次，划分训练集与测试集，场景1选取300个周期数据作为训练集，剩余120个周期数据作为测试集；场景2和场景3均选取65个周期数据作为训练集，剩余25个周期作为测试集。然后，标定神经网络模型中的超参数并保存参数权重和偏差矩阵。在TensorFlow中，可调节的超参数主要有隐含层数、隐含层节点数、激活函数、学习速率、梯度下降函数。其中，由于输入参数较少，一般情况下隐含层数选择为1层，本文同样选择1层。其他超参数的标定过程如下：

Step 1：确定超参数的变量范围。如隐含层节点个数范围，可根据公式(3)计算，大致范围在3至12之间，常见激活函数6种，学习速率一般在0.01到0.1之间，常见梯度下降函数有6种。

Step 2：控制超参数变量，进行训练与测试。如需要确定隐含层节点数，其他参数选择默认值，隐含层节点数从3到12，依次进行训练，保存神经网络结构与模型参数，利用同样的结构和参数带入测试集，获得预测的平均绝对误差(mean absolute error， MAE)和平均绝对百分比误差(mean absolute percentage error， MAPE)。

Step 3：对比模型预测误差，确定超参数变量。针对不同实验，对比测试集中模型的预测误差，选取误差最小时超参数变量作为模型标定变量。

以场景1构建的模型为例，采用上述步骤，确定的神经网络参数，具体结果如图6所示。其中，隐含层节点数为12，激活函数为sigmoid，学习速率为0.04，梯度下降函数为RMSPropOptimizer。同理，场景2与场景3确定与场景1相似，不再赘述，具体结果见表1。就神经网络模型标定而言，在实际使用中可通过编程实现各超参数的自动选择，省去人工标定的繁琐过程。

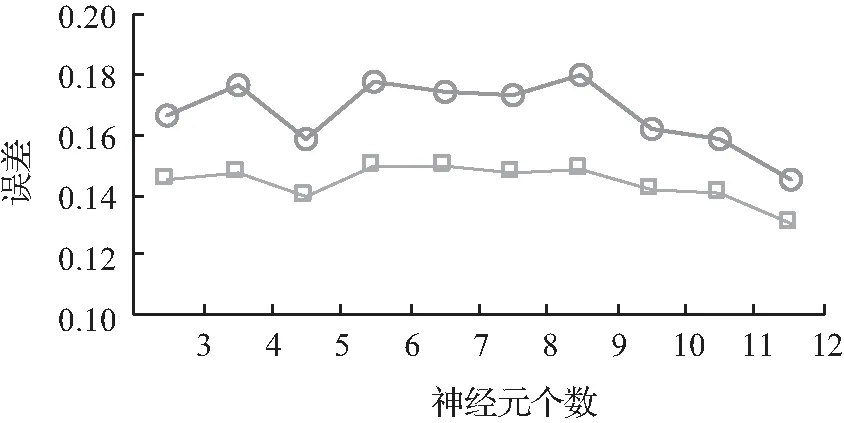
(a) 神经元个数确定

(b) 激活函数确定

(c) 学习速率确定

(d) 梯度下降函数确定

图6 神经元网络模型超参数确定Fig.6 Determining the hyperparameters of neural network models

表1 三种交通场景的神经网络模型超参数标定结果Tab.1 Calibration of hyperparameters for neural network models at 3 scenarios

所有超参数确定后，将3种场景的训练集数据分别代入模型进行训练，训练完成后，保存模型权重与偏差矩阵参数，将测试集数据导入训练好的模型中，进一步查看模型预测结果。场景1，2，3模型中，输入层与隐含层之间的权重矩阵如下。

场景1的模型中，输入层与隐含层之间的权重矩阵W11和偏差矩阵b11如下：

隐含层与输出层之间的权重矩阵W12和偏差矩阵b12如下：

b12=[0.476]。

同理，场景2模型的参数W21,b21,W22,b22如下：

b22=[-0.089]。

同理，场景3模型的参数W31,b31,W32,b32如下：

b32=[-0.102]。

3种场景模型的训练集和测试集预测结果如图7所示。训练集和测试集中预测值和实测值较为吻合，根据计算MAPE值，场景1训练集为0.06(准确率则为94%)，测试集为0.11(准确率为89%)，场景2训练集为0.07(准确率则为93%)，测试集为0.07(准确率为93%)，场景3训练集为0.04(准确率则为96%)，测试集为0.05(准确率为95%)，这说明该方法能够较为准确的估计饱和流率。

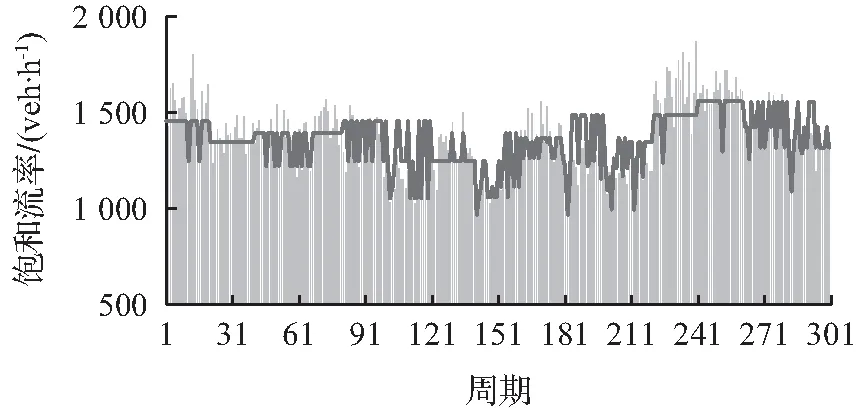
(a) 场景1直行车道训练集

(b) 场景1直行车道测试集

(c) 场景2直右车道训练集

(d) 场景2直右车道测试集

(e) 场景3直左车道训练集

(f) 场景3直左车道测试集

图7 饱和流率预测结果与实测数据对比Fig.7 Comparison between predicted and measured results

2.3 对比分析

为了进一步验证本文所提出方法的有效性，对采集的数据同时采用HCM方法和传统统计学方法进行计算，将结果进行对比分析。场景1中影响饱和流率的因素还包含有多车道横向干扰因素，而该因素在HCM方法中并未体现，因此可以采用统计学方法进行计算。常用的有两种，第一种是寻找该因素与饱和流率之间的关系，经过推导得出该因素对应的修正系数，然后纳入HCM乘法方程计算，该方法适用于单一因素与饱和流率之间的关系容易确定的情况，在无法剥离单一因素时，该方法会出现一定偏差。HCM方法中，重点需要确定两类参数，一是基本饱和流率，二是各影响因素对应的修正系数。为了使估算饱和流率更符合实际的交通运行特征，将基本饱和流率、车道宽度修正系数、重车率修正系数采用《城市道路交叉口规划规范》(GB 50647—2011)中给定的推荐值。左转修正系数、右转修正系数、行人和自行车修正系数国标中未给出，本文采用美国通行能力手册中的计算方法，此处不再赘述。基于3个场景的测试集数据，分别采用训练好的神经网络模型，以及确定好参数的HCM模型对饱和流率进行估算。并计算每个周期估算值的误差，形成误差分布，具体如图8所示。

(a) 场景1各模型估算误差分布

(b) 场景2各模型估算误差分布

(c) 场景3各模型估算误差分布

(d) 各模型估算的MAPE对比

图8 HCM与神经网络模型估计精度对比Fig.8 Comparison of the predicted accuracy with HCM, Neural Network methods

两种模型的估计饱和流率的平均绝对值百分比误差在场景1中分别为29.30%，11.23%，场景2中分别为21.60%， 7.02%，场景3中分别为24.53%， 4.70%。由此可知，神经网络模型均优于HCM模型。进一步分析，随着场景复杂程度的提升，HCM模型精度明显提升，尤其在场景2与场景3中，饱和流率受到的影响因素较多，除受自身(本车队)内部干扰还会受到外部(行人与非机动车)其他交通参与者干扰，此时神经网络优势明显。

3 结论

本文将信号交叉口进口道饱和流率以周期为单位统计，同时记录相关影响因素，按时间序列进行排列，采用神经网络的方法动态实时计算饱和流率，通过与HCM模型对比可以得到如下结论：

① 影响饱和流率的因素较多，有静态因素有动态因素，因此饱和流率并非恒定，而是随交通条件变化而不断变化。

② HCM只给出了基本影响因素，缺少特有交通特性下的影响因素，且因素之间的复杂关系难以用传统统计学方法表达，神经网络可以用来描述多影响因素与饱和流率之间的关系。

③ 与HCM方法相比，交通场景越复杂影响因素越多，神经网络模型的优势愈加明显，在直左和直右进口道场景下，神经网络模型预测误差更小，平均误差分别为7.02%，4.70%。

本文提出的动态估计饱和流率的方法是在能够动态获取影响因素基础上实现，在实际应用过程中，还需将模型构建与标定过程实现自动化，并通过与信号配时系统连接，进一步达到精细化交通管理与控制的目标。