基于排序学习的连续兴趣点推荐

(1.广西中医药大学 校长办公室、发展规划处、网络和信息化管理办公室(合署), 广西 南宁 5302002.中国人民大学 信息学院， 北京 100872；3.广西师范大学 计算机科学与信息工程学院， 广西 桂林 541004)

0 引言

随着Web 2.0的发展和带有定位功能设备的普及，位置社交网络应运而生并得到快速发展，如Foursquare、Facebook Places和街旁等[1]。用户可以在位置社交网络中对兴趣点(point-of-interest, POI)(如商场、餐馆等)进行签到，并在线分享自己在物理世界中的体验。位置社交网络将线上虚拟世界和线下物理世界有机结合在一起，使得用户可以在任何时间、任何地点获取和分享位置信息。同时，随着城市的快速发展，兴趣点数量迅速增加，使得用户难以从海量的兴趣点中找到自己感兴趣的兴趣点，用户将会面临信息过载问题。兴趣点推荐旨在向用户推荐符合其兴趣偏好的兴趣点，这已经成为一项重要的位置服务，得到了学术界和工业界的广泛关注[2]。

当前兴趣点推荐研究[3]把用户所有的签到记录看成一个整体，这种方法只考虑了用户与兴趣点之间的签到关系，忽视了用户连续签到的兴趣点之间的关系。实际上，用户当前所处的兴趣点与下一个要访问的兴趣点之间具有很强的关联性，例如用户晚饭之后一般会去公园散步，而不是去公司上班。这种签到行为的序列模式[4]是兴趣点推荐任务中要考虑的重要因素，在向用户推荐兴趣点时要根据其当前所在的兴趣点，在此情况下，兴趣点推荐的任务是根据用户当前所处的兴趣点为其推荐下一个要访问的兴趣点，即连续兴趣点推荐。连续兴趣点推荐不仅可以帮助用户探索新世界，还可以帮助广告商对潜在客户进行精准营销。

由于位置社交网络是一种包含用户与用户之间关系、用户与兴趣点之间关系、兴趣点与兴趣点之间关系的复杂异构网络[5]，与传统推荐系统相比，连续兴趣点推荐系统面临一些新的挑战。

① 用户的个性化偏好。LBSNs中用户的个性化偏好主要表现在两个方面：一是伴随时间和地理位置的变化，用户偏好也在变化，例如，有的用户早晨喝完咖啡去逛街，有的用户早晨吃完饭去上班；二是具有相似兴趣偏好的用户也可能会有不同的行为模式，例如有的运动爱好者喜欢去公园跑步，有的运动爱好者喜欢去健身房锻炼。因此，连续兴趣点推荐系统应根据用户的个性化偏好，为用户推荐符合其个性化偏好的兴趣点。

② 数据稀疏性。签到行为是用户的自主性行为，用户只在一部分访问过的兴趣点上进行签到，导致签到数据极度稀疏。此外，位置社交网络中有成千上万个兴趣点，用户只可能去数量有限的兴趣点，这同样导致签到数据十分稀疏。

③ 签到行为的隐式反馈属性。与传统推荐系统中用户通过评分表达显式反馈不同，用户在兴趣点上的签到行为是一种隐式反馈，签到过的兴趣点仅代表用户访问过该兴趣点，无法反映用户对该兴趣点的满意程序，未签到过的兴趣点分为确实不感兴趣的兴趣点和尚未发现但感兴趣的兴趣点。这导致签到数据中仅有用户在签到过的兴趣点之间的转移记录，即观察到的转移记录，缺少签到过的兴趣点与未签到过的兴趣点之间、未签到过的兴趣点之间的转移记录，即未观察到的转移记录。

针对上述挑战，本文提出一种基于排序学习的连续兴趣点推荐模型，该模型使用排序学习算法优化求解模型参数，提升了推荐系统的性能。具体而言，首先，将用户的连续签到行为建模为用户-当前兴趣点-下一个兴趣点的三阶张量，利用张量分解模型对三阶张量进行分解，并拟合用户访问兴趣点的个性化偏好。然后，根据用户在物理世界中活动范围有限，更加倾向于选择距离较近的兴趣点，假设用户对兴趣点的偏好程度，与相距的地理距离成反比，据此定义用户访问兴趣点的地理距离偏好，作为衡量用户对兴趣点偏好程度的因素，有效缓解了数据稀疏性问题。最后，针对签到行为的隐式反馈属性，将观察到的转移记录按照转移频率排序，并与未观察到的转移记录一起组成样本列表，以样本列表作为训练实例，根据用户关注的是兴趣点对应的排名，而非真实的转移概率值，将兴趣点推荐任务建模成对兴趣点的排序任务，采用基于排序学习的标准优化目标方程，将排名在前N位的兴趣点推荐给用户。

1 相关工作

1.1 兴趣点推荐

兴趣点推荐系统通过分析用户的历史签到数据，得到用户偏好和行为规律，并结合兴趣点的属性信息，向用户推荐满足个性化偏好的兴趣点。兴趣点推荐系统已经成为位置社交网络中的热门研究课题，得到了学术界和工业界的广泛关注。结合经典推荐系统的分类方法，本文将近年来的连续兴趣点推荐研究工作分为两类：

第一类是基于内存的协同过滤推荐算法。该类方法首先找到与目标用户具有相似兴趣偏好的用户群体，将相似用户访问过的兴趣点推荐给目标用户，或者是找到与目标用户访问过的兴趣点相似的兴趣点，将相似兴趣点推荐给目标用户。YE等[6]分析了用户签到记录的地理分布情况，提出了融合地理信息的协同过滤推荐模型，该模型根据历史签到数据计算用户之间的相似度，找到与目标用户相似的用户，把相似用户访问过的兴趣点推荐给目标用户。

第二类是基于模型的协同过滤推荐算法。该类方法利用矩阵分解、深度学习等机器学习算法，基于签到数据构建推荐模型，用训练完成的推荐模型计算用户对兴趣点的偏好程度，将满意度高的兴趣点推荐给用户。彭宏伟等[7]提出了基于上下文感知的兴趣点推荐算法，该算法使用矩阵分解模型来融合地理信息、社交影响等LBSNs中的上下文信息，克服了数据稀疏性、个性化推荐等挑战，并且时间复杂度较低、可扩展性较好。

在位置社交网络中，用户访问兴趣点的概率受到多种情景因素(如时间、兴趣点分类等)影响，导致兴趣点推荐需要考虑多种复杂的因素。随着情景因素的增多，当前许多研究工作试图融合各种情景因素来提升兴趣点推荐系统的性能。CHENG等[4]提出了基于局部区域的张量分解模型，该模型通过融合用户从当前兴趣点移动到下一个兴趣点的地理距离信息，为用户提供准确高效的连续兴趣点推荐服务。高榕等[8]利用矩阵分解技术将多种异构数据融合到统一的模型中，通过融合LBSNs中的内容信息、地理信息和社交关系等，准确高效地建模了用户的兴趣偏好，提高了兴趣点推荐的准确率和召回率。LI等[9]研究了用户受时间信息、地理信息等多种情景因素影响的兴趣点推荐，由于用户在不同情景因素组合中会表现出不同的行为模式，将个性化的马尔科夫链与行为模式相结合，提出了基于潜在行为模式的连续兴趣点推荐模型。

1.2 排序学习

排序学习最早应用于信息检索领域，使用训练实例构建排序模型，结合机器学习思想，迭代优化模型参数，用训练完成的排序模型进行推荐[10]。按照输入训练实例的不同，可以将排序学习算法分为三类：点级排序学习算法(point-wise)、对级排序学习算法(pair-wise)和列表级排序学习算法(list-wise)。

点级排序学习算法将单个项目作为训练实例，以单个项目的特征作为评分标准，未考虑项目之间的排序关系，将排序问题转化为回归问题[11]。对级排序学习算法将项目对作为训练实例，构建项目对之间的偏序关系，利用支持向量机、人工神经网络等机器学习算法构建排序模型，用于判断任意两个项目的偏序关系是否合理，将排序问题转化为二分类问题[12]。列表级排序学习算法将项目列表作为训练实例，直接对项目列表进行优化，构造损失函数以度量预测排序与正确排序之间的相似度，迭代求解排序模型参数[13]，如rank-net[14]和rank-cosine[13]等，或者将排序问题转化为最优化问题，定义最优的排序结果会得到最好的评价标准，直接优化项目列表的排序，如ListMLE[14]等。

2 用户连续签到行为建模

2.1 问题描述

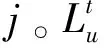
2.2 连续签到行为建模

位置社交网络中的历史签到数据是用户u从当前兴趣点i转移到下一个兴趣点j的转移记录，可以把用户、当前兴趣点和下一个兴趣点组成三阶张量χ，即χ∈[0，1]|U|×|L|×|L|，张量中的非零元素χu,i,j表示观察到的转移记录。

3 基于排序学习的连续兴趣点推荐

本文提出的连续兴趣点推荐模型首先计算用户u从当前兴趣点i移动到下一个兴趣点j的转移概率，然后根据转移概率对下一个兴趣点j进行排序，为用户推荐排在前N位的兴趣点。假设用户的签到行为满足一阶马尔科夫性质，那么转移概率可以表示为

xu,i,j=p(Qu,j|Qu,i)，

(1)

式中，Qu,i表示用户u当前所在的兴趣点是i;Qu,j表示用户u下一个访问的兴趣点是j。本文提出的连续兴趣点推荐模型通过融合用户访问兴趣点的个性化偏好和地理距离偏好，更加准确地建模了用户的行为模式。

3.1 个性化偏好

由于张量χ中只有一部分的非零元素，需要利用张量分解技术，将未观察到的转移项进行填充，三阶张量χ的近似可以采用正则分解(canonical decomposition)算法[15]。正则分解算法只考虑用户u，当前兴趣点i和下一个兴趣点j三者中两两之间的交互，用户访问兴趣点的个性化偏好可以被估算为

(2)

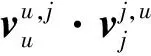
(3)

3.2 地理距离偏好

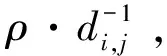
将个性化偏好和地理距离偏好线性相加，得到转移概率的估计值为

(4)

3.3 基于排序学习的优化标准

连续兴趣点推荐是根据转移概率对候选兴趣点进行排序，将排名在前N位的兴趣点推荐给用户。推荐任务关注的是兴趣点对应的转移概率的排名，而非真实的转移概率值，因此可以将推荐任务建模为对兴趣点的排序问题：

(5)

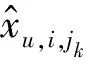
本文采用基于排序学习的优化标准，将历史签到数据中的转移记录组成样本列表，由样本列表组成训练集，通过优化样本列表的排序，拟合用户在兴趣点列表上的偏序关系。具体而言，如果用户u在兴趣点i与兴趣点jm之间的转移频率χu,i,jm，多于用户u在兴趣点i与兴趣点jn之间的转移频率χu,i,jn，那么本文假设用户u在兴趣点i时，对兴趣点jm的偏好程度大于对兴趣点jn的偏好程度，即jm>u,ijn。训练集Dχ可以形式化表示为

Dχ:={listu,i,j|j1>u,i,j2>…>u,ijk,u∈U,i,j∈L}，

(6)

式中，k表示样本列表listu,i,j的长度。

样本列表listu,i,j和训练集Dχ的生成过程如图1所示。图1中转移张量χ中包含所有用户的历史签到数据，转移张量χ中的数字表示用户u从兴趣点i到兴趣点j的转移频率χu,i,j，“？”表示用户在对应的两个兴趣点之间没有观察到的转移记录。转移张量χ中包含了用户、当前兴趣点和下一个兴趣点之间的三元关系，从中可以生成样本列表listu,i,j和训练集Dχ。以列(u1,i1)为例，基于此列生成的训练集是D(u1,i1)={j4>u1,i1j1,j1>u1,i1j2,j1>u1,i1j3,j4>u1,i1j2,j4>u1,i1j3,j4>u1,i1j1>u1,i1j2,j4>u1,i1j1>u1,i1j3}。对于全部转移记录都可以被观察到的列(u1,i4)，生成的训练集是D(u1,i4)={j1>u1,i4j4>u1,i4j3>u1,i4j2}。

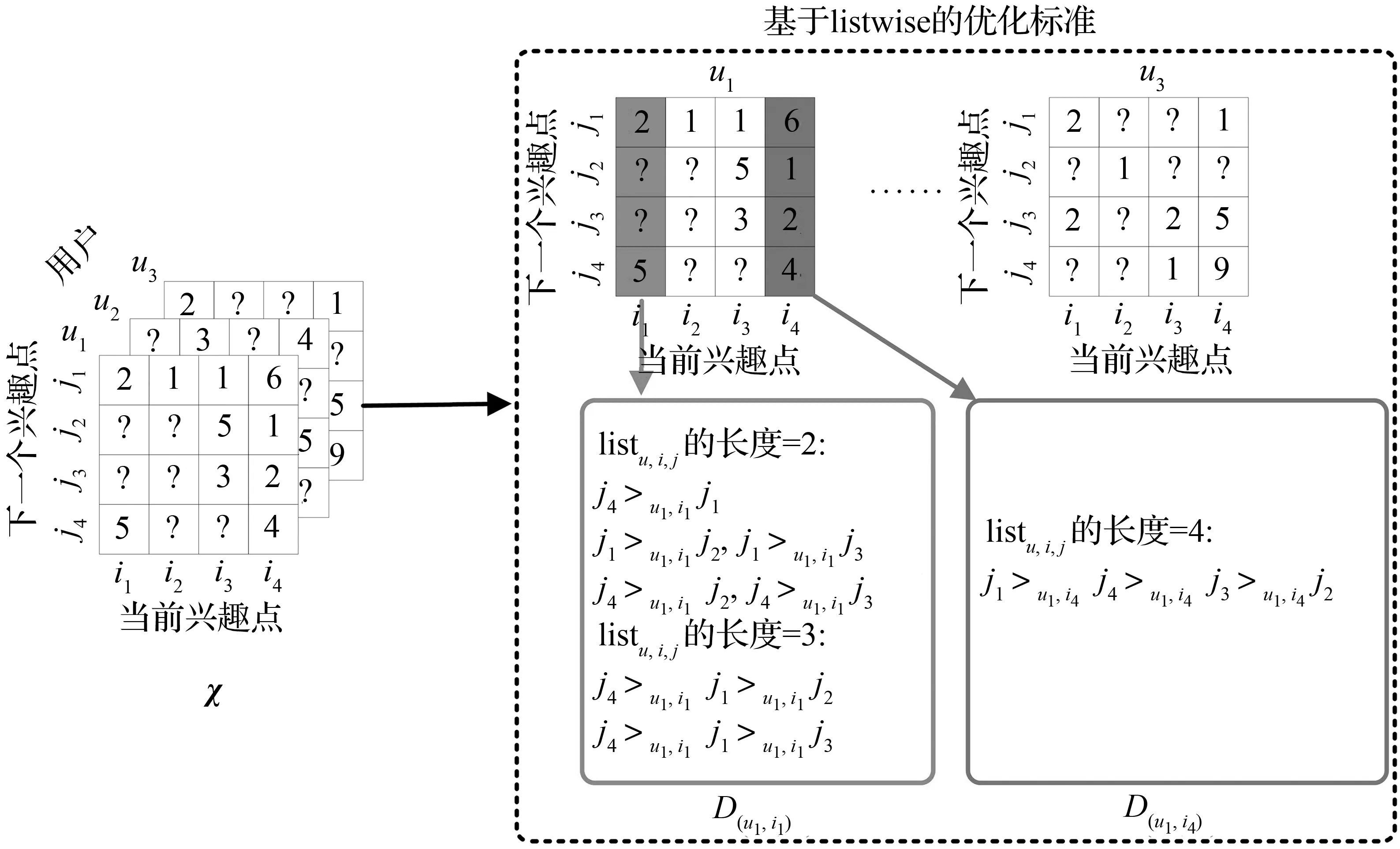
图1 基于排序学习的优化标准示例Fig.1 A illustration of learning to rank optimization criterion

根据贝叶斯法则，基于排序学习的优化标准通过最大化后验概率p(θ|listu,i,j)完成排序任务：

p(θ|listu,i,j)∝p(listu,i,j|θ)p(θ),

(7)

式中,θ表示模型的参数集合。假设每个用户之间是相互独立的，并且训练集Dχ中的每个样本列表listu,i,j之间也是相互独立的，那么模型参数θ的最大后验估计可以表示为

(8)

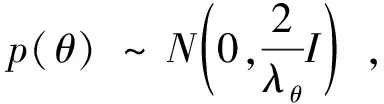
(9)

式中，p(listu,i,j|θ)表示样本列表listu,i,j的似然函数，用于衡量经基于排序学习的优化标准排序后的样本列表与正确排序样本列表之间的相似性。

本文使用文献[13]的模型对p(listu,i,j|θ)进行建模，该模型将样本列表listu,i,j的似然函数定义为正确排序列表与预测排序列表的余弦夹角为

(10)

式中,k表示样本列表listu,i,j的长度;函数σ是严格递增的正函数，本文定义σ为logistics函数,σ(z)=1/(1+e-z)。将式(10)代入式(9)中，得到目标方程如下：

(11)

3.4 参数学习

由于训练集Dχ中样本列表listu,i,j的数量巨大，直接对目标方程(11)进行优化过于费时费力。参考文献[12]，本文从训练集Dχ中随机独立抽取样本列表listu,i,j，使用随机梯度下降算法对目标方程(11)进行优化，同时求解参数θ。参数更新规则如下：

(12)

式中，参数学习率α>0。

排序学习的连续兴趣点推荐模型的步骤如下：

输入：训练集Dχ，列表的最大长度K和参数学习率α

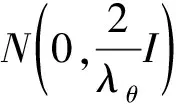
Step 2:当参数θ未收敛，则循环执行以下步骤：

Step 3:从训练集Dχ中随机均匀采样listu,i,j。

Step 4:使用listu,i,j，根据式(12)更新θ;

Step 5:当参数θ收敛，结束循环；

Step 6:返回：参数θ。

输出：用训练集优化求解得到的模型参数θ

4 实验

4.1数据集

本文使用来自Foursquare中洛杉矶和纽约市的两个大规模真实数据集[16]，验证基于排序学习的连续兴趣点推荐模型的性能。本文首先过滤掉这两个数据集中签到次数少于20次的用户，然后把每个数据集分为两个不重叠的集合，将每个用户的签到记录按照签到时间的先后分为两部分，早期80%的签到记录作为训练集，剩下20%的签到记录作为测试集。两个数据集的统计信息见表1。

表1 数据集的统计信息Tab.1 Dataset statistics

4.2 算法性能评价指标

(13)

4.3 对比算法

本文选取以下经典推荐算法作为对比方法：

① 矩阵分解(matrix factorization，MF)[17]。该算法广泛应用于推荐系统中，通过将用户-兴趣点矩阵分解为用户特征矩阵和兴趣点特征矩阵完成推荐任务。

② 概率矩阵分解(probabilistic matrix factorization，PMF)[18]。该算法把用户-兴趣点矩阵分解为用户特征矩阵和兴趣点特征矩阵，并假设用户特征矩阵和兴趣点特征矩阵都服从均值为0的高斯分布。

③ 局部区域内个性化马尔科夫链分解模型(factorizing personalized markov chains-localized regions, FPMC-LR)[4]。该模型用个性化的马尔科夫链模型对用户的签到行为进行建模，并根据签到行为的地理距离约束，将特定距离范围内的兴趣点推荐给用户。

④ 基于潜在行为模式的连续兴趣点推荐模型(global pattern distribution model，GPDM)[9]。该模型使用基于用户-当前兴趣点-下一个兴趣点的三阶张量建模用户的连续签到行为，并融合了地理距离约束，是目前最先进的连续兴趣点推荐算法。

为防止过拟合和模型参数快速收敛到局部最优解，在本文提出模型、GPDM和FPMC-LR中，参数λθ的值均设置为1。模型拟和效果和所需计算资源伴随隐式特征向量维度的增加而增加，为了平衡模型拟和效果和所需计算资源，所有隐式特征向量的维度都设置为16。在实验过程中，用训练集优化求解模型参数的最优值，在测试集中使用这些参数进行推荐。

4.4 实验结果与分析

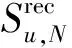
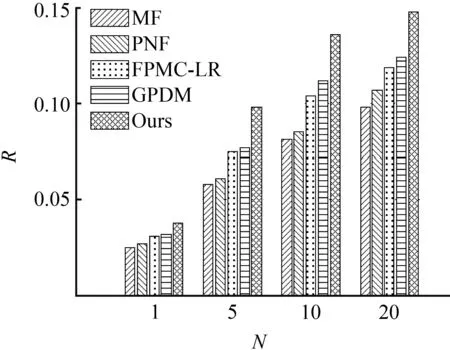
图2 LA数据集上的召回率Fig.2 Recall on LA

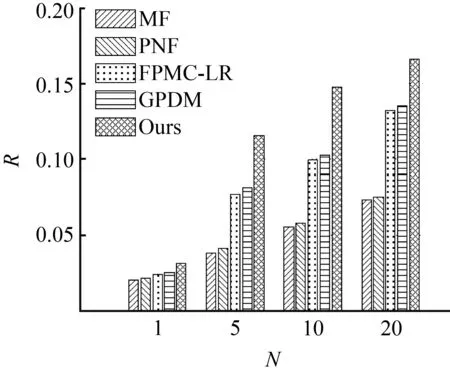
图3 NYC数据集上的召回率Fig.3 Recall on NYC

① 本文模型、GPDM和FPMC-LR都优于MF和PMF，表明经典推荐算法在连续兴趣点推荐任务中效果较差。这是因为MF和PMF只根据签到数据建模用户的兴趣偏好，通过优化用户特征矩阵和兴趣点特征矩阵拟合观察到的转移记录，然后用优化完成的用户特征矩阵和兴趣点特征矩阵进行推荐，忽视了连续签到行为之间的序列关系。本文模型、GPDM和FPMC-LR根据用户当前所在的兴趣点，为用户推荐下一个要访问的兴趣点，充分利用了签到行为的连续性，提高了推荐系统的召回率。另外，本文模型、GPDM和FPMC-LR相比于MF和PMF的性能提升幅度很大，说明在连续兴趣点推荐任务中，地理信息是一项重要的影响因素，用户签到过的兴趣点在地理范围内存在局域性特征。

② 本文模型的推荐性能始终优于GPDM和FPMC-LR，表明基于排序学习的连续兴趣点推荐模型可以有效对用户的行为模式进行建模，从而提高连续兴趣点推荐系统的召回率。GPDM和FPMC-LR均采用对级排序学习算法进行模型优化，本文模型采用列表级排序学习算法进行模型优化，实验结果表明，在连续兴趣点推荐任务中，列表级排序学习算法更加有效地对模型进行了优化，取得了更好的推荐效果。

4.5 样本列表最大长度对召回率的影响

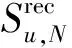
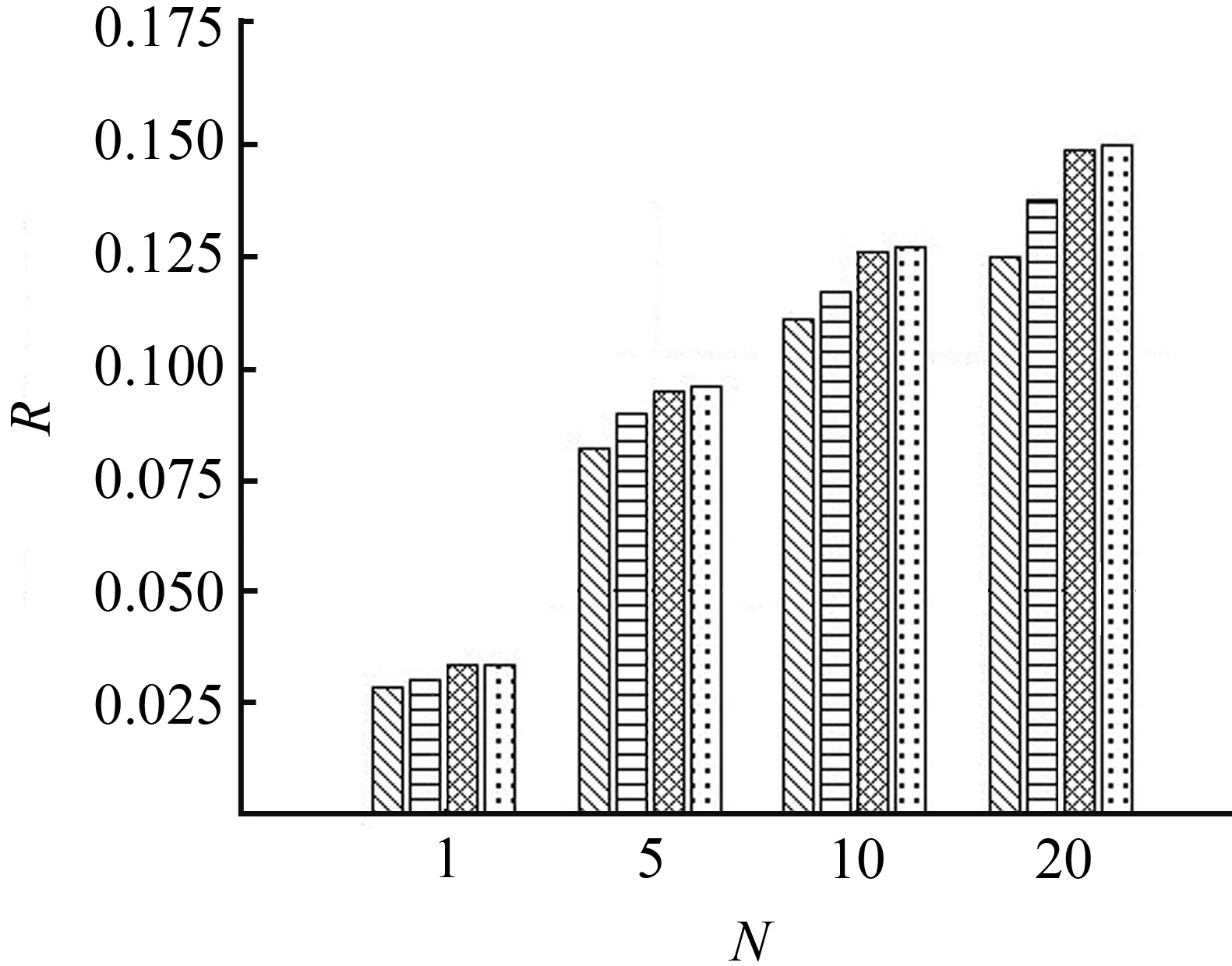
(a) 洛杉矶

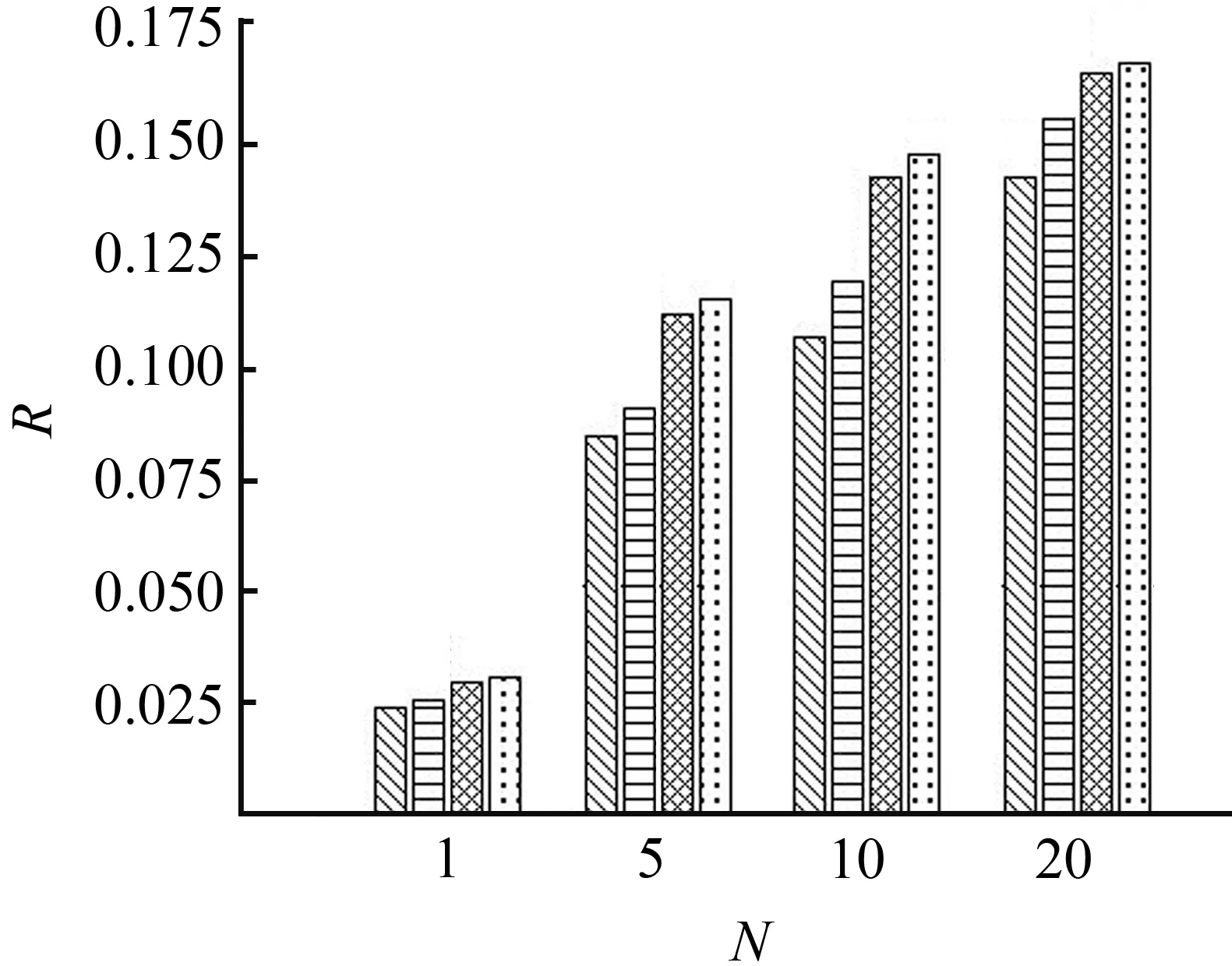
(b) 纽约市

图4 样本列表最大长度对召回率的影响Fig.4 Maximum length impact of list

在基于排序学习的连续兴趣点推荐模型中，将样本列表的最大长度设置为2时，并不等同于传统的Bayesian Personalized Ranking(BPR)算法[12]。从图2至图4可以看出，本文提出的连续兴趣点推荐模型在把样本列表的最大长度设置为2时，推荐召回率仍然高于GPDM和FPMC-LR(GPDM和FPMC-LR均采用传统的BPR算法进行模型优化)。这是因为观察到的转移记录之间、观察到的转移记录与未观察到的转移记录之间都可以组成长度为2的样本列表，这两类样本列表都是基于排序学习的连续兴趣点推荐模型的训练实例；而传统的BPR算法仅使用观察到的转移记录与未观察到的转移记录组成的样本对作为训练实例，从而影响了推荐效果。

4.6 模型的复杂度分析

基于排序学习的连续兴趣点推荐模型的时间复杂度是O(N×K)，其中N是数据集Dχ中样本列表listu,i,j的个数,K是样本列表的最大长度。本文提出的模型具有较低的时间复杂度和良好的可扩展性，可以方便应用于大规模数据集。

5 结语

针对连续兴趣点推荐任务中面临的挑战，本文提出了基于排序学习的连续兴趣点推荐模型，有效提升了推荐性能。具体而言，本文使用三阶张量模型建模用户的连续签到行为，满足了用户的个性化需求；根据用户活动范围的区域性，定义了地理距离偏好，与个性化偏好一起衡量用户对兴趣点的偏好程度，有效缓解了数据稀疏性问题；针对签到行为的隐式反馈属性，将观察到的转移记录和未观察到的转移记录组成样本列表，采用基于排序学习的优化标准求解模型参数。在两个真实数据集上的实验结果表明，本文提出的模型优于当前流行的兴趣点推荐算法。