基于Gabor卷积神经网络的图像分类算法研究

(中南民族大学 生物医学工程学院， 湖北 武汉 430074)

0 引言

基于卷积滤波器的卷积神经网络，由于具有从原始图像像素学习特征的强大能力，在计算机视觉领域被广泛关注和应用。与传统的计算机视觉方法不同，卷积神经网络是多层次的人工神经网络，每个网络层都具有强韧的特征表达能力，对于输入图像的翻转、平移等形式变化具有高度识别性。卷积神经网络中的卷积层、激活层和池化层三个网络结构，能够避免传统神经网络的数据重建，并降低特征提取的困难。

卷积神经网络是一种数据驱动的算法，它从数据中学习稳健的特征，但是通常以昂贵的训练和复杂的模型参数为代价[1]；此外，神经网络的收敛性取决于参数初始化。权值的初始化通常采用均匀分布或正态分布，但这会影响收敛问题，使得网络框架较深的网络在训练时收敛困难。在卷积神经网络中，第一层卷积层主要发挥着浅层特征提取器的作用。 然而，一些深度可视化研究[2-3]，在AlexNet[4]、GoogLeNe[5]等经典卷积神经网络模型中，观察第一层网络的卷积核形状，发现许多自适应滤波器最终收敛于Gabor滤波器，即使所有的滤波器都是随机初始化的；此外，第一层中提取特征的滤波器大多是重复的和有缺陷的。

生物研究[6]表明，Gabor小波具有生物学性质，与哺乳动物大脑视觉皮层的感受细胞的视觉机制十分相似，具有频率特性和方向特性，对图像的边缘信息敏感，能够有效提取边缘特征，感知纹理信息[7]，此外，Gabor滤波器对于光照条件不敏感，在特征提取过程中不会受光照亮度影响。Gabor滤波器被广泛应用于传统的计算机视觉方法中，目前，在深度学习领域已有部分研究[8-9]。本文基于Gabor滤波器的优越生理特性和数学计算特性，针对卷积神经网络强大的学习能力及其存在的可改进之处，将两者融合，发挥各自优势。

理论上将Gabor滤波器作为卷积核来提取有效特征的能力会高于普通卷积核。根据Gabor滤波器的函数表达式可知，在反向传播的参数更新过程中，其只需学习更新λ，θ，ψ，γ四个参数(σ与λ关联)，可以有效地降低网络的训练复杂度，从而在保持较高的特征表现能力的同时，形成更加紧凑的深度学习模型[10]。此外，根据Gabor滤波器的特性，在使用Gabor函数时，需要给定五个参数λ，θ，ψ，σ，γ的初始化范围和学习范围，避免随机初始化，提高网络的收敛速度。

基于Gabor滤波器的生物特性、提取特征的能力，以及在反向传播时参数更新量的优势，笔者提出一种改进卷积神经网络的方法，自定义Gabor卷积核与卷积神经网络相结合，形成Gabor卷积神经网络(gabor convolutional neural networks, GaborConv),网络中的Gabor卷积层从频域的不同尺度和方向上提取多层次特征，为网络的学习增加有效特征，提高学习能力。Gabor卷积神经网络适用于图像识别、图像分类、图像分割等计算机视觉任务。本文研究表明，Gabor卷积层在特征提取方面表现良好，处理复杂数据的能力优于卷积神经网络，且在网络中能有效减少训练参数数量，释放计算机内存占用。

1 二维Gabor卷积神经网络模型

1.1 二维Gabor滤波器

Gabor滤波器是一种小波，其在数学领域的应用始于1946年，由英国的物理学家Gabor首先提出一维Gabor函数[11]。到1980年，DAUGMAN[12]将一维的形式扩展到二维，形成二维Gabor函数。Gabor滤波器具有良好的时域和频域变换特性，可利用Gabor函数构造由不同参数引起的不同尺度方向的滤波器。Gabor滤波器的生理特性是经过科学家的严谨证明得到的，文献[13]的研究表明一维 Gabor函数可以很好地描述简单细胞的感受野。DAUGMAN对视觉皮层感受野的分布进行了二维光谱分析，并证实了这种关系。所有简单的单元都可以用一组二维Gabor小波建模，在频域以对数方式采样。

本文采用的是二维Gabor滤波器，输入数据是二维图像。二维带通Gabor滤波器是由特定频率和方向的复正弦波调制的椭圆高斯包络线，其中谐波分量使滤波器对空间频率敏感，而高斯分量限制了对输入图像局部区域的频率敏感程度。Gabor函数的复数表达形式如下：

(1)

实数部分表达形式为

(2)

虚数部分表达形式为

(3)

其中：

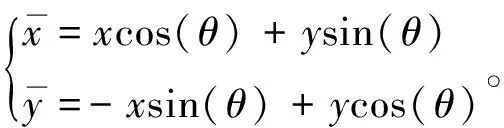
(4)

Gabor函数的各个参数对滤波器的形态均有不同的影响，其中，θ表示滤波器的方向，本文选择的取值范围是0～π；λ表示滤波器的波长，其值以像素为单位；ψ表示Gabor函数的中正弦或余弦因子参数的相位偏移，本文的取值范围是0～π；γ表示空间纵横比，人眼的最佳接收范围[14]是(0.3～0.7)；σ是Gabor函数的高斯因子标准差，其值由带宽b决定。

(5)

标准差σ和波长λ相互关联，两者的关系式如式(6)所示。

(6)

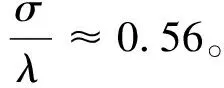
(7)

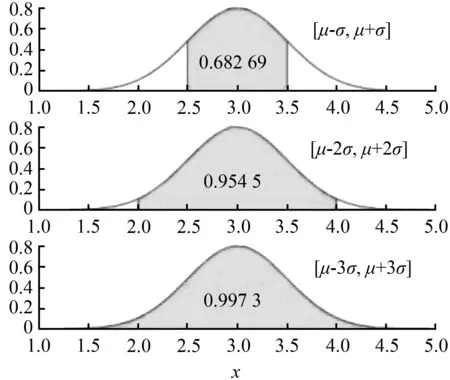
图1 高斯函数曲线图像Fig.1 Gaussian function curve image

Gabor函数是复正弦波调制的椭圆高斯包络线，其中高斯函数图像的区间取值范围与滤波器核尺寸的大小相互关联。由式(7)可知，窗口尺寸大小的选择取决于参数σ，在高斯函数图像中，函数曲线在(μ-3σ,μ+3σ)的区间范围内时，所占面积约为总面积的99.7%，因此，当半径为3σ，即窗口大小为6σ×6σ时，窗口尺寸几乎能包含99%以上的有效范围。图1所示为高斯函数曲线在(μ-σ,μ+σ)，(μ-2σ,μ+2σ)，(μ-3σ,μ+3σ)三种取值区间的覆盖范围。

1.2 网络结构

在设计一个深度神经网络时，除了网络的学习性能之外，网络训练参数数量也是不可忽视的问题。在神经网络中，感受野需要覆盖整个相关图像区域，因为在图像预测时，需要一个足够大的感受野来捕获每个像素周围的局部上下文信息。现存的一些改进感受野的研究，尝试着扩展感受野，将大尺寸的卷积核在浅层卷积层使用，或使用小尺寸卷积核堆叠几层。然而，增大感受野的大小，会导致可训练参数的数量和计算成本的快速增长。

在一个标准的卷积层中，设有K个尺寸为m×m的卷积核，以及c个输入特征，那么该卷积层的可训练参数数量为(m×m×c+1)×K，相比之下，对于本文所提出的Gabor卷积层而言，每个Gabor卷积核只需更新4个参数(σ与λ关联)，无论卷积核尺寸多大，相同条件下，Gabor卷积层的可训练参数数量为(4×c+1)×K。因此，将Gabor卷积核作为特征提取器，有利于设计更紧凑的网络。Gabor卷积神经网络前向传播和反向传播过程如图2和图3所示。

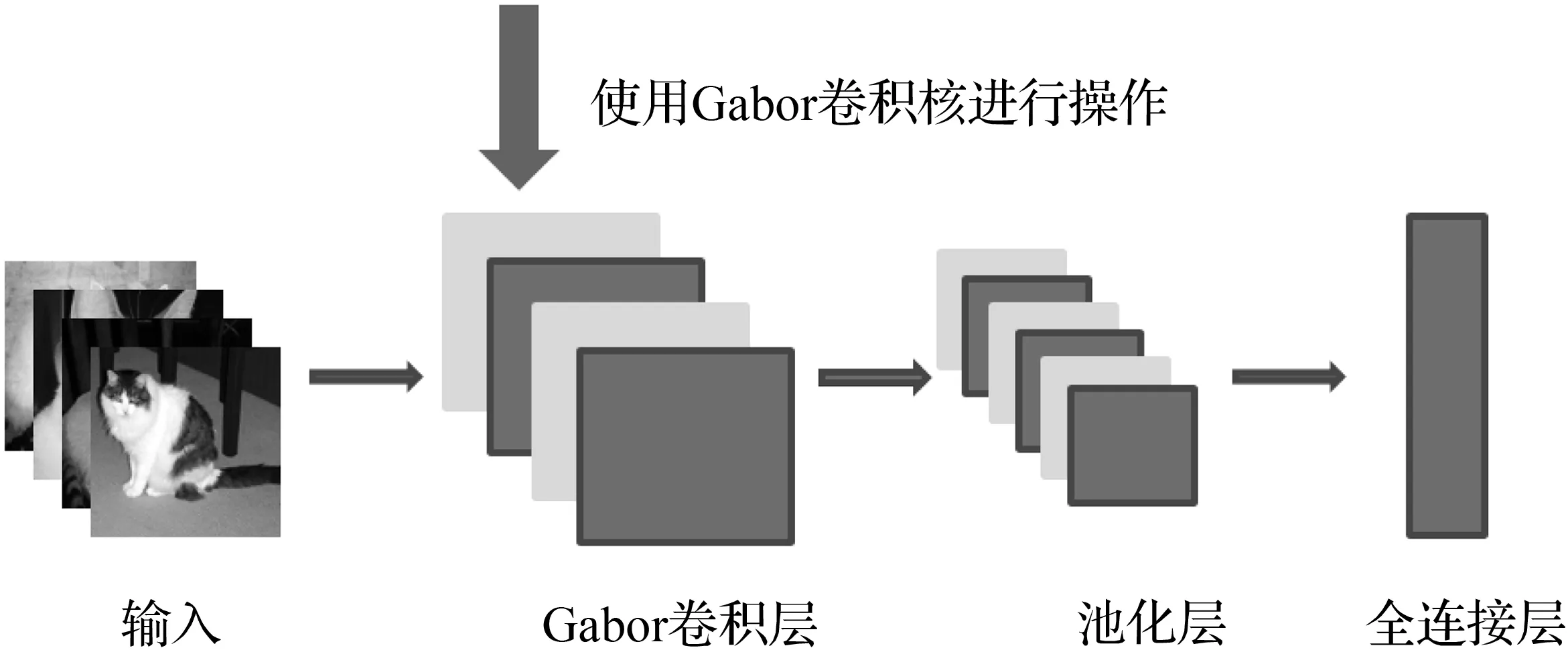
图2 Gabor卷积神经网络前向传播Fig.2 Forward propagation of Gabor convolutional neural network

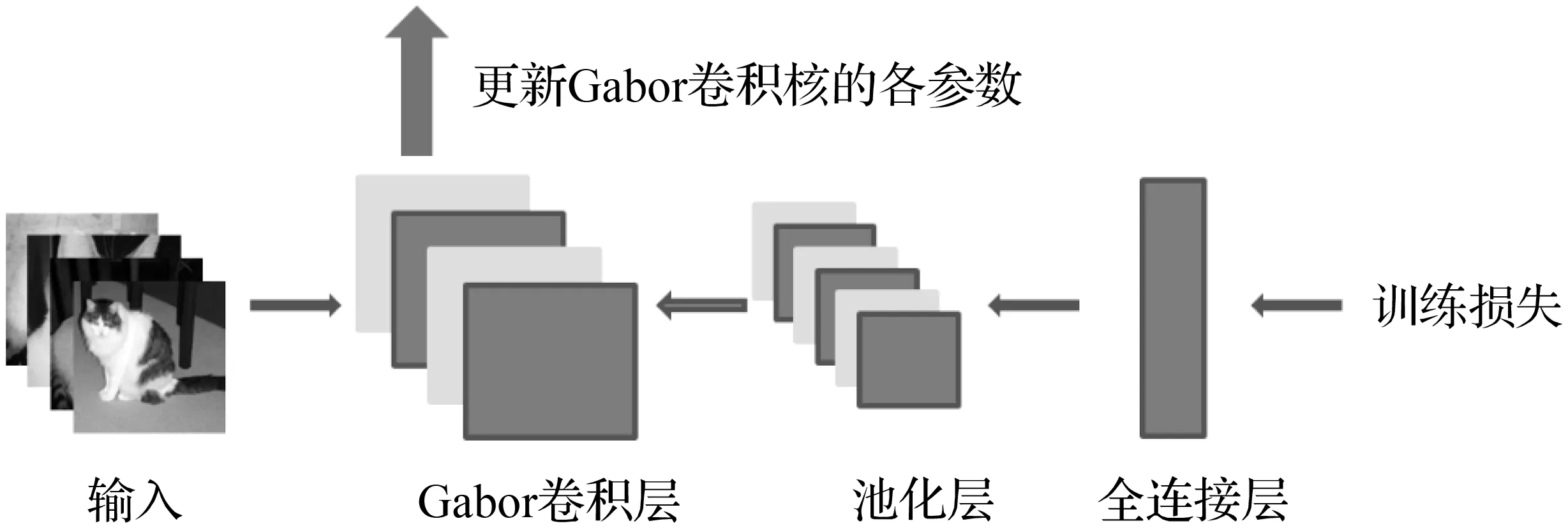
图3 Gabor卷积神经网络反向传播Fig.3 Back propagation of Gabor convolutional neural network

VGGNet是卷积神经网络的经典模型[15]，是由Karen Simonyan和Andrew Zisserman在ILSVRC2014竞赛中提出的一种网络模型，VGGNet的创新之处在于将小尺寸的卷积核堆叠代替大尺寸卷积核，2个3×3的卷积核可以代替5×5的卷积核，并且不影响网络效果，这样在很大程度上减轻了计算量。VGG16是随后被广泛使用的一种模型，其由13层卷积层和3层全连接层组成，每个卷积层后面都紧接着ReLU激活函数和BatchNorm层，网络输入为224×224的三通道彩色图像。

本文关于Gabor卷积核的网络主要基于VGG16的网络模型，其结构如图4所示。图4(a)为VGG16网络的具体结构；图4(b)、图4(c)为基于VGG16搭建的GaborConv13网络结构。GaborConv13网络是将VGG16网络的第一层普通卷积核替换为Gabor卷积核，使第一个卷积层变为Gabor卷积层。图4(b)所示网络结构用于CIFAR10数据集，该数据集图像尺寸仅为32×32，因此Gabor卷积核的尺寸设为5×5。图4(c)所示网络结构用于猫狗和Mini-imagenet数据集, 图像尺寸为224×224，Gabor卷积核的尺寸设为9×9，并将第一个Maxpool设为4×4，加快特征图尺寸缩减。三个网络结构中，每个卷积层后面都会加BatchNorm层和ReLU激活函数。本文将GaboConv13和VGG16两个网络模型作为实验对比模型，在上述3个自然图像分类数据集上开展实验，并根据网络训练过程中的训练损失图、网络分类精确度以及网络训练参数数量3个指标来评价网络的整体效果。

(a) VGG16

(b) 第一层为5×5Gabor卷积核的GaborConv13

(c) 第一层为9×9Gabor卷积核且第一个池化层为4×4的GaborConv13

1.3 二维Gabor卷积的反向传播过程

在Gabor卷积核中，需要对每个Gabor滤波器的参数进行优化。梯度下降算法通过反向传播[16]的方式，根据目标函数调整优化滤波器的参数，而Gabor卷积核同样通过反向传播的学习方法来获取反映视觉属性的Gabor滤波器参数，本节将对Gabor函数的反向传播做简要的推导。设L为损失，α为学习率，p为需要更新的参数，其中p∈{λ,θ,ψ,σ,γ}，参数更新遵循误差反向传播算法:

(8)

(9)

则Gabor函数中的5个参数更新的公式如下：

(10)

(11)

(12)

(13)

(14)

根据以上的公式，Gabor函数的各个参数在网络训练过程中不断迭代更新。梯度下降算法根据上述对参数求偏导的方式进行扩展，以此将所有错误损失归因于Gabor函数的参数，而不是归结于滤波器结构，因此，可以通过更新滤波器参数来调整滤波器，从而避免盲目调整滤波器结构而忽略网络结构。

2 实验结果与分析

本文实验环境为Centos系统，配置了Intel(R) Xeon(R) Gold 5118 CPU @2.30 GH和NVIDIA Tesla V100-SXM2显卡的大型浪潮服务器，软件环境为anaconda4.5.4，Python3.6.9，Pytorch1.1.0。网络模型的初始学习率均为0.001，每迭代20次减小10倍，优化器选择SGD。

根据上述提出的对比实验方案,开展了相应的实验验证Gabor卷积神经网络的可行性，检验其在计算机视觉任务中的表现。本文开展实验对自然图像数据集进行分类，选用Cat&Dog数据集、CIFAR10数据集和Mini-imagenet分类数据集。其中，Cat&Dog数据集是Kaggle竞赛的比赛数据集；Mini-imagenet数据集节选自ImageNet数据集，DeepMind团队首次将其用于小样本学习研究，Cat&Dog和Mini-imagenet的图像尺寸均处理为224×224；CIFAR10是由Hinton的学生Alex Krizhevsky和Ilya Sutskever整理的一个用于识别普适物体的小型数据集，其图像尺寸为32×32。本文使用VGG16网络模型和GaborConv13网络模型对三个数据集进行分类任务。图5所示为两个网络模型在每个数据集上的训练损失对比图，从训练损失曲线可以看出，GaborConv13的收敛速度比VGG16有所提升。

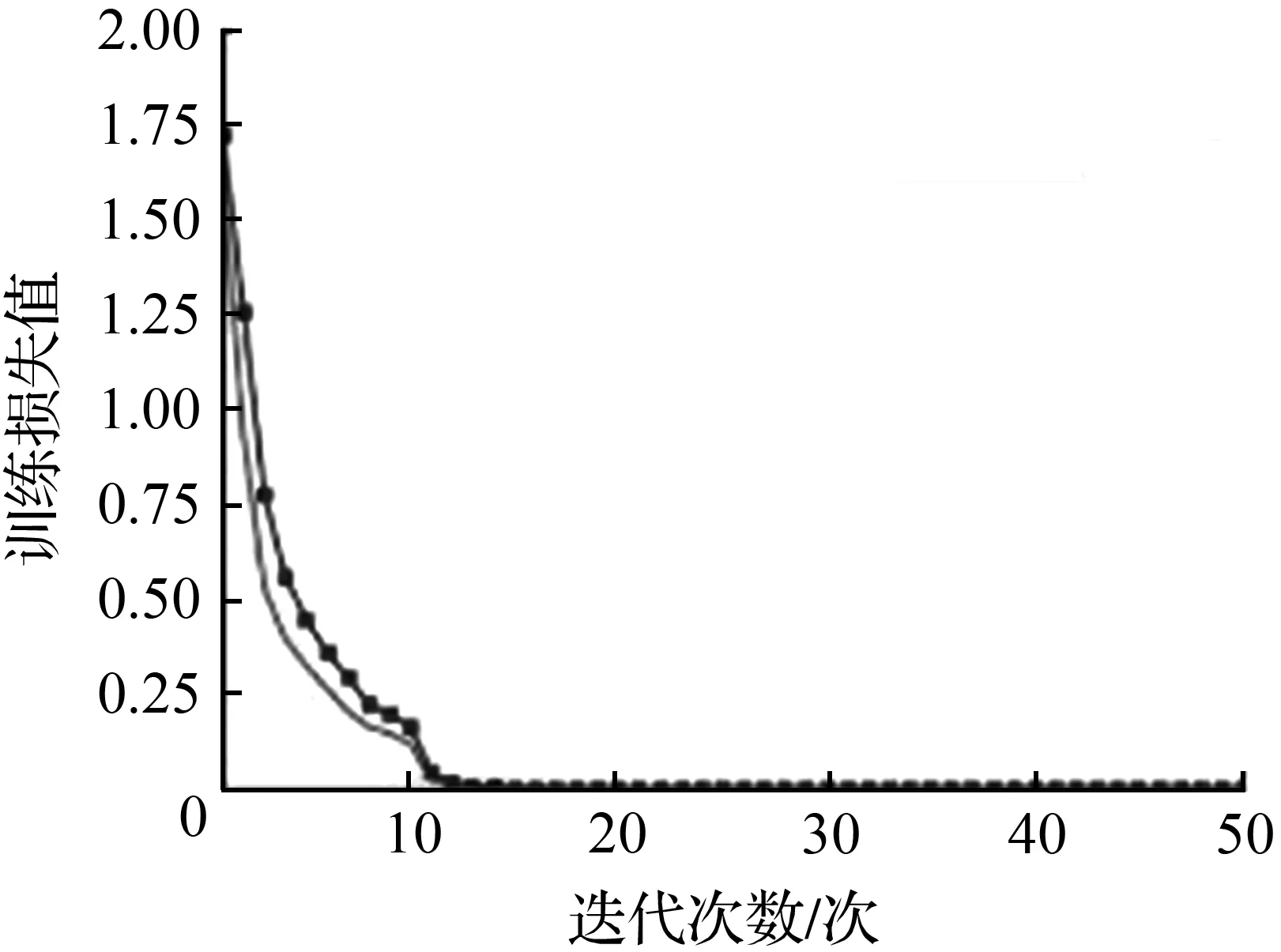
(a) Cat & Dog数据集

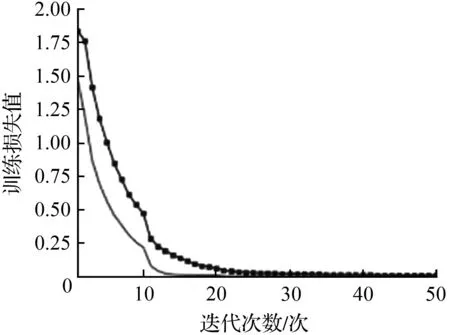
(b) CIFAR10数据集

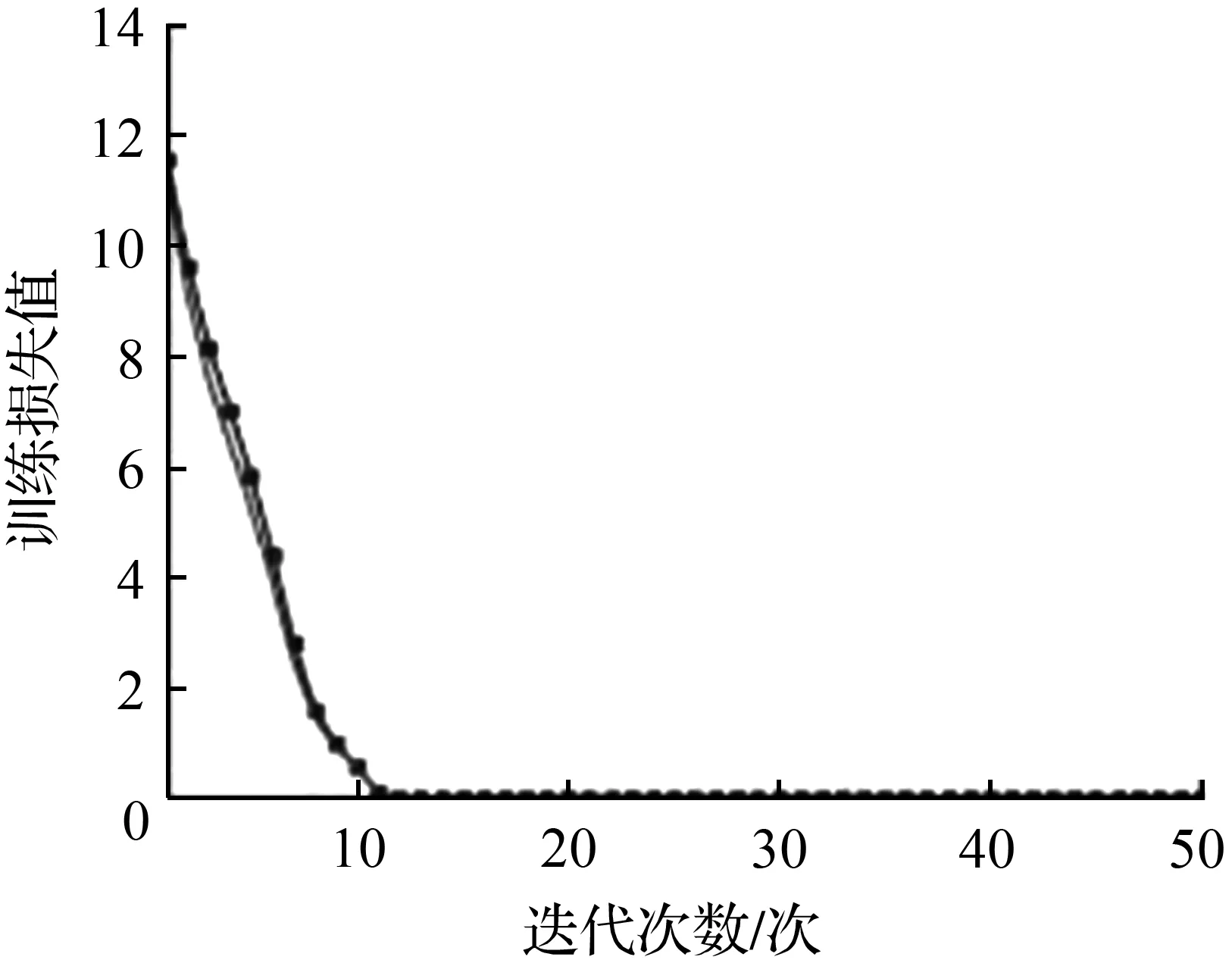
(c) Mini-imagenet分类数据集

表1对比了VGG16和GaborConv13两个网络模型在三个图像分类数据集上的测试分类精确度。从表1中可知，GaborConv13在缩减网络层数的情况下，在三个数据集上的测试分类精确度均优于VGG16。由实验结果可知，Gabor卷积核的方向性核频率特性在特征提取中发挥优势，使得GaborConv13网络性能优于VGG16。GaborConv13网络的性能与Gabor卷积核的参数设置有很大关联，因此，对Gabor函数的各参数深入研究很有必要。

表1 两个网络模型在三个数据集上的分类精确度Tab.1 Accuracy of two network models on three data sets %

表2分别比较了两个网络模型的第一层参数量和网络总体参数量，由于GaborConv13的第一层使用Gabor卷积核，有效压缩了网络模型的深度，与VGG16相比，GaborConv13模型不仅第一层参数量减少，而且网络总参数量也大幅度降低，减轻了网络的计算量。

表2 两个网络模型的参数量对比Tab.2 Comparison of the number of parameters of the two network models

为了对比GaborConv13模型与其他研究方法的网络性能，采用CIFAR10数据库进行实验比较，具体的对比结果见表3。文献[17]主要通过在卷积层中加入正则化方法来减少计算开销，然而提出的方法并不能减少参数量；文献[18]提出了一种新型卷积模块，该方法在保证分类精确度的同时，能够在低容量硬件上部署较大的网络，减少计算量，不过与GaborConv13相比，其卷积层的参数量并没有降低；文献[19]采用的半监督学习，引入自集成方式，有效提高分类精度，与其相比，本文在CIFAR10上的分类精确度略低，但本文的研究目的与其不同，本文主要研究Gabor卷积核的特征提取能力及网络模型参数量。总体而言，本文的研究内容具有较好的研究意义，所提出研究方法具有一定优势。

表3 不同研究方法在CIFAR10上的分类精确度Tab.3 Classification accuracy of different research methods on CIFAR10

3 结论

实验研究和实验结果表明，本文设计的Gabor卷积核，其特征提取能力优于普通卷积核，Gabor卷积核的使用能够降低神经网络的深度，并且能达到与卷积神经网络的一样学习效果，同时减少网络参数数量，一定程度上解决深层的卷积神经网络的学习对计算机内存的占用问题。总体而言，实验效果达到预期期望，在之后的学习中，会尝试将二维Gabor卷积神经网络运用在其他的计算机视觉的任务当中，检验网络的鲁棒性。今后的学习研究中，考虑将Gabor滤波器与卷积神经网络的研究往两个方向开展，其一，在二维层面，考虑是否研究Gaussian卷积核，并将Gabor卷积核与之随机混合使用；其二，将二维Gabor滤波器扩展到三维层面，自定义三维Gabor卷积核，用于三维的计算机视觉任务。这是根据目前的研究成果所设想出的两种研究思路，在后期的科研任务中，会继续深入研究。