机场航空器污染物排放测算的不确定性分析

朱昶歆 胡 荣 张军峰 刘博文

(南京航空航天大学民航学院 南京 211106)

0 引 言

有研究表明，2017年，民航NOx排放占欧盟运输NOx排放总量的14%，占欧盟排放总量的7%，预计未来航空业排放的影响愈发显著[1].我国民航运输业多年来一直保持高速发展，2016年民航污染排放占全国排放总量的3%，未来可能会持续上涨[2].

在实施民航污染物减排行动之前，需要对民航污染物排放进行准确测算，建立可靠的排放清单.国内外相关机构及学者提出了多种用于定量测算航空器污染物的方法.随着模型愈趋复杂，不论是模型假设条件还是模型参数带来的不确定性都会给最终的计算结果带来较大的偏差.因此，对于决策制定者来说，需要明确模型存在的不确定性因素，并且通过后续的模型优化使输出偏差的变化尽可能平稳；需要挖掘在不同决策应用场景下测算结果的变化机理，以此根据模型的不确定性来评价测算结果[3].虽然，航空器污染物排放测算的不确定性分析并不会降低排放测算本身固有的不确定性，但可以捕捉不同结果发生的相对可能性、挖掘模型中存在的关键不确定性因素、确定未来改进排放测算准确性的优先努力方向、指导有关测算方法的选择，并完善航空器排放清单的基本组成内容.决策者可基于不确定性的量化结果制定更加具有针对性的决策，以此提升未来决策实践环节中的有效性[4].

根据运行状态，航空器污染物排放可大致分为两个阶段：CCD(climb cruise and descent)阶段与LTO(landing and takeoff)阶段.考虑到LTO阶段污染物排放足以造成机场和附近居民区的空气污染并且极易对周边居民健康产生更直接的影响；同时，航空器在LTO阶段发动机工作状态、飞行环境条件等变化频繁，这一航空器运行复杂性对污染物排放测算带来更多的不确定性影响[5].因此，本文针对LTO阶段的航空器污染物排放，提出污染物排放测算过程中不确定性的分析框架，梳理不确定性因素及其来源，总结不确定性表征与分析方法，并以广州白云国际机场为例进行验证，以期为提高航空器污染物排放测算的准确性与可靠性、科学评估民航减排成效提供参考.

1 不确定性来源

1.1 模型不确定性

模型不确定性来源于机场航空器污染物排放测算模型和关于排放情景的不适当假设.对于决策者来说，不仅关注模型的测算结果，也关注导致测算结果差异的建模假设[6].与模型相关的不确定性通常难以量化，可从假设条件、模块评估和系统评估三方面加以论述.

1.1.1假设分析的不确定性

通过模型假设条件分析可明确测算关键不确定性因素来源.例如，美国联邦航空局开发的SAGE(system for assessing aviation’s global emissions)模型中主要假设包括：标准日环境温度、未修正的高空风、不确定的空气动力学指标和发动机指标、航空器起飞重量和飞行速度的简化、航班计划数据库的使用、排放指数的不确定性等.现有航空器污染物排放测算模型的关键假设见表1.

表1 排放模型关键假设

1.1.2模块评估的不确定性

模块评估涉及对各个子模型的评估，目的是讨论其涵盖方法、模型的不确定性.文献[3]将模块评估划分为飞行性能、燃油评估,以及排放评估三部分.其中，在飞行性能模块推力计算过程中风和航空器性能参数为关键不确定性来源；燃油评估模块不确定性涉及升力系数曲线取值、ICAO的EEDB(aircraft engine emission databank)数据库参数选用及插值计算[7]；排放评估模块是通过排放模型计算NOx、HC、CO、SOx几类气体污染物排放量，常见的方法包括ICAO、EPA和EMEP等推荐方法[8].

1.1.3系统评估的不确定性

系统评估是检验模块评估不确定性对机队级别排放的影响.主要涉及机队级别数量的选取、机型的涵盖，确保分析样本足够丰富从而使分析结果具有普遍参考意义.例如使用SAGE模型预测的误差相较于单个航班在相同置信水平下有所减小.

模型的不确定性通常不具有明显特征或者根本不具有特征.虽然在现实分析中，模型和参数形式的不确定性会同时出现，但在后续的量化分析过程中只涉及参数不确定性.

1.2 参数不确定性

参数不确定性来源于排放测算模型中每个参数值的使用，其分析目的是鉴别出模型中影响最大的不确定性因素，并量化它们对系统级性能影响的程度.

针对LTO阶段航空器污染物排放测算，参数不确定性主要涉及如下关键参数.

1)LTO边界高度 LTO循环定义为大气混合顶部高度3 000 ft(914 m)高度以下的所有飞机活动.其边界高度由监管标准决定，并且代表大气混合高度的近似值[9].研究发现大气边界高度会随天气的不同而变化，且污染物排放会随边界高度变化而变化[10].

2)污染物排放指数 由于数据不公开、需要昂贵的实测活动或者无法开展实测(如无法测量起飞过程中发动机的实际排放指数)，这就使得实际污染物排放指数与理论排放指数存在差异，给最终的测算结果带来不确定性.

3)阶段运行时间 航空器在不同阶段的运行时间关系到排放总量的计算.根据国外机场已有数据统计估算得出阶段运行时间不确定性为约10%[11].使用Watterson等[12]所述方法估算阶段运行时间的不确定性约为20%,该结果与Patterson等[13]观察到的阶段运行时间的变化模式类似：起飞和爬升的偏差为10%～20%，进近为15%～20%.

除上述因素之外，发动机性能退化、ICAO排放数据库偏差、运行的气象条件等也会带来LTO阶段测算时的不确定性[14].

1.3 观测不确定性

观测值可能由于周围环境、测量仪器和测量方法的误差导致出现不确定性.例如：在机场附近设置污染物监测点，则监测点的污染物监测明显受到机场的车辆活动、周边高速公路，以及高架桥的影响[15].

2 不确定性表征方法

2.1 概率分布

当大量的实验数据可用于估计分布时，概率分布可描述一个参数的取值范围以及不同值的相对可能性.当有充足的信息能够确定统计变量的基本概率分布，应该以95%的置信区间作为不确定性估算范围.

实际情况中，往往采用统计推断的方法匹配合适的概型[16].《IPCC国家温室气体清单优良作法指南和不确定性管理》提供了相关建议：将标准统计拟合检测、变化系数判断和专家判断相结合来确定概率分布.Simone[17]提出在大多数情况下，概率分布可假设为正态分布、三角分布.

2.2 统计指标

机场航空器污染物排放测算的不确定性分析中通常还可以用统计指标来表征参数的不确定性范围，一般包含平均值、标准差和百分位数.

统计指标中的平均值和标准差可以较为精确地度量数据的离散程度，通过比较模型的输出与官方报告数据之间的差异，以此推断出模型测算不确定性的区间范围.百分位数可以揭示小于这个样本值的样本数量在整个样本集合中所占的百分比.以2008年在英国机场LTO阶段测算的CO2排放为例，其总量中位数为2.02×109kg，使用第5和第95个百分位数表示其不确定性范围为中位数的[-14%,14%].

2.3 模糊数学理论

模糊数学理论通过隶属度函数来量化对象的类别归属程度，使用一个属于[0,1]区间的实数值来表示隶属度，隶属度越高变量所属范围越大，反之变量所属范围越小.该方法的关键问题是寻找合适的隶属度函数，在实际应用中可与概率方法相互补充.

2.4 非概率区间法

非概率区间法不同于概率方法和模糊数学方法，仅需获取参数的上界和下界而不用考虑其具体分布，由于此类方法不涉及参数的概率分布函数，也被称为非概率不确定分析法，在小样本问题中是概率方法的有力补充，在节省大量成本的同时给出较为准确的输出范围估计.

基于上述表征方法，进而可以针对排放模型科学地量化不确定性.例如：通过泰勒级数展开进行变量不确定性传播分析；采用蒙特卡洛模拟确定输入参数不确定性对于总误差的贡献；使用统计分析以检验模型测算值与输入数据之间的关联程度；运用敏感性分析识别模型的关键不确定性因素，等等.

3 实例分析

针对参数不确定性中的运行时间、燃油流量以及大气状况，以广州白云国际机场为例，选取11个机型累计185条航班QAR(quick access recorder)数据进行LTO阶段污染物测算的单一参数以及参数组合的不确定性量化分析.

3.1 LTO阶段排放模型

根据ICAO提供LTO阶段污染物排放模型，并结合气象因素对各污染物排放指数修正结果，可计算飞机污染物排放量：

(1)

式中：Ej为污染物j的排放量；n为发动机数量；t为各阶段运行时间；IjM为污染物j的修正排放指数；f为燃油流量.

由于ICAO提供的标准污染物排放指数与实际推力下的排放指数存在较大差异，采用线性插值法可对飞机不同状态下的排放指数进行拟合计算：

(2)

式中：I为实际推力下的污染物排放指数；ITO为起飞阶段排放指数；IC为爬升阶段排放指数；IA为进近阶段排放指数；II为慢车滑行阶段排放指数；fTO为起飞阶段燃油流量，fC为爬升阶段燃油流量；fA为进近阶段燃流量；fI为慢车滑行阶段燃油流量.

考虑大气环境与飞行参数影响，污染物排放指数与环境的气压、温度与大气湿度等相关，故插值计算的排放指数结果还需进行气压、温度与大气湿度的修正换算.

(3)

(4)

式中：IjM为污染物j的修正排放指数；j为污染物种类；Ij为污染物j实际推力下的排放指数；φ为大气相对湿度.

3.2 运行时间分析

ICAO建议在LTO循环内的污染物排放可划分为四个阶段：高度为0 m的滑行阶段、高度为0～304 m的起飞阶段、高度为>304～915 m的爬升阶段以及高度为>915～1 000 m的进近阶段.根据上述高度划分标准，对数据集进行处理并统计，最终运行时间对比结果见图1，其中误差棒代表2σ置信度.

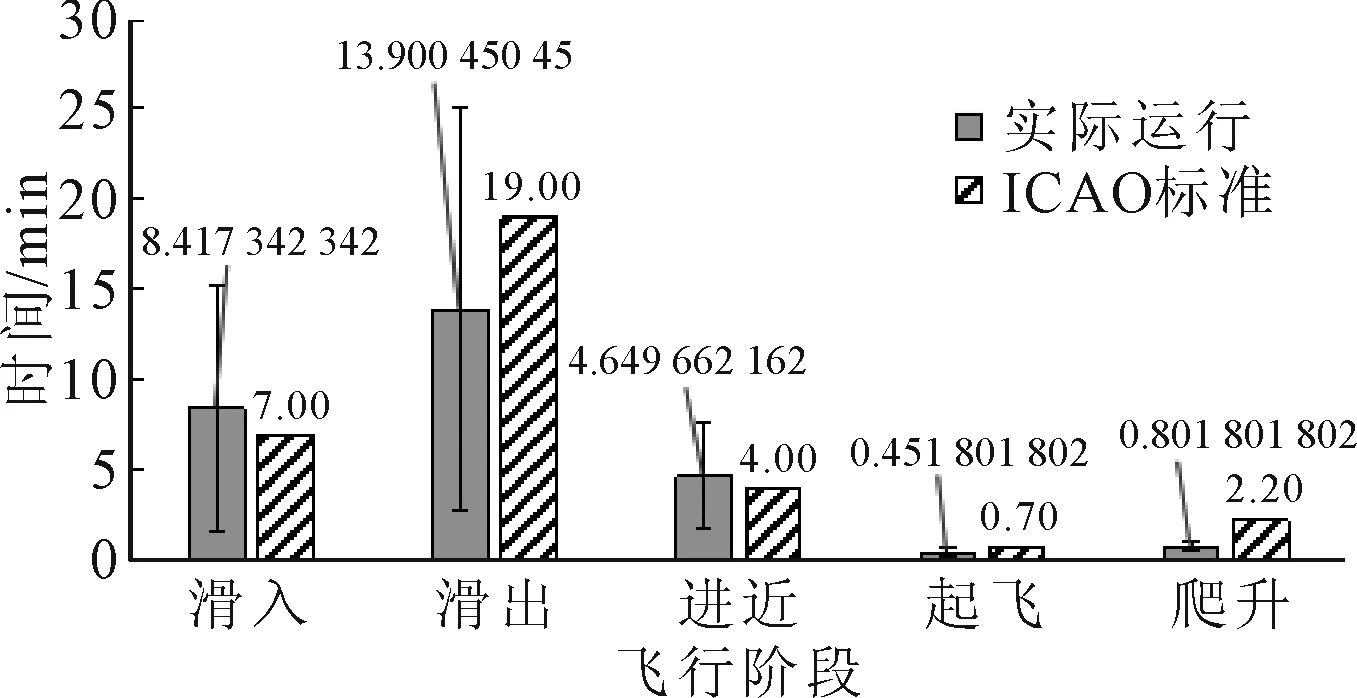
图1 各阶段运行时间对比

统计结果表明:由于场面航班量及机场特性等因素导致在滑入和滑出阶段的平均运行时间波动范围较大.滑入时间和滑出时间平均值相较于标准值分别相差-1.42，5.1 min，实际总滑行时间小于标准值约4 min.进近和起飞阶段运行时间平均值较接近标准值，而爬升阶段平均值与标准值相差75%，造成差异较大的原因可能是忽视实际大气混合高度与LTO边界高度标准值之间的偏差以及ICAO标准值设定过于保守.

3.3 燃油流量分析

测算模型中涉及的排放指数通常与燃油流量密切相关，统计各飞行阶段发动机燃油流量记录平均值，并与该机型发动机对应燃油流量标准值进行对比分析.以A320机型为例，该机型使用的发动机型号为CMF56-5-A1，其参数通过EEDB获取，对比结果见图2.

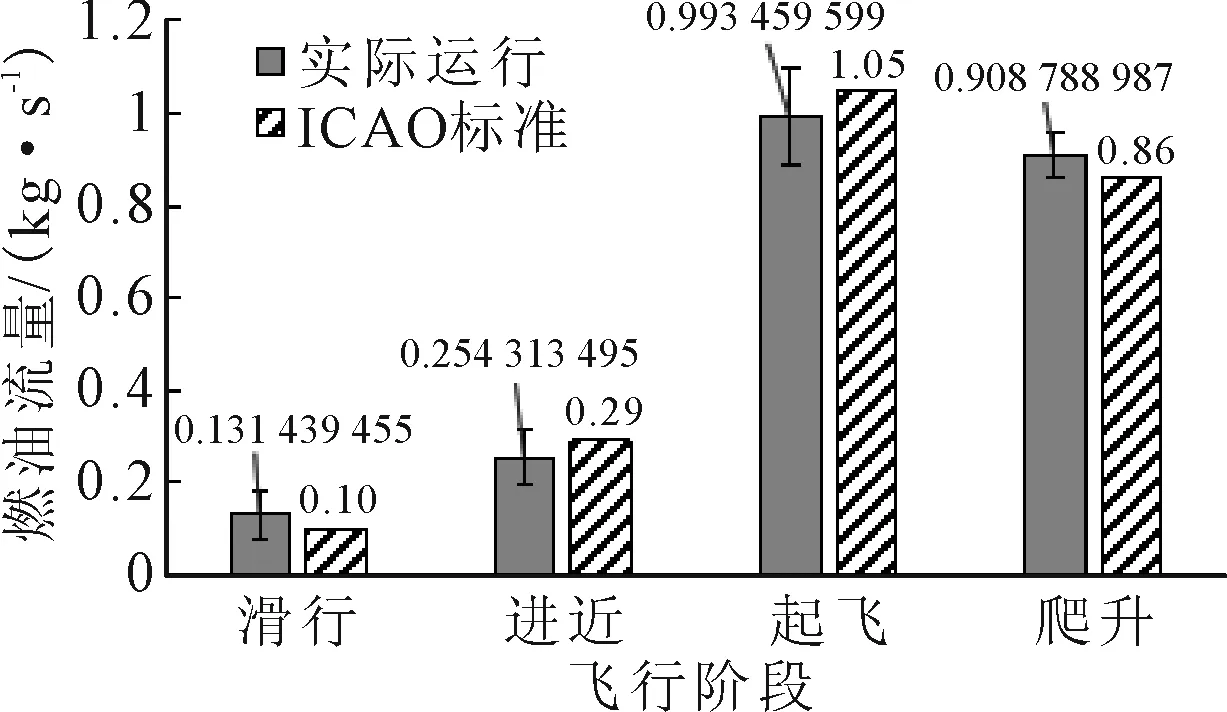
图2 燃油流量对比

图2表明在起飞和进近阶段的实际燃油流量平均值均接近标准值，而滑行和爬升阶段实测值略高于标准值.考虑到广州白云机场航班起降架次较多，飞机在滑行阶段可能会多次时停时走从而导致加速次数的增多；爬升阶段存在由于离场程序限制而转向、平飞的情况，都会使燃油流量出现波动从而带来不确定性.

3.4 排放分析

选择燃油流量、运行时间、温度、压强作为研究变量，基于排放模型(1)～(4)运用蒙特卡洛模拟量化单个发动机排放测算结果的不确定性.设定模拟轮次为30 000，图3为最终得到HC、CO、NOx三类污染物不同飞行阶段的排放测算结果.

图3 各污染物不同阶段排放量

观察到滑行阶段三类污染物排放量测算结果不确定性范围较大，并且HC，CO排放量分别低于标准值15%和17%，而NOx反而高于标准值，可能是由于滑行阶段时间的不确定性造成.进近阶段HC排放量远低于标准值，而CO排放量高于标准值，NOx较接近标准值但不确定性较高.起飞和爬升阶段三类污染物排放量均低于标准值，其中爬升阶段NOx与标准值相差约57%.

3.5 敏感性分析

为能够清晰地识别关键不确定性因素，使用Sobol法对排放模型进行敏感性分析，选取燃油流量、运行时间、温度、压强作为分析参数，计算得到各变量的一阶以及全局敏感性系数，见图4.

图4 分析变量对排放测算的一阶和全局敏感性系数

由图可知各个参数对排放测算结果的影响差异显著，对于NOx测算模型，运行时间及燃油流量一阶敏感性系数分别达到0.41和0.45，同时注意到与全局敏感性系数相差较大，表明参数间的交互效应对输出产生了较大影响，因此针对交互效应进一步分析得到图5的二阶敏感性系数，NOx的燃油流量-运行时间变量组合的二阶敏感性系数值较高印证了这一推断.图4b)～c)表明对于HC、CO测算模型，运行时间的一阶敏感性系数均大于0.9，而燃油流量、温度和压强敏感性系数小于0.1，因此被识别为非敏感参数.

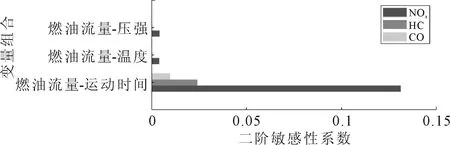
图5 分析变量对排放测算的二阶敏感性系数

综上，针对不同污染物进行测算时，排放模型参数的敏感性具有显著差异，其中燃油流量、运行时间具有较大的不确定性.

4 结 论

1)不确定性分析框架可涵盖模型、参数及观测三方面的不确定性.其中，模型不确定性包括假设分析、模块评估和系统评估的不确定性；参数不确定性主要涵盖LTO边界高度、污染物排放指数、阶段运行时间等关键因素；观测不确定性涵盖测量仪器和方法的使用、周边环境的影响等.

2)表征不确定性的方法通常以概率分布和统计指标为主，并可结合研究实际需求选择诸如模糊数学、非概率区间等其他方法；不确定性量化方法包含泰勒级数、蒙特卡洛模拟、统计分析、敏感性分析等.

3)以广州白云机场为研究对象量化参数不确定性，通过统计分析发现实际滑行时间、爬升时间与标准值之间存在较大偏差；基于蒙特卡洛模拟的污染物排放结果显示，在滑行阶段由于时间及燃油流量的不确定性导致其结果出现偏差；最后针对排放模型进行敏感性分析得出NOx测算偏差受时间和燃油流量影响较大，HC和CO的测算偏差主要来源于运行时间.

未来有关机场航空器污染物排放测算的模型将愈趋复杂，航空器排放测算的可靠程度也会受到挑战，不确定性分析框架及内容仍需不断完善和丰富以期提高测算结果的准确性，为科学制定排放清单、实施有效减排决策提供科学参考.