公交线路停靠时间比例特性及影响因素分析

杨宇航 陈国俊 张抒扬 刘好德 祁 昊

(武汉理工大学交通学院1) 武汉 430063) (交通运输部科学研究院2) 北京 100029)

0 引 言

公交行程时间包括站点停靠时间与站间行驶时间，是涉及到公交规划、运营调度和服务评价的重要参数.在以往研究中，停靠时间与行驶时间的获取方法主要分为三类：人工调查[1-2]、GPS数据换算[3-4]和模型估计[5-6].人工调查方法需要耗费大量人力，且通常可获取的数据样本较少.GPS数据换算方法要求必须准确采集车辆的进出站点时间，对数据质量要求较高；数据缺失、异常以及GPS定位误差(包括进出站的判定机制)，都会影响停靠时间与行驶时间的获取.采用模型估计方法时，通常需以二者的影响因素为基础进行建模，停靠时间的影响因素包括上下车人数、车内拥挤程度、台阶数、时段、天气等[7-9]，行驶时间的影响因素包括行程距离、道路等级、车道数、有无专用道、交叉口间距、交通流状况、驾驶行为、天气等[10-13].由于影响因素的差异性与多样性，以往研究者通常对两者进行独立建模分析，缺乏考虑两者间的相互关系，而且构建的模型多针对单个站点或路段，不适用多站点或长距离的时间预测或估计.

在Tirachini[14]的统计分析中显示城市公交线路的总体停靠时间占行程时间的比例在20%～30%浮动，因此，本文进一步提出假设，城市公交线路运营的停靠时间与行程时间之间存在特定的比例关系，且该比例关系在特定条件下保持稳定.如果成立，基于该比例关系，只需极少量数据(路单数据)即可估计获取特定城市公交线路运营的停靠时间.

文中基于济南市公交智能调度数据，验证公交停靠时间与行程时间之间的比例关系，并分析影响该比例系数的因素，建立相应的数学模型，从而得到城市公交线路停靠时间的简便计算方法.

1 停靠时间比例特性分析

1.1 数据基础

从济南公交智能调度系统中提取各个运营日、各条运营线路、各个运营班次在各站点的停靠时间与各路段(相邻两个站点之间)的行驶时间.样本的采集时间范围为2019年9月(30 d)，公交运营线路为306条，总共包含955 812个运营班次.

1.2 比例系数的统计分析

假定公交站点停靠时间与班次行程时间存在稳定比例关系，即二者满足DT=k×TT.从统计角度，采用过原点(行程时间为0时停靠时间也为0)的线性回归方程对数据样本进行拟合应该具有较好的拟合优度.对全样本班次数据进行回归分析，结果见图1.

图1 线性拟合结果

拟合结果k=0.285，停靠时间总体上约占行程时间的28.5%；拟合R2为0.855，比例模型拟合优度较高，能够基于行程时间解释85.5%的停靠时间变化程度；模型的标准残差分布近似标准正态分布，表明拟合结果具备合理性.因此，对城市公交系统，可以判定停靠时间与总行程时间存在显著地比例关系.

1.3 比例系数的稳定性分析

线性拟合验证了停靠时间与行程时间存在比例关系，还需验证比例系数的稳定性.以运营班次为统计单元，计算停靠时间与行程时间的比例系数k.根据全样本比例系数的分布(见图2)，其集中分布在0.2～0.4(约占92%)，不同班次的停靠时间比例系数存在一定程度波动，直接采用全样本拟合的比例系数去折算班次停靠时间会导致较大的误差.

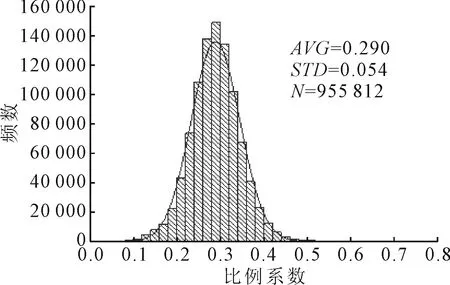
图2 比例系数分布

基于上述分析，可能导致站点停靠时间比例系数波动的原因包括：

1)时段差异 不同时段背景交通流条件不一样，同时客流需求也存在差异.

2)日期差异 类似不同时段，不同日期背景交通流条件与客流需求存在差异.

3)线路差异 不同线路几何拓扑结构不一样，道路行驶环境差异较大，且客流需求也存在差异.

4)驾驶行为差异 不同驾驶员的驾驶行为习惯存在差异.在公交运营当中，驾驶员与车辆之间通常存在对应关系，本研究采用车辆代表驾驶员.

从比例系数关于不同时段(05:00～23:00)、不同日期(9月份连续30 d)、不同线路(30条具有代表性的不同类型线路，运营班次量均大于1 000)、不同车辆(运营班次量最大的K1线路)的分布来看(见图3)，时段、日期、车辆的差异对比例系数分布的影响程度非常小，不同时段、不同日期、不同车辆的停靠时间比例系数分布近似相同；而线路差异对比例系数分布的影响程度非常大，不同线路的停靠时间比例系数存在着显著差异.

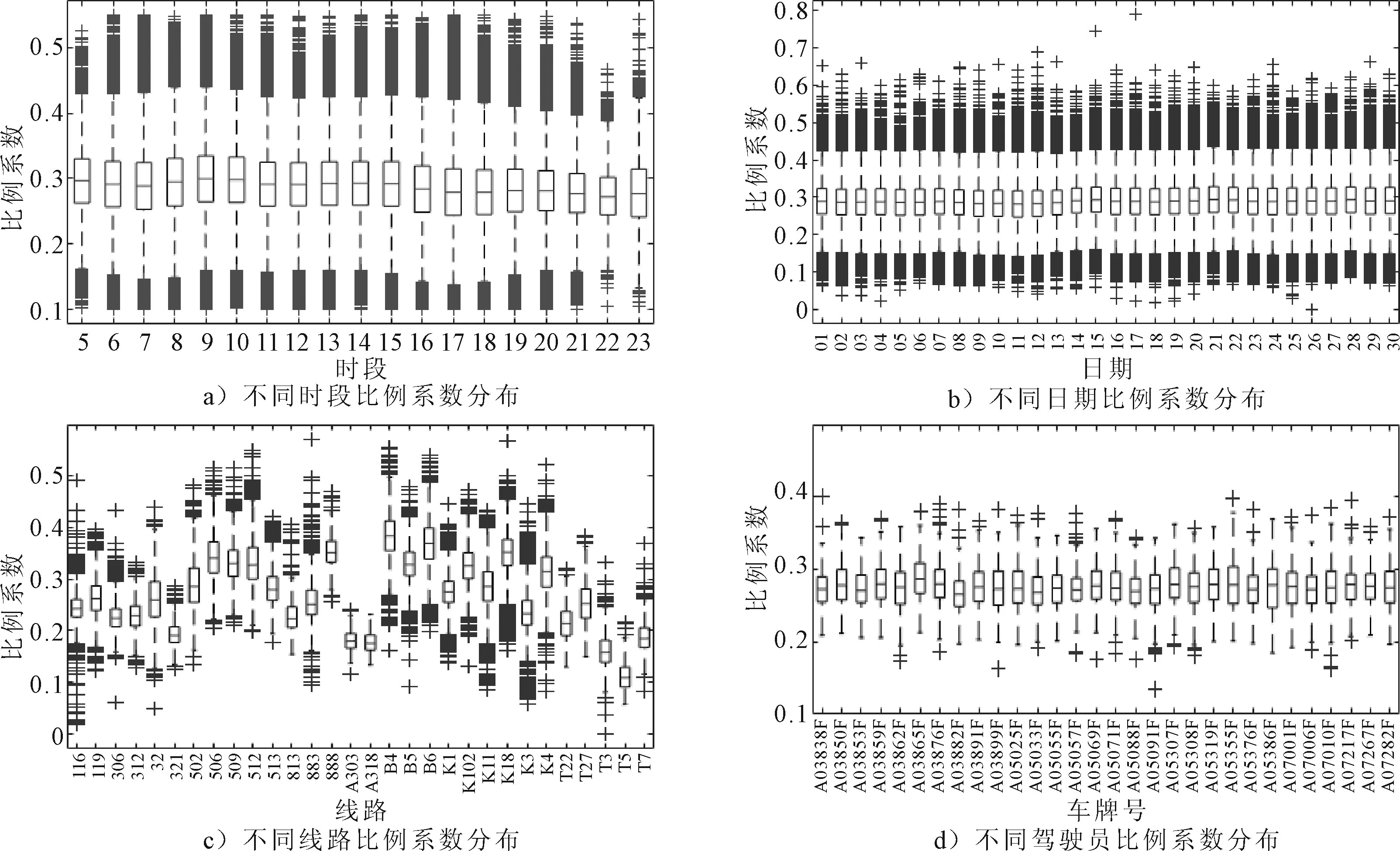
图3 不同条件下比例系数的分布

因此，文中主要从线路空间差异角度分析停靠时间比例系数差异的原因，从而提升停靠时间估计的准确性.

2 线路因素对比例系数的影响

2.1 潜在影响因素分析

在固定行驶路径的情况下，每条公交线路的特征是固定的，背景交通条件具有特定的规律特征；同时文献[15]显示居民的公交需求具有显著的空间特征，因此每条固定线路的客流需求也将具有规律性.不同线路比例系数的分布存在明显差异，为确定影响比例系数的具体因素，需要结合线路差异特征进行分析.

站点停靠时间比例系数取决于站点停靠时间与站间行驶时间，即

(1)

式中：dt为单个站点的停靠时间；lt为单个站间路段的行驶时间.

影响停靠时间比例系数的因素可以概括为两方面，影响站点停靠时间的因素与影响站间行驶时间的因素.

1)站点停靠时间影响因素 对于停靠时间，研究表明其主要影响因素为上下车的乘客数，即：

dtn=μbn

(2)

式中：bn为站点上下车乘客数；μ为单个乘客的平均服务时间.

从线路角度而言，影响停靠时间的潜在因素包括：①线路站点数站点越多，公交车停靠次数越多，停靠时间越长.②线路高需求站点数站点300 m服务半径内有大型居民出行需求点，如居民区、医院、学校、商业区等，定义该类站点为高出行需求站点，这类站点乘客上下车需求较高.

2)站间行驶时间影响因素 行驶时间由行驶距离与平均行驶速度决定，即：

(3)

式中：ltn,n+1为站点n与n+1之间的行驶时间；sn,n+1为站间距离；vn,n+1为站间平均行驶速度.

结合文献[7-10]，从线路角度，影响站间行驶时间的因素包括：①线路长度 线路越长，行驶时间越长.②线路所处道路等级 不同等级道路的设计行车速度不同，速度越快，路段的行驶时间越短.城市道路以主干路为主实现交通功能，故采用线路包含的主干路运营长度反应公交线路所处道路等级状况.③线路是否专有路权 在专有路权道路上，公交车速稳定，路段的行驶时间更短.由于济南市的公交专用道按时段划分，而不同时段比例系数无明显差异(见图3a))，因此不考虑一般的分时段公交专用道，主要考虑是否为BRT线路(全时段公交专用道).④线路交叉口数 交叉口越多，车辆遭遇信号控制次数可能越多，频繁制动导致站间行驶时间越长.

考虑到不同线路的站点数、高需求站点数量、交叉口数、主干路运营长度等参数的绝对值差异很大，不具有可比性.本研究将上述参数转换成线路之间具有可比性的相对值，即站点密度、高需求站点率，交叉口密度、主干路占比.

文中选取的影响停靠时间比例系数的线路因素见表1，并通过百度实景地图采集了运营班次大于1 000的197条公交线路的特征参数.

表1 潜在影响因素

2.2 相关性检验

为确定上述潜在影响因素是否对比例系数存在显著影响.基于SPSS对比例系数与潜在影响因素进行相关性检验，其中连续型变量采用皮尔逊相关系数检验(见表2)，分类变量采用点二列相关系数检验,见表3.

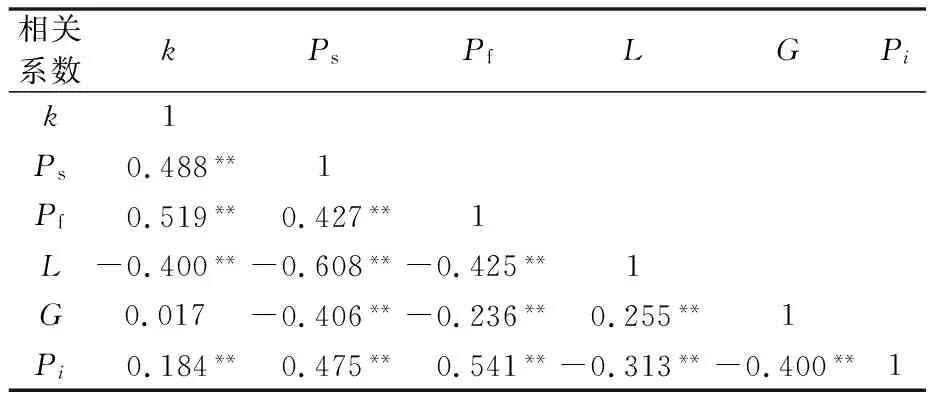
表2 皮尔逊相关系数表

表3 点二列相关系数表

以显著性水平Sig=0.05为相关性筛选阈值，结果发现，站点密度、高需求站点率、线路长度、交叉口密度、是否为BRT线路与停靠时间比例系数(k)之间存在显著相关性，而主干路占比与停靠时间比例系数之间不存在显著相关性.在后续的建模分析中，只考虑站点密度、高需求站点率、线路长度、交叉口密度、是否为BRT线路等五个线路因素与停靠时间比例系数之间的关系.

2.3 回归建模分析

将显著影响因素作为自变量，线路的平均比例系数作为因变量，分别构建多元线性回归模型、BP神经网络回归和随机森林回归模型(使用matlab自带的神经网络和随机森林工具箱)，并比较3种模型的拟合优度(R2)与估计精度(MAPE)，见图4.

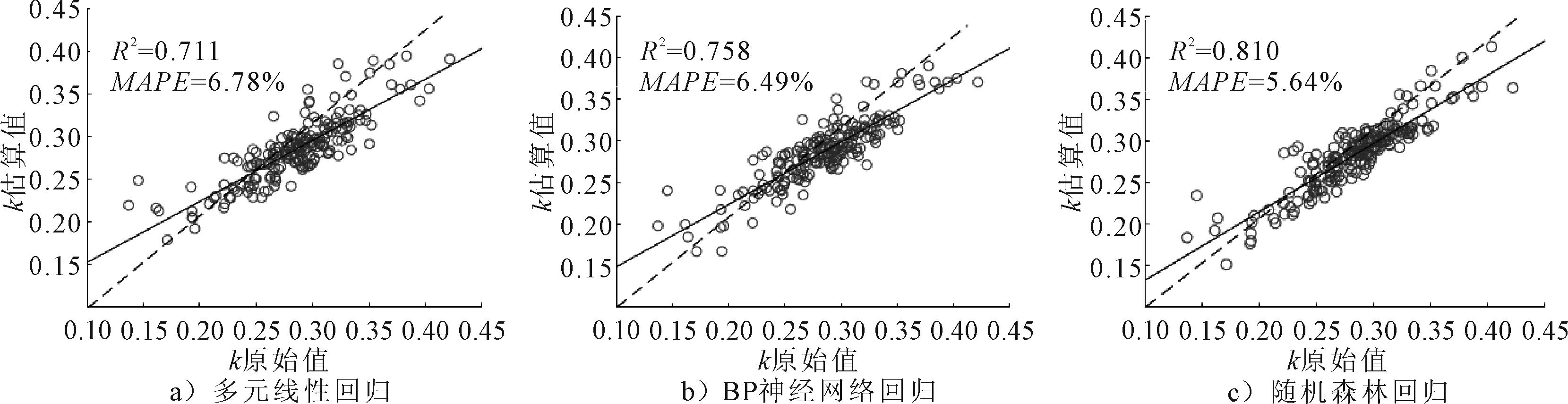
图4 三种模型的拟合效果

根据R2和MAPE，相比多元线性回归模型，其他两种智能算法在精度上均有提升，但改善效果有限，其中BP神经网络模型的MAPE提升了0.29%，随机森林模型的MAPE提升了1.14%.多元线性回归模型虽然精度略低，但是其估计结果仍然可观，说明相比复杂模型，线性回归模型仍对本研究具备有效性；且多元线性回归模型更易于理解与实践，相比其他两种方法便于进行灵敏度分析，能够具体分析各因素的影响程度.因此本文选择多元线性回归模型作为比例系数的估计方法，其模型具体参数见表4.在该模型中，站点密度、交叉口密度、高需求站点率、是否BRT通过显著性检验(Sig<0.05)，对比例系数存在显著影响，且不存在多重共线性(VIF方差膨胀因子<10).

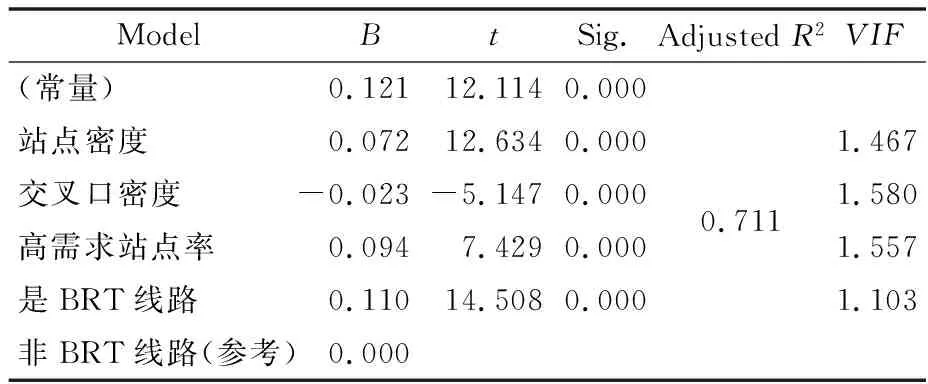
表4 多元线性回归模型

得到多元线性回归方程为

k=0.121+0.072Ps-0.023Pi+

0.094Pf+0.110θ

(4)

为进一步验证上述变量对比例系数的影响作用，比较各变量不同取值情况下线路比例系数的分布，见图5.

图5 各变量不同取值情况下比例系数的分布

1)站点密度 由图5a)可知，随着站点密度的增加，比例系数分布呈上升趋势.站点数量越多，公交运营过程中需要停靠的次数越多，从而导致停靠时间增加与停靠时间占比上升.根据回归方程结果，每公里增加一个站点将导致站点停靠时间比例上升0.072.

2)交叉口密度 由图5b)可知，相比0～1个/km区间，其他两个密度区间的比例系数分布上升明显，这并不符合研究预期.交叉口越多，公交运行过程中在交叉口的延误损失时间越高，从而导致站间行程时间增加与停靠时间占比下降.检验数据后发现，处于0～1个/km交叉口密度的线路数据极少(低于3%)，导致数据的信度不足.比较交叉口密度处于1～2个/km区间与2～3个/km区间，比例系数分布随交叉口密度增加有略微下降.根据回归方程结果，每公里增加一个交叉口将导致站点停靠时间比例下降0.023.

3)高需求站点率 由图5c)可知，随着高需求站点率的增加，比例系数分布明显上升.高需求的站点乘客上下车需求增加，停靠时间增加，导致停靠时间占比增加.根据回归方程结果，高需求站点率每增加1%将导致停靠时间比例上升0.000 94.

4)是否BRT 由图5d)可知，BRT线路的比例系数分布相比非BRT线路有明显上升.BRT线路公交在行驶时不受其他社会车辆的影响，行驶速度稳定，在路段间耗费的行驶时间更少，且通常而言，BRT线路的客流需求高于普通公交线路.因此，停靠时间占比增加.根据回归方程结果，BRT线路相比于非BRT线路，其停靠时间比例增加0.110.

比较197条公交线路的回归模型估计值与相应线路运营班次(878 521个)的比例系数实测值(见图6)，其中相对误差百分比小于10%的累计案例数占比51.6%，相对误差百分比小于20%的累计案例数占比83.5%，全样本的平均相对误差百分比为12.2%，因此，通过公交线路的特征参数计算其停靠时间比例系数，再依据电子表单提供的线路运营班次的总行程时间进行折算，可有效估计所属运营班次的停靠时间.

图6 各运营班次比例系数的相对误差分布

3 结 束 语

本文验证了城市公交停靠时间与行程时间之间的比例关系，并基于该比例特性提出了一种估计城市公交线路运营停靠时间的简易方法.停靠时间比例系数随线路差异而波动，显著影响因素为站点密度、交叉口密度、高需求站点率以及是否为BRT线路，回归模型的MAPE约为6.8%，可有效估计停靠时间比例系数与停靠时间.研究结果对于指导城市公交线路设计与线网规划、低密度数据质量下评价公交运行服务有重要价值与意义.本研究仅基于济南市公交数据，比例特性是否具有更强的普适性(任何一个城市公交系统均成立)，以及比例系数在不同城市之间是否存在差异有待后续进一步研究.