小学高年级学生数学演绎推理能力培养的教学策略

林晶

演绎推理是指从已有的事实（包括定义、公理、定理等）和确定的规则（包括运算的定义、法则、顺序等）出发，按照逻辑推理的法则证明和计算。在解决问题的过程中，演绎推理用于验证结论的正确性，是建構数学、学习数学的重要思想方法。

研究表明：11岁左右是儿童思维发展的关键年龄段。而这个年龄段，学生刚好已步入小学高年级。我们若能在这个阶段，注重对学生进行演绎推理思想的渗透和教学，势必能帮助学生逐步养成有条理、有依据地思考问题的好习惯，具备清晰表述推理过程及结果的能力，为他们将来顺利进行初中数学的演绎推理证明打下坚实基础。

一、巧设问题情境，体验演绎推理的价值

小学高年级的学生正处在由直观思维向抽象逻辑思维逐步过渡的阶段。在教学实践中，我们应结合小学生的年龄特征及思维特点，设置或有趣、或富有挑战性、或具有探究意味的问题情境，激发学生的推理兴趣，引导学生逐步体验演绎推理在解决问题的过程中所起到的价值与作用。

案例1：五年级上册数学“三角形的面积”。我们可以尝试从学生熟悉的生活实际入手，设置如何求红领巾面积这一有趣的活动情境，激发他们的探究兴趣。求红领巾的面积，实际上就是求三角形的面积。有了之前探究平行四边形面积的经验，多数学生猜测：三角形的面积也应该与它的底和高有关。此时，我们可以顺势抛出问题：如何证明这个猜测是否正确呢？一石激起千层浪，学生纷纷行动起来：画一画、剪一剪、拼一拼……有的尝试利用割补法，将三角形转化为已学过的平行四边形，如图1；有的将两个完全一样的三角形拼成一个平行四边形，如图2。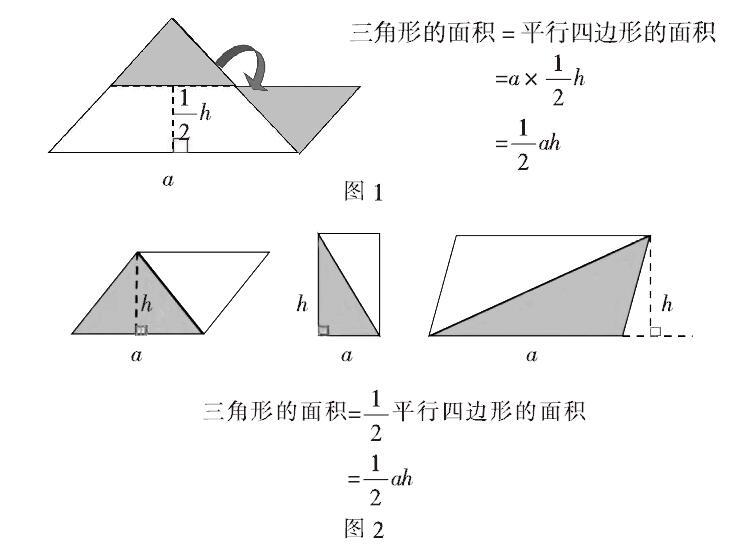

借助上述演绎推理方法，学生体会到：三角形面积的计算方法（新知）可以借助平行四边形面积的计算公式（旧知）来推导。

案例2：五年级下册数学“和的奇偶性”。直接导入课题：研究和的奇偶性，可以先从几个数的和开始研究？学生自然会想到先从两个数的和开始研究。继续设问：两个数的和可以分为几种情况进行研究？答案显而易见：奇数+偶数，奇数+奇数，偶数+偶数。甚至，学生可以借助不完全归纳法列举算式得出结论。如果本节课仅仅止步于此，那么学生的逻辑思维能力并没有得到很好的提升。此时，我们可以尝试引导：像这样的算式永远都举不完，有没有更好的办法，能够帮助我们证明这些猜测都是正确的呢？短暂的沉默后，有的学生提出可以借助奇数、偶数的含义来证明，也有的学生想到了可以用字母来表示奇数和偶数，那么奇数+偶数则可以用2n+1+2n=4n+1表示，即奇数……学生继续研究多个数和的奇偶性，甚至几个数差（积）的奇偶性时，也能借助同样的演绎推理方法解决。

二、优化探究活动，丰富演绎推理的经验

《义务教育数学课程标准（2011年版）》指出：推理应贯穿数学教学的始终。在教学实践中，我们可以根据一节课的教学目标及教学重点和难点，优化探究活动，引领学生在小组合作探讨、操作实践中学会有序、全面地思考问题，于分析推理中体验演绎推理的多种方法，丰富演绎推理的经验。

案例1：四年级上册数学实践活动课“1亿有多大”。为了让学生通过探究活动，经历猜想、实验、推理和对照的过程，利用可想象的素材充分感受1亿有多大，我们尝试以“1亿张纸摞起来有多厚”为研究素材，设计如下实践活动：

（1）启发思考：要想研究1亿张纸摞起来有多厚，真的需要拿出1亿张纸，将它们摞起来进行测量吗？你有什么更好的办法？

学生指出可以先测量一部分纸的厚度，再根据这部分纸和1亿张纸的关系，推算出结果。

（2）学生猜测：1亿张纸摞起来到底有多厚？（20米、50米、100米）

（3）小组实验操作，合作交流。

（4）和实物对照，感受1亿张纸摞起来的高度。

①和学校教学楼的高度比。

教学楼大约20米高，那么1亿张纸摞起来的厚度相当于500栋这样的教学楼的高度。

②和世界第一高峰比高度。

1亿张纸摞起来的厚度比世界第一高峰的高度还要高！

（5）你们还想研究哪些和1亿有关的问题？准备怎么研究？

……

先测量部分量，再由部分量推算出整体。这种推算的过程其实就是演绎推理的过程。借助这样的推算经验，学生便能轻松解决像“1亿粒米有多重”“1亿枚硬币摞起来有多高”等问题。

案例2：六年级下册数学“逻辑推理”。如何让学生在复杂的信息中学会分析、推理，做出准确判断，并感悟解决问题策略的多样化？

（1）出示例题，解读关键信息。

六年级有3个班，每班有2个班长。开班长会议时，每次每班只要1个班长参加。第一次到会的有A、B、C；第二次有B、D、E；第三次有A、E、F。请问：哪两个班长是同班的？

（2）小组合作探究，选择合适的方式记录推理过程及结果。

（3）展示交流。

①文字。

由第一次到会的有A、B、C，得出A可能和D、E、F同班，而第三次到会的有A、E、F，得出A和D同班；同理，由第一次到会的有A、B、C，得出B可能和D、E、F同班，而第二次到会的有B、D、E，得出B和F同班；那么C和E同班。

②列表。

用字母A～F表示六个班长，用1、2、3表示这三次会议。

到会用符号“√”表示，没到会则用符号“×”表示。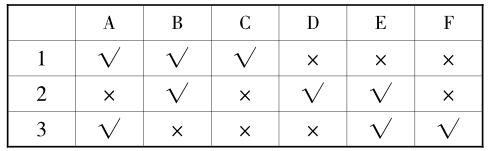

分析得出：A和D同班，B和F同班，C和E同班。

（4）小结提升。

经验1：推理分析的呈现方式虽然不同，但它们都是借助排除法来帮助我们缩小范围，做出正确推理。

经验2：先找关键信息，再确定从谁入手来判断。为什么先确定A与谁同班？（A出现了两次）还可以先确定谁？（B、E）那么C呢？（不行）所以，推理问题时先从信息量大的入手。

经验3：尽量选择直观、简洁的方式呈现推理。

三、强化说理训练，提升演绎推理的能力

在实际教学中，我们常常发现，学生练得多，说得少。课堂中，一遇到“请你说说你是怎样想的，为什么这样想”时，会说并能说清思路的学生寥寥无几。而数学学习，唯有说清数理，方能达到灵活应用、融会贯通的效果。为此，我们需要根据学生的学习难点，有针对性地设计适合说理的习题，强化训练，引导学生学会根据既定的事实、定理证明或推理出新的结论，做到言之有理、落笔有据，从而进一步提升其演绎推理的能力。

“随风潜入夜，润物细无声”。小学生演绎推理能力的形成和提高，是一个长期的、循序渐进的过程。我们既要做好打持久战的准备，又要以落实小学生的数学学科核心素养为根本目标，结合学生的年龄特征和学习特质，制定适合小学高年级学生演绎推理能力发展的培养策略，进一步提高小学生的演绎推理能力。