面向两变量依赖的不等式求解方法

苏本革

（山东省东平县斑鸠店镇中学 山东泰安 271500）

一、引言

当今信息时代中，随着计算机技术的不断发展，新概念不断地提出，数据呈现出了快速增长，而这些大量数据信息中许多是冗余无用的，根据特征来提取所需的知识和信息，用合理的手段来提取数据的特征成为目前所需解决的主要问题。同样的事物具有多种的表现形式，如同一个人的指纹和红热图像。同一句话的不同语言表达，对于相同对象不同的表示被称为多特征数据[1]，即同一个物体的多种特征信息。近年来，多特征数据的研究获得越来越多的关注[2]，因为相比于单特征数据，多特征数据上的研究具有更好的效果[3]。

“维数灾难”[4]是多特征数据经常出现的问题，影响分类识别性能。特征提取和融合成为解决此类问题的关键所在。在同一种模式中，可以通过提取多种特征，来充分体现模式中不同的特点。特征融合的主要目的其一是优化和组合不同的特征实现维数约减，其二是更好地进行模式分类。特征融合主要有以下的优点：首先，不会忽略多特征的有效判别信息；其次，有助于消除特征数据的冗余信息。

串联和整合多种类的特征是特征融合的重要方法之一。其中，特征之间的相互比较采用了特征正则化方法。这种方法在一些范围中有助于识别性能的优化，提高识别率，但是当模式识别时的特征维数极大地增加时，则会有小样本问题[5]出现，使得计算速度相比之前极大地降低。串行特征融合，即基于一个融合矢量的特征融合方法。并行特征融合[6]则是基于复合矢量的特征融合。尽管串行特征融合和并行特征融合都可以有效增强识别能力，却在一定程度上忽略了两个特征集之间的相关关系。这两种方法对于缺乏内在关系两个特征数据集，有效性尚待提高。经过进一步研究，提出了典型相关分析(Canonical Correlation Analysis，CCA)[7，8]，对不同样本的不同特征之间的相关关系进行进一步研究。

典型相关分析是由Hotelling于1936年提出，是一种将两个多维变量之间的线性关系关联起来的方法，CCA利用同一个语义对象的两个视图来提取语义的表示[9]。可以看作是为两组变量寻找基向量[10]的问题，使得变量在这些基向量上的投影之间的相互关系达到最大。随着数据收集和数据存储技术的快速发展，它的理论已经比较完善，计算机的发展解决了典型相关分析在应用中计算方面的困难，成为普遍应用的进行两组变量之间相关性分析技术。

二、土豆、典型相关分析方法（CCA）

（一）CCA优化模型

CCA的准则函数为：

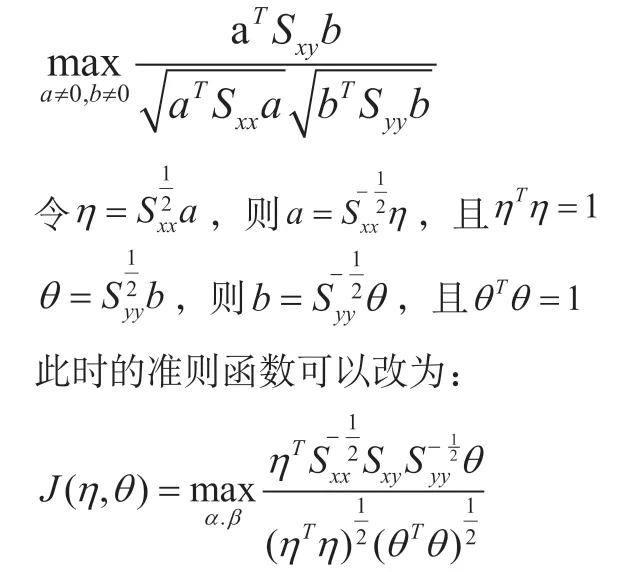
（二）柯西-施瓦茨不等式求解

即：求最大特征值对应的特征向量的方程为：

三、实验与分析

在这一部分中，为了评估所提出的CCA方法，我们在Coil20数据集上进行了一些实验。来验证基于柯西不等式求解的CCA方法对特征融合和识别的能力。

Coil20数据集属于多个对象数据集。其包括20个不同的对象。当物体在转盘上旋转时，每个物体的图像相距5度，因此每个物体具有72个图像。

在Coil20数据集上，每类n（n=15，20，25，30，35）个训练样本，表1展示了CCA方法在Coil20数据集的平均聚类性能。从表中可以看出，CCA拥有较佳的聚类性能。

表1 在Coil20数据集上的实验结果

四、结论

CCA作为经典的两变量依赖分析，是一种用于线性相关特征学习的统计技术，它高度依赖于描述对象的坐标系统。这意味着，尽管数据在不同维度空间上具有很强的线性相关性，但它们之间的关系很难被察觉。CCA可以被看作是为两组数据寻找公共子空间的工具，本文定义了总体典型相关变量及典型相关系数，并详细介绍了利用柯西不等式的求解思路。通过实验与分析我们总结得出，CCA在图像方面的良好聚类性能，并且在模式识别方面已经有了成功的应用和案例，本文在CCA优化求解方面的研究具有重要的理论和实际意义。